适用于任意几何的特征线边界条件处理方法
杨 睿,胡 赟,单浩栋,徐 李
(中国原子能科学研究院 反应堆工程技术研究部,北京 102413)
特征线方法(MOC)具有强大的几何处理能力和天然的可并行性,是实现下一代三维全堆芯高精度、高保真物理计算的优秀方案[1]。当前,直接三维全堆MOC计算程序主要有MPACT3D[2]、OpenMOC3D[3]和APOLLO3中的TDT[4]等。出于减少存储和便于处理边界条件的目的,这些程序均进行了一定程度几何简化,并没有真正适用于任意三维几何。
为向任意几何拓展,需研究任意几何下的边界条件处理问题。当前主流的边界计算方法包括循环特征线法[5]、插值方法[6-7]、打混方法[7]等。在循环特征线法中,特征线能首尾相连,处理简单,不引入边界误差,但只能处理规则几何,对几何有很大限制。插值方法理论上可处理任意几何,但在实践中实现起来较麻烦,另外插值也会引入边界误差。打混方法将边界划分为若干个面,认为每个面上的入射通量是均匀的,计算时将各方向的所有出射通量收集起来进行反射,处理相对简单,但引入误差最多,不仅会引入空间上的模糊,对于曲面也会引入角度的模糊。上述方法均要求为边界条件进行迭代求解,增加了迭代次数。插值和打混方法还要求收集边界通量用于下一次计算,增加了存储要求。
为更好地解决边界条件处理问题,本文提出一种将角通量场拆成源场和边界场分离计算的方法,可同时保留循环特征线方法的连续性和插值方法的几何任意性。
1 特征线方法
离散能群后的稳态中子输运方程可写为:
(1)
其中:φg(Ω,r)为角通量;Σt,g(r)为总截面;Qg(Ω,r)为总角度源;Ω为立体角;r为空间位置;g为能群标号。
反照、反射、周期等边界条件可写成统一形式:
φg(r0,Ω)=α(r′)φg(r′out,Ω′)
(2)
其中:r0和Ω为入射位置和角度;r′out和Ω′为出射位置和角度;α(r′)为反照率,满足0≤α≤1。式(2)表示某处某角度的入射角通量是另一位置和角度下出射角通量乘以反照率。
取r=r0+sΩ,代入式(1)可得:
Qg(r0,Ω,s)
(3)
其中,s为从r0出发沿Ω方向移动的距离。
截面参数中省去r0,通过常数变易法解得特征线方程:
(4)
式(4)中截面与空间有关,源项与空间和角度有关,需进行相关处理。
1.1 空间和角度处理
类似于SN方法,取求积组为角度{Ωm}和求积系数{ωm},每个角度的角通量均满足式(4),角度矩的计算使用数值积分表示;认为空间中材料是由若干等材料区域组成,等材料区域内截面不变;将等材料区域中源项的空间变量以0阶基函数(平源)展开。经上述处理,在每个平源近似区F中的式(4)变为:
(5)
其中,m为角度的标号。
平角度源项可写为:
(6)

(7)
其中:VF为体积;M为总的离散角度数。
1.2 空间矩计算和源更新
(8)


图1 空间矩积分Fig.1 Integration of space moment
大部分特征线方法空间矩中的积分计算使用了控制容积法,本文使用数值积分法,将式(8)中的面积分离散为若干个点来求解积分,即:
(9)
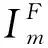
(10)
代入式(8)和(9)中可得到:
(11)
如果近似认为:
(12)
其中,Δsm为射线密度。则式(12)与控制容积法得到的结果是一致的。数值积分法可避免讨论由于边界不一致引入的误差,式(11)的代数精度为0阶,误差由积分的一阶项决定。
如果各方向的射线密度相同,可近似取:
(13)
其中,LF为各方向的总长度,与角度无关。
实际上对于任意三维几何,由于不能使用循环特征线,所以任意方向的射线密度可以也应当取为相同。通过式(11)可对式(6)进行更新。在源迭代中,源更新的同时还需进行keff的更新,和一般迭代相同,使用:
(14)
式(6)和(14)组成的源更新在每次内迭代计算完成后进行。
2 边界分离计算
内迭代处理的是边界条件(式(2))和特征线方程式(式(4))联立的方程,式(4)的计算可通过平源近似(式(5))处理,还需要解决的是边界条件。
2.1 源和边界分离
将式(4)分解为来自源项和边界的两部分:
(15)
其中:
(16)
(17)
(18)
(19)

(20)
其中,n(σ)为σ上方向向外的法向量。
(21)
又0≤α(r(s))≤1,故:
(22)
式(22)和(20)矛盾,故不存在齐次(无源)方程成立的解,所以边界计算有唯一解,它由源场决定。下面求解这个解。首先考虑源场仅在某处和某角度有出射角通量,其他位置为0:
(23)

图2 边界追踪示意图Fig.2 Boundary tracking diagram
在追踪过程中自动满足了反射边界式(2)和(17),而小于最小角通量后的追踪可近似看作是0解,也成立,所以它是1组可行解,所产生的分布即为式(23)的解。由于反照率小于等于1,且式(17)只会发生衰减,所以整个边界追踪中角通量一直都在缩小,故必然可在有限长度下完成计算。
对于任意源场产生的边界分布可写为:
(24)
其中,δ为δ函数。
容易知道式(17)和(18)的对真空出射通量具有线性叠加性,所以边界场为每个源场出射通量经过边界追踪后的结果的叠加。

图3 分离算法的解释Fig.3 Explanation of separation algorithm
这里对分离算法做一解释,如图3所示,黄色为计算区域,上侧和右侧为反射边界条件。它实际可等效为1个通过翻转生成的4个原图形的组合,翻转时的方向如箭头所示。对于从真空边界出发到达另一真空边界的绿→蓝→红射线,它等效于绿虚线→蓝虚线→红线。特征线方程类似于积分输运方程,都使用了首次碰撞的思想,中子生成后一旦发生包括散射在内的首次碰撞就认为消失。这样绿虚线上生成的中子只会按原方向沿蓝虚线、红线组成的射线向前运动,运动时只会发生衰减,即绿线(源场)中生成中子,在蓝、红线(边界场)中衰减。同样,蓝虚线上也会生成中子,在红线中衰减。绿虚线、蓝虚线和它们的后续追踪,加上红线部分就构成了整条线上的角通量分布,也即分离计算的流程。
在实际计算时,认为源场产生的边界分布的离散方式与内部追踪的离散方式一致。这样源场中的1条射线追踪完成后,可不进行下一条源场射线追踪,而是接着进行边界场中的追踪。源场和边界场的射线可实现完全的首尾相连,不需进行插值方法的复杂处理。同时由于边界场天然有限,不要求和循环特征线一样返回原点,解除了几何限制。
2.2 空间矩计算

图4 反射段无法和已有段对齐示意图Fig.4 Scheme of unmatched reflective segment

为此通过插值方法计算该段的角度和空间求积系数。先进行角度插值,由于绝大多数求积组的方位角是均匀分布的,故每一极角层中各方位角的权重一致。假设Ω的极角余弦为μ,它介于μn和μn+1两层之间,每层求积系数分别是ωn和ωn+1,则可取:
μn<μ<μn+1
(25)
其中,φ为方位角。空间求积系数的计算为:
(26)
角度的空间求积系数w(μn,φi)按式(10)计算。若各方向射线密度相同,利用式(13),则各方向空间求积系数相同,不需要计算式(26)。
权重计算完成后,空间矩计算可写为:
(27)
2.3 迭代计算流程
迭代计算流程如图5所示。这里虽保留了内迭代的说法,但内迭代实际只是角度、真空射线、能群的循环,不存在迭代。
在实际实现时,源场中射线各段信息是按照预先设定的射线密度提前追踪完成。但反射场中的射线由于开始时并不知道要追踪多长,因此采用了一种“需要时生成并保存”的方式(图5中虚线框)。当射线到达边界且出射通量没有达到最小通量时,那么检测反射射线是否已生成,若未生成,生成并保存;若已生成,则沿着先前保存的射线信息计算。另外,由于权重计算只与角度有关而与具体追踪过程无关,且计算成本很小,可以在发生反照或反射时进行计算。
每条源场射线的初始通量为0,先按式(16)进行有源计算,然后通过边界处理式(2)后开始边界追踪。虚线框下的通量过小判断实际是在计算式(17)的同时进行,对于式(17)中的每一段均会检测,如果出现通量小于限定值则进入下一源场射线追踪。如果该边界线追踪完成后还没有过小则继续追踪下一条边界线。因为边界追踪是持续衰减的,所以经过有限长度后必然可以小于给出的限定值。

图5 迭代计算示意图Fig.5 Scheme of iteration calculation
边界分离计算是指源场射线和它的反射射线采用有源和无源两种方法,是计算方法的分离,但几何和通量传递上是连续的。与循环特征线方法相比,这种方法相当于一种长度有限的循环特征线方法,特征线首尾相连。但由于边界自然衰减至0,并不要求特征线需经过若干次反射回归原点,避免了繁琐的讨论及几何限制。相比于插值方法,该方法相当于将边界上的空间角度插值转移到角度权重插值,而特征线中的求积组又是固定的,插值简单且一次性。
此外该方法还有两个优点:1) 单次特征线循环就可保证边界条件收敛,不需存储边界出射角通量,也不需边界迭代;2) 每条特征线均是独立计算,与其他特征线的角通量无关,初始和结束都为0,不需保存或传递中间通量,便于实现特征线并行计算。
3 数值验证
3.1 Takeda算例
采用Takeda算例[8]的问题1验证本文方法的正确性。Takeda算例是1个三维简化堆芯模型,几何布置如图6所示。

图6 Takeda算例问题1几何模型Fig.6 Calculation geometry of Takeda problem 1
图6中x=0、y=0和z=0平面为反射边界条件,其余为真空边界条件;能群数为2。case1中红色部分填充材料为空块,case2中红色部分填充材料为控制棒。
计算时的参数选择为:网格尺寸取为0.5 cm,射线密度取为0.05 cm×0.05 cm,求积组选择勒让德-切比雪夫求积组,8极角和16方位角。keff计算结果列于表1,循环特征线的计算结果来自MPACT3D[2]。由表1可看出,keff计算结果误差很小。比较了3种材料中各能群平均通量的误差,结果列于表2。

表1 keff计算结果Table 1 Calculation result of keff

表2 平均通量误差的计算结果Table 2 Calculation result of error of average flux
由表2可看出,大部分区域计算结果与参考解的误差总体很小。然而无论是case1还是case2,空块和反射层中第2群的计算结果的误差均较大。这一问题同样在MPACT3D中出现,初步分析主要原因可能是低阶散射带来的影响。为排除这一因素,使用相同截面单独与MAPCT3D的结果进行对比,结果列于表3。由表3可看出,循环特征线方法与边界分离计算的平均通量结果相差很小,均在0.5%以内。

表3 与循环特征线通量结果对比Table 3 Flux comparison with cyclic characteristics method
3.2 C5G7算例
本文方法可用于1/8、1/6或1/12对称的堆芯。以C5G7-2D算例[9]为例,在上、下表面设置反射边界条件以构成三维算例。根据对称性,该问题是1/8对称,取分界面如图7a对角线所示,每个组件均会被一分为二,存在半栅元(图7b)。该分界面被设置为全反射边界条件。
分别计算了没有分界面的1/4堆芯和有分界面的1/8堆芯,栅元内的网格划分为两环和8个扇区,计算结果列于表4。由表4可见,1/4和1/8堆芯的计算结果相差很小,但1/8堆芯可节约48.27%的时间。此类问题需将组件和栅元进行切割,在常规确定论计算中较少见,借助于边界分离算法可进行求解。

图7 1/8的C5G7问题Fig.7 Eighth C5G7 problem
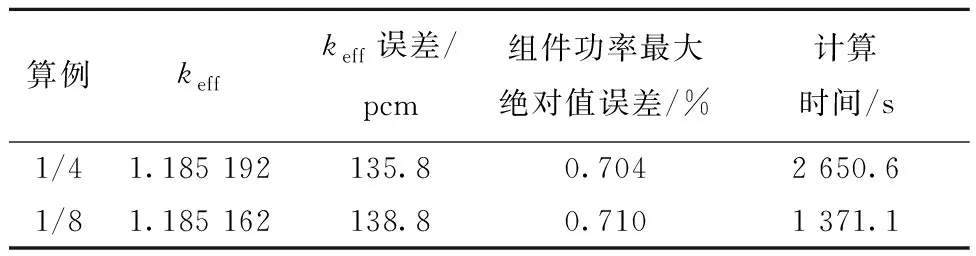
表4 C5G7问题计算结果Table 4 Calculation result of C5G7 problem
3.3 单铀球水腔模型
为进一步验证边界的任意性,采用文献[10]中单铀球水腔模型进行验证。该问题的最外层为球形反射边界条件,内部为轻水,外部为燃料U-10Zr,模型构型如图8所示。
因文献[10]中未给出具体温度,这里温度取为297 K,U-10Zr的密度取为15.92 g/cm3。利用Scale程序进行并群,表5列出MOC程序和Scale程序的计算结果。
计算时采用了0阶散射,对于这种各向异性较强的问题,从计算结果看误差相对于前两个算例较大,但仍在可接受范围内。

图8 单铀球水腔模型构型Fig.8 Profile of single uranium sphere model with water cavity

表5 单铀球水腔模型的keff计算结果Table 5 keff calculation result of single uranium sphere model with water cavity
4 结论
本文提出了一种适用于任意几何的特征线边界计算方法,将角通量场分离成源场和边界场处理,基于数值积分和权重插值给出了迭代计算流程,兼具了插值方法的几何适应性和循环特征线的首尾相连性。经Takeda算例、单铀球水腔模型和C5G7算例验证,与参考解keff的最大误差分别为21、319和138.8 pcm,表明在多种边界条件下计算结果仍然可靠。在该方法下,边界严格对齐且不需存储边界通量,避免了边界条件的迭代;每条特征线可完全孤立计算,适用于特征线并行计算。后续正在开发全堆任意几何的特征线并行计算程序。

