超级均匀化方法在压水堆堆芯Pin-by-pin计算中的应用与研究

张 斌，李云召，吴宏春，王冬勇，刘 勇，于颖锐

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

20世纪70年代以后，得益于粗网节块法[1-2]的迅速发展，以组件均匀化理论[3-4]和粗网节块方法为理论框架的两步法计算方案逐渐成为压水堆工程计算中普遍采用的燃料管理中子学数值计算方法。伴随着粗网节块法的大量工程应用，适用于组件均匀化的均匀化理论得到了长足的发展。基于均匀化一般原理[5]，结合早期有限差分堆芯计算的传统均匀化方法，Smith基于等效均匀化理论提出了能用于工程计算的广义等效均匀化方法[6-7]，即在等效均匀化参数中引入不连续因子以达到各节块的守恒条件，此方法很好地满足了绝大部分商用压水堆的工程应用需求。

随着科学研究的不断深入以及计算条件和对核设计计算精度要求的不断提高，传统的两步法计算方案面临着越来越严峻的挑战。为提高堆芯设计计算精度且满足对新型反应堆堆芯计算的精度要求，基于均匀化理论的改进型两步法计算方案全堆芯Pin-by-pin计算[8]成为下一代堆芯数值计算方法的研究热点。全堆芯Pin-by-pin计算减少了堆芯计算过程中的近似与假设，能更加精细地考虑堆芯布置的非均匀性，直接求出单棒功率分布，便于堆芯燃料管理计算和相应的堆芯安全分析。

有别于不连续因子在传统组件均匀化计算中的广泛应用，压水堆堆芯Pin-by-pin均匀化计算中除广义等效均匀化方法外，超级均匀化(SPH)方法亦是其主流的均匀化技术之一。SPH方法由Kavenoky[9]于20世纪80年代提出。Herbet基于均匀化原理中特征值、各能群反应率及中子泄漏率3个守恒关系不断对SPH方法进行完善，最终使其成为Pin-by-pin计算中的主流均匀化方法[10-11]。SPH方法的核心思想是放宽中子泄漏率守恒这一约束条件，通过SPH因子直接调整栅元均匀化截面使得均匀化前后各能群反应率保持守恒。这种方法不需要均匀化少群常数中保存额外的均匀化常数(不连续因子)，在有很大内存需求量的全堆芯Pin-by-pin计算中具有明显优势。近年来，国内外学者对SPH方法在程序实现、能谱干涉修正、中子泄漏效应处理等方面进行了大量研究[12-19]，日本AEGIS/SCOPE2、德国DYN3D等程序已采用SPH方法作为其Pin-by-pin计算的均匀化方法。SPH方法不受具体堆芯计算模型限制，既可保证均匀化前后输运-扩散守恒，也可保证输运-输运守恒，对于不同的均匀化过程体现在SPH因子修正少群常数时的不同，是压水堆堆芯Pin-by-pin计算中首选的均匀化技术之一。

本文采用SPH方法计算燃料组件的Pin-by-pin等效均匀化参数，针对存在中子泄漏现象的反射层参数计算研究与空间泄漏相关的SPH方法。在保证反应率守恒的基础上，同时保证各栅元各能群的中子泄漏率守恒，解决存在中子泄漏时SPH因子迭代计算的不收敛问题，并分析压水堆堆芯Pin-by-pin计算中应用SPH因子的堆芯计算精度。

1 方法

1.1 SPH方法

均匀化少群截面的计算通常采用通量体积权重方法，如式(1)所示。

x=a,f,s,…

(1)

式中：g、h为能群编号；i为栅元编号；V为栅元体积；φ为反应堆中子通量密度，cm-2·s-1；Σ为宏观截面，cm-1；上标hom表示均匀化后，het表示均匀化前。

式(1)假设栅格计算得到的非均匀中子通量密度等于均匀中子通量密度。此假设在只有均匀化少群截面与扩散系数作为等效均匀化常数的情况下是不成立的。SPH方法通过调整均匀化少群截面使得式(1)成立。

(2)

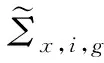
在保证反应率守恒的条件下，有：

(3)

整理可得：

(4)

联立式(2)、(4)可得SPH因子的计算公式：

(5)

式(5)中非均匀栅元平均中子通量密度由栅格高阶输运计算直接获得；均匀栅元平均中子通量密度的求解须与下游堆芯计算中所使用的中子学求解方法保持一致。SPH因子通过均匀栅元平均中子通量密度计算得到，而获得中子通量密度计算所需的均匀化少群常数与扩散系数又需通过SPH因子的修正，因此SPH因子的计算是一反复迭代的计算过程，具体计算步骤如下。

1) 在单组件全反射边界条件下进行高阶输运计算，产生非均匀栅元的平均中子通量密度、各栅元的少群均匀化截面和扩散系数。

2) 初始化SPH因子。

3) 利用SPH因子修正步骤1中产生的少群均匀化截面与扩散系数，并用下游堆芯计算中所使用的中子学求解方法对全反射边界条件下栅元均匀化的组件问题进行计算，产生均匀化栅元的平均中子通量密度。

4) 根据式(5)，利用步骤1、3中的中子通量密度计算结果更新SPH因子。在更新SPH因子前，需对步骤3中产生的平均中子通量密度进行归一化处理，使得整个组件每一能群下的平均中子通量密度与步骤1中的中子通量密度保持一致，归一化公式如下：

(6)

5) 判断SPH因子是否收敛，收敛条件如式(7)所示，若满足上述收敛条件，则计算停止；否则，进入下一次迭代计算，返回步骤3。

(7)

式中，n为迭代次数。

1.2 与空间泄漏相关的SPH方法

在栅格计算中，对单燃料组件采用全反射边界条件进行计算，整个问题在均匀化前后不存在中子泄漏，即利用SPH因子保证反应率守恒的同时还保证了中子泄漏率的守恒，燃料组件特征值也因此而守恒。当SPH方法应用于真空边界，即反射层参数计算时，SPH因子迭代计算的收敛性无法保证。这是因为在真空边界下入射中子流为0的边界条件无法保证出射中子流密度的守恒，迭代过程中改变均匀化少群截面的同时，影响着整个问题的中子泄漏率及其特征值。因此，此类边界条件存在时，SPH因子迭代计算的收敛性无法保证，且在收敛的情况下依旧无法保证整个问题中子泄漏率和特征值的守恒。

针对此类边界下SPH因子的迭代计算，与空间泄漏相关的SPH方法能使迭代计算很好地收敛并保证各栅元中子泄漏率的守恒，其核心思想是以栅元级少群反照率边界条件保证均匀化前后各栅元的中子泄漏率守恒。与空间泄漏相关的SPH方法将栅元级少群反照率的计算更新加入到SPH因子的迭代求解过程中，具体计算流程如下。

1) 真空边界条件下栅格高阶输运计算，产生非均匀栅元的平均中子通量密度、各栅元的少群均匀化截面和扩散系数、组件在真空边界上各栅元的入射和出射中子流密度和少群反照率。反照率计算公式如下：

(8)

式中：βi,g为第i个栅元第g群反照率；h为非均匀输运计算的细群编号；J为中子流密度；角标in、out分别表示入射、出射。

2) 初始化SPH因子并以式(8)计算的栅元级少群反照率作为Pin-by-pin均匀化组件的首次边界条件。

3) 利用SPH因子修正少群均匀化截面与扩散系数，并用下游堆芯计算中所使用的中子学求解方法计算栅元级少群反照率边界下的栅元均匀化组件问题，产生均匀化栅元的平均中子通量密度及边界上各栅元的入射和出射中子流密度。

4) 按照式(6)归一化处理平均中子通量密度，根据式(5)更新SPH因子，迭代过程中真空边界上的栅元级少群反照率的更新如式(9)、(10)所示。

(9)

(10)

5) 判断SPH因子是否收敛，收敛条件为式(7)。若满足上述收敛条件，则计算停止；否则，进入下一次迭代计算，返回步骤3。

与空间泄漏相关的SPH方法通过SPH因子保证各能群各栅元的反应率守恒的同时，通过栅元级少群反照率边界保证各群中子泄漏率的守恒，燃料组件特征值也因此而守恒，计算流程如图1所示。

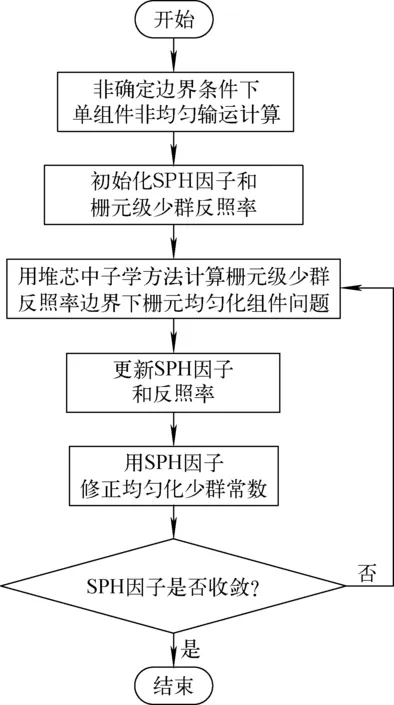
图1 与空间泄漏相关的SPH方法计算流程图Fig.1 Calculation flow of spatial neutron-leakage dependent SPH method

2 数值验证

为验证SPH方法在压水堆堆芯Pin-by-pin计算中的计算精度，以KAIST基准题2A问题下的二维全堆芯问题进行验证与分析，堆芯布置和几何结构如图2所示。

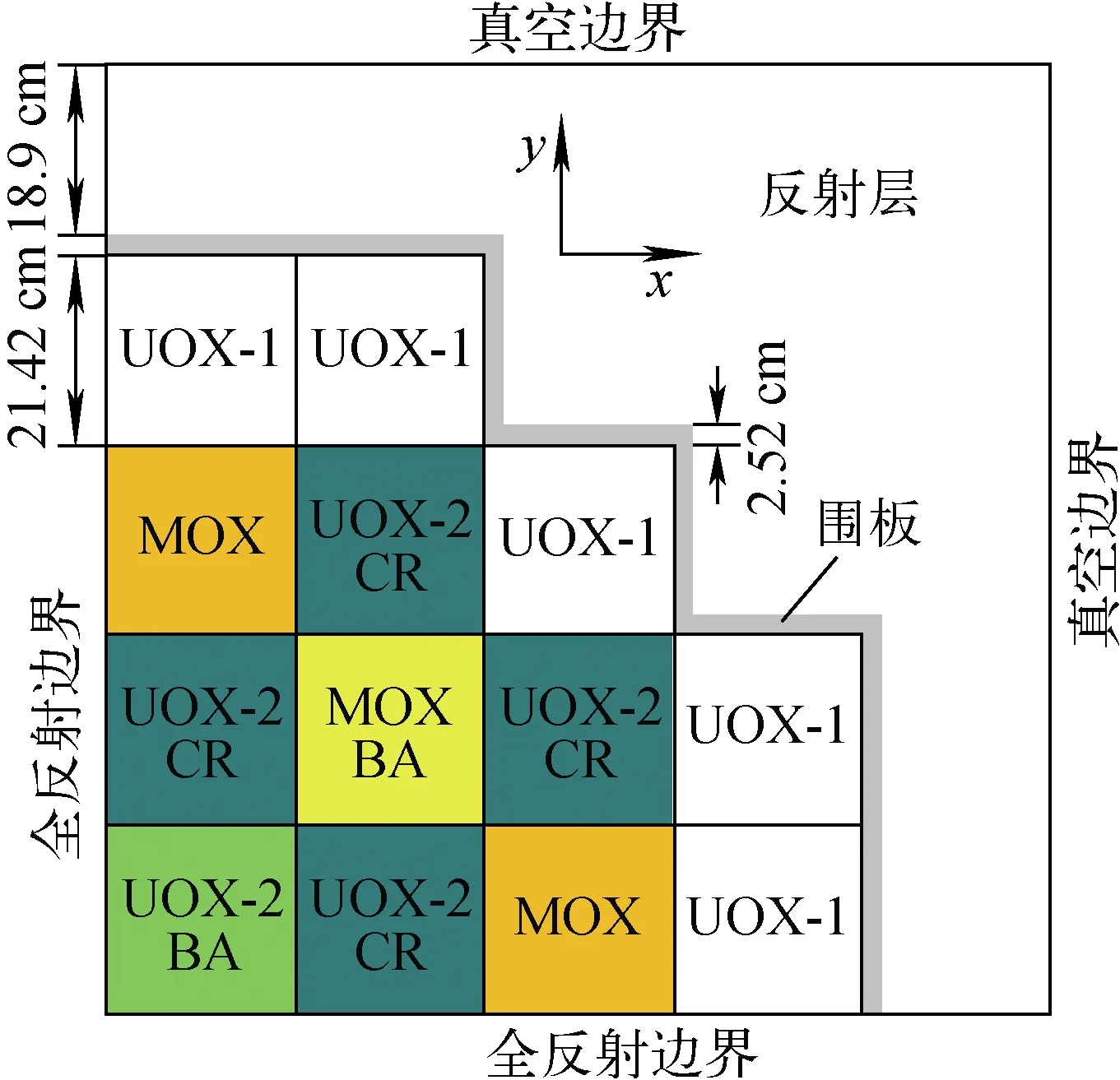
图2 KAIST基准题二维全堆芯布置和几何结构Fig.2 Layout and geometry of KAIST benchmark 2D whole core problem

采用堆芯Pin-by-pin计算和堆芯组件均匀化粗网计算两种方案进行堆芯计算并加以分析和比较。

1) 依据SPH方法及改进型SPH方法的理论模型，针对扩散方法(P1)和简化球谐函数方法(SP3)利用SPH因子分别产生燃料组件及反射层组件的两群和七群的等效均匀化少群常数，并在指数函数展开节块法中进行全堆芯Pin-by-pin计算。

2) 根据传统组件均匀化计算方法，产生两群带组件不连续因子(ADF)的组件等效均匀化常数并采用先进变分节块方法进行堆芯计算。变分节块方法在空间处理上直接针对中子通量密度分布进行离散，因此不需要功率重构过程而能直接得到中子通量密度分布，通过形状因子的求解即可得到堆芯棒功率分布。

二维堆芯参考解由特征线一步法计算获得，特征值参考解为0.979 48，棒功率分布如图3所示。堆芯两步法计算的特征值误差和棒功率误差列于表1。由表1可知：堆芯Pin-by-pin简化球谐函数的计算精度普遍高于组件均匀化的堆芯粗网节块的计算精度；除因误差抵消导致计算精度提高的两群扩散计算外，堆芯Pin-by-pin扩散计算的计算精度均低于组件均匀化的堆芯粗网节块计算。因此，简化球谐函数方法是堆芯Pin-by-pin计算的必要条件；随着能群数的增加，堆芯Pin-by-pin简化球谐函数的计算精度显著提高。七群简化球谐函数计算中特征值误差小于50 pcm，棒功率相对误差的最大值(MAX)低于4%，棒功率相对误差的平均值(AVG)、均方根值(RMS)、平均相对值(MRE)都在1%以下；而在组件均匀化的粗网节块计算中，特征值误差为219 pcm，最大棒功率相对误差接近10%。因此，七群是适用于堆芯Pin-by-pin计算精度的能群数目。

组件均匀化粗网节块计算的棒功率误差分布如图4所示，堆芯Pin-by-pin扩散计算和简化球谐函数计算的棒功率相对误差分布分别如图5、6所示。由图5、6可发现，最大棒功率相对误差出现在组件与组件交界面以及燃料栅元与反射层交界面附近。这是堆芯内组件真实环境与单组件计算中全反射边界条件之间的不同所致。

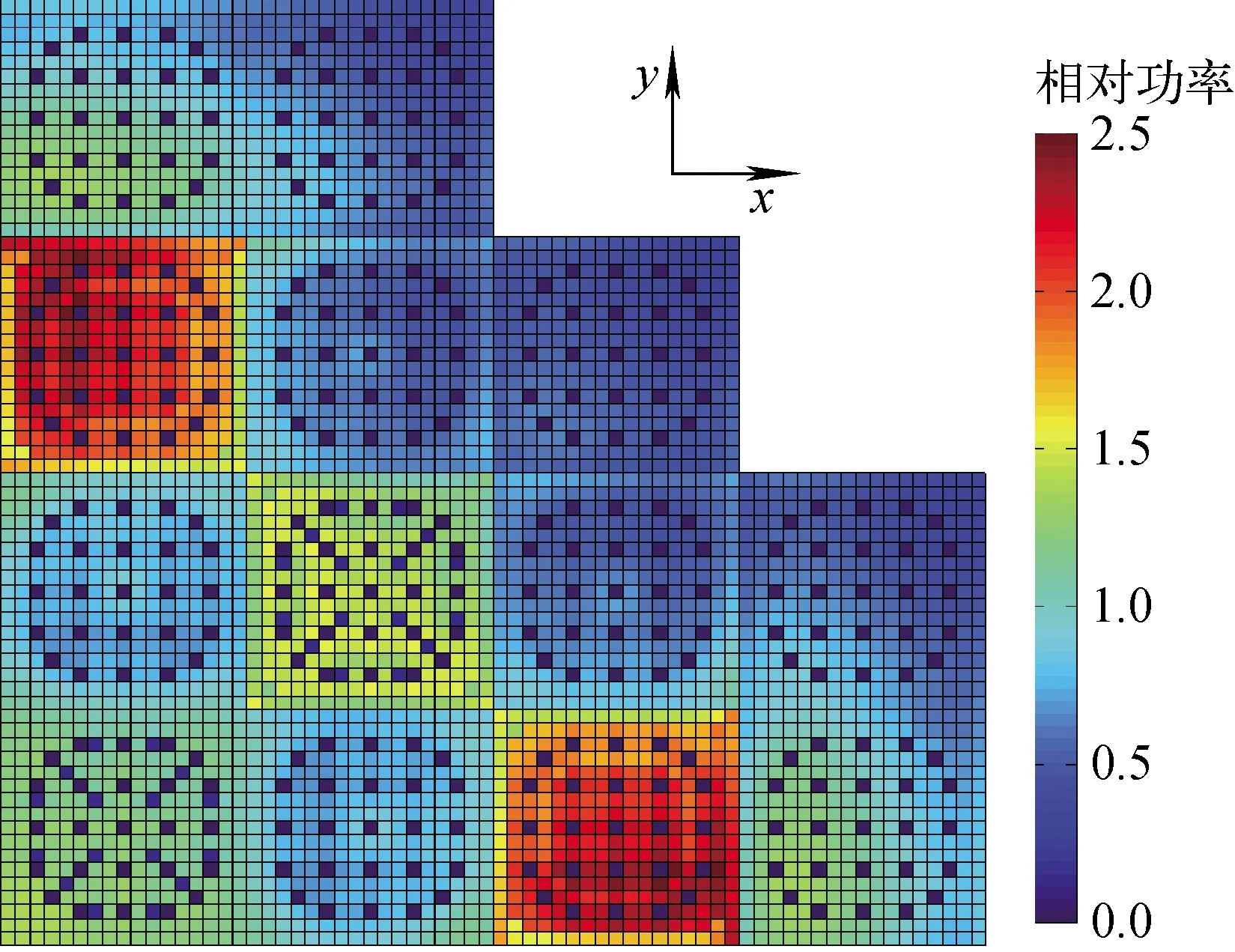
图3 KAIST基准题二维全堆芯棒功率分布Fig.3 Pin-power distribution of KAIST benchmark 2D whole core problem

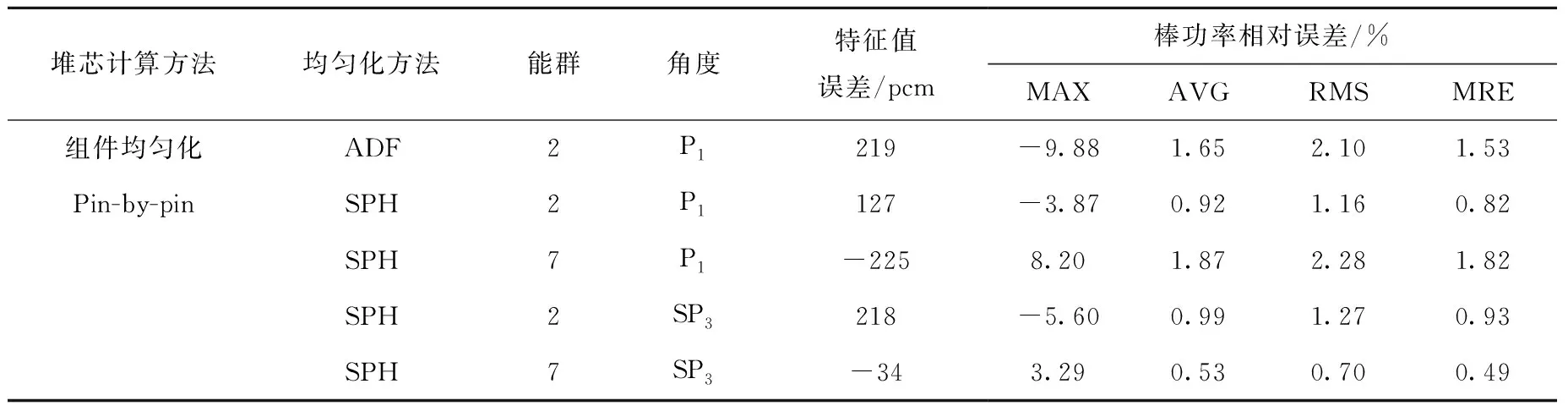
表1 堆芯两步法计算的特征值误差和棒功率相对误差Table 1 Two-step calculation results of kinf and pin-power relative error

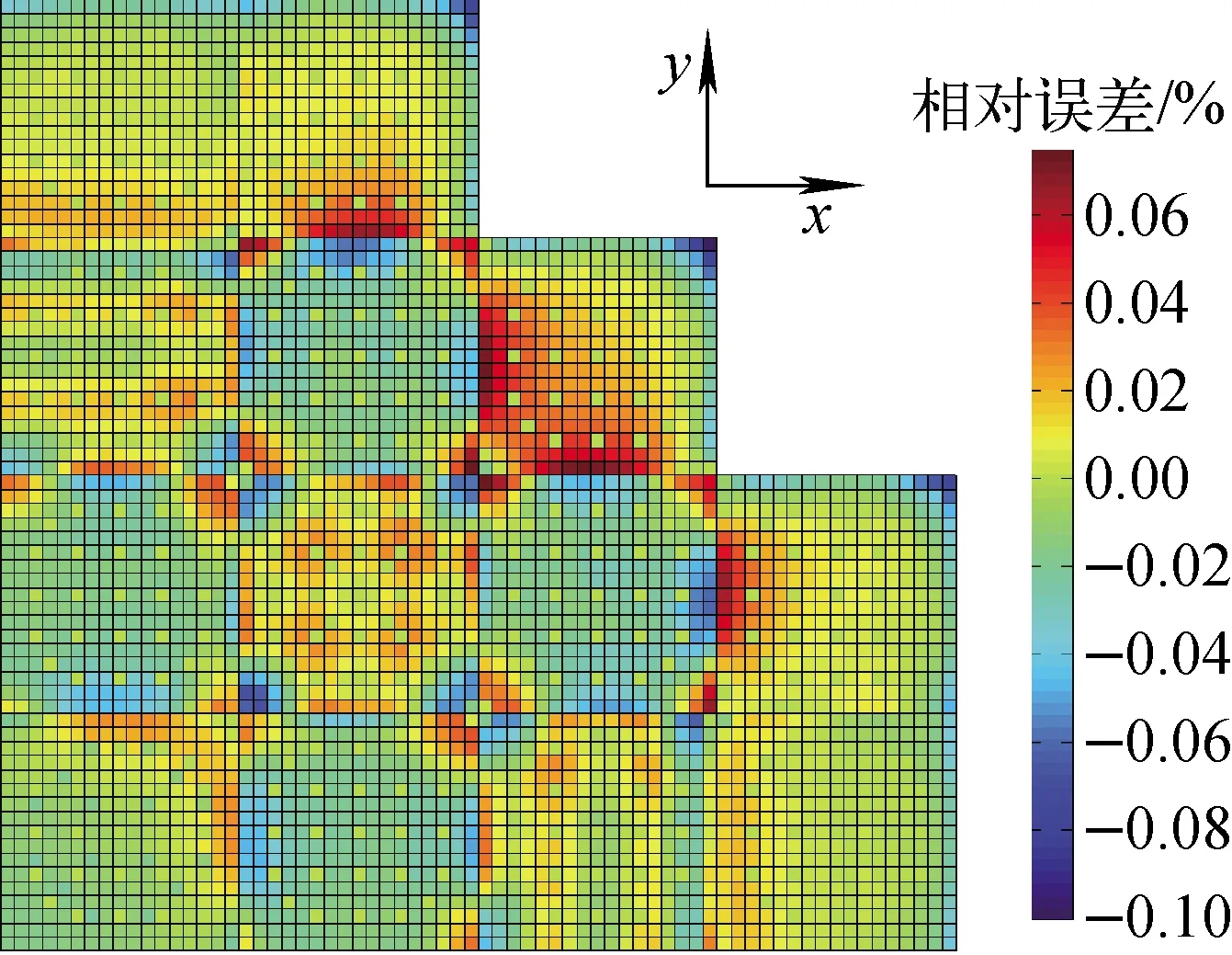
图4 组件均匀化粗网节块计算的棒功率相对误差分布Fig.4 Pin-power relative error distribution of assembly-homogenized nodal calculation

3 结论

本文在压水堆堆芯Pin-by-pin计算中采用SPH方法作为均匀化技术，对燃料组件计算了SPH因子，产生了Pin-by-pin等效均匀化参数；针对存在中子泄漏现象的反射层组件，采用与空间泄漏相关的SPH方法产生了反射层组件的等效均匀化参数。基于KAIST基准题，分析了压水堆堆芯Pin-by-pin计算中应用SPH因子的堆芯计算精度，与传统组件均匀化计算方法相比，应用SPH方法的压水堆堆芯Pin-by-pin的计算精度更高。基于七群的简化球谐函数方法是高精度堆芯Pin-by-pin计算方案的实施策略，与KAIST基准题一步法计算结果相比，其特征值误差小于50 pcm，最大棒功率相对误差小于4%，棒功率相对误差的AVG、MRS、MRE都在1%以下。

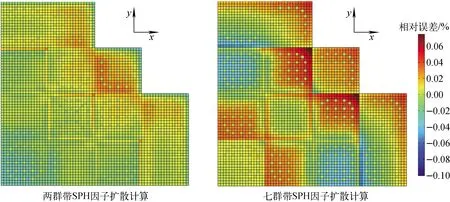
图5 堆芯Pin-by-pin扩散计算的棒功率相对误差分布Fig.5 Pin-power relative error distribution of Pin-by-pin diffusion calculation

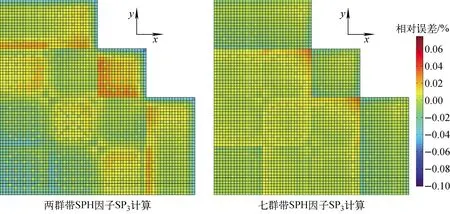
图6 堆芯Pin-by-pin SP3计算的棒功率相对误差分布Fig.6 Pin-power relative error distribution of Pin-by-pin SP3 calculation