三维结构网格SN输运求解的指数短特征线空间离散方法

刘 聪，胡小利，张 斌,*，陈义学

(1.华北电力大学 核科学与工程学院，北京 102206；2.中国核电工程有限公司，北京 100840)

离散纵标法(SN)因其计算效率高、鲁棒性好、适合求解深穿透问题等特点，是核装置屏蔽计算的主要数值方法之一。角度离散误差和空间离散误差共同影响着离散纵标法的数值模拟精度，保证计算可靠性需要控制与问题相关、影响较大的离散误差。在深穿透屏蔽问题中，粒子穿透若干自由程厚的屏蔽层，粒子通量密度的强衰减对空间离散格式的精度与效率提出挑战。基于有限差分方法的空间离散格式尽管其局部截断误差小，但对网格步长较敏感，对于强吸收、粒子平均自由程较短的介质需划分较细网格以保证计算精度。另一方面，差分格式未考虑粒子沿不同离散方向衰减的物理特性，在网格长宽比不佳情况下难以保证粒子传递方向的正确性，引起非物理震荡问题[1]。对于大规模三维深穿透屏蔽问题，一般受计算资源的限制，用户需合理设置计算条件以平衡计算时间和精度。

短特征线离散[2]是一类SN方程空间变量离散方法，该方法根据入射、出射间的贡献关系将计算网格划分为若干子网格，通过与特征线解的空间矩守恒构造出射和网格角通量密度解。Larsen和Alcouffe对一阶空间矩采用差商近似发展了二维线性短特征线离散格式(LC)[3]，Childs和Rhoades利用线性节块SN方程输出近似一阶矩，发展了简化处理的三维LC方法[4]，上述LC方法牺牲了一阶空间矩守恒、忽略了分片物理特性以换取更高的计算速度。自1990年至今，Azmy和Mathews分别基于短特征线离散在二维和三维几何下发展了一系列空间离散格式[5-7]。其中，指数短特征线[8]具有正定性以及出色的粗网格计算精度，对于包含大块屏蔽体的模拟问题具有较高的计算效率。Brennan和Miller利用网格分割、子网格投影变换发展了四面体网格的指数短特征线(EC)格式[9]，Suriano将上述算法扩展至三维笛卡尔网格[10]。子网格投影至标准单位网格的处理过程对于非结构网格求解是不可避免的，但对直角六面体网格而言，相关的几何参数计算可通过适当变换省略简化，以节省用于几何参数计算的时间成本。本文基于三维六面体结构网格推导建立新的EC格式，网格分割后直接计算出射通量矩，以避免将待计算子网格投影至标准单元后再投影回原网格的求解过程，实现对计算流程和参数计算的优化。

1 指数短特征线离散方法

三维几何下m方向的稳态线性玻尔兹曼输运方程如式(1)，即待求解的SN方程。

Σtψm(x,y,z)=Qm(x,y,z)

(1)

式中：ψ为中子角通量密度；Σt为宏观总截面；Q为源强；Ω为方向向量，省略能群符号。

利用方向导数改写式(1)中的泄漏项得到特征线方程，其解沿射线变量s具有以下形式：

(2)

在三维xyz几何下s可表示为式(3)，利用该关系可将式(2)转换至目标网格坐标系下。

(3)

式中：(x0,y0,z0)为射线起点；(x,y,z)为射线终点；μ、η和ξ为方向向量与坐标轴夹角余弦。

考察主象限内某一离散方向，计算网格按入射来源可分为3个子网格(图1a)，每个子网格根据出射面可被细分(图1b)，如此根据出射与入射角通量密度间的贡献关系，计算网格至多被分为7个子网格，每个子网格仅含1个入射面和1个出射面。

a——根据入射面分割；b——根据入射出射贡献关系分割图1 六面体网格分割示意图Fig.1 Hexahedral mesh splitting

1.1 基函数和空间矩定义

在SN求解过程中网格入射条件和源强分布为已知值，由给定初值或上风向网格出射值确定，EC格式假设入射角通量密度和源强为指数函数分布，即：

(4)

式中：i、j和k分别表示x、y、z方向相关参数；a和q为分布系数；b、c、d为对应x、y、z方向的指数因子。

选取变形的勒让德多项式作为基函数，基函数与角通量密度或源强的空间分布进行内积可得到空间矩，见式(5)和(6)。利用空间矩将角通量密度分布在网格之间进行传递，零阶矩为平均角通量密度，一阶矩度量其分布形状。

(5)

(6)

1.2 指数因子求解

目标网格接收3个上风向网格的出射面通量空间矩和本网格源空间矩作为已知条件，需解出其对应分布的指数因子。以网格源矩为例，一阶x矩与3倍零阶矩相除可求解沿x方向指数因子b的非线性方程，即：

(7)

选取其他方向一阶矩可得对应指数因子的待求解方程，求解入射面角通量密度的指数分布与此相同。为方便初值选取，将待求解方程映射至第1象限，求解式(8)得到某方向的指数因子α，根据对称性确定该因子正负。

(8)

式(8)为超越方程，其函数曲线如图2所示，需进行非线性数值求解，指数因子的求解算法需具有优良的精度、效率和鲁棒性。

当α接近0或数值足够大时，可对式(8)进行泰勒展开或分解，选取主导项替代原方程以渐近解直接作为指数因子的值，节省计算量。

(9)

(10)

图2 指数因子求解方程函数图Fig.2 Function of exponential factor solving equation

1.3 角通量空间矩求解

由已知的入射和源强条件，需求解出射面和网格角通量密度分布，即零阶和一阶通量空间矩。从图2可见，使方程f(α)-β=0有解的条件是β<1。通量空间矩的求解涉及若干包含多个指数项叠乘的多重积分计算，积分计算精度不足将导致指数因子求解方程无解，输运计算无法进行。由于指数因子的存在范围广、可正可负，多重积分存在可去奇点等特点，常规计算算法难以满足EC格式要求。本文选用Mathews提出的多重指数矩[9]解决上述问题，其中指数矩定义如下：

(11)

因指数矩M积分上下限特点，在求解出射通量矩时需对图1b的分割方案进行图3所示的细分。

图3 EC出射面通量矩计算分割方案Fig.3 Splitting scheme for EC out-going flux spatial moment calculation

出射面通量矩分别源于边界入射和网格源强贡献，以图1中x方向出射面为例说明推导过程。首先确定子网格范围和粒子来源，利用式(2)和(3)表示出射面上的通量密度分布函数，来源于边界入射和网格源强的零阶空间矩即式(12)和(13)。

(12)

(13)

式中，角标sub-1/2/3、in和Q分别表示子网格编号、入射贡献和源强贡献，总截面角标省略。

变量代换改变积分变量使积分上下限与M指数矩相同，式(12)经变换得式(14)。

(14)

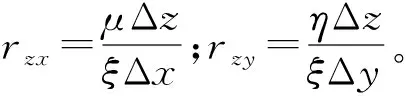
将指数分布假设(式(4))代入改写后的公式，经过适当的合并化简，可将多重积分替换为指数矩函数M，式(12)和(13)最终分别被改写为式(15)和(16)。

M0[ck(1-rzy)]

(15)

(16)

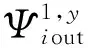
(17)

(18)

参照上述处理过程对y、z方向出射面空间矩进行推导，当某些子网格面积占比极小时取消该子网格计算提高算法稳定性。EC格式是一种非线性空间离散方式，指数矩函数需要在输运扫描中在线计算。指数矩函数计算占据了输运计算大部分的时间，在Mathews和Miller的算法基础上优化了部分参数的计算，合理设置收敛准则提高算法效率。对于网格通量空间矩，采用网格平衡方程(19)和一阶矩平衡方程(20)进行计算。网格空间矩用于更新网格源强，出射面空间矩传递给下风向网格。

(19)

(20)

相比Suriano等的方法，本文建立了新的EC格式，通过对计算网格细分避免进行单元投影映射，无需进行雅可比矩阵和相关向量计算，指数因子求解由耦合非线性方程组问题降为单个非线性方程问题，网格空间矩由矩平衡方程直接给出，降低了计算成本，并对求解算法进行了优化。EC格式具有恒正性同时要求保证非负源，其他求解步骤与标准SN求解相同。

2 基准验证

2.1 空间离散格式计算速度比较

为衡量不同空间离散格式的计算速度，选取“box-in-box”简单几何固定源问题进行模拟。网格划分为25×25×25，采用S8阶求积组。粒子散射的各向异性在实际屏蔽计算中不可忽略，散射源计算的相关开销同样对计算时间有较大影响，因此选取P1、P3和P5阶散射展开进行测试。以P1展开、带置零修正菱形差分(DZ)计算时间为参考，各算例的归一化计算时间列于表1，表中括号内是以相同展开阶数DZ用时为参考的归一化时间。指数定向差分(EDW)[11]是一种基于预估指数分布的差分格式，提高了粗网格精度，但具有差分格式无法正确考虑射线传递过程的共同缺点。ARES输运程序中二维LC格式[12]采用差商近似计算一阶矩，同时引入斜率旋转置零修正，三维LC精确考虑各子网格零阶和一阶矩平衡，根据网格类型预先计算所需的多重积分矩。由表1可见，EC格式的单网格计算成本远高于其他几种格式的。实际屏蔽模拟多采用P3或P5散射展开，随着通量角度矩、散射源计算占用的时间增加，不同空间离散格式用时差距将缩小。EC格式主要用于大块强吸收屏蔽体区域，其较高的单网格计算成本可由其出色的粗网格精度补偿，具体数值分析结果见后文。

表1 简单固定源问题归一化计算时间Table 1 Normalized calculation time of simple fixed-source problem

2.2 Kobayashi基准题

Azmy和Mathews等的研究表明，当短特征线离散用于空腔介质计算时，舍入误差问题可能引起数值精度退化、迭代不稳定。本文EC格式采用矩平衡方程计算网格矩，节省了大量多重积分的计算量，但由于总截面处于分母项，计算空腔介质对求解涉及的参数精度要求较高。经测试发现，采用指数矩函数改写的公式及优化后的参数计算算法具有较高的鲁棒性。选取Kobayashi基准题[13]问题一半散射算例验证EC格式对于含空腔介质问题的精度和稳定性，基准题几何模型示于图4。x、y、z负方向边界为反射边界，其余为真空边界，图中10～50 cm区域材料截面为1.0×10-4cm-1，用于模拟空腔介质，其余区域材料截面为0.1 cm-1，中心0～10 cm区域立方体为源区。

图4 Kobayashi基准题问题1几何模型Fig.4 Sketch of Kobayashi benchmark problem 1

考虑大块真空区域和弱散射介质的存在，该基准题主要用于考验SN程序控制角度离散误差、消除射线效应的能力。为尽可能降低角度离散误差，选取S40阶勒让德切比雪夫求积组，EC格式的关键点计算结果和蒙特卡罗参考基准[14]示于图5，其中1A区域沿直线x=z=5 cm，1B区域沿对角线x=y=z，1C沿直线y=55 cm、z=5 cm。计算结果相对偏差小于±4%，本文的EC格式可正确处理粒子在空腔介质中的输运过程，保证迭代稳定收敛和结果正确。

图5 Kobayashi基准题问题1关键点计算结果Fig.5 Results of key points for Kobayashi benchmark problem 1

2.3 MMS基准问题

(21)

式中:wm为求积组离散方向权重;M为方向总数。

该方法通过调整各边界入射和结合源分布以构造出不同光滑程度的通量密度解。本文设置结合源为阶梯递减分布，构造具有函数连续、指数衰减特征的通量解分布。x、y和z负方向为反射边界，其余为真空边界，模型边长为20 cm，材料总截面为1 cm-1，散射比分别设为0.01、0.1、0.3、0.5和0.7，网格步长设为1 cm和2.5 cm，采用S16阶EON求积组，参考基准分布示于图6。

根据式(22)统计系统标通量密度L2范数误差因子，该因子衡量系统相对误差总和。由于模拟采用的网格步长已超过粒子平均自由程，该基准问题主要考验空间离散在粗网格条件下的计算精度。

(22)

式中：NIJK为网格总数；ΔVijk为网格体积。

误差因子的统计结果示于图7，对于该问题EC和LC格式精度相当且优于其他方法。随着散射比的提高，网格内通量密度衰减减弱，EC和LC的精度优势随之减弱。网格步长从1 cm变为2.5 cm，除SC格式外，其他空间离散格式误差因子均有所上升。由于结合源按阶梯状分布，区域交界处通量密度下降较快，而各区域内部为平源且通量解分布相对平坦，较符合常数特征线SC的基础假设。全局解的非物理振荡问题造成DZ、EDW和θ权重差分TW 3种差分格式的误差因子较大。

图6 MMS基准问题Fig.6 MMS benchmark problem

2.4 平板入射问题

MMS基准问题构造了全局网格的基准解，但由于结合源分布的设置，通量密度衰减速度慢。为模拟屏蔽问题中的深穿透、强衰减特征，通过平板入射问题比较空间离散格式的精度和效率，模型左边界给定常数入射条件，右边界为真空边界，其余边界为反射边界。模型x方向长50 cm，材料总截面为1 cm-1，散射比为0.5，粒子通量密度在系统中将经历超过20个量级的衰减。

比较3种具有较好粗网格精度的空间离散格式EDW、LC和EC，沿x方向25～50 cm间的逐网格通量密度计算结果示于图8，参考解为网格步长为0.05 cm的LC解，图例注明了网格尺寸。当网格步长足够大时需考虑网格内的通量密度变化，EC基于指数分布假设可重构出通量密度分布，图8d展示了EC粗网格下的重构解。

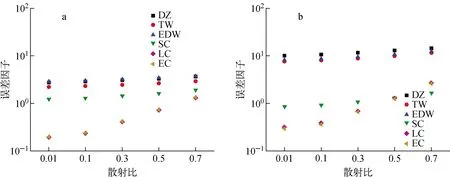
a——网格步长1 cm；b——网格步长2.5 cm图7 MMS基准问题误差因子结果Fig.7 Error factor result of MMS benchmark problem

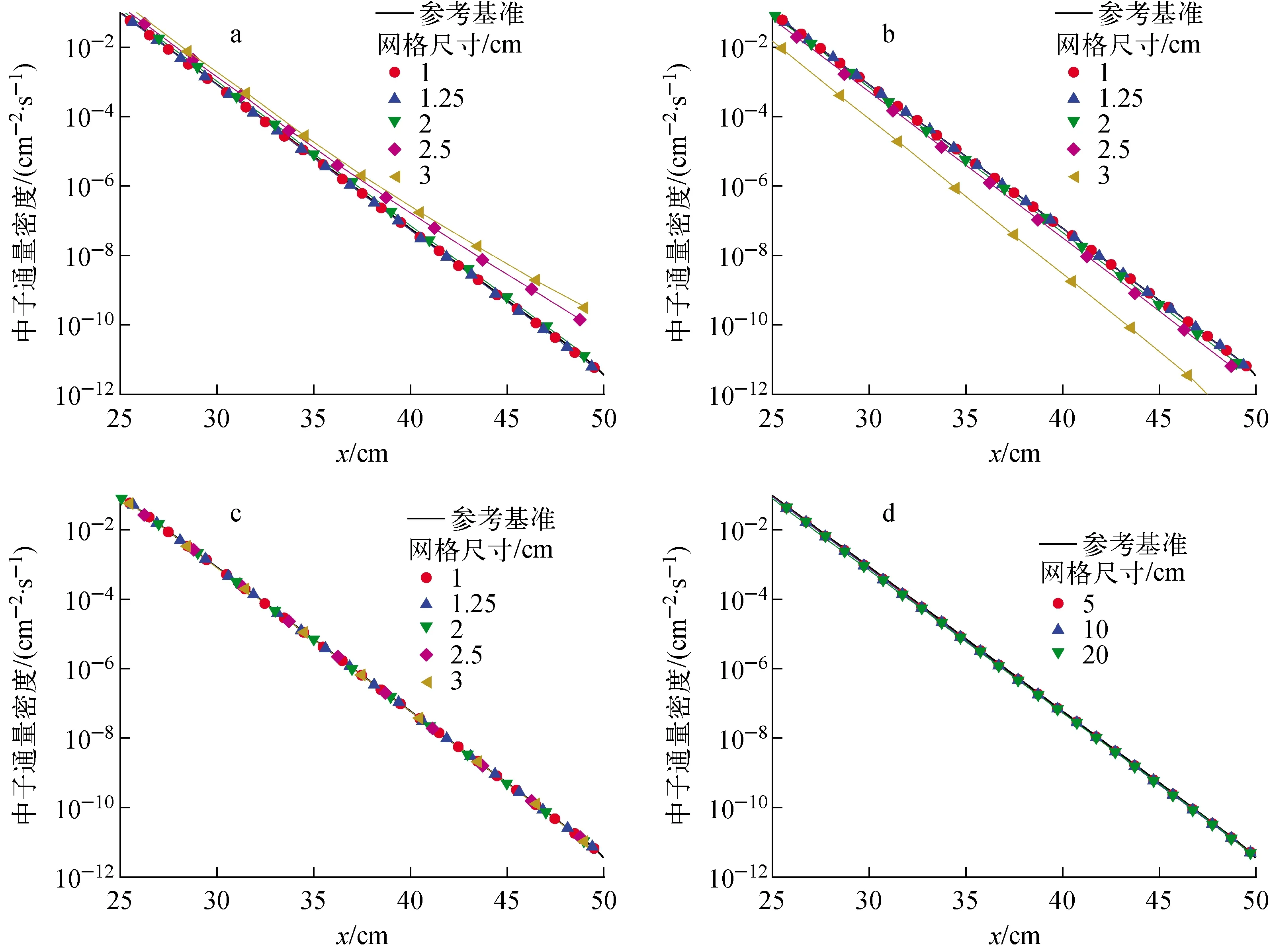
a——EDW结果；b——LC结果；c——EC结果；d——EC重构解结果图8 平板入射问题不同空间离散格式的计算结果Fig.8 Results of plane incident problems under different spatial discretization schemes

对于该问题，LC和EDW在网格2 cm以下时精度相当，随着网格步长继续增大，EDW解趋于保守，LC由于负解的产生将低估粒子通量密度。在测试的全部网格条件下，EC保证了较高的计算精度，当网格步长为20倍自由程时也正确模拟了粒子衰减过程。由细网LC解获得重构位置处的参考值，按式(23)统计了EC重构解的均方根相对偏差列于表2。

(23)

表2 25～50 cm间的EC重构解均方根相对偏差Table 2 RMS relative deviations of EC reconstructed solutions from 25 cm to 50 cm

该平板入射问题由于无分布源存在，粒子通量密度呈现强衰减分布，由表2结果可见，EC在极端粗网条件下也可保证较高计算精度，达到同一精度要求下所需网格数量极大降低。根据本例题EC重构解结果和网格量，达到均方根偏差小于10%的精度水平，考虑在三维几何下，EC格式所需网格数量相比EDW和LC格式将减少约(5/2)3至(20/2)3倍，EC格式较高的单网格计算成本问题可由其所需网格量减少解决，相比带权重差分等粗网格精度不佳的空间离散方法，EC效率优势将更为显著。对于大块厚屏蔽体，EC格式可在较少网格数量条件下达到所需精度。

3 结论

本文基于离散纵标方法提出了新的指数特征线空间离散格式，通过适当的子网格分割和变量代换，避免进行单元投影映射，节省了几何参数计算量，借助指数矩函数保证了算法稳定性，指数因子求解和指数矩函数计算相关算法在已有研究基础上进行了优化改进。通过4个简单几何固定源问题的模拟分析，展现了EC格式出色的粗网格计算精度。综合考虑单网格计算成本和粗网格下的计算精度，EC格式对于实际屏蔽问题的计算成本可接受。对于含有大块均匀屏蔽体的三维深穿透屏蔽问题，相比其他空间离散方法，EC格式达到相同计算精度所需网格量可减少约1～3个量级，在未来自适应空间离散策略研究中EC将作为有力补充。合适的网格划分是发挥EC方法计算能力和效率的前提，网格步长设置过小将极大增加其计算成本，未来将利用间断非匹配网格增强EC对实际复杂几何模型的应用能力。