具有近似仿射尺度不变特征的快速图像匹配

岳 娟，高思莉*，李范鸣，蔡能斌

(1. 中国科学院 上海技术物理研究所 智能红外感知重点实验室，上海 200083；2.上海市现场物证重点试验室，上海 200083)

1 引 言

近些年，随着摄影技术的发展与普及，基于多视角图像匹配的三维数字城市建模、城市规划与安全管理[1-2]以及各应用背景下的场景重构[3]、场景识别[4]正日益发展起来，这对传统图像匹配技术提出了挑战，迫切需要发展大仿射形变图像匹配技术。

目前，大仿射形变图像匹配方法主要可分为三类[5-6]：(1)采用局部特征稳定区域(Maximally Stable Extremal Regions, MSER),Harris-Affine,Hessian-Affine等算法提取原图中具有仿射不变性的区域，进行特征描述与匹配，这类方法不具备完全仿射不变性，对仿射形变大的场景匹配效果不够好[7-8]；(2)首先采用SIFT,MSER等算法对原图进行粗匹配，计算出描述原图间几何形变关系的变换矩阵H；然后基于变换矩阵H，对原图间的几何形变进行纠正，得到一张原始图像的纠正图像；最后对该纠正图像和另一张原始参考图像再次进行SIFT匹配[9]，这类方法匹配效果很大程度上取决于粗匹配结果，但如本文3.1节home场景SIFT匹配结果所示，对于这类大仿射形变场景，往往由于粗匹配点数量过少，不能或不足以准确计算H矩阵，则难以保证最终匹配效果；(3)ASIFT法。ASIFT算法首先采用近似穷举法的思想模拟相机光轴定向参数，对原图进行正仿射变换，分别模拟出两张原图的斜视仿射图像序列空间；然后在斜视仿射图像序列空间中，进行特征提取与SIFT匹配[8]。该方法以时间换空间，模拟出仿射图像序列进行匹配，来提升算法对图像仿射形变的鲁棒性，具有完全仿射不变性。

但是，ASIFT穷举法的思想带来大量的运算量，且对原始图像进行正仿射变换的物理意义不够明显。另外，在一般的应用场景下，ASIFT对大角度纬度上进行更多的经度角采样的现实意义并不大：如倾斜度t=8时，从2.1节仿射成像模型可知，此时纬度θ=cos-1(1/t)=82.82°，相机光轴与物方平面夹角很小，现实应用中一般很少出现这种情况，然而ASIFT算法却依然在该纬度上进行20次经度采样、仿射变换，造成较大的计算资源浪费。学者们在ASIFT算法的基础上，基于倾斜相机各镜头光轴的相对位置关系这一先验知识，进行不同视角影像间的几何畸变纠正[1,10]，以减少仿射变换模拟次数，但仅限于基于倾斜相机的影像匹配这一特殊应用场景。

基于此，本文从逆仿射变换出发，提出一种具有近似仿射尺度不变特征的快速图像匹配算法Fast-AASIFT，进行仿射变形纠正，估计出原图(相机像平面v)对应的正射纠正图像(物方平面u)，然后在正射图像上进行特征点提取、SIFT描述，最后进行SIFT优化匹配。与ASIFT算法相比，该算法具有更清晰的物理意义，且可基于图像信息大幅减少仿射变化次数，能在保证算法抗仿射形变鲁棒性的同时，又有效提高算法效率，具有应用价值，尤其对基于手机等电子设备拍照的场景重构、场景识别等具有重要意义。

2 Fast-AASIFT算法

2.1 图像逆仿射纠正

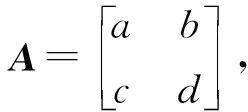
(1)

v=Au.

(2)

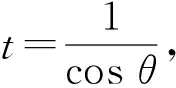
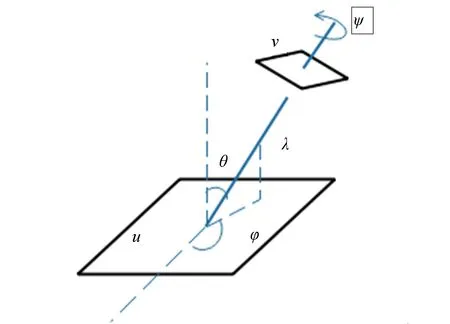
图1 仿射成像模型Fig.1 Affine imaging model

鉴于SIFT算法具有尺度和旋转不变性，可取λ=1,ψ=0，则仿射矩阵A可以简化为：

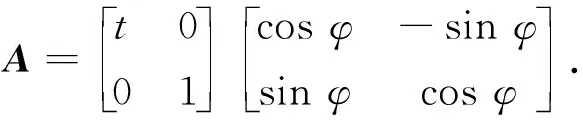
(3)

其逆变换矩阵A-1如下：

(4)

基于式(4)，通过如下2个步骤实现仿射变形纠正，估计出原图对应的正射图像。

2.1.1 尺度变换/倾斜变换

(5)

基于式(5)进行尺度变换，变换过程如图2所示，其中xoy表示像平面坐标系，xIoIyI表示图像坐标系，两者坐标轴单位均为像素(pixel)。记原图I0宽为Wo、高为H0，尺度变换图It宽为Wt、高为Ht，则：

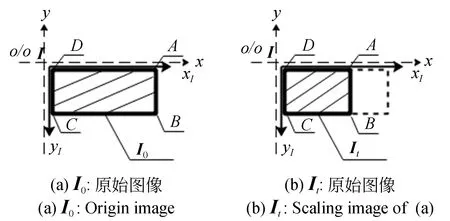
图2 尺度变换Fig.2 Scale transformation

(6)

2.1.2 旋转变换

逆仿射纠正的旋转变换分为以下两步：像平面坐标系下图像逆旋转变换与基于图像坐标系的图像变换。

(1)像平面坐标系下图像逆旋转

如图3(a)所示，基于变换矩阵A-1，尺度图像It绕像平面坐标系xoy的原点，顺时针旋转角度φ，实现逆转换。旋转后图像对应像平面坐标系下的纹理区域Ir。

图3 旋转变换Fig.3 Rotation transformation

记图像的4个角点分别为A,B,C,D，则像平面坐标系上，旋转前It的4个角点坐标分别为：A(xt1,yt1)=(Wt,0)，B(xt2,yt2)=(Wt,-Ht)，C(xt3,yt3)=(0,-Ht)，D(xt4,yt4)=(0,0).

旋转后Ir的4个角点的坐标计算如下：

(7)

即：

(8)

(2)图像坐标系下图像变换

像平面坐标系下的纹理区域Ir最终转换至图像坐标系下，输出图像Ir_out。如图3(b)所示，图像坐标系xIoIyI以左上角为坐标原点，水平向右为x轴正，垂直向下为y轴正，故Ir须经R翻转、T平移才变换至最终纠正图像：

Ir_out=R×Ir+T,

(9)

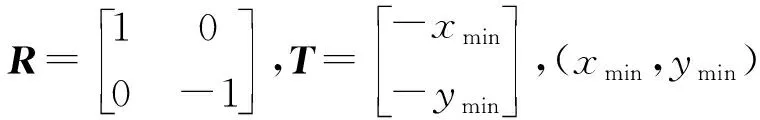
图4 逆旋转示意图Fig.4 Reverse rotation diagram

(10)

记原图I0上像素点P(x,y)，对应纠正图像Ir_out上像素点P′(x′,y′)，P在像平面坐标系下的坐标为(x,-y)，综上有：

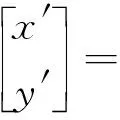
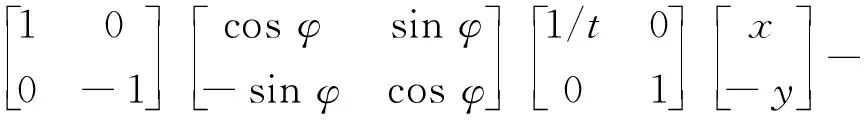
(11)

根据式(11)可推导出：

(12)

综合式(10)～式(12)，本文基于相机仿射形变参数(φ,t)对原图进行逆仿射变换，即可估算其正射图像。在缺少相机先验参数的前提下，虽无法准确获取图像拍摄时的仿射形变参数，但可以结合图1所示仿射成像模型与图像本身信息估计参数(φ,t)取值范围，通过多次模拟变换实现仿射形变纠正。常规拍摄时，相机光轴与物方平面法向量一般会存在一定夹角，即相机纬度，但该纬度不会太大，故可取倾斜度t=[1.1，1.4，1.7，2]，对应相机纬度分别为θ=cos-1(1/t)=[24.6°,44.4°,53.9°,60°]；常规拍摄时，各拍摄位置不会相差太远，结合图1，在各纬度上可取φ=[-20°，-10°，0°，10°]，对相机拍摄位置经纬度参数进行采样模拟，即可实现较好的仿射纠正。

如图5所示为同一手机在不同位置对同一场景(Building)拍摄的两幅原始图像，如前文所述，场景原图不包含相机及拍摄位置等先验参数，但从图像本身可知，两幅场景原图存在较大的仿射形变，但两个拍摄位置相差不远，可以参考前文设置θ与φ，对两幅原图分别进行仿射纠正，得到如图6、图7所示的纠正图像序列。可见在不同的纠正图像中，不同位置处的倾斜的建筑物相继得以纠正：通过不同倾斜度模拟，还原出不同尺度上的场景；通过10°经度模拟，场景中右侧建筑物旋转仿射形变得到较好纠正；通过-10°与-20°的经度模拟，场景中左侧建筑物旋转仿射形变得到较好纠正。

图5 场景原图Fig.5 Origin images

图6 Building1的纠正图像序列Fig.6 Block diagram of image measuring system

图7 Building2的纠正图像序列Fig.7 Block diagram of image measuring system

综上，本文通过16次模拟变换估计出16幅正射图像，用估计出来的正射图像序列模拟出原始图像正射图像的所有特征，实现对原图的仿射形变纠正。

2.2 纠正图像特征提取与匹配

本文按照如下步骤在纠正图像序列上进行SIFT特征提取与匹配[11-16]，该内容相对成熟，不作详细阐述。

(1)在纠正图像上，提取高斯差分(Difference of Gaussian, DoG)特征点并建立SIFT描述子[15]；

(2)进行SIFT特征匹配；

(3)进行基于单应约束及随机抽取一致性约束 (Random Sample Consensus, RANSAC)[16]的匹配优化，参照式(12)将特征点位置反算至原图进行匹配结果输出。本文在对比核线约束+RANSAC优化与单应约束+RANSAC优化两种匹配优化效果的基础上，最终选用后者进行匹配优化，下文将两种优化方法分别简称为核线优化法、单应优化法，并分别用字母F，H进行简易标识。

3 实验与分析

系统环境为Windows10，i5 CPU，8 GB RAM。

3.1 SIFT匹配优化及其局限性分析

3.1.1 SIFT匹配优化

本文在牛津大学计算机视觉实验室图像数据[17]的基础上开展匹配优化研究，并展示其中经典彩色Graf场景与灰色Boat场景的匹配效果图与匹配误差如图8～图9所示。从匹配效果图可见，该场景下两种方法都能匹配一定数量正确同名点。从误差图直观可见，两种方法匹配点数相当，但H法无误匹配点，且匹配精度更高：Graf场景下，F与H法匹配点数分别为31和25，boat场景下，F与H法匹配点数均为21个； 若将匹配误差>5 pixel的匹配点定义为误匹配点，则实验场景下，F法优化后仍存在2～3个误匹配点，而H法优化后无误匹配点；且从局部匹配误差图可见，在其他正确匹配位置上，H法匹配精度整体上优于F法匹配精度。

图8 graf优化匹配结果

图9 Boat优化匹配结果

如式(12)，本文定义优化度C进一步对比两种优化算法效果：

(13)

其中:U1,U2为优化前、后误匹配率，由优化前、后匹配点数N1,N2，以及优化后误匹配点数N3计算而来：

(14)

统计上述实验的优化度如表1所示，可见SIFT匹配算法下， H法优化度>F法优化度。因此，本文在图像匹配阶段采用H法对进行匹配优化。

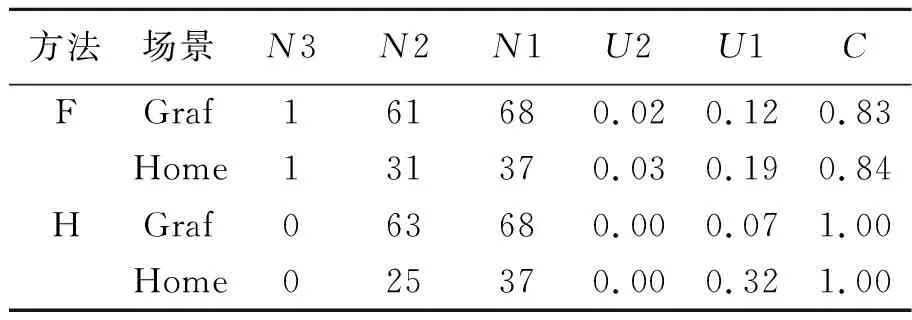
表1 匹配优化结果对比

3.1.2 SIFT匹配算法局限性分析

采用SIFT匹配+单应优化算法对如下仿射形变较大的场景图像进行匹配，其中图10(a)为Building图像匹配优化后结果，优化前后匹配点数分别为11和8；图10(b)为Home图像匹配优化前结果，匹配点数为0。

图10 SIFT匹配结果

可见，在这种仿射变换较大的场景下，SIFT匹配算法正确匹配点数极速下降，尤其当场景特征较少时，正确匹配点数甚至会减少为0，因此，SIFT匹配及其优化算法对大仿射形变场景存在应用局限性，而ASIFT算法以及本文提出的Fast-AASIFT算法正是对其应用局限性进行弥补的算法。

3.2 Fast-AASIF匹配算法实验

在3.1.2节基础上，本节对传统ASIFT算法与本文Fast-AASIFT算法的抗仿射形变性进行对比验证实验。

3.2.1 匹配效果分析

如2.1.2节所述，针对这类常规拍摄场景，本文Fast-AASIFT算法的参数设置为t=[1.1，1.4，7.2]，φ=[-20°,-10°,0°,10°]。如图11和图12所示，分别为两个场景匹配优化的效果图和匹配误差，综合两个场景下SIFT，ASIFT与Fast-AASIFT的匹配结果如表2所示。可见，大仿射形变场景下，相比于单纯的SIFT算法，ASIFT与Fast-AASIFT两种算法匹配点数增加，且匹配误差低：对于Building场景，单纯的SIFT优化匹配算法只能成功匹配到8对优质特征点，然而ASIFT与Fast-AASIFT两种算法能成功匹配到不低于16对的优质特征点；尤其对特征较少的Home场景， SIFT匹配算法已无法正确匹配到特征点对，但ASIFT与Fast-AASIFT算法依然能优质匹配到10对以上特征点。另外，综合两种大仿射形变场景的匹配效果图和匹配误差可见，Fast-AASIFT算法具有与ASIFT算法相当的仿射匹配能力，其峰值匹配误差<2.5 pixel，平均匹配误差<1.2 pixel。

表2 算法匹配误差对比

图11 Building匹配结果Fig.11 Matching results of Building

图12 Home匹配结果Fig.12 Matching results of Home

综上，由于算法对场景图仿射形变进行了有效的模拟补偿，对于实验中仿射形变较大的场景，Fast-AASIFT算法可突破SIFT算法的局限性，实现与ASIFT算法相当的匹配效果，正确匹配到足够数量的匹配点，以服务于后续基于图像匹配的场景重构、识别等应用。

3.2.2 匹配效率分析

匹配算法效率主要体现在特征提取与特征匹配两个阶段上。特征提取、特征匹配的计算量与图像面积、图像面积平方近似成正比[8]。

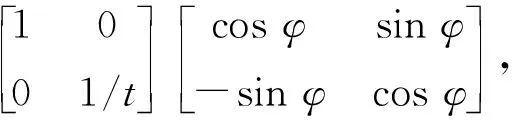
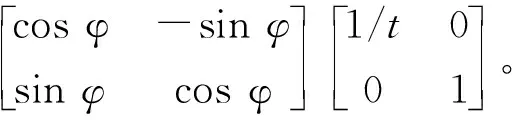
表3 算法耗时对比

4 结 论

针对SIFT等传统匹配算法抗仿射形变能力有限的问题，ASIFT算法以时间换空间，模拟出仿射图像序列进行匹配，来提升算法对图像仿射形变的鲁棒性，但运算量大，且物理意义不够明显。基于此，本文提出了具有近似仿射尺度不变特征的快速图像匹配算法Fast-AASIFT。实验结果证明：大仿射形变场景下，该算法能匹配足够多特征点，且峰值匹配误差<2.5 pixel，平均匹配误差<1.2 pixel，其抗仿射形变能力明显优于SIFT算法，与ASIFT算法相当；该算法耗时<0.3倍ASIFT，大幅改善了ASIFT算法的耗时问题，可见，本文算法既有效保证了算法抗仿射形变鲁棒性，又大幅提高了算法效率，在场景重构、场景识别等领域中具有应用前景。