机载光电平台的对地多目标定位

白冠冰，宋悦铭，左羽佳，王 宣，孙明超

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

作为侦察测量领域的重要工具，机载光电侦察测量设备在航空侦察及民用防护等领域发挥着重要作用。目标定位是通过测量解算得到目标位置信息的过程，是光电平台的一种重要功能。目前机载光电测量设备传统的定位方法是单点定位，即通过飞机导航系统测姿及光电平台的测角和激光测距对侦察区域图像中心十字丝指向的目标进行定位[1-4]。随着多目标检测识别和跟踪等技术的发展，光电平台时常需要对视场中的多个目标同时进行定位。传统的单点定位难以适应光电设备的需求。因此，如何实现光电设备的多目标实时高精度定位成为航空侦察领域的发展方向之一。

为实现光电侦察设备对目标的高精度定位，广大学者对各种定位算法进行了探讨和研究。王宣[5]通过传统定位算法得到主目标的位置信息，以主目标的高度为基准，根据次目标的图像点信息，最终得到多个目标的位置信息，该方法适合于平坦地面的多目标定位，在高度跨度大的区域，定位误差较大。阎明等根据光电平台得到其他目标与主目标的角度关系，结合飞机的高度得到各目标相对平台的距离，从而实现对各目标的定位。Han[6]等提出使用SIFT算法提取出目标在多帧图像下的特征点，通过三维重建完成对目标的定位，该方法需要进行特征点匹配，运算复杂度比较高，难以实现实时定位。Eric J. Stich[7]等提出采用基于WGS-84坐标系的椭球模型对地面目标进行定位。但由于这种方法未考虑到目标区域的高程信息，因此当目标区域的地形起伏很大时会出现较大的定位误差。Farmani[8]等提出一种基于扩展卡尔曼滤波的多目标定位方法，结合动态加权图确定目标密集区域，然后采用模型预测控制算法进行姿态优化，以提高多目标定位精度。

本文分析了各种多目标定位方法的优缺点[9-10]后，结合现在数字地图的广泛应用性，本文提出了一种基于数字高程模型(Digital Elevation Model，DEM)的多目标定位方法，该方法的基本原理如下：首先根据飞机导航系统给出的姿态信息、光电平台的测角信息和目标在图像中的位置信息，可得到多个目标的视轴指向矢量，然后依据DEM信息构建基于目标的椭球模型，得到各目标的位置信息，最终实现对同一视场中多个目标的实时定位。该方法相比现有的多目标定位方法，减小了地面起伏导致的定位误差，可有效提高位置测量精度，且具有更广泛的战场适用性。

2 基本工作原理

多目标定位系统主要由光电平台、飞机导航系统和DEM数据存储单元等部分组成，其中光电平台安装于飞机机头，采用两轴四框架结构，内部有成像载荷，激光测距机，测角编码器等。多目标定位的基本原理如图1所示，在飞机飞行过程中，光电平台在搜索到感兴趣区域后，主目标会被锁定到视场中心区域，此时定位系统采集测角系统输出的俯仰角和方位角，POS输出的飞机姿态和位置，激光测距机输出的距离信息，通过坐标转换运算，得到主目标的地理位置信息。而对于视场中的次目标，通过目标检测模块可得到次目标在视场像面中的图像坐标值(xi，yi)，由此可计算出次目标的目标矢量Li，根据测量得到的角度信息对目标矢量进行坐标转换，结合DEM高程数据和地球椭球模型，可计算得到各个次目标的位置信息。

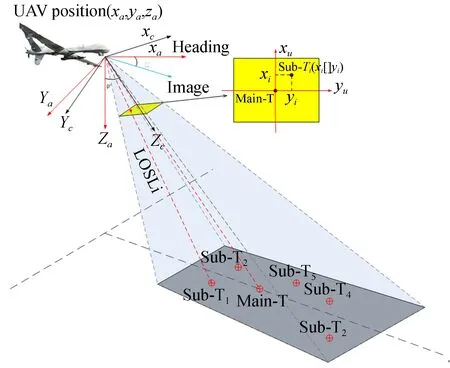
图1 多目标定位原理示意图Fig.1 Schematic diagram of multi-target localization

3 多目标定位的关键技术

3.1 基础坐标变换

3.1.1 坐标系建立

建立合适的辅助坐标系统是定位解算的基础，本文建立了六个辅助坐标系，分别为大地坐标系，地球直角坐标系，载机地理坐标系，载机坐标系，基座坐标系以及相机坐标系。具体描述如下：(1)大地坐标系C(M，L，H)：建立的基准为国际地球参考系统WGS-84系统，采用经纬度和大地高(M，L，H)表示空间任一点的位置，其中L代表经度，M代表纬度，H代表大地高。(2)地球直角坐标系G(Og-XgYgZg)：根据参考椭球面建立的笛卡尔直角坐标系，原点为参考椭球面的中心点；Z轴由原点指向地球北极；X轴由原点指向本初子午圈与赤道圈在椭球面上的交点；Y轴与X轴,Z轴形成右手坐标系法则。地球直角坐标系中空间任一点的坐标值用(xg，yg，zg)表示。(3)地理坐标系S(Os-XsYsZs)：原点即为载机的位置点，为北东地坐标系。X轴指向正北方向，Z轴指向垂直向下，Y轴与X，Z轴构成右手笛卡尔坐标系。在地理坐标系中任一点的坐标表示为：(xs，ys，zs)。(4)载机坐标系A(Oa-XaYaZa)：载机坐标系与载机地理坐标系具有相同的原点，其X轴指向机头方向，Z轴指向载机垂直向下，Y轴与X，Z轴共同组成右手坐标系。(5) 基座坐标系B(Ob-XbYbZb)：原点与载机坐标系重合，Z轴垂直安装基准水平面向下，X轴指向机头，Y轴与X，Z轴共同组成右手坐标系。(6)相机坐标系T(Ot-XtYtZt)：原点位于相机的投影中心位置，Z轴为视轴线指向方向，Z轴垂直向下时，X轴指向飞机正前方，Y轴与X,Z轴共同组成右手坐标系[11-13]。

3.1.2 坐标系转换过程

大地坐标系是以WGS-84参考椭球模型为基准建立的，因此空间一点的大地坐标值表示(M，L，H)到地球直角坐标系(X，Y，Z)的转换可以通过几何关系得到：

X=(N+H)cosMcosL,

Y=(N+H)cosMsinL,

Z=(N(1-e2)+H)sinM,

(1)

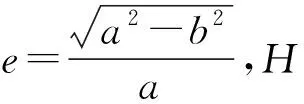
根据组合导航系统(POS)给出的飞机经纬高信息(Ma，La，Ha)，可使用公式(1)得到其地球直角坐标表示(Xa，Ya，Za)。

根据图2(a)中地球直角坐标系与地理坐标系的定义和位置关系，根据空间坐标系转换原理，得到地理坐标系转换到地球直角坐标系的过程为：绕Ys轴旋转角度90°+Ma，之后绕Zs轴旋转角度-La，最后分别沿Xs，Ys，Zs平移(Xa，Ya，Za)，由此可完成转换过程，具体的转换矩阵可表示如下：

(2)

(3)

其中:CL=cosL，SL=sinL，R′用于空间矢量的坐标转换，而R用于空间点坐标的坐标转换。(Ma，La，Ha)表示飞机位置信息。

根据图2(b)中给出的关系可知，载机坐标系是地理坐标系经过一定的姿态角度转换得到，飞机组合导航系统可实时测量飞机三轴姿态角(航向、俯仰、横滚)(λ，θ，κ)，由此可得到二者的转换过程：载机坐标系先绕Za轴旋转角度-λ，之后绕旋转后的Ya轴旋转角度-θ，最后绕Xa轴旋转角度-κ，转换矩阵可表示如式(4)所示。

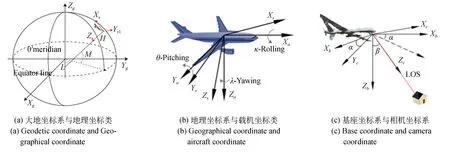
图2 各标系定义及其关系Fig.2 Definition of coordinate systems and their relations

光电平台在安装到飞机上时，光电平台的基准坐标系与载机的坐标系会存在对准的偏差角，这些角度可在安装完成后通过地面标校得到，安装的方位、俯仰和横滚偏差角分别表示为(f，t，p)，转换过程与公式(4)方式类似。其转换矩阵可表示如式(5)所示：

(4)

(5)

光电设备在对感兴趣区域进行侦察时，相机随转台转动，使视轴线LOS指向视场中心目标，此时相机坐标系相对基座坐标系有方位角α和俯仰角β。转换矩阵可表示为：

(6)

3.2 多目标定位模型的建立

3.2.1 主目标定位

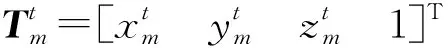
图3 坐标转换过程Fig.3 Coordinate transformation process

根据齐次坐标转换方法，可以得到主目标在地球直角坐标系下的坐标值[14]：

(7)

目标的地理信息(即经纬高)可根据其地球直角坐标系下的坐标值，采用迭代法进行求解。规定北半球纬度为正，南半球纬度为负；东经为正，西经为负。迭代公式的初值由公式(8)给出，使用公式(9)进行迭代。

N0=a

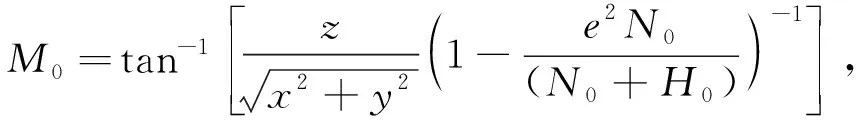
(8)

(9)

经过4～5次迭代后，该方法可保证H的计算精度达到0.001 m，纬度M的计算误差达到0.000 01″级别，精度可满足机载定位需求。

经度计算方式如下:

(10)

其中，

(11)

3.2.2 基于DEM的次目标定位

对光电平台视场中次目标的定位方法基本原理为：通过坐标转换得到目标矢量，再经过计算目标矢量与椭球面的交点坐标，进而得到次目标的位置信息。

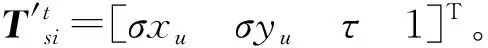
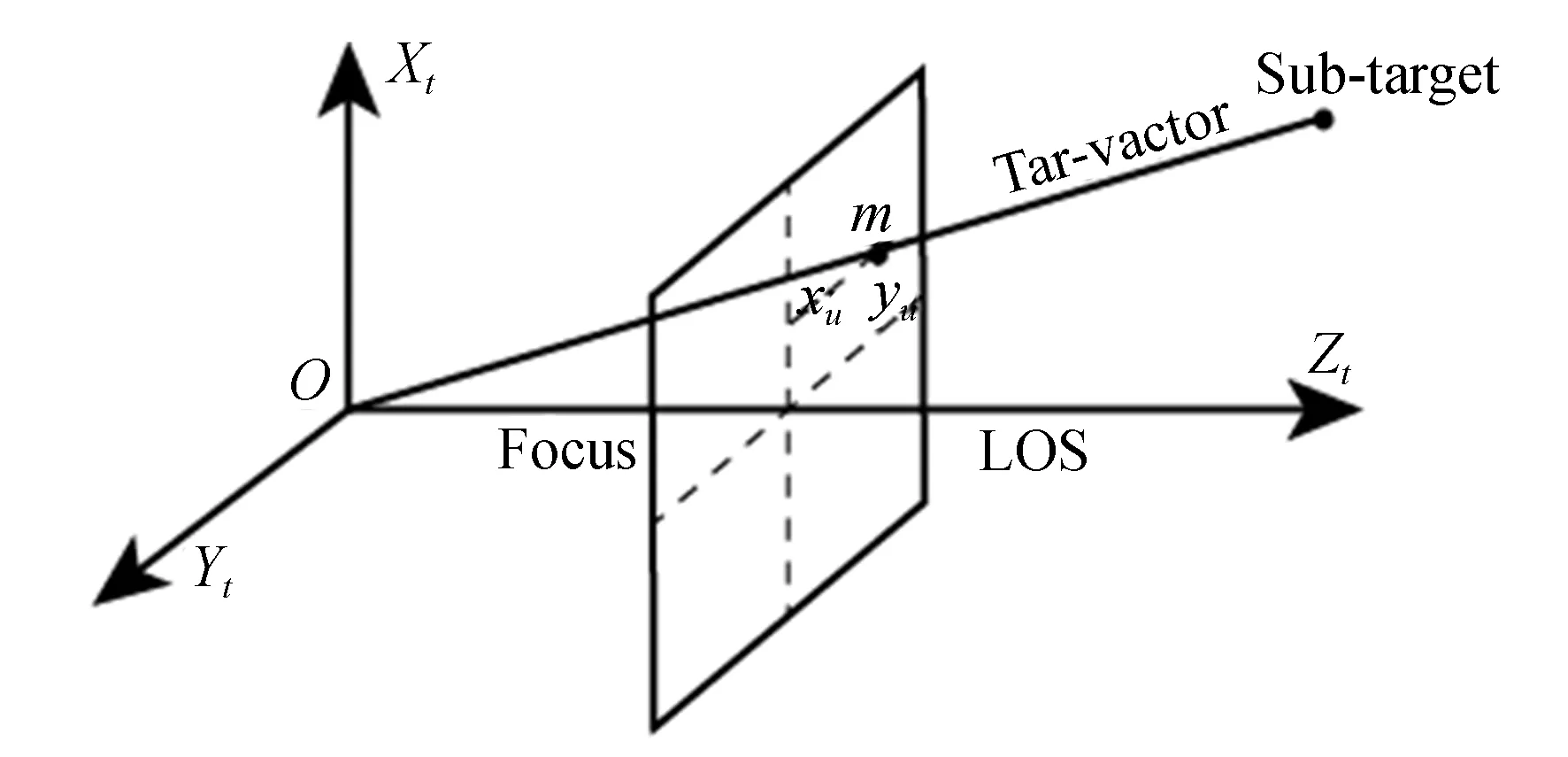
图4 次目标成像原理图Fig.4 Diagram of sub-target imaging principle

根据章节3.1.2中的坐标转换过程，得到目标矢量在地球直角坐标系下的坐标表示：

(12)

(13)

假设拍摄目标高度为h，如图5所示，则根据地球椭球面计算公式，建立新的目标椭球面公式如式(4)：

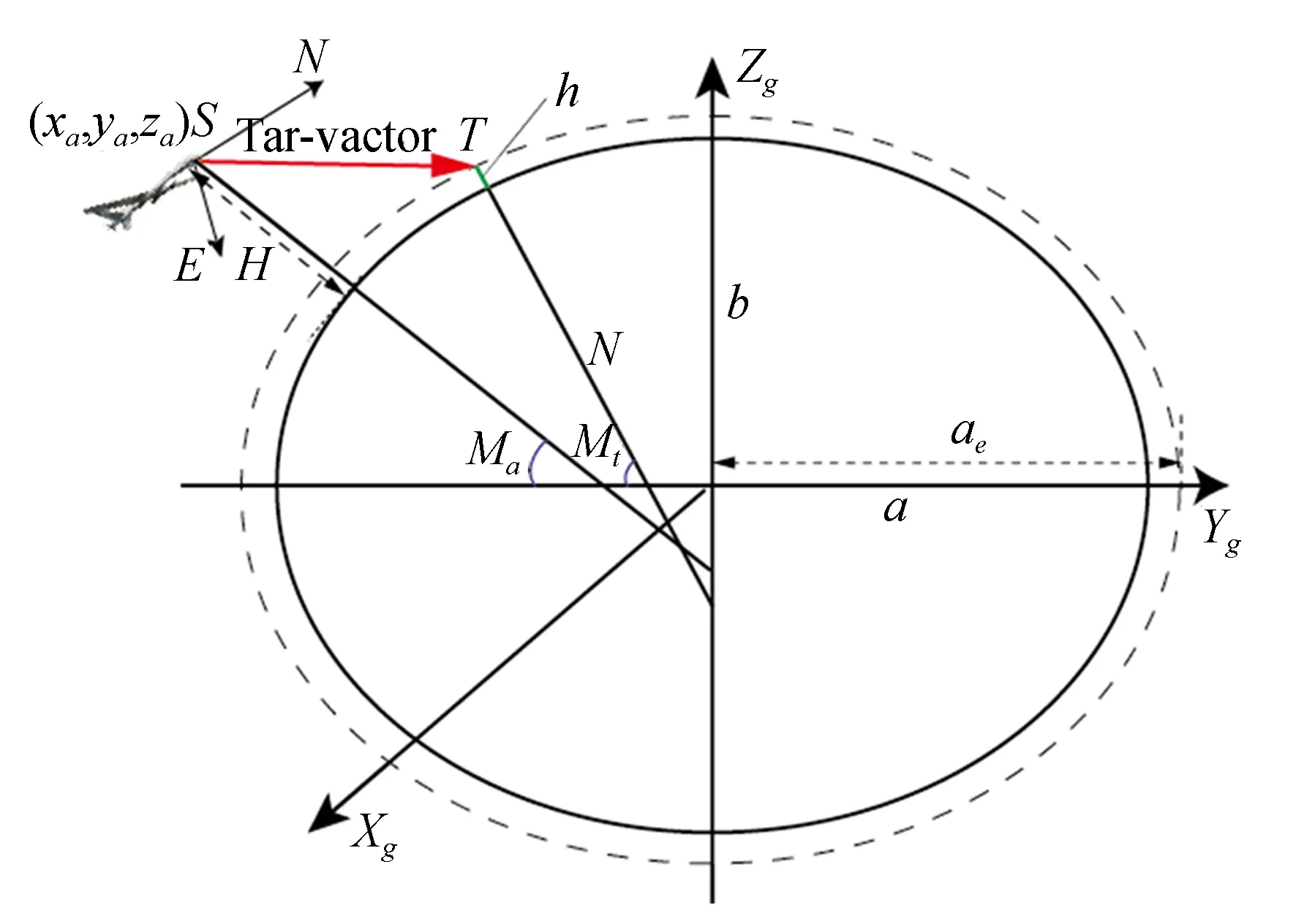
图5 次目标定位原理图Fig.5 Schematic of the sub-target positioning

(14)

结合式(13)和式(14)可得到目标位置计算方程式如式(15)：

(a+h)2(b+h)2=0.

(15)

传统多目标定位算法假定侦察目标区域为平坦地面，因此，在对次目标位置进行解算时，假定其高度h与主目标相同，并以此为前提完成对次目标位置的解算[5]。该方法在用于地势高度起伏比较明显区域的目标时，会导致很明显的定位偏差。如图6(a)所示，次目标点的位置位于红色点位，但是使用传统多目标定位方法时，解算出的次目标点位置为绿色点，这明显影响了定位的效果(彩图见期刊电子版)。

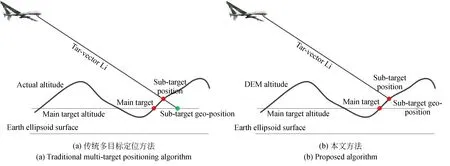
图6 山丘区域次目标定位效果图Fig.6 Schematic of sub-target geo-position in mountainous regions

为解决上述问题，提高多目标定位中次目标的定位精度，本文提出在定位方法中加入数字高程模型。数字高程模型(DEM)是针对地形的数字建模过程，它利用有限的高程数据实现对复杂地面的近似模拟，可表征地表高度信息。目前在全球应用比较广泛的DEM数据主要有美国地质调查局的GTOP30数据，美国国家航空局(NASA)和美国国防部国家测绘局(NIMA)的联合数据SRTM以及NASA和日本经济产业省的(METI)联合的ASTER GDEM，其中ASTER GDEM成像较新，空间分辨率较高，目前应用也最为广泛，其分辨率可达到1″×1″(相当于30 m栅格分辨率)，采用GeoTiff图片格式，每个文件覆盖地球表面1°×1°。可通过Matlab等软件来读取DEM图片中各点的高度信息[15]。

使用DEM信息对次目标定位的原理如图6(b)所示，根据DEM信息，可以准确地获取目标位置的实际高度h，然后通过图5所示的求解方法来计算目标的地理位置信息，该方法可以有效减少地形起伏对次目标定位精度的影响。 基于DEM的目标定位方法的具体解决方案原理如图7所示。该方法可有效降低地势起伏对次目标定位精度的影响。

基于数字高程模型对次目标定位可通过迭代收敛的方法实现。如图7所示，取侦察区域的DEM中的最大值Hmax作为运算初始值H0，通过定位算法，计算得到其对应经纬度(M0，L0)，根据DEM模型可查找出该经纬度对应的高度信息h0，若H0-h0>0，则取H1=H0-εh，由此可进行迭代运算。经过n次迭代后直到出现Hn-hn<0为止，由此可得到次目标的位置信息(Msi，Lsi，Hsi)。通过该方法可将次目标的高度误差控制在εh以内，可有效提高目标定位精度。

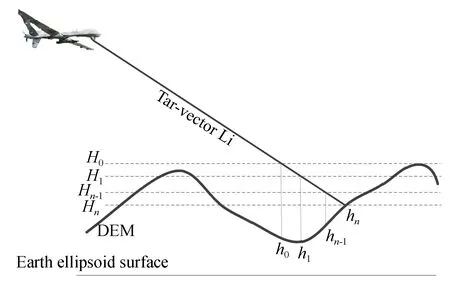
图7 基于DEM的定位方法原理图Fig.7 Diagram of geo-position based on DEM

然而，通常在获取目标区域数字高程模型时，难以避免会存在一定误差值，例如NASA与METI发布的全球数字高程信息ASTER-GDEM-V2，其高程精度在不同区域误差可达5～30 m不等，这些高程误差无疑将影响次目标的定位精度。为减小这一误差的影响，本文结合机载光电设备特点，对高程误差进行修正，以提高定位精度。

从章节2.2.1中可知，光电侦察吊舱可实现对主目标的定位，并由此可得到主目标的高度信息，在实际应用时，该高程信息存在误差φ1，该误差值可通过飞行前的仿真分析得到，假设该目标区域数字高程均方根误差φ2，本文引入误差系数ω，令:

(16)

由此可认为主目标修正后的目标高度：

H=ωH1+(1-ω)H2,

(17)

其中：H1表示主目标测量高度，H2表示主目标在数字高程模型中的高度值。

本文进行多目标定位是针对光电侦察设备同一视场的多个目标，由于视场区域较小，有理由认为这一区域的数字高程误差值相同，因此可得到该区域任意位置修正后的高程信息为：

h′=h+(H-H2)=h+ω(H1-H2).

(18)

多目标定位方法过程如图8所示。结合DEM信息和主目标高程数据，经过迭代运算，可得到次目标的位置信息(Msi，Lsi，Hsi)。

图8 本文多目标定位算法流程图Fig.8 Process of multi-target positioning method by this paper

3.3 多目标定位的自适应滤波

基于DEM的多目标定位精度受测量单元误差噪声的影响，采用合适滤波方法可对噪声信号有一定抑制作用，从而提高定位精度。分析各种定位算法的优缺点，考虑本文算法可用于动态或静态目标，本文采用卡尔曼滤波算法进行数据融合处理，以提高定位精度，而结合实际测量噪声的不确定性，为提高滤波模型的准确性，减小滤波发散风险，本文采用优化的自适应滤波方法[16-17]。

卡尔曼滤波“当前”状态是根据上一状态量解算出来的，设采样时间为T，则目标的运动状态方程：

X(k)=AX(k-1)+BU(k-1)+W(k-1),

(19)

其中X(k)表示在k时刻目标的状态量：

X(k)=[x(k),vx(k),y(k),vy(k),z(k),vz(k)]T，

其中状态变量x(k),vx(k),y(k),vy(k),z(k),vz(k)分别表示目标在经度、纬度和高度方向的位置和速度。由于系统没有控制量，因此B(k) = 0，A表示系统状态转移矩阵：

W(k)表示系统的状态噪声，分布类型为高斯噪声序列，其期望值为q(k)，协方差为Q(k)。

系统的观测方程如下：

Y(k)=HX(k)+V(k)，

(20)

其中：Y(k)为系统测量值，表示目标在k时刻的测量值，Y(k)=[yx(k),yy(k),yz(k)]T，分别表示测量得到的经纬高信息，H表示系统观测矩阵：

V(k)表示观测噪声，分布类型为高斯噪声序列，其期望值为v(k)，协方差为R(k)。由此可得卡尔曼滤波器的递推方程如下：

X(k/(k-1))=A(k)X(k-1)，

P(k/(k-1))=A(k)P(k-1)AT(k)+Q，

X(k)=X(k/k-1)+K(k)(Y(k)-HX(k/k-1))，

P(k)=(1-K(k)H(k))P(k/(k-1)).

(21)

由以上公式可知，噪声是卡尔曼滤波器的重要组成部分，噪声值估计的准确性将影响滤波器的性能。一般情况下，标准卡尔曼滤波默认观测噪声和系统噪声为高斯白噪声，而实际应用中，噪声值是难以预估的，本文根据统计学原理，采用相当数量误差的算术平均值代替误差的期望，利用这些误差和其期望得到误差的近似方差值。根据统计学原理，这样的代替是一种无偏估计。

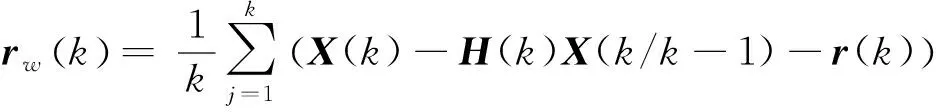
(22)

使用公式(21)可推算出可替代估计的观测噪声和系统噪声的统计量。其中q(k)可表示为系统噪声的期望，r(k)可表示为观测噪声的期望，将qw(k)中每个元素的平方作为矩阵对角元素，其他元素均设置为0的矩阵即为Q(k)，将rw(k)中每个元素的平方作为矩阵对角元素，其他元素均设置为0的矩阵即为R(k)。对于时变系统而言，新旧数据不可一概而论，应逐渐剔除过于陈旧的数据，增大新数据的权重，本文采用一种简便实用的方法完成新旧数据的剔除，根据数据的特点，可使用当前状态前的200帧数据完成对噪声统计的无偏估计，这样可随着新数据的采集不断剔除旧数据，由此可实现对噪声的实时、准确估计，从而准确完成对状态量的估计。

4 实验与分析

定位误差分析是判断一种定位方法科学与否的重要依据。本文进行了多种仿真模拟实验和实际飞行实验，以充分体现算法的性能。从算法的理论分析和其他文献的研究中可知，多目标定位算法中主目标的定位精度主要受各测量单元精度和测量距离的影响，且针对此方向的研究较多，本文不再进行过多阐述。影响次目标定位误差的环节除了上述主目标的影响因素外，还包含目标位置高度误差、测量斜距等，针对此方向的研究较少。本文将对此进行着重分析。

4.1 算法仿真试验及有效性验证

首先通过仿真模拟的方法来验证本文算法的可行性及定位精度。为尽量模拟实际工程应用环境，本文采用蒙特卡洛法进行模拟分析，蒙特卡洛法是通过计算机产生符合条件的随机数据，用于替代实际试验中难以获得的数据[18]。试验中采用的各参数的误差分布均是根据各测量单元产品说明书提供的标定值[19]确定的，如表1所示。试验中采用的数字高程模型为NASA发布的ASTER GDEM-V2，为真实地球高程模型，分辨率可达到1″×1″(经度，纬度)，每张图片覆盖范围为1°×1°，包含3 600×3 600个点高度信息，根据经纬度位置信息，使用Matlab等软件可读取出DEM图片中对应点的高度信息。其在试验测量区域的平均误差为15 m。

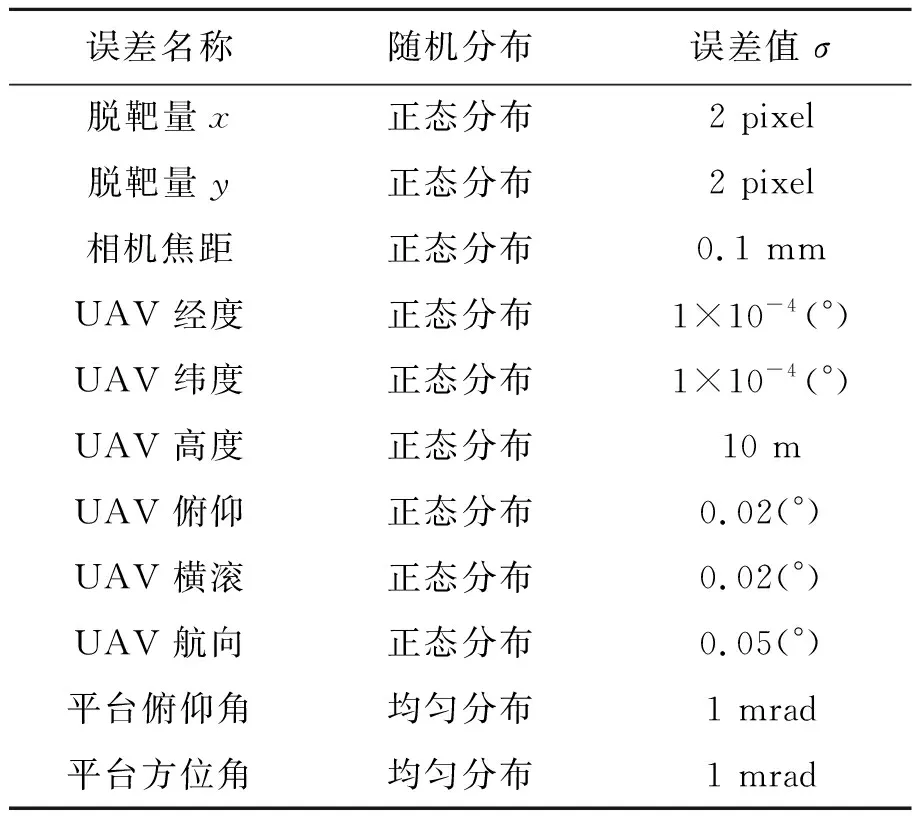
表1 随机误差分布表

为验证本文方法在对地势起伏明显区域的目标定位时的精度，在一片地势高度变化明显的区域图像中选取高度不同的各目标进行定位，仿真中载机和平台参数如表2所示。

表2 地理信息定位名义值

为充分体现误差特性，对图像中每个目标点均采用蒙特卡洛法，取100次随机变量进行仿真计算，得到仿真结果如图9所示。

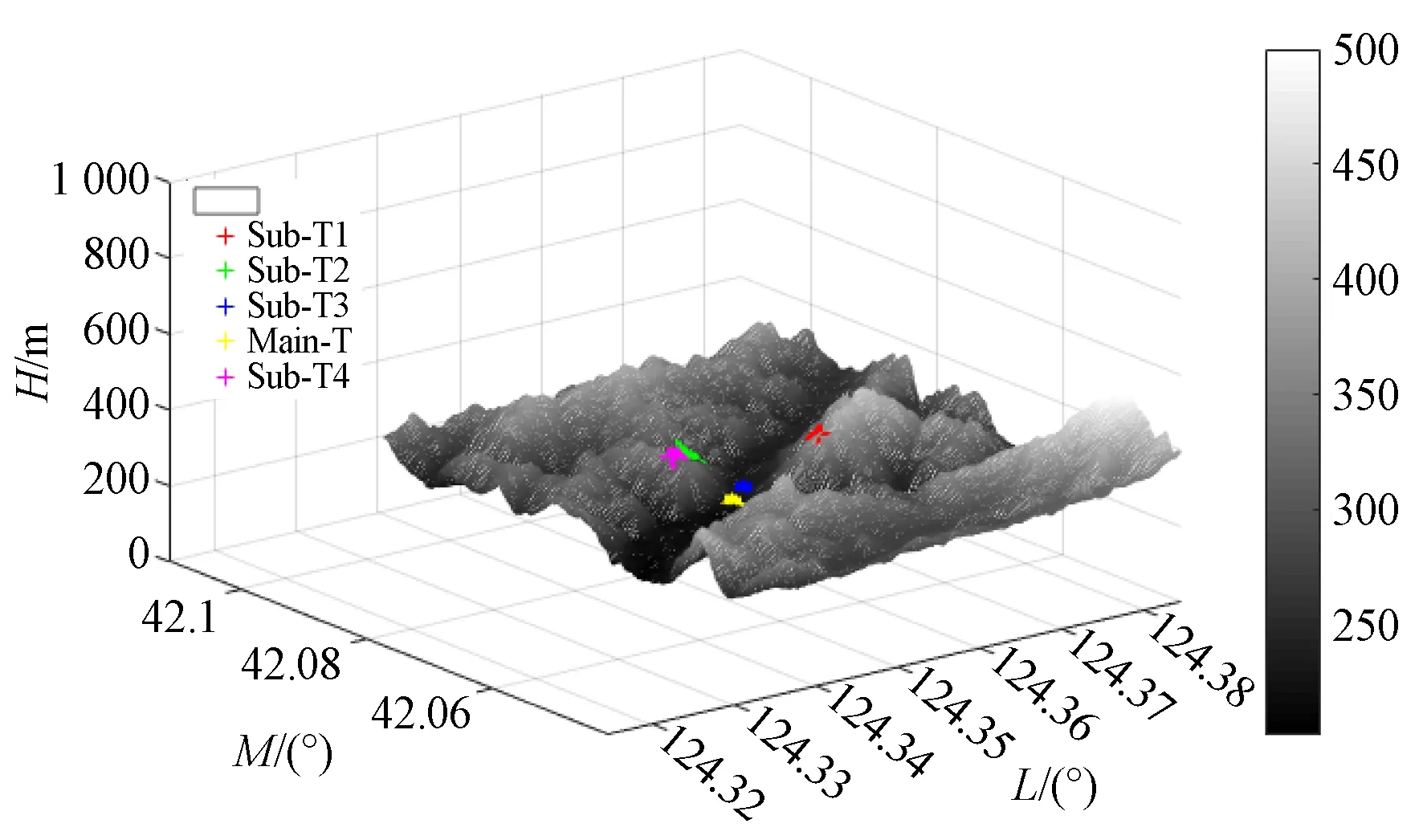
图9 基于DEM的定位结果Fig.9 Location results based on DEM

图中Main-T表示主目标，Sub-Ti为各个次目标。主目标高度误差为7.2 m，根据公式(18)，得到修正后DEM误差为9.73 m。相比原高程模型，精度提高了5.3 m。

为证明本文算法相比传统的多目标定位方法[5]的优势，在相同的目标位置区域采用传统的多目标定位方法进行模拟，得到仿真结果如图10所示。

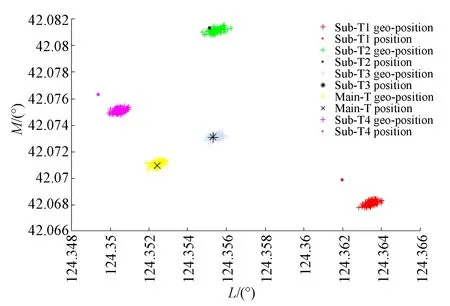
图10 传统方法定位结果Fig.10 Location results based on traditional method

试验中，目标定位精度通常采用平面均方根误差(RMS)进行评价。根据WGS-84坐标系，假定目标位置真值为(Mm，Lm，Hm)，则其对应的子午圈半径可表示为：

进而可得到评价目标定位精度的平面误差：

(23)

仿真试验得到的结果汇总如表3所示。

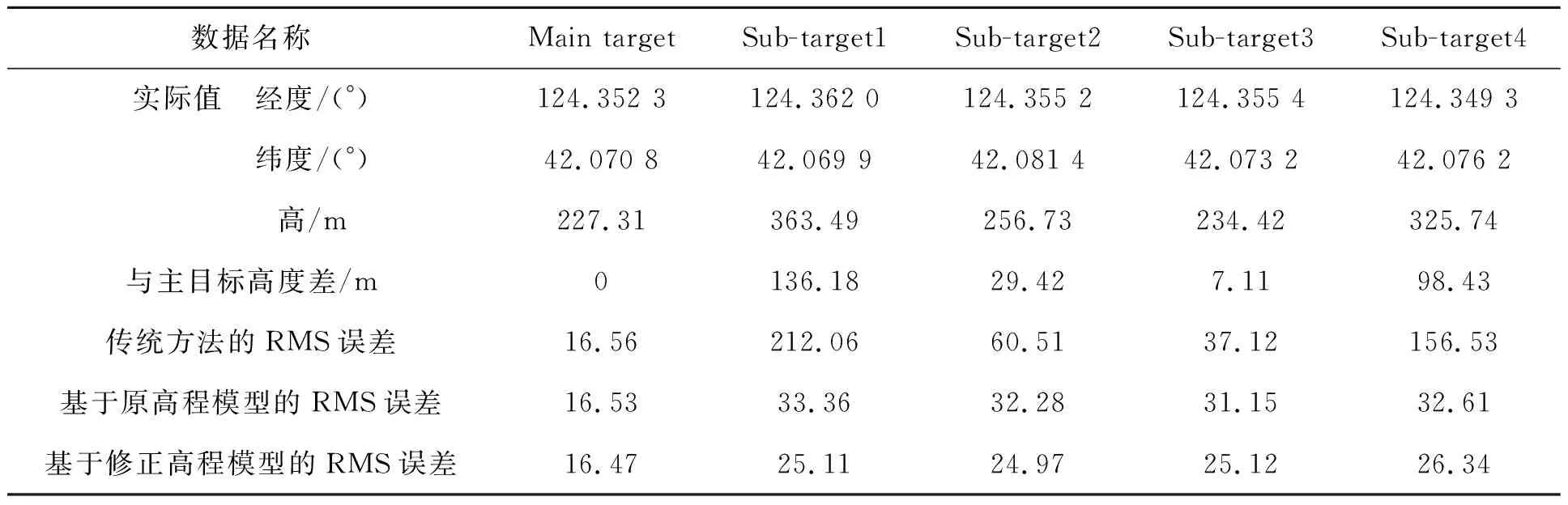
表3 定位误差结果

从表3中结果可知：(1)采用本文算法目标定位算法结合ASTER GDEM-V2高程模型，可实现对地表区域的多目标定位，验证了算法的有效性。(2)本文的多目标定位方法相比于传统方法，主目标定位精度基本保持一致，而各个次目标的定位精度均有明显的提升，且经过修正高程模型，定位精度可得到进一步提高。体现出本文算法的优势。

测试区域地面起伏越明显，即次目标与主目标的高度差越大，则传统多目标定位误差越大，而基于DEM的多目标定位精度则基本不受影响，为进一步量化分析这一结论，本文通过仿真试验分析了高度差对两种定位算法的精度影响。

图11中蓝色曲线表示传统多目标定位方法次目标定位结果随高度差的变化曲线，红色曲线表示基于DEM定位方法的结果(彩图见期刊电子版)，为避免偶然误差，采用蒙特卡洛法，实验中每个点的误差值为1 000次仿真实验误差值的均方根。通过分析图11两种方法误差曲线图可知，随着次目标与定位主目标的高度差距变大，传统多目标定位方法的定位误差基本呈线性增大，而基于DEM的多目标定位方法误差稳定，不受地势变化的影响，其误差量主要受视轴指向误差影响，在地势平坦区域，两种定位方法效果相似，但在地势崎岖的山区或丘陵地带，本文方法具有十分明显的优势。

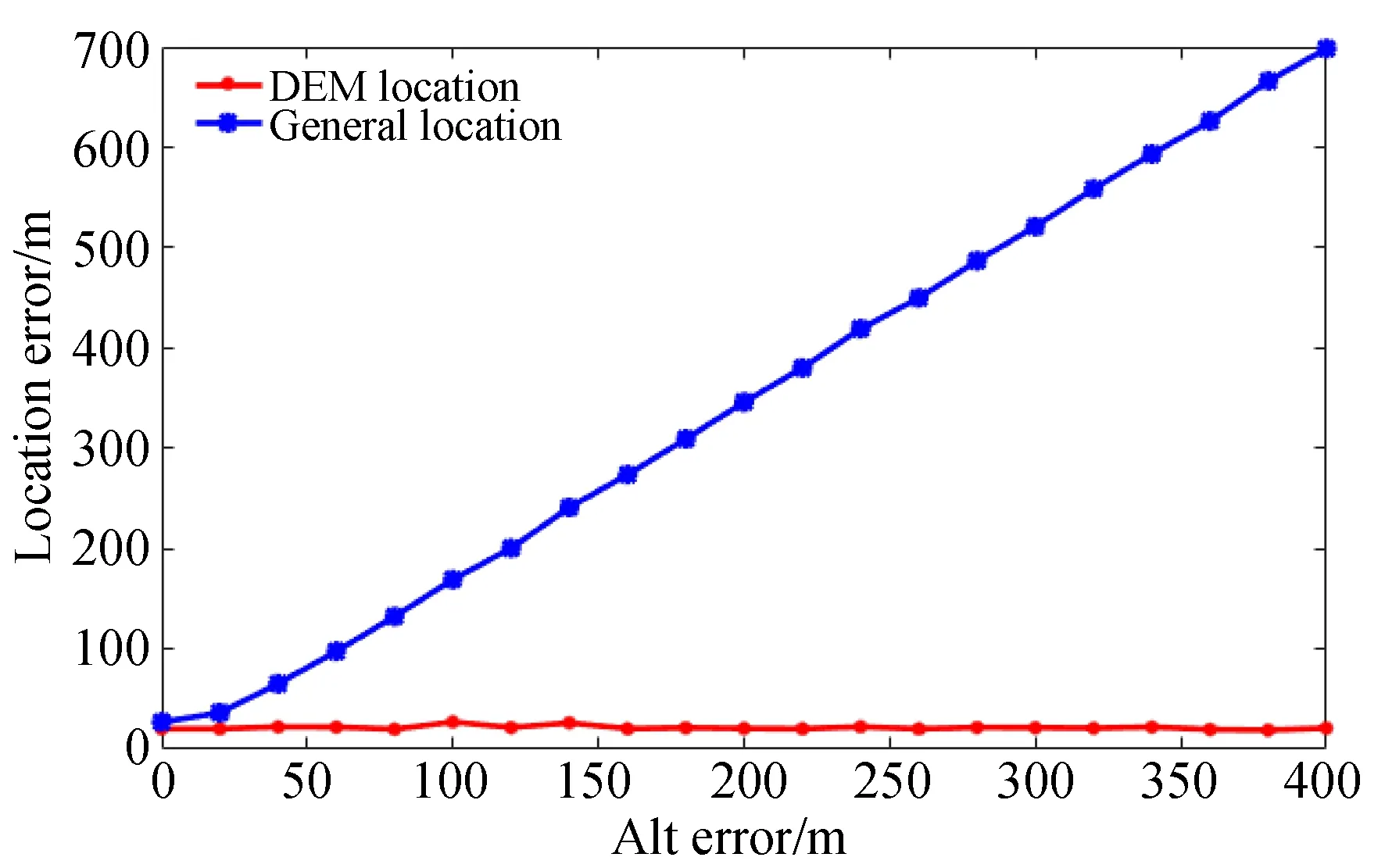
图11 定位误差随目标区域高程变化图Fig.11 Location error curve with altitude difference

4.2 俯仰角和测角误差对定位精度影响

机载光电平台的一般工作方式是：无人机挂载光电设备在空中平稳飞行，地面控制人员操作光电平台进行方位和俯仰角变化，对感兴趣位置进行侦察测量[20]。在进行定位解算时，由于飞机导航系统、光电平台测角单元及提取像素坐标等误差的存在，导致解算得到的视轴线与实际视轴线存在一定的误差角，称为视轴指向误差，从理论计算方法可知，视轴指向误差只与各测量参数误差有关，不受目标位置变化影响。经分析，随着光电平台俯仰角度的变化，视轴指向俯仰角会发生变化，此时，相同视轴指向误差角下，定位误差将发生变化。

如图12所示，随着视轴线仰角的增大，相同的视轴线误差会导致更大。为量化分析这一结果，进行了试验验证。仿真中飞机的位置和姿态如表2所示，仿真平台俯仰角从0开始逐渐增大，得到主目标和次目标随俯仰角变化的定位误差曲线，如图13所示。

图12 定位误差随视轴俯仰角变化示意图Fig.12 Schematic of location error changing with pitching angle

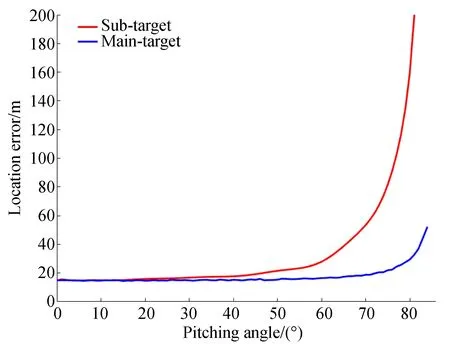
图13 定位误差曲线Fig.13 Location error curve

图13中红色曲线表示使用本文方法得到的次目标定位误差随俯仰角变化的误差曲线，蓝色曲线则表示主目标的定位误差曲线(彩图见期刊电子版)。实验结果表明，当俯仰角度较小(角度值小于50°)时，主目标与次目标定位误差较稳定，且二者误差值相差不大。但随着俯仰角的逐渐变大，两者的定位误差开始有增大趋势，且次目标定位精度开始对俯仰角更敏感。在飞机飞行高度为3 000 m条件下，当俯仰角小于70°时，主目标定位精度在20 m以内，俯仰角小于60°时，次目标定位精度也较平缓，在30 m以内，俯仰角从60°～70°时，次目标定位精度达到50 m，且上升趋势已十分明显，达到80°时，主目标定位精度仍能达到29.2 m，次目标定位误差较大，达到140 m。在实际飞行侦察中，在进行多目标定位时，应保持俯仰角在70°以内，可达到较理想的定位结果，若目标距离太远，俯仰角太大时，可考虑适当升高飞行高度，以减小俯仰角，提高定位精度。

此外，视轴指向测角误差是光电平台中影响定位精度的主要因素，针对主目标算法分析测角误差对定位精度影响的文献较多，在此不再详述，本文主要分析次目标受测角误差的影响。通过对比分析和仿真试验，得到不同测角误差下对次目标的定位误差曲线如图14。

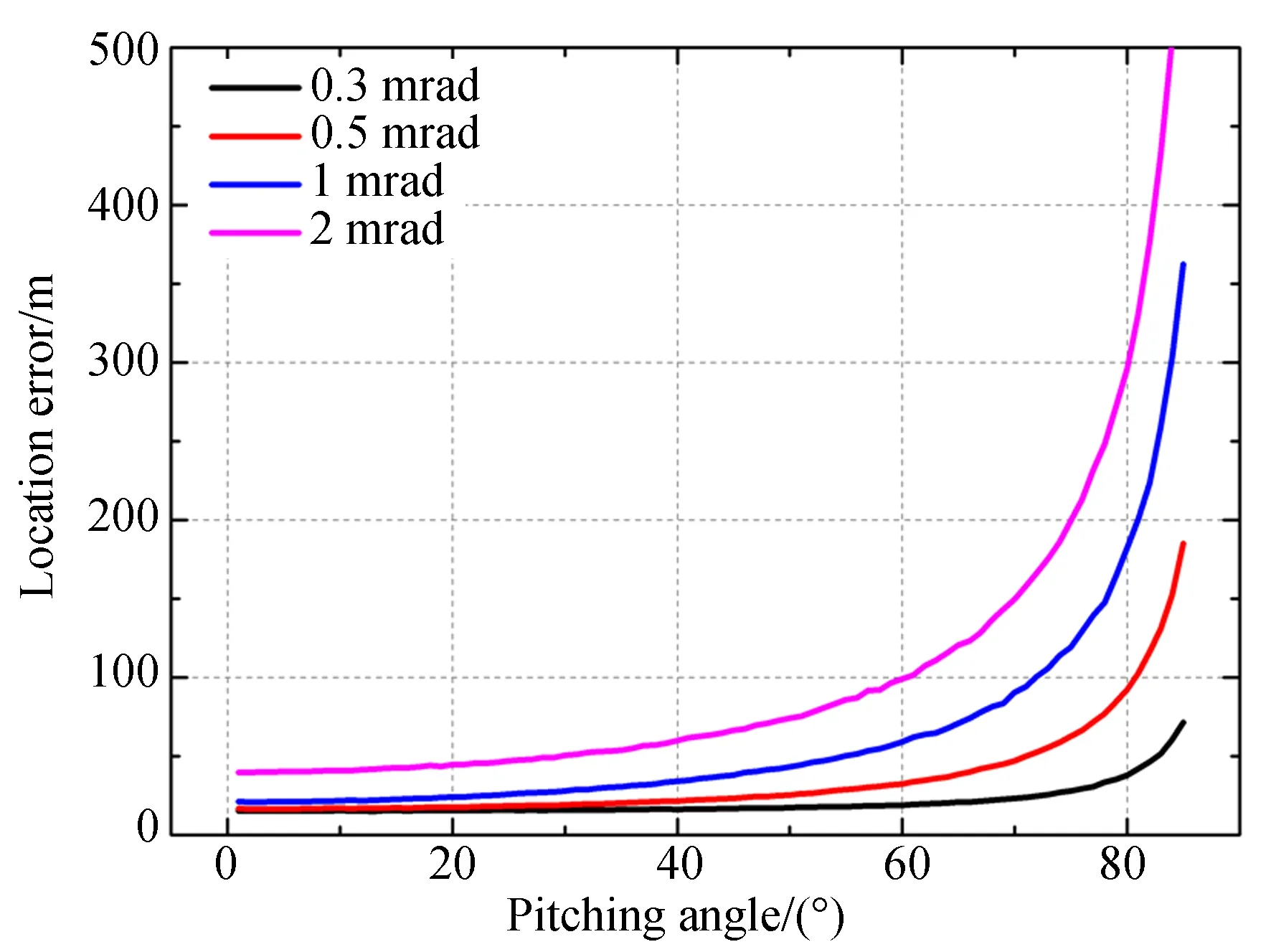
图14 不同测角误差的定位误差图Fig.14 Location error curves for different angle measurement errors

由图14曲线可知，随着测角误差增大，对次目标的定位误差也会随着增加，且误差值会更加敏感于俯仰角的变化。

4.3 滤波实验

为验证章节3.3中滤波器对不同类型目标的滤波效果，本文通过试验分析了对三种目标的滤波结果，分别为静态主目标(Main-tar)，静态次目标(Sta-tar)和动态次目标(Mov-tar)，采用本文滤波算法对第一幅图像为起始时刻的400帧图像进行试验，得到滤波前后的三个目标的轨迹如图15所示。

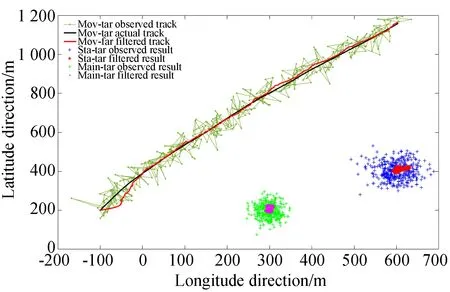
图15 3个目标定位轨迹Fig.15 Localization track of the three targets

图16为滤波前后各个目标的平面定位误差随图像帧数变化曲线。图16(a)、(b)、(c)分别为动态次目标、静态次目标和静态主目标的定位误差曲线。红色曲线表示滤波后的结果，蓝色则表示滤波前结果(彩图见期刊电子版)。

由图16误差分布可知，经过滤波后三个目标定位误差相比原始测量值明显减小，滤波前mov-tar,sta-tar,main-tar的定位误差分别为26.36 m,25.11 m,16.47 m，滤波后误差分别达到11.13 m,10.48 m,6.51 m。从图16中图像帧数可以看出，滤波前定位误差值较发散，对于两个静态目标，前30帧为滤波器的数据积累过程，此时误差较大，30帧后数据快速收敛并趋于稳定平滑，这一结果也在图14中得到验证，滤波后的定位结果明显更聚集。对于动态目标，滤波器的数据收敛速度较慢，前70帧为数据收敛过程，之后则趋于稳定，图15为模拟运动轨迹图，黑色曲线表示目标实际运动轨迹，实心点曲线表示测量得到的目标轨迹，红色曲线表示滤波后轨迹(彩图见期刊电子版)，由图可知，原始测量点位置明显比较分散，滤波后的轨迹则更为平滑，且与实际运动轨迹更贴合。

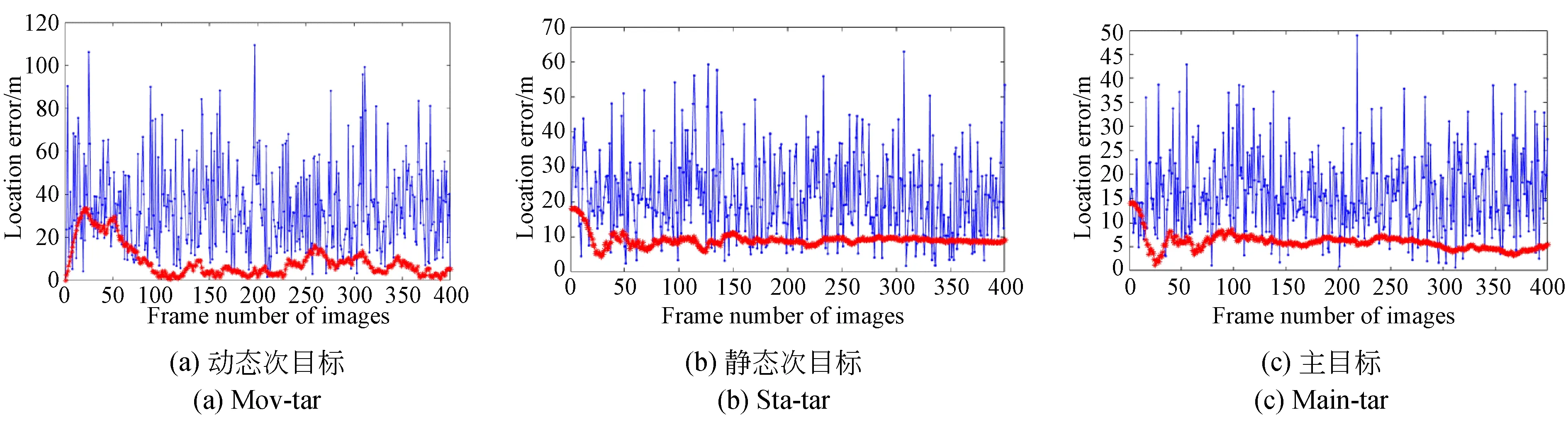
图16 滤波前后的定位误差Fig.16 Location errors before and after filtering

4.4 飞行定位试验

为验证本文方法的实用效果，进行了对多个地面运动目标的实时多目标定位试验，试验中对四辆汽车进行跟踪定位，四辆汽车均带有Geo Explorer 3000 系列GPS接收机作为测量仪器，定位精度可达50 cm，可将其近似看作位置真值。系统选用的数字高程模型在实验区域的高程误差为10m，选用DSP芯片TMS320F28335作为解算芯片，定位解算时间为1 ms，可满足实时性要求。在3 000 m飞行高度，俯仰角约40°条件下对三辆汽车进行定位测量，跟踪过程图像如图17所示(图像部分区域)。为证明本文算法可适应复杂的地形区域，本文选取的试验区域为有复杂高度变化的立交桥路段。

图17 多运动目标航拍视频图像Fig.17 Multiple moving targets in aerial video imagery

由图17试验图像可明显看出，主目标(Main-tat)与次目标1(Sub-tar1)高度基本一致，而次目标2(Sub-tar2)和次目标3(Sub-tar3)均位于立交桥上，与主目标有明显高程差。采用不同的定位算法对实际测量中各目标进行定位解算，得到各目标的解算数据如表4。由表中结果可知，随着与主目标高程差的变大，传统方法的定位误差明显变大，本文方法则基本不受高程变化的影响，且两种方法对比，本文方法定位误差明显小于传统方法，采用滤波方法后定位结果进一步降低，得到实测结果与仿真结果表现基本一致，这也证明了本文算法具有良好的工程适用性。

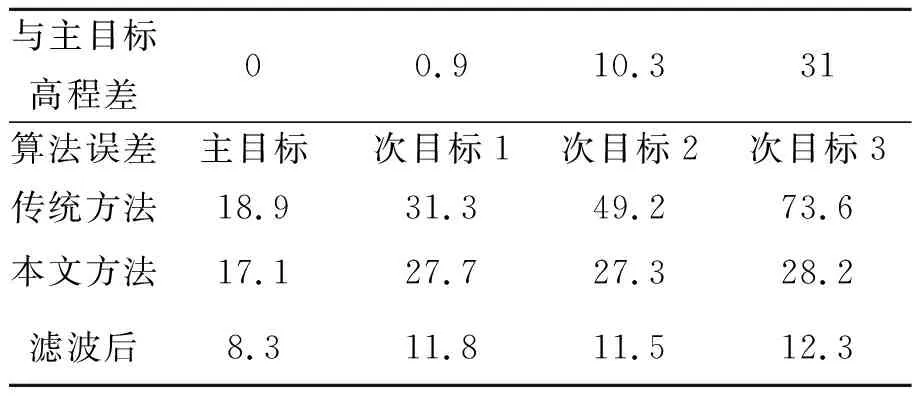
表4 各种方法的定位结果

5 结 论

为提高机载光电设备的侦察测量效率，本文结合现有定位方法的优缺点，提出了一种基于DEM的多目标定位方法，建立了多目标定位模型，并针对定位模型进行了误差分析，提出一种提高定位精度的滤波算法。试验研究表明：(1)在地势起伏区域，本文算法定位精度明显优于传统的多目标定位方法，经过修正高程模型，次目标定位精度也可得到进一步提升；(2)定位误差随俯仰角增大而变大，且次目标定位精度开始对俯仰角更敏感。在飞机飞行高度为3 000 m条件下，当俯仰角小于70°时，主目标定位误差小于20 m，次目标定位精度在50 m以内，俯仰角为80°时，主目标定位精度为29.2 m，次目标定位误差则达到140 m。(3)自适应滤波器对动目标和静目标均有良好滤波效果，滤波前mov-tar、sta-tar、main-tar的定位误差分别为26.36 m，25.11 m，16.47 m，滤波后误差可达到11.13 m，10.48，6.51 m。定位精度提升明显。(4)经过实际的多目标跟踪定位试验，定位结果与仿真结果基本一致。证明了本文算法在实际应用时具有良好的定位效果。下一步将研究如何提高大倾斜角度下的定位精度。