基于噪声子空间矢量的OMP离格DOA估计
赵 洋,石屹然,石要武
(吉林大学 通信工程学院,吉林 长春 130022)
1 引 言
波达方向(Direction of Arrival, DOA)定位和跟踪是自适应天线以及阵列信号处理的重要研究方向,其在网络通信、导航、射电天文、地震勘探、医疗诊断等领域都有深入的应用。DOA估计的基本问题是通过设计算法对同时出在空间某区域内的多个目标信号的空间位置进行估计。近些年发展起来的稀疏表示理论的基本出发点是假设基函数在某变换域中是稀疏的,这点恰恰与DOA空域信号在整个空间区域内稀疏分布相契合,所以稀疏恢复算法正在被广泛用于阵列信号处理领域。
稀疏恢复算法为阵列信号处理提供了新的解决思路的同时也带来了网格量化误差问题。目前几乎所有稀疏表示测向算法[1-5]中均假设DOA信号恰好落在预设网格上,基于此假设阵列信号模型可以通过对整个角度空间的网格化转化为在各个网格点上(on-grid)的线性稀疏重构模型。然而,真实的来波信号在角度空间内连续分布,依赖上述假设建立的稀疏重构模型与真实测向模型之间存在模型拟合误差。随着在整个空间域内划分的网格数的增加这个模型拟合误差在一定程度上会减少,然而由于离散网格数毕竟是有限的,所以此误差无法完全消除。并且增加网格数会带来大计算量的同时也会导致字典相邻原子间的相关性显著增加,这又与稀疏表示理论要求原子间满足有限等距条件(Restricted Isometry Property: RIP)相矛盾,进而对算法运算结果带来影响。
为了克服网格量化误差对测向的影响,研究学者对离格(off-grid)信号场景进行了研究,通过阵列导向的一阶泰勒展开式将网格偏移量引入DOA估计的off-grid模型。文献[6]利用交替迭代优化思想解决压缩感知算法中的重构矩阵存在误差的问题,提出了稀疏全局最小二乘法。然而该算法性能受限于两个正则化参数的选择。文献[7]提出了一种类似基追踪去噪(Basis Pursuit DeNoising, BPDN)的算法对信号和网格量化误差进行联合求解。文献[8]研究了上述off-grid模型进行DOA估计中网格量化误差的理论下限。文献[9]针对DOA估计的off-grid模型提出了一种混合范数优化算法。上述文献均采用基于lp,0≤p≤1 范数约束的凸优化算法进行求解,而对信号DOA和网格量化误差进行联合估计是非凸问题,通常需要交替迭代多次求解凸优化问题,计算量较大且设置正则化参数缺乏统一的理论支撑。
以OMP算法为代表的贪婪算法因其具有计算量小、逻辑清晰、所需先验知识少等优点,被广泛用于稀疏恢复的各个领域。然而以往的文献中利用贪婪算法解决基于off-grid模型的DOA估计问题却鲜有报道。主要原因是这类方法在冗余字典原子间相关性较强时性能显著恶化[10-11],如此会导致的低分辨率使得考虑网格量化误差变得没有意义。事实上由导向矢量展开生成的冗余字典局部范围内原子间具有的强互相关性会导致大多数稀疏恢复算法在处理空间距离相近的一对信号时性能恶化。而贪婪算法通常恰以残差与原子的相关度大小作为判定该原子是否选入支撑集的判定标准,导致此类算法受到冗余字典原子互相关性的影响更为显著。文献[12]说明了贪婪算法无法分辨在同一波束内的多个方向信号。为了提高此类算法的分辨能力,文献[13-14]提出了多级树状匹配追踪模型,文献[15]采用适用与多块拍的场合的DOA估计匹配追踪算法(Multiple Measurement Vector, MMVOMP),文献[12,16-17]分别针对均匀线阵、均匀面阵和非均匀线阵提出基于字典原子扩维的聚焦OMP(Focused OMP,FOMP)算法。但是以上算法以及其他OMP的衍生算法如ROMP[18]CSMP[19]都没从根本上降低此类算法对冗余字典原子间互相关性的依赖性,从而无法真正改善在其用于DOA估计时超分辨能力不足的问题。此时只能依靠增大阵列孔径来提高分辨率,而实际应用中很多特殊场合对阵列孔径的大小有严格限制,如机载雷达。本文从支撑集判定规则角度对此类算法进行修正,设计改进算法以满足分辨率要求,同时考虑了网格量化所带来的误差影响。
2 数学模型
考虑M个阵元构成的均匀线形阵列如图1所示,阵元间距d等于半波长,接收K个互不相关的远场窄带信号的阵列输出为:
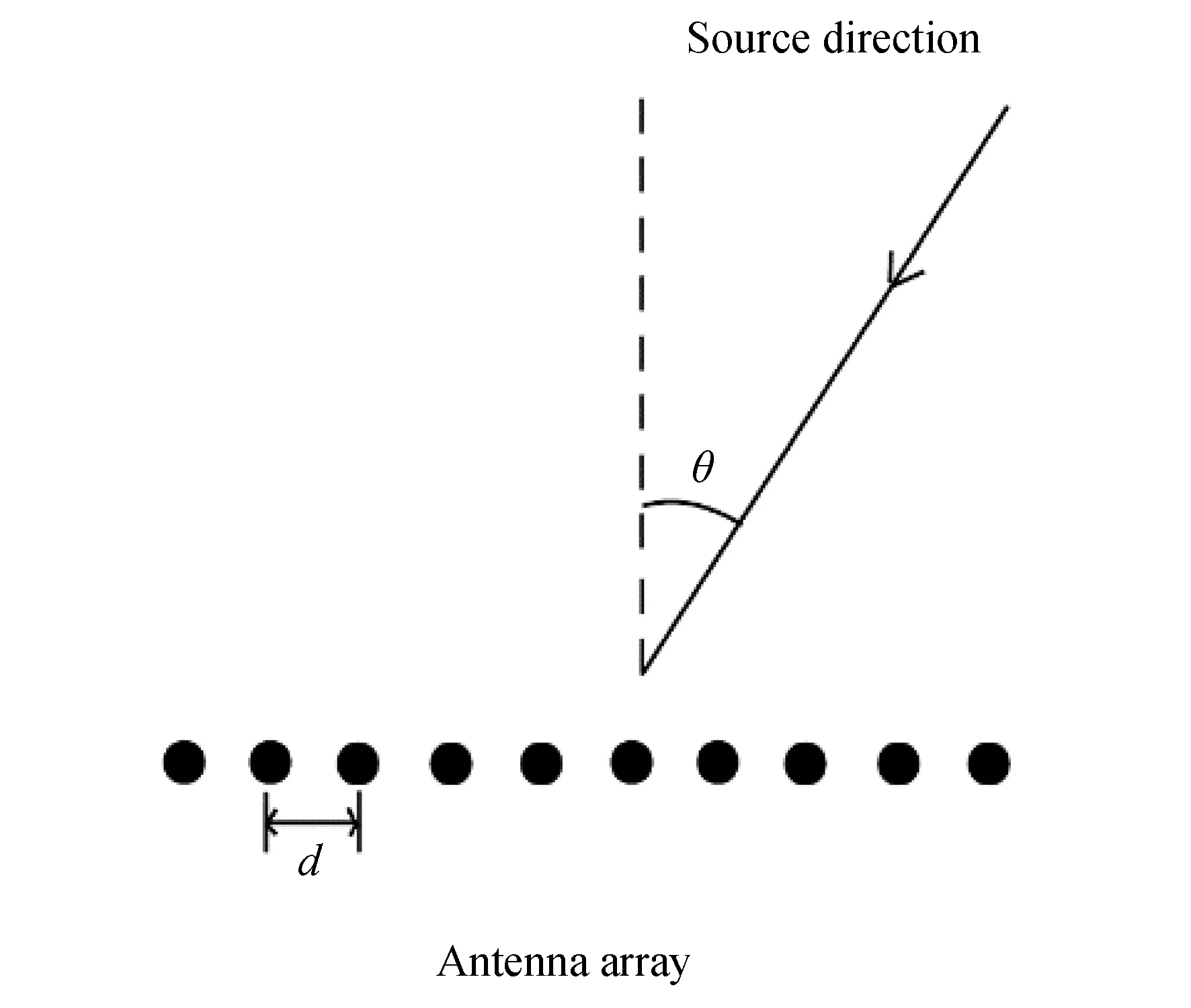
图1 10个阵元构成的均匀线形阵列Fig.1 Uniform linear array composed of ten elements
X(t)=A(θ)s(t)+e(t),
(1)
其中:e(t)为高斯白噪声。根据阵列信号模型,当阵列接收到足够快拍数时,有阵列输出数据可以得到协方差矩阵为:
R=E[XXH]=A(θ)RSAH(θ)+σIM,
(2)
其中:E[·]表示求期望,上标H表示求共轭转置,RS表示信号S的协方差矩阵。当入射信号互不相关时RS为对角矩阵,对角线元素分别为{p1,...,pK},pk为第k个入射信号的功率。此时对(1)进行向量化操作得到:
r=(A*(θ)⊙A(θ))p=Φ(θ)p,
(3)
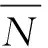
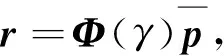
(4)
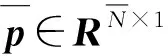
(5)
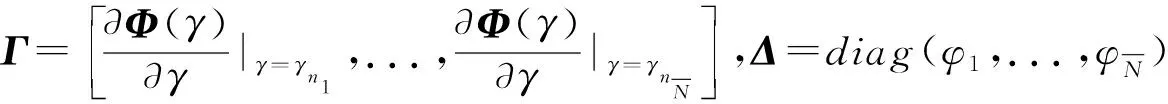
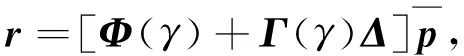
(6)
其中Δ称为模型的量化误差矩阵,当Δ=0时,模型(6)和模型(4)等价,此时所有入射信号恰好落在预设网格上。显然模型(6)考虑到了离格情况的发生,对比模型(4),模型(6)与真实信号模型吻合度更高。
信号协方差矩阵R理论上需要无穷快拍才能精确计算,现实系统中只能通过有限的L次采样计算R的估计值:
(7)
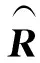
υHΦ(θk)=0.
(8)
依照式(8)对OMP算法支撑集提取规则进行修正,打破对原子间的互相关度的单一依赖。
3 算法实现
(9)
第二步保持p不变,更新Δ:
(10)
其中Δ=diag(φ1,...,φK)。将上述思想嵌入OMP算法框架,同时利用(8)对其进行修正得到噪声子空间矢量离格OMP(NSVOGOMP)算法过程如下:
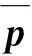
(11)
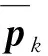
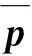
(12)
令∂L(Δk)/∂Δk=0可以得到Δk的对角线上的第nk个元素更新为:
(13)
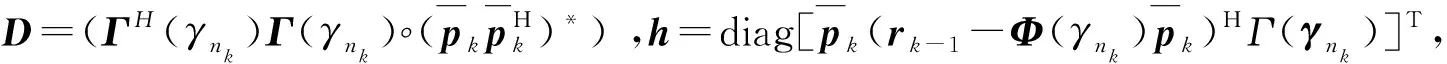
(14)
具体算法流程如下:
该算法的优点是无需已知信号源个数。
第k次迭代:
Step1利用式(11)确定支撑集序号nk和对应的原子Φ(γnk);
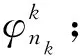
Step3:计算|υHΦ(γnk)|和|υH(Φ(γnk)+Γ(γnk)Δk)|;
Step4:如果|υHΦ(γnk)|≥|υH(Φ(γnk)+Γ(γnk)Δk)|则:
Step5:如果|υHΦ(γnk)|<|υH(Φ(γnk)+Γ(γnk)Δk)|则:
4 仿真实验
本节主要评估文中NSVOGOMP算法的DOA估计性能,仿真实验基于10阵元以相邻阵元间距半波长排列构成的均匀线形阵列为基础围绕验证算法估计的精度与方向分辨能力展开。在实际应用中本文所提算法适用于任意几何结构阵列。实验中要求信号的DOA在角度域以内但是允许落在预设网格以外的任意情况发生。
4.1 实验一:验证支撑集判定规则
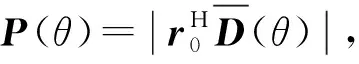
4.2 实验二:NSVOGOMP算法的DOA估计性能
实验二验证了NSVOGOMP算法的DOA估计性能。对于10阵元的ULA阵列,波束宽度BW≈15°,信噪比SNR1,2,3,4=10 dB,设角度域内存在2对K=4个互不相关的远场窄带邻近信号:θ11=20°,θ12=25° 和θ21=-35°,θ22=-40°。实验结果与实验一中算法在相同参数设置条件下进行比较。网格设置在-90°~90°,网格设置步长l为1°。图2显示了三种算法在快拍数为L=100次时的归一化空间谱。
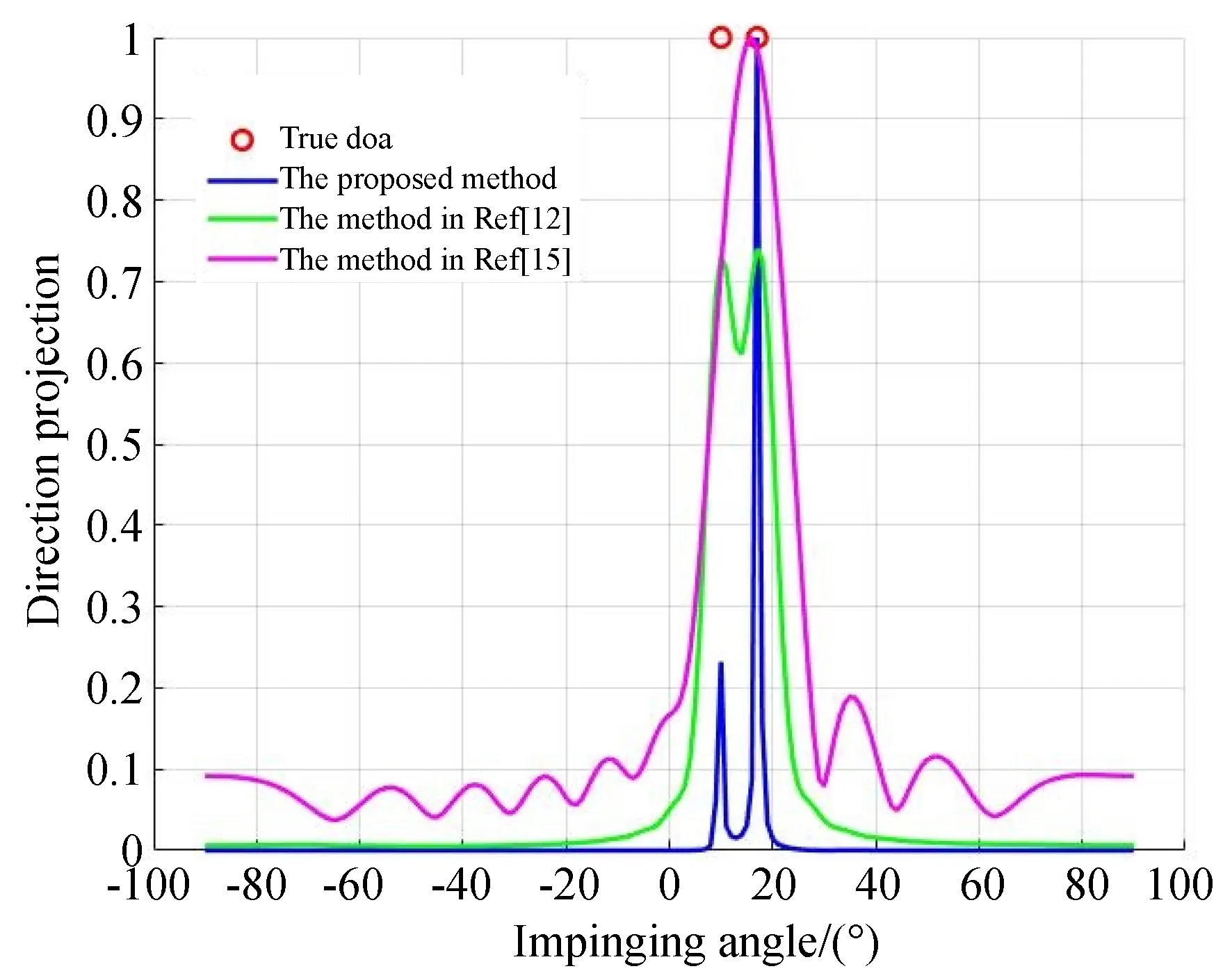
图2 初始残差在字典原子方向上的投影Fig.2 Projection of initial residuals in dictionary atomic direction
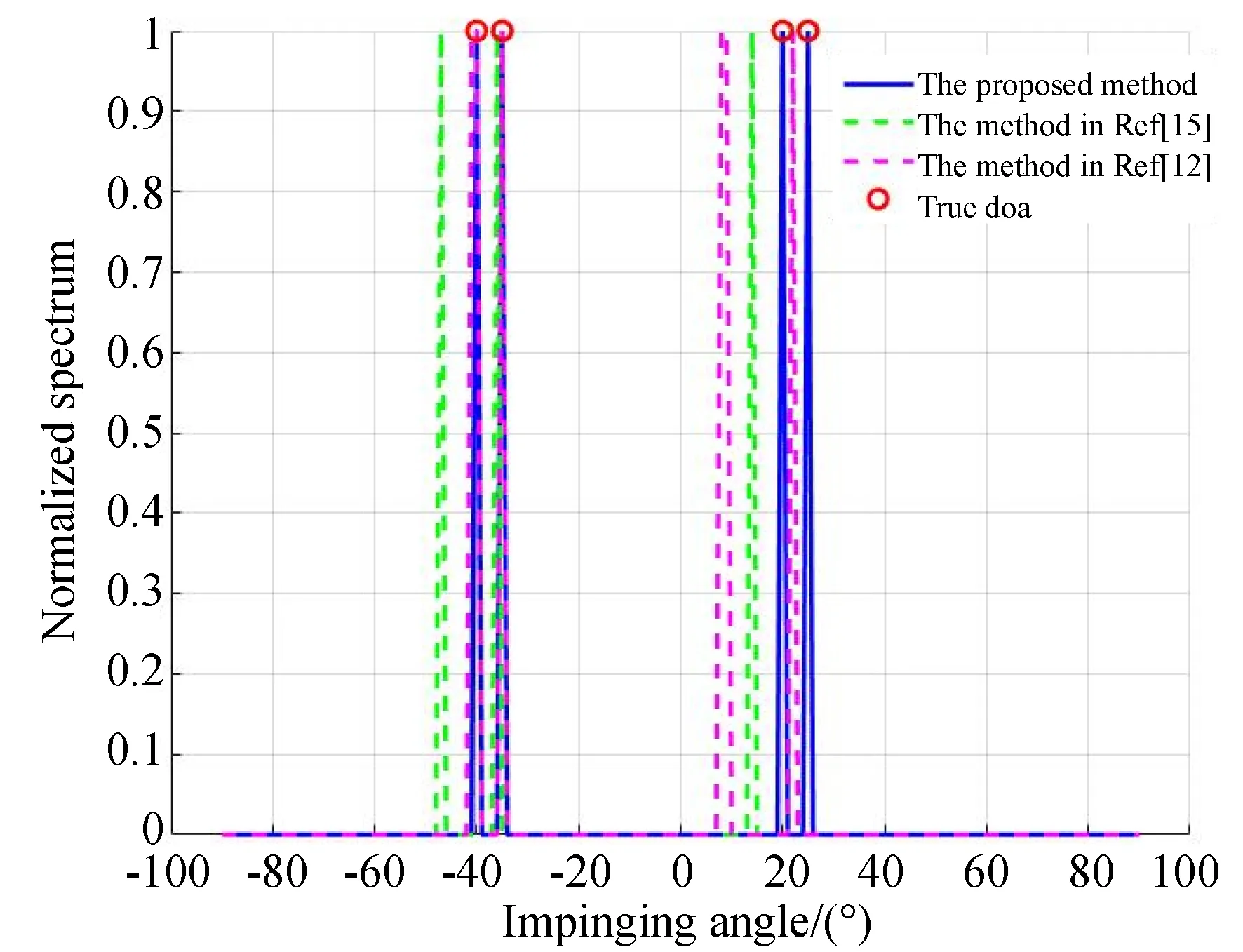
图3 三种OMP类算法的归一化空间谱Fig.3 Normalized spatial spectrum of three OMP algorithms
为了方便进行比较,需要将三种OMP算法的停止条件进行统一,由于不同算法的残差衰减速度不同这里统一设置每种OMP算法迭代次数等于信号源个数。且由于另外两种算法都是直接定义在阵列输出X(t)上的,且FOMP算法的字典中原子维数又与其他两种算法不同,导致空间谱幅值差异较大,为了方便观察本实验对所有空间谱幅度均进行归一化处理。图1中可以看到本文所提出算法对处理互相临近的DOA信号对时比其他两种算法存在优势,在快拍数满足一定数量的时候可以很好的估计出波束宽度以内的一对信号源位置。
4.3 实验三:分离角度偏差实验
实验三为了研究算法进行DOA估计的空间角度分辨能力,本文重复文献[1]中的分离角实验。将实验二中的三种算法与Root-MUSIC算法在相同参数设置条件下进行比较。设有一对等功率信号:θ11=-50°,θ12=-50°+δ°,其中δ以1°间隔从1°增加到50°,每变化一次生成一对信号,每对信号进行100次蒙特卡洛实验,设置信噪比SNR1,2=0 dB,快拍数L=500考察算法对每一对角度估计的偏差:
(15)
从图4可以看到本文所提算法的分辨能力仅次于Root-MUSIC而优于其他两种OMP算法。MMVOMP算法很好的利用了多块拍信息,但是无法分辨一个波束宽度(BW=15°)内的两个信号。利用噪声子空间矢量修正支撑集提取标准为本文算法带来了分辨率上优越性。优于Root-MUSIC使用了全部噪声子空间矢量所以分辨率更高,但是该算法必须依赖于噪声子空间的正确划分,也就是必须假定已知信源个数。
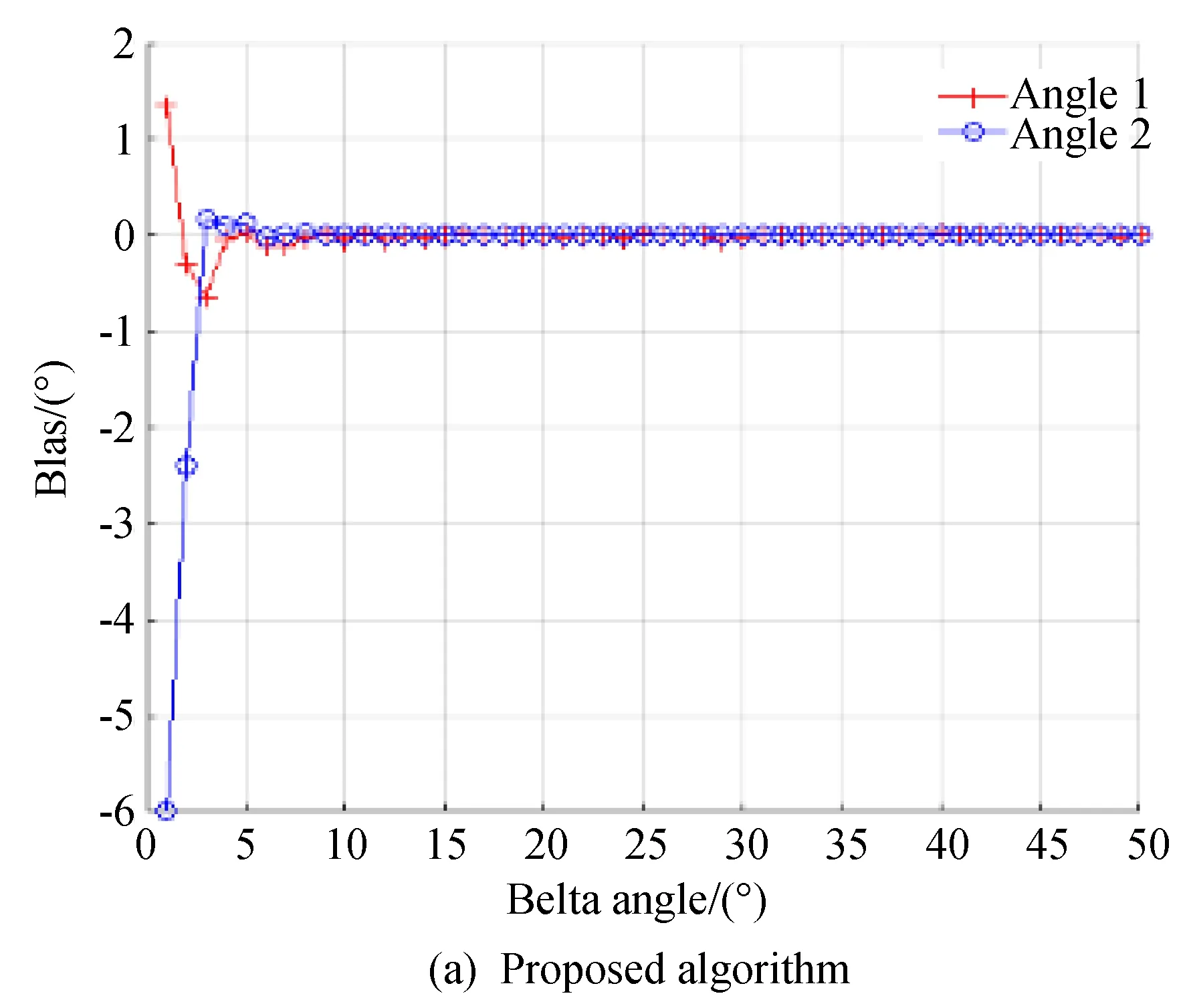
图4 分离角偏差实验Fig.4 Separation angle deviation experiment
4.4 实验四:均方根误差实验
估值值与真实值之间的均方根误差(Root Mean Square Error:RMSE)是用来评价算法性能的重要指标。实验四设定在小快拍L=50场景存在一组空间分布距离较近的远场窄带目标源θ11=20°,θ12=25°,θ13=30°,在不同信噪比下使用文献[7]的FOMP算法、文献[12]算法、Root-MUSIC算法以及本文算法进行DOA估计,所产生的RMSE定义为:
(16)
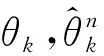
从图5中可以看到,快拍数的不足会会严重影响子空间算法,如Root-MUSIC算法的性能,然而却不会对本文所提算法产生明显的影响,这主要得益于OMP算法的框架。FOMP算法虽然通过扩大字典维数改善了分辨率性能,但是没有从根本上降低冗余字典列间的互相关性,所以在实验条件下得不到无偏估计。本文所以算法在低信噪比时表现略差于其他算法,但是由于本文中基于OMP算法框架的NSVOGOMP算法不需要进行lp,0≤p≤1范数约束的优化求解,存在明显的计算量和实时性优势。
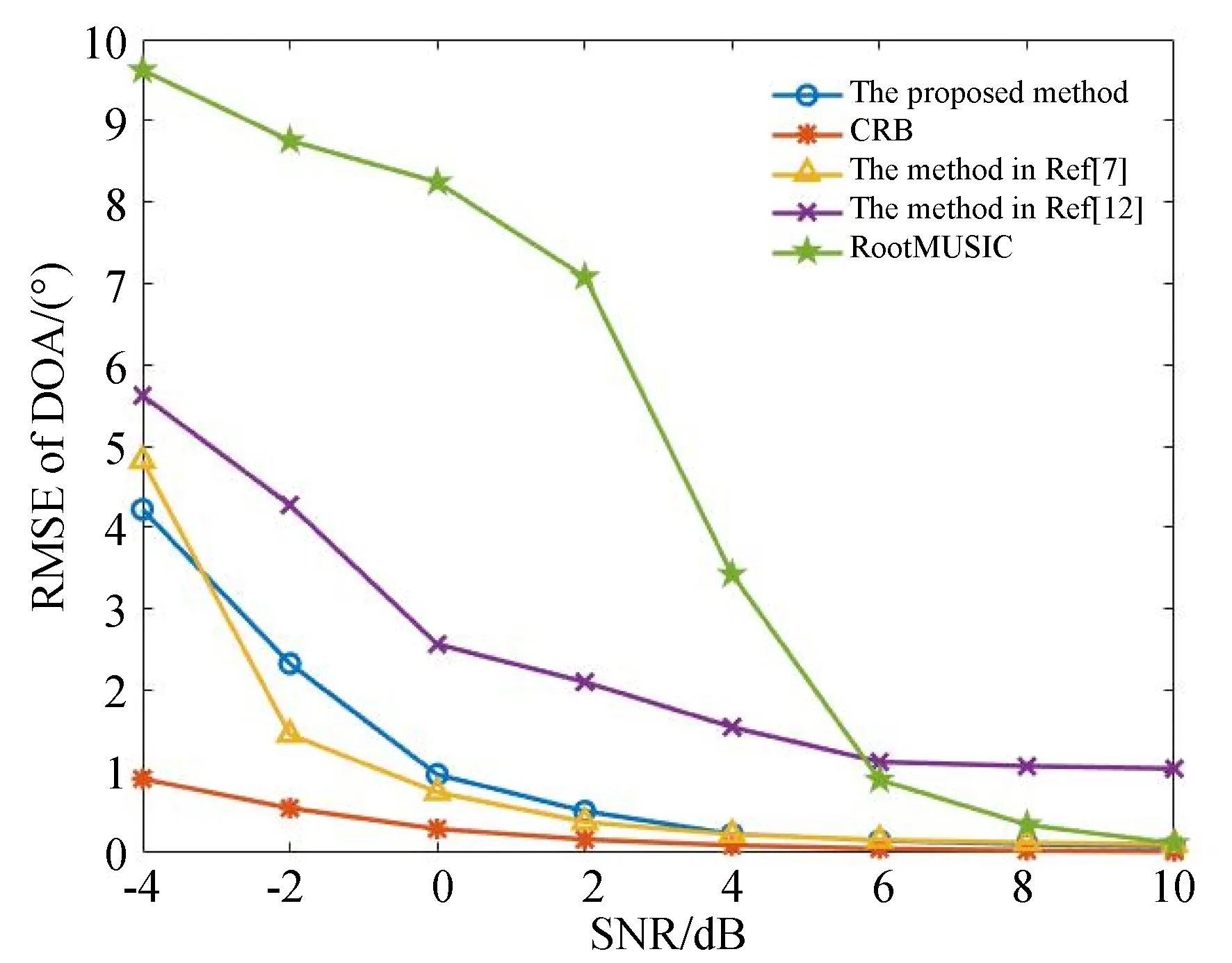
图5 几种算法的RMSEFig.5 RMSE of several algorithms
5 结 论
本文从阵列输出协方差矩阵出发,考虑到DOA角度偏离预设网格时产生的量化误差。在OMP算法框架下设计内部迭代过程对稀疏信号和其相应的量化误差进行联合估计。通过协方差矩阵的最小特征值对应的特征向量构造噪声子空间向量,利用它一方面修正了OMP算法选择支撑集的判定标准,另一方面也对离格误差的估计结果进行判别。与子空间类算法相比,本文所提算法所需快拍数较少且无需预知信源个数;与一般贪婪类算法相比,本文所提算法大幅提高了对空间信号源方向的分辨能力;与lp,0≤p≤1范数优化类算法相比,本文所提算法无需设置正则化参数且计算量较小。

