高分辨率全色遥感图像多级阈值分割
杨 蕴,李 玉,赵泉华
(辽宁工程技术大学 测绘与地理科学学院 遥感科学与应用研究所,辽宁 阜新 123000)
1 引 言
近年来,随着遥感传感器技术的进步,已发射了如Landsat,SPOT,IKONOS,QuickBird和WorldView等卫星,其对地面目标的采样距离和重访周期在不断减小,获得了大量像素大小为十几米到亚米之间的高分辨率全色遥感图像数据[1]。这些数据可以提供同一地区更多的地表详实数据,便于更精确地实现地表观测和地形测量。但高分辨率全色图像包含信息的高复杂性对遥感图像分析方法提出了更高的要求,为了有效利用这些信息,通常将图像分割成一系列同质区域来过滤同一类别地物内部的异质性,因此图像分割是高分辨全色遥感图像分析的第一步和关键步骤[2]。现有全色遥感图像分割方法可大致分为三类:基于区域、边缘和阈值的方法[3]。其中,阈值法是最常用的方法之一,具有简单易行、性能稳定等优点[4]。在该类方法中,精准分割的关键取决于最优阈值的选择,在实际使用中,阈值的选取有多种方法,如直方图法[5]、大津法[4]、最大熵法[6]、模糊聚类法[7]等。其中,最大熵法以其分割效果好、适用范围广等特点,具有广泛的应用前景。
基于最大熵的两级阈值图像分割方法由Kapur等[6]提出,其用穷举法选取使分割后图像熵最大的阈值将图像分为目标和背景两部分。由于真实图像通常包含多个目标,因此提出了如文献[8-10]中的基于最大熵的多级阈值图像分割方法,当图像直方图分布呈现明显双峰或多峰时,其能较好地实现背景和多目标的分离。然而图像往往具有模糊性,造成直方图分布复杂,使得很难获得最优阈值。对此,一些学者将一型模糊集中的隶属度和熵结合,构造了最大模糊熵来量化图像的模糊性。如宋欢欢等[11]提出的基于模糊熵的自适应多阈值图像分割方法,Chakraborty等[12]提出的最大模糊熵阈值法的快速算法。基于最大模糊熵的分割精度有所提高,但由于像素隶属度是一个确定值,其提供的模糊特性不足,使得存在较多类属和决策不确定性的问题[13]。区间二型模糊集是一型模糊集的推广,它将隶属度由固定值变换为一个区间,提供的自由度使得比一型模糊集具有更好的不确定性处理能力。近几年,一些学者已将二型模糊集与熵相结合,用于在文献[14-15]中获得最优阈值,但都限于两级阈值图像分割。本文提出了一种基于区间二型模糊熵的多级图像分割算法,在多级全色遥感图像分割场景中定义区间二型模糊熵,利用一种搜索全局最优值的优化方法对区间二型模糊熵中的参数集进行优化,自动确定全局最优参数组合,从而达到确定最优阈值的同时获得比穷举搜索算法更少的时间开销。
常用的优化算法主要包括遗传算法(Genetic Algorithm, GA)[16]、粒子群算法(Particle Swarm Optimization, PSO)[17]和差分进化算法(Differential Evolution Algorithm, DE)[18]等,它们都是通过群体内个体之间的相互合作与竞争产生的群体智能来指导和优化搜索的方向,但当求解问题复杂时需要较大种群规模,计算量随之变大,不利于求解。同时,随着进化代数的增加,其种群的多样性会变小,过早的收敛到局部最优点,使算法的性能在进化的过程中变差。为了解决上述问题,研究者将量子计算理论与GA相结合,提出了量子遗传算法(Quantum Genetic Algorithm, QGA)[19]。它将潜在的解利用多态量子比特编码为染色体,其在概率上表示所有可能状态的叠加,因此在进化过程中可生成不同状态的个体,能保持解决方案的多样性,由此可克服传统优化算法早熟收敛的问题。同时,量子旋转门的旋转运算,可充分利用当前最佳个体的信息进行下一次搜索以更新个体并避免停滞。与传统优化算法相比,QGA具有种群规模小、种群多样性好、适应性强等优点。
为了提高传统模糊熵的分割精度,同时实现更好的时间性能,本文采用自适应QGA(Adaptive QGA, AQGA)对在多级全色遥感图像分割场景中定义的区间二型模糊熵参数进行自动选择。利用量子比特将模糊参数编码为量子染色体,设置若干量子染色体构成初始模糊参数种群,并以定义的区间二型模糊熵作为评价函数,对种群中的个体进行适应度评价,保留和记录最优个体。利用量子旋转门实现量子染色体向最大适应度方向进化,并根据父代和子代量子染色体的差异和进化代数自适应地调整量子旋转角的大小,以最终进化的种群中适应度最大的个体为最优参数,据此,由最大模糊性原则得到多级阈值,实现高分辨全色遥感图像的最优多级阈值分割。
2 算法描述
2.1 图像的概率划分
设z={z(m,n), (m,n)S}为定义在图像域S、大小为M×N的待分割图像,其中,(m,n)表示像素位置,z(m,n)为像素(m,n)的光谱测度值,z(m,n){0,1,,L-1},L为图像的光谱测度量化级,zmin和zmax分别为图像z的像素光谱测度的最小值和最大值。对于光谱测度为i,i[zmin,zmax]的像素点,其在图像中出现的概率pi为:
pi=ni/M×N,
(1)
其中ni为图像像素光谱测度为i的个数,满足如下关系:
(2)
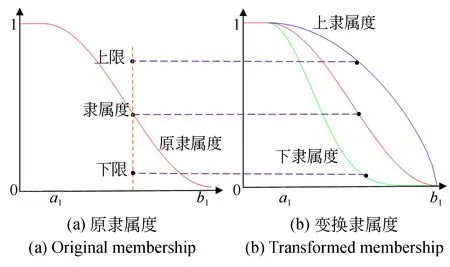
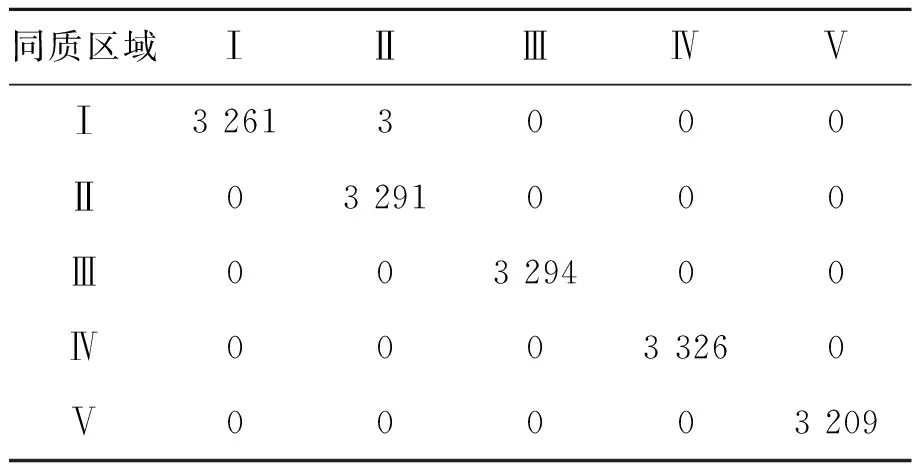
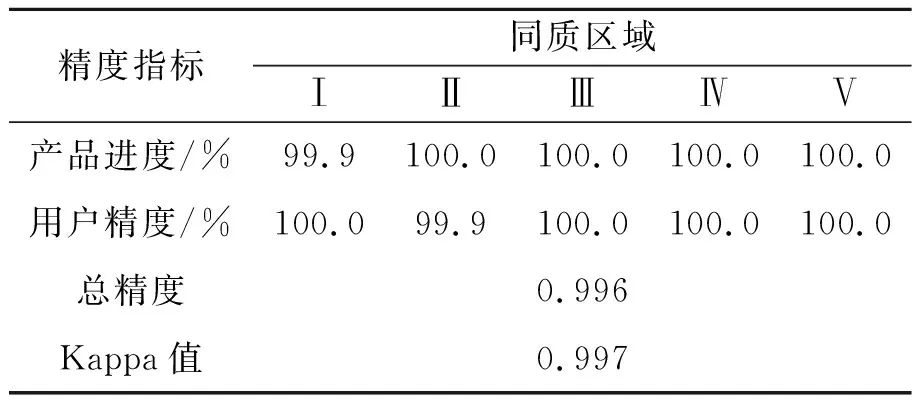
假设T1,T2, ... ,TC为z的C个阈值,满足zmin=T0 因岭型分布隶属函数由升和降两分布组成,因此对图像C级阈值处理,需用C个阈值T1,T2,,TC来估计Sk,k{1,2,,C+1}的隶属度μk,具有2×C个参数,即模糊参数集P={a1,b1,,aC,bC},其中,0≤a1≤b1≤≤aC≤bC≤L-1,如图1所示。 图1 多级岭型隶属函数Fig.1 Multi-level ridge membership function 第k个隶属函数可表示为: (3) 其中,k{1,2,,C+1},a0=b0=0,aC+1=bC+1=L-1。以μk(i)为基,构造区间二型模糊集,可表示为: Fk= (4) 其中:k{1,2,,C+1},2πr和r分别为Fk的上和下隶属函数,其用μk(i)构造,可表示为: (5) 其中,λ>1为指数变化系数,根据经验取λ(1, 5],本文取λ= 3。图2为λ=3时,μ1(i)的降岭型分布变换示意图,原隶属度曲线如图2(a)所示,变换后的隶属度曲线如图2(b)所示。 图2 区间二型模糊隶属度Fig.2 Interval 2 fuzzy membership degree (6) 由像素光谱值及其概率pi,对Sk进行的概率划分,其概率分布为: (7) 其中:k{1,2,,C+1},T0=zmin,TC+1=zmax。则Sk的区间二型模糊熵可定义为: Ek=E(Sk)= (8) 其中:k{1,2,,C+1}。对图像C级阈值处理将图像域S分成C+1个同质区域,因此,对含有C个阈值的区间二型模糊总熵的判别函数可表示为: (9) 以图像的区间二型模糊总熵最大为准则,搜索参数的最佳组合,确定最优参数集P={a1,b1,,aC,bC},使真正代表目标和背景的信息量最大: P*=Argmax(E). (10) 由于模糊集的隶属值越接近0或1,模糊性越小,若越接近0.5,模糊性越大,则按分割区域的最大模糊性原则,可用模糊参数由式(11)的方式获得阈值: (11) QGA在函数寻优方面具有计算量小,收敛速度快等特点,因此本文将AQGA用于式(9)中最优参数组合的确定,以实现图像多级阈值分割。在寻优过程中,包含以下步骤:量子染色体编码,量子染色体测量和解码,适应度评价,量子染色体进化。 2.3.1 量子染色体编码 QGA中的染色体用量子比特(Q-bit)进行编码,一个量子比特可表示|0态和|1态及其之间的任意中间态,可表示为: |ψ〉=α|0〉+β|1〉, (12) 其中,α和β分别是态|0和|1的概率幅,且满足以下归一化条件: (13) 其中,|α|2和|β|2分别表示态|0和态|1的概率幅。 本文的目的是将AQGA作为优化工具,寻求最优参数集P={a1,b1,,aC,bC},以实现图像多级阈值分割。因此对P进行编码。假设第t代种群为,D},其中D是种群规模,代表第t代种群中P的第K个潜在解个体,其在量子染色体的存储和表达如下: (14) (15) 对应的染色体表示为: (16) 则该染色体可分别以概率1/8,3/8,1/8和3/8表示4种状态000,0001,100和101。由此可看出,通过制备不用的概率幅可以使得一条染色体同时描述多种状态,使得潜在解具有多样性,有利于最优解的寻找。 2.3.2 量子染色体测量和解码 (17) 2.3.3 适应度评价 (18) 在最大适应度值所对应的量子染色体中随机选择一条作为进化目标,记为R的第h列的元素,h可表示为: h=round(rand(1)×R), (19) 其中,rand(1)表示生成[0, 1]之间的一个随机数,若rand(1) = 0,取h= 1。 2.3.4 量子染色体进化 本文采用量子旋转门G,其使量子比特在单位圆内发生转动,从而导致相位发生变化,由此增加种群的潜在多样性。记第t代的量子门为G(t),G(t) = {GK(t),K= 1, 2,,D},其中,D为种群规模,,表示第t代第K个染色体的量子门,K{1, 2,,D},{1, 2,, 2ZC}为作用于量子比特的旋转门,可表示为: (20) 其中,φK,q为种群中第K个染色体中第q个量子比特的旋转角,其更新过程如下: (21) 图3 量子旋转门调整量子比特Fig.3 Quantum bits are adjusted by quantum rotation 因此,第t代种群的更新过程可描述为: Q(t+1)=G(t)×Q(t), (22) 其中,G(t)为第t代的量子门,Q(t)和Q(t+ 1)分别为第t代及其进化后第t+ 1代的种群。 (23) 图4为本文方法的流程图,为了更好地理解其中的过程,对流程总结如下。 图4 算法流程图Fig.4 Algorithm flow chart S1 统计待分割图像中各个像素点的光谱测度值,计算光谱测度为i,i[zmin,zmax]的像素点在出现的概率pi,如式(1)所示; S2 以一型模糊集中的多级岭型模糊隶属度函数(见式(3))为基,对原隶属度曲线(见图2)进行变换,构建区间二型模糊集,如式(4)所示; S3 由构造的区间二型模糊集和阈值个数,在多级分割场景中定义模糊熵准则,如式(8)所示; S4 对区间二型模糊总熵(见式(9))的参数集P={a1,b1,,aC,bC}进行编码,初始化种群Q(t),其存储和表达如式(14)所示; S5 对Q(t)中各个个体进行解码为二进制串,得到叠加态的确定解M(t),其基本原理如式(17)所示; S6 将S3定义的总熵准则作为适应度函数(见式(9)),根据适应度大小评价各个个体的优劣,保留适应度最高的个体作为进化目标; S7 判断是否满足结束条件,如果满足则按照当前最大适应度对应的最优参数集合确定多级阈值(见式(11)),否则继续计算; S8 利用第t-1代量子旋转角调整策略(见式(23))更新G(t),并将其作用于Q(t)中的所有个体(见式(21)和式(22)),得到进化后的新种群Q(t+1); S9 对Q(t+1)执行步骤S5,S6和S7,使得各个体向目标方向进化; S10 将算法执行到最大代数或父子代的最大适应度的差值小于0.01,否则返回步骤S7。 本文通过MATLAB r2015b编写程序,其运行环境为Windows7 32位专业版操作系统的,具有4G内存,处理器为Intel(R)Core(TM)CPU 32 G的计算机。为了验证本文提出的区间二型模糊熵方法的可行性,利用文献[8]中基于最大熵的算法和文献[12]中基于一型模糊熵的算法作为对比算法,对其分割结果从目视分析、监督和非监督评价来进行比较分析。同时为了说明本文AQGA的优越性,以本文定义的区间二型模糊熵为目标函数,选择穷举搜索算法(Exhaustive Algorithm, EA)[21],GA,PSO和DE作为搜索对比算法。由于各方法具有相同的目标函数,其分割结果相差不大,因此在论文中不对其分割结果进行展示,从搜索速度、精度和鲁棒性来进行比较分析,其中用EA方法验证对区间二型模糊熵的参数集进行优化的必要性;GA,PSO和DE表明在优化搜索方法中选择本文AQGA的优势。对于各图像的定量评价,由于模拟图像已知参考图像,选择监督评价中应用最广泛的混淆矩阵来计算用户精度、产品精度、总精度和Kappa系数对分割结果进行定量评价。对于遥感图像,利用文献[22]提出的面积加权方差(Area-Weighted Variance, WV)和Jeffries-Matusita(JM)距离对分割结果进行非监督评价。WV用于测量全局分割同质区域内的优度,并按每个同质区域的面积进行加权。其定义如下: (24) 其中:k{1,2,…,C+1}为同质区域索引,C+1是分割的同质区域数,ak为k区域的面积,vk是k区域的方差。较低的WV表明分割结果具有较高的区域内同质性。JM用于测量分割同质区域间的整体优度,并按每个区域的面积进行加权,其定义如下: (25) 其中Jk是波段区域k的JM距离,可表示为: (26) 其中:Lk为区域k的边界长度,Lkb为k与相邻区域b{1, 2, …,}的共同边界长度,Bkb是根据区域邻接图计算区域k和b的巴氏距离,可表示为: (27) 其中,μk,μb和vk,vb分别是相邻区域k和b的均值和方差。较低的JM表明具有较高的区域间异质性。 此外,为了验证本文利用AQGA优化模糊参数集的优势,利用GA,PSO和DE作为对比优化算法,并从寻优时间和最优参数与本文方法进行比较。参考文献中对优化算法参数的描述,为GA,PSO,DE和AQGA设置最佳参数,如表1所示。 表1 GA,PSO,DE和QGA的参数设置 通过尺度为256×256像素的标准灰度图像(见图5(a))对所提方法进行测试,假定其编号为I-V的区域内各像素相互独立,且服从均值和标准差如表2所示的Gaussian分布,生成如图5(b)所示的模拟图像,其光谱测度值的分布如图5(c)所示。 图5 模板图像和模拟图像Fig.5 Template and simulated images 表2 模拟图像的Gaussian分布参数 以图5(b)为输入,利用AQGA寻优构造的多级区间二型模糊熵参数,得到最优参数集P={8, 76, 79, 114, 118, 152, 167, 202}。由此根据式(9)得到分割区域的总熵E(P)=6.56,根据式(11)定义的方式得到阈值T={42,96.5,135,184.5}。与表2的标准数据和图5(c)相比,得到的T在各区域均值间,可满足最佳分割要求。以T对图5(b)进行分割,结果如图6(a)所示。为了从视觉上评估所提方法的精度,将分割结果的轮廓线(见图6(b))与原始图像叠加,如图6(c)所示。 由各区域参数(见表3)和图6的结果可以看出,尽管区域间的均值(如Ⅱ和Ⅲ)和标准差(如Ⅰ和Ⅴ)较相近,本文方法仍能够对其分割出来,具有较好的视觉效果。 图6 模拟图像实验结果Fig.6 Experimental results of simulated images 为了对分割结果精度进行统计分析,以图5(a)为标准分割数据,计算与分割结果的混淆矩阵[23],如表3所示。 表3 分割结果的混淆矩阵 据此分别计算出产品精度、用户精度、总体精度和Kappa值,如表4所示,其中各项指标越高,表明其分割精度越高。 表4 产品、用户、总精度和Kappa值 从表4可以看出,各区域的产品精度和用户精度均达到较大值,总精度和Kappa值也达到0.99以上,一般分类器Kappa值达到0.8以上就是优质分类器[24],因此表明本文方法的有效性和准确性。 选取4幅具有不同地物的高分辨全色遥感图像,如图7(a)~(d)所示。其中,图7(a)是分辨率为2.5 m,尺度为370 pixel×370 pixel的CARTOSAT-1农田图像,人为判读含有道路、农田和裸地3类;图7(b)是分辨率为0.5 m,尺度为500 pixel×500 pixel的Worldview-1码头图像,人为判读含有水体、房屋、道路、裸地和植被5类;图7(c)是分辨率为0.7 m,尺度为435 pixel×435 pixel的房屋图像,人为判读含有房屋、道路和操场等5类,图7(d)是分辨率为0.5 m,尺度为600 pixel×600 pixel的海岸图像,人为判读含有房屋、栈道道路和沙滩等7类。各图像光谱测度值的分布如图8所示,从原始图像和其直方图的对比可以看出,直方图的峰谷数与图像中同质区域数并不一致,使得仅基于直方图的分割方法失效。 图7 全色遥感图像Fig.7 Panchromatic remote sensing images 图8 全色遥感图像的直方图Fig.8 Histogram of panchromatic remote sensing image 以图像统计直方图中各像素光谱测度值出现的个数为输入,区间二型模糊熵最大为准则,通过本文方法寻优最佳阈值组合,结果如表5所示。以表中阈值组合和对比算法对图7的全色遥感图像进行分割实验,其中,图9(a1)~(d1)、图9(a2)~(d2)和图9(a3)~(d3)分别为采用文献[8]、文献[12]和本文方法所得的分割结果。由对比可以看出,传统最大熵法在目标和背景光谱测度相差较小时,易导致误分割现象,使得如图9(c1)的操场和图9(d1)的沙滩内部含有较多的分割噪声。模糊熵法将隶属度和熵相结合来量化图像的模糊性,其对分割结果的精度都有一定程度的提升,但由于使用的是一型模糊集,像素隶属度是一个确定值,因此提供的模糊特性不足,使得对如图9(c2)和9(d2)的目标区域有较多欠分割现象,精度仍需要提高。本文方法利用二型模糊集构建模糊熵,每个像素点隶属度是一个函数,其可提供较大的自由度来更好地处理不确定性,这在一定程度上减少了同质区域内部的分割噪声。 图9 分割结果Fig.9 Segmentation results 表5 最佳阈值组合和最大熵值 表6利用WV和JM对不同方法进行非监督评价的结果。从表中可以看出,本文方法在WV和JM方面均具有较小的值,说明本文方法相较于对比算法,分割结果的同质区域内部具有较小的差异程度,且各同质区域面积较为完整,相邻同质区域间紧密相连,具有较大公共边界,满足图像分割结果对空间连续且光谱均匀的要求。 表6 遥感图像分割评价指标 为了能更加直观观察算法对评价指标的降低幅度,以表6中指标较大的文献[8]的方法作为评价标准,计算文献[12]和本文方法的定量评价指标降低幅度,如表7所示。其中,M0和J0为文献[8]结果的MV和JM;M和J为文献[12]和本文方法的MV和JM。由表中数据可看出,本文算法的两个质量指标都得到较大的降低,MV平均降低提升了39.7%,JM平均降低了14.7%,表明了本文方法有较好性能,满足算法鲁棒性的要求。 表7 定量评价指标的降低幅度 以本文的区间二型模糊熵为目标函数,分别利用EA,GA,PSO,DE和本文AQGA对图7(a)~(d)分割的模糊参数集进行优化,各算法的收敛曲线如图10所示,其中各收敛图的横纵坐标分别为迭代次数和适应度值(区间二型模糊熵)。从图10可以看出,本文AQGA相比其他三种算法,在收敛速度和全局收敛能力方面都具有一定的优越性。为了更客观地评价算法的性能,对各算法运行20次的时间、精度和鲁棒性进行比较,如表8所示,其中对应于以秒为单位的平均时间hm(s),以比特/像素为单位的平均最佳目标函数值fm及其标准差std。 图10 算法收敛曲线Fig.10 Algorithms convergence curve 表8 EA,GA,PSO,DE和AQGA的平均性能 由表8的对比可以看出,EA由于需要依次遍历所有的元素,并判断是否为可行解,因此用时较长,GA,PSO,DE和本文AQGA并不机械的检查每一种情况,减少了搜索量,耗时相应减少。相比之下,AQGA的平均耗时最少,PSO与DE几乎相同,GA耗时相对较多,对fm和std,AQGA对于所有图像取得最大的fm和最小的std,这表明AQGA不仅能更好地优化问题,同时具有更强的鲁棒性。 模糊熵法具有良好的性能,是一种主要的图像阈值分割方法,但存在模糊特性不足、计算量大、自动性差等问题,使其在实际应用中受到限制。为了提高分割精度,本文利用岭型模糊隶属度函数构造的区间二型模糊集上定义图像区间二型模糊熵,以增加其模糊特性,同时为了实现更好的时间性能,将自适应量子遗传算法引入到区间二型模糊熵多级阈值图像分割中,将其作为区间二型模糊熵中模糊参数集的优化工具,从而快速精确地确定图像的多级阈值,实现图像最优多级图像阈值分割。通过对含有不同地物的高分辨率全色遥感图像的实验表明:与基于最大熵和模糊熵的方法相比,本文方法能在减少计算时间的同时获得更好的分割结果,面积加权方差可降低39.7%,Jeffries-Matusita距离可降低14.7%,运行时间秒6.403 s。基本满足高分辨全色遥感图像分割结果对空间连续且光谱均匀的要求且具有较高的实时性。 对高分辨率全色图像分割而言,由于地物种类繁多、背景环境复杂和实地考察困难等原因,造成人为确定其类别数比较困难。因此,在未来工作中,将对此问题进行研究,实现高分辨率全色遥感图像的可变类分割。2.2 多级区间二型模糊熵

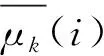
2.3 基于AQGA的区间二型模糊熵算法

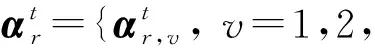
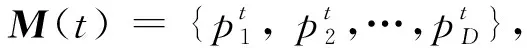
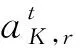
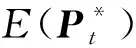
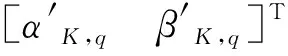
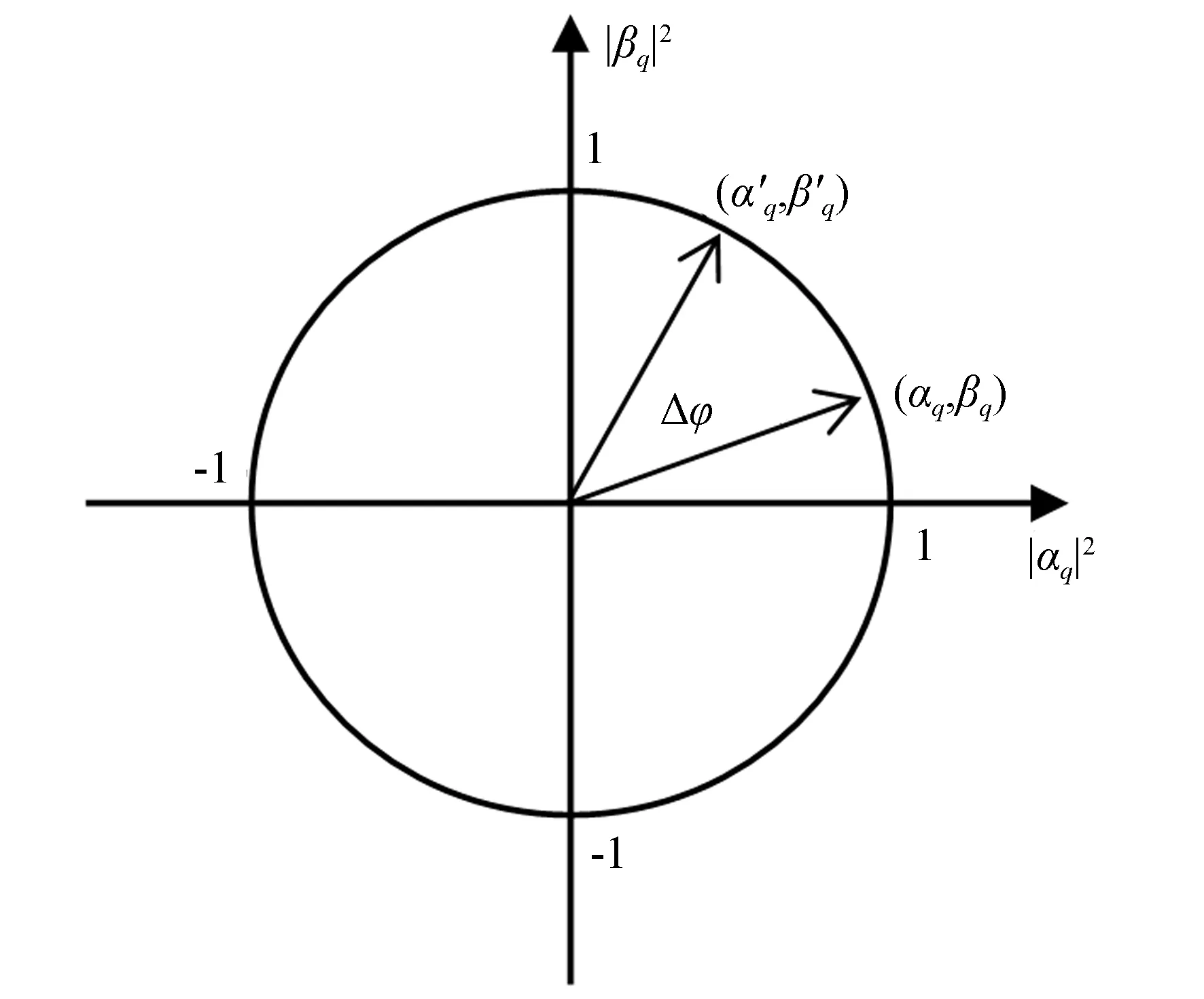
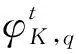

2.4 算法流程

3 实验结果与讨论
3.1 实验设置

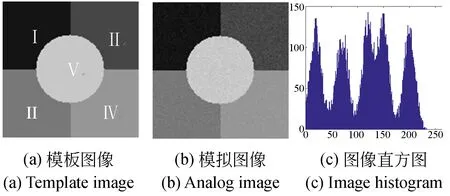
3.2 模拟图像分割


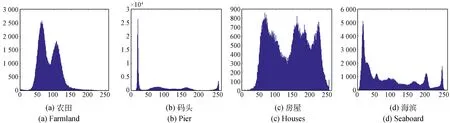
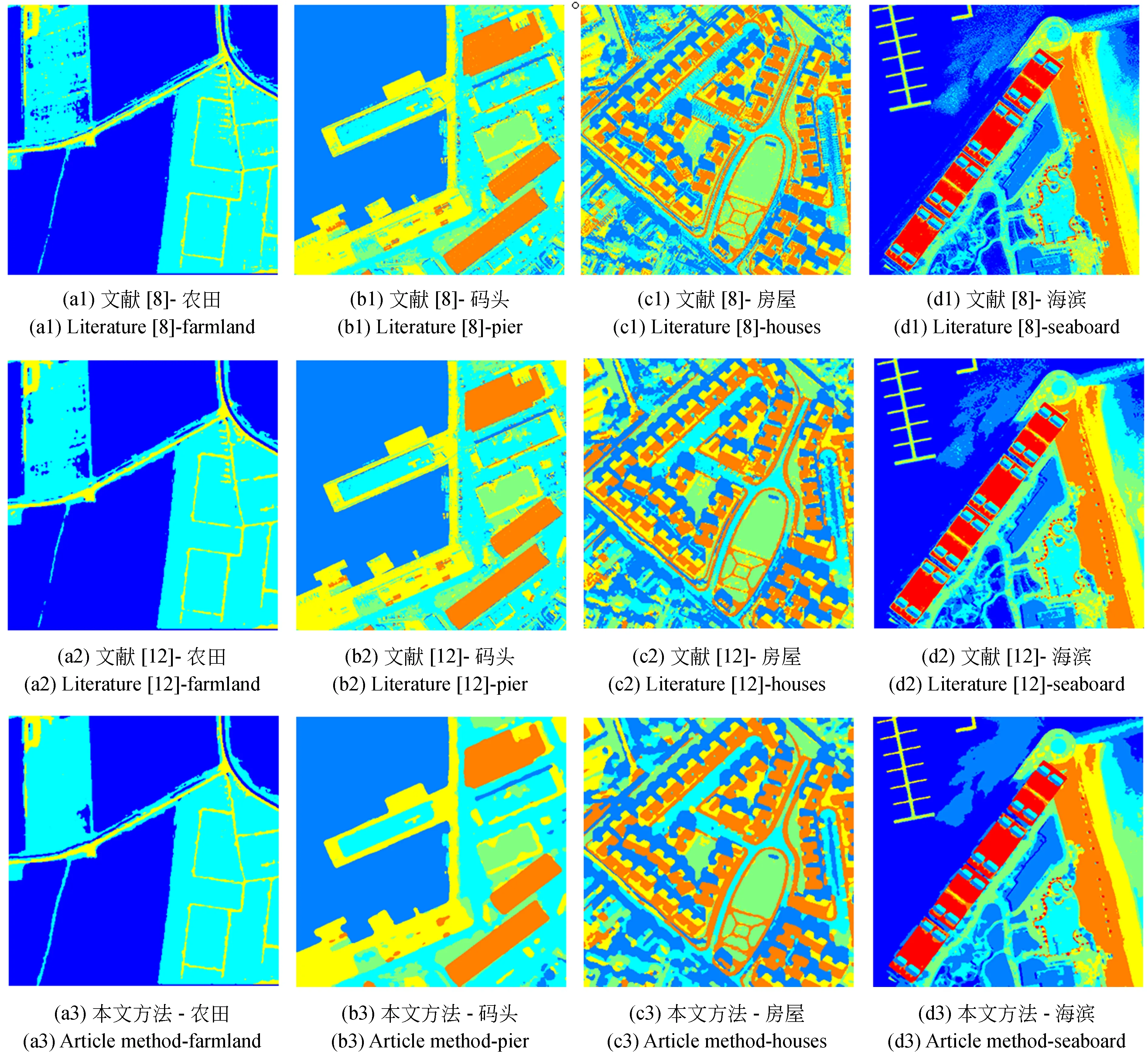
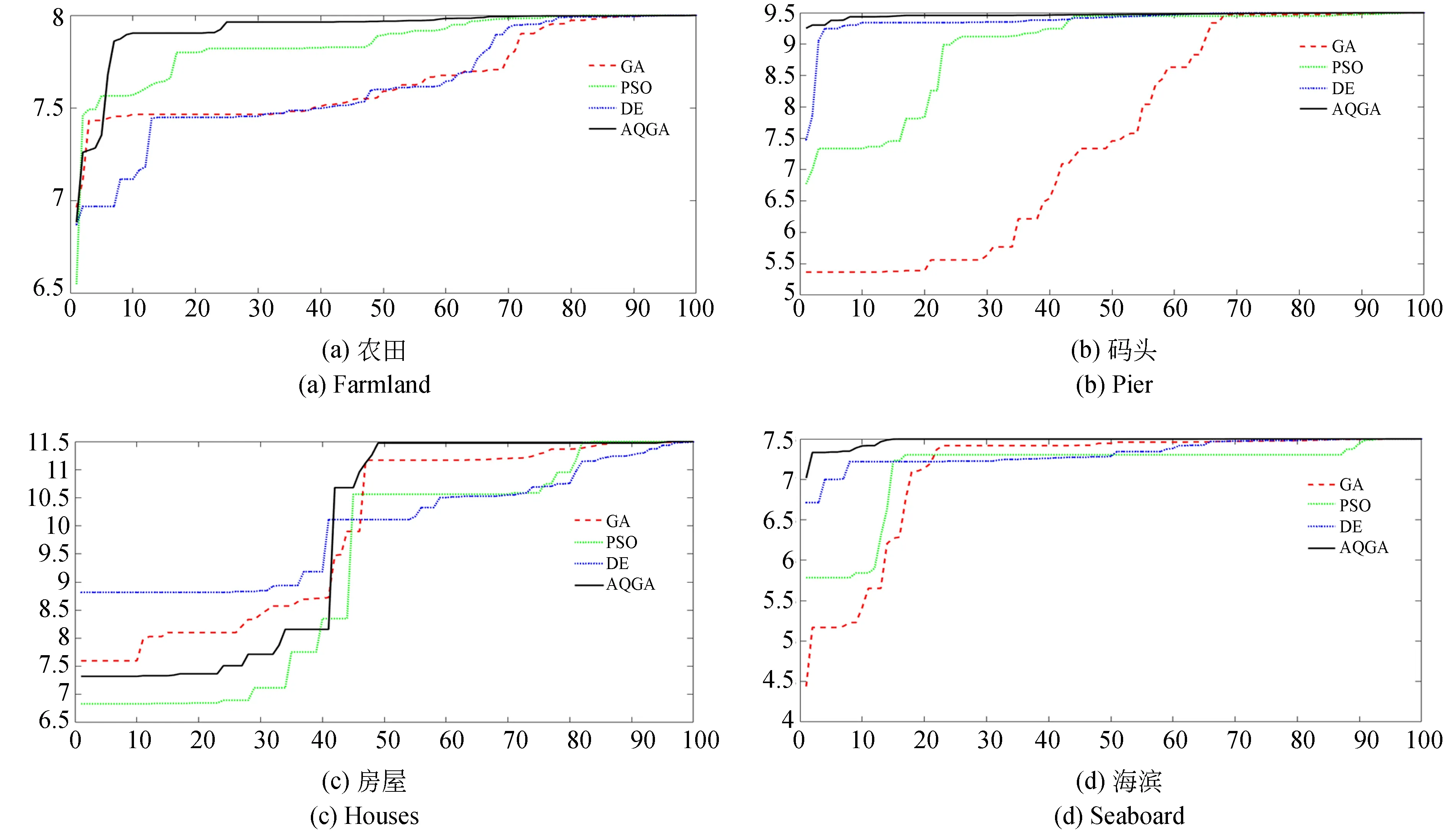
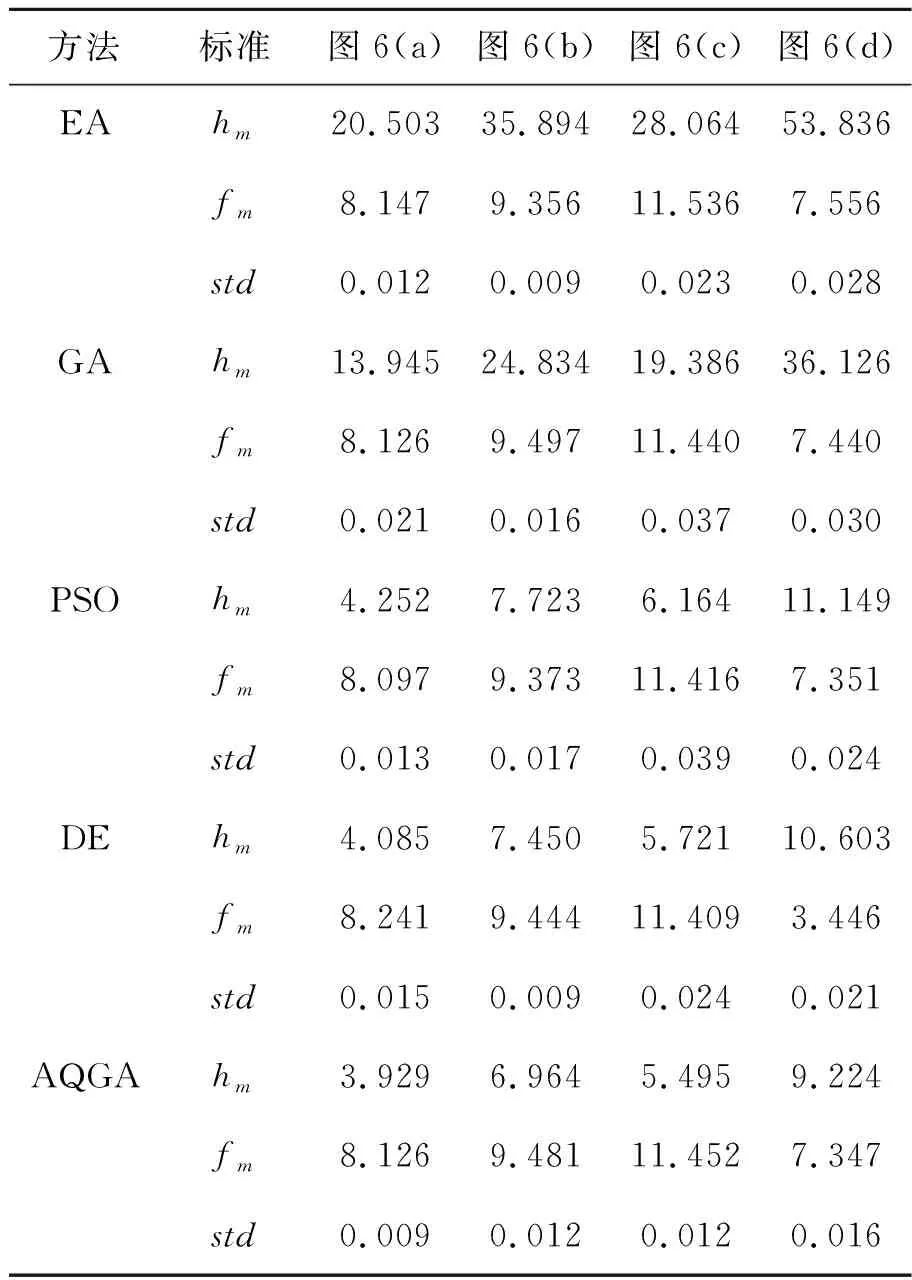
3.3 遥感图像分割




4 结 论

