空间光调制器像素结构对波前重建的影响

肖昭贤，温金鹏，赵自新，樊 晨

(1.中国工程物理研究院 总体工程研究所，四川 绵阳 621999；2.西安交通大学 机械工程学院机械制造系统国家重点实验室，陕西 西安 710049)

1 引 言

液晶空间光调制器(Liquid Crystal Spatial Light Modulator ,LC-SLM)[1]是由在空间上二维阵列排布的独立单元构成，基于液晶的电控双折射原理，它可以在光信号或电信号随时间和空间变化的驱动和控制下，对光波的振幅、相位、波长、偏振态和相干性进行调制，是在光逻辑运算、光互联、实时光学信息处理等系统中的关键器件[2]。LC-SLM 具有空间分辨率高、可编程控制、质量轻等优点[3]，在材料的显微处理[4]、全息三维成像[5-6]、空间光束整形和脉冲整形[7-8]、波前传感器[9]及自适应光学[10]等领域有着广泛应用。

在传统的计算全息(Computer-generated Holography,CGH)补偿检测中，非球面与计算全息实体具有一一对应关系，应用通用性较差，而且制造工艺程序复杂、成本高、周期长。科研人员尝试利用LC-SLM对光波相位近似连续调制的能力，作为 CGH 的记录介质，从而实现光学非球面元件的动态计算全息补偿检测。

南京理工大学的朱日宏教授等人[11-12]自2004 年起提出使用液晶电视实时测量非球面的方法，探究了液晶电视的光学性质及它应用于非球面检测的可行性。西安工业大学韩军等人[13-15]利用 LC-SLM 重建波面的PV值为0.420 3λ，RMS值为0.091 4λ。哈尔滨理工大学的周昊[16]基于LC-SLM搭建泰曼格林型干涉光路，对口径为50 mm和 52 mm的两个凹抛物面镜进行了检测，证明了 LC-SLM 作为 CGH 记录介质实时动态灵活测量非球面方法的可行性。2019 年国防科技大学[17]提出了一种使用 LC-SLM 作为可重新配置波前形状的多级干涉图型计算机生成全息图(ICGH)的方法，对非球面和自由曲面进行动态零位测量，提高了测试的灵活性和效率。

非球面动态检测的精度直接取决于LC-SLM波前重构的精度。目前，制约LC-SLM取代实体记录介质，实现高精度波前调控的主要因素包括LC-SLM的像素结构因素、液晶分子响应的自身非线性以及基底空间的不一致性。中科院上海光机所刘世杰等人[18-20]基于菲涅耳衍射原理以及离散傅里叶变换算法,重点分析了像素结构因素的影响，精确地仿真波面经SLM 调制并传播到待测表面的过程,从而获得待测元件处补偿波面误差。在此基础上，本文使用德国 LightTrans 公司研发的物理光学数值分析软件 VirtualLabTM中LC-SLM模块对像素尺寸、填充因子比例及灰度等级对补偿波面的重建精度进行了研究，通过理论分析获得了算法本底误差及多因素耦合误差，从而建立了LC-SLM高精度波前重建的前提条件。

2 仿真原理及模型

利用SLM动态检测非球面的基本原理如下：SLM作为CGH的记录介质，平面波入射至SLM靶面，经调制产生被测光学面的补偿波面。调制函数也就是计算全息图，传统的计算全息图是被相位刻蚀在实体介质上，而SLM则是通过液晶分子偏转，实现离散相位编码输出。

假定被测光学镜面为球面镜，那么理想的补偿波面为：

(1)

由文献[16]可知，补偿波面逆向传播距离为z时，通过光线追迹此平面内波前的理想相位分布为：

(2)

该相位分布即是计算全息图相位，被包裹调制在[-π,π]后，编码加载至SLM上。图1(a)为VirtualLabTM软件中构建的波前重建系统光学系统3D视图，图1(b)为SLM波前重构及检测系统光学流程。

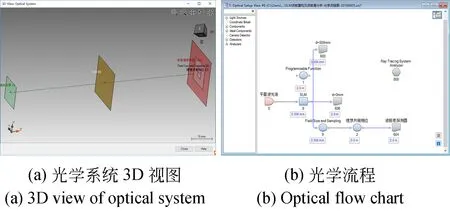
图1 VirtualLabTM仿真Fig.1 VirtualLabTM simulation

SLM上的初始光场为U(x,y)=Aeiφ(x,y)，其中φ(x,y)即为公式(2)所表示的相位分布。光场进行菲涅尔正向传输，光场分布为：

(3)

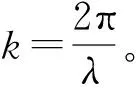
获得复振幅U(u,v)=A′eiφ(u,v)，提取其相位分布φ(u,v)。虽然菲涅尔传输算法本身存在固有计算误差，但在满足采样定理的前提下，φ(u,v)极限接近于φ(x,y)。

实体SLM由大量像素独立单元构成，具有一定的尺寸、填充因子比例及电子器件固有的灰阶量化级次。前两项可直接通过设置参数实现；而灰阶量化级次采用Hard Quantization方法，其表达式如下：

φ(x,y)′=

(4)

其中Q为量化级次，Round[]为取整符号。

像素结构因素被调制叠加到连续相位中，获得实际的相位分布φ(x,y)′，如图2所示。经菲涅尔正向传输，提取实际的补偿波面相位分布φ(u,v)′。实际补偿波面光场A′eiφ(u,v)′通过与理想共轭光场A′e-iφ(u,v)相乘，提取相位误差，得到：

图2 仿真系统叠加像素结构后实际相位分布Fig.2 Phase distribution of simulation system after superposing pixel structure

φerror(u,v)=φ(u,v)′-φ(u,v).

(5)

分别用PV(φerror)/λ(Peak-to-Valley of Wavefront Error /λ)和RMS(φerror)/λ(RMS of Wavefront Error/λ)值表征相位误差。

3 仿真结果

明确仿真系统中传输距离z=500 mm，使用红光波长λ=632.8 nm，理想球面波半径r=100 mm。

3.1 系统原始误差

实体介质计算全息可以是连续的，但是使用数字仿真技术，即使是理想的波前相位分布也会被数字化离散。同时菲涅尔算法中使用离散傅里叶变换，空域的采样间距、空域有限的采样范围以及频域的采样间距都会给计算结果带来误差[21]。经过光场传输，携带算法本身以及数字离散引起的误差，生成存在系统原始误差的理想补偿波面。通过理想补偿波面光场与其共轭光场相乘，提取相位获得系统原始误差，结果如图3所示。

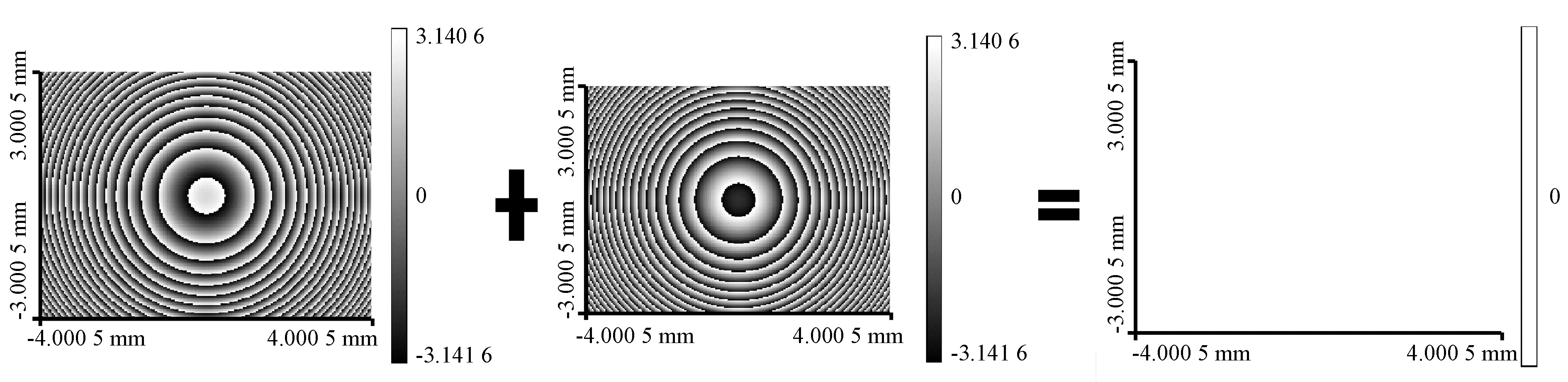
图3 8 mm×6 mm靶面系统原始误差计算示意图Fig.3 Original error calculation diagram of 8 mm×6 mm target system

在计算系统原始误差时，设计的像素尺寸为1 μm。从图3可以看出，8 mm×6 mm靶面尺寸系统补偿波面的原始误差振幅部分处处相等，相位结果近似于零。从表1可知：靶面尺寸越小，系统原始误差反而越大；当靶面尺寸大于8 mm×6 mm时，系统原始误差几乎不变。因此，本文在SLM靶面尺寸为8 mm×6 mm的条件下开展仿真工作，同时忽略由仿真系统引入的原始误差。

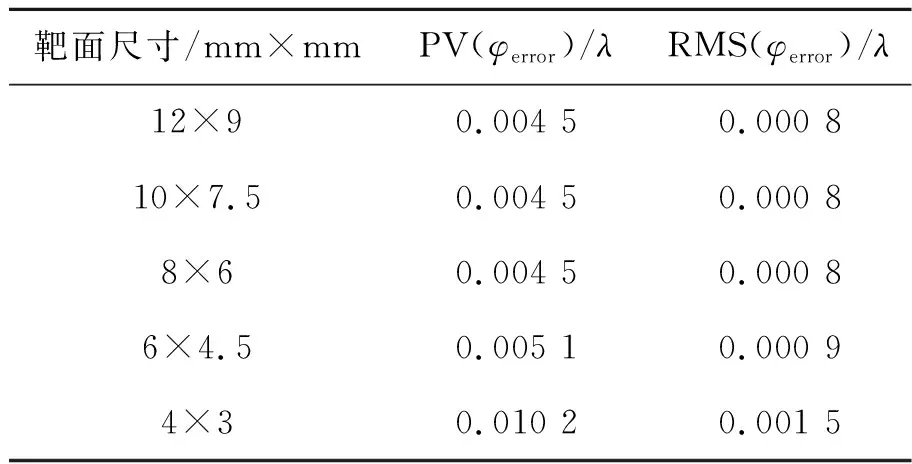
表1 SLM不同靶面尺寸对应的系统原始误差Tab.1 Original errors of SLM system with different target sizes

3.2 像素结构因素误差

目前，同类相位型空间光调制器最小的像素尺寸可达3.74 μm，但价格高昂，因此在光学工程领域常用的SLM像素尺寸仍不小于6 μm。仿真过程中，设定像素尺寸分别为8，10，12，14，16，18，20，25，30 μm，设定填充因子比例分别为40%，50%，60%，70%，80%，90%，100%，设定灰阶量化级次分别为24，25，26，27，28。在VirtuaLabTM软件中搭建仿真系统并进行扫描计算，获得补偿波面误差的PV和RMS值，分别如图4和图5所示。

设定灰阶量化级次为28，补偿波面误差PV值随像素尺寸的变化情况图4(a)所示，图中每一条曲线对应SLM不同填充因子比例，图4(b)则表示补偿波面误差的RMS值。可以看出，不论是补偿波面误差的PV值还是RMS值，在总体趋势上均是随像素尺寸增大而增大，当像素尺寸小于20 μm时，PV值为0.03λ～0.05λ，RMS值为0.005λ～0.007λ，均能满足高精度补偿波前的要求，且填充因子比例对补偿波面误差的影响较小；但是，像素尺寸一旦超过20 μm，PV值和RMS值开始显著增大，并且填充因子比例不同曲线的增长斜率也不同，也就是填充因子比例越低，补偿波面误差增长得越快。

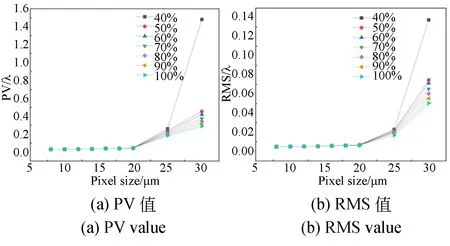
图4 灰阶量化级次为28，补偿波面误差的PV值和RMS值Fig.4 PV and root mean square values of compensating wave surface error with gray-level number of 28

设定填充因子比例为100%，补偿波面误差PV值随像素尺寸的变化情况如图5(a)所示，图中每一条曲线对应SLM不同灰阶量化级次，图5(b)则表示补偿波面误差的RMS值。可以看出，不论是补偿波面误差的PV值还是RMS值，在总体趋势上均是随像素尺寸的增大而增大，和图4(a)、4(b)相似的地方仍然是20 μm存在增长拐点，区别在于像素尺寸小于20 μm时，灰阶量化级次对补偿波面误差的影响已经相对明显。不难理解，离散级次会直接影响着波前调控精度。

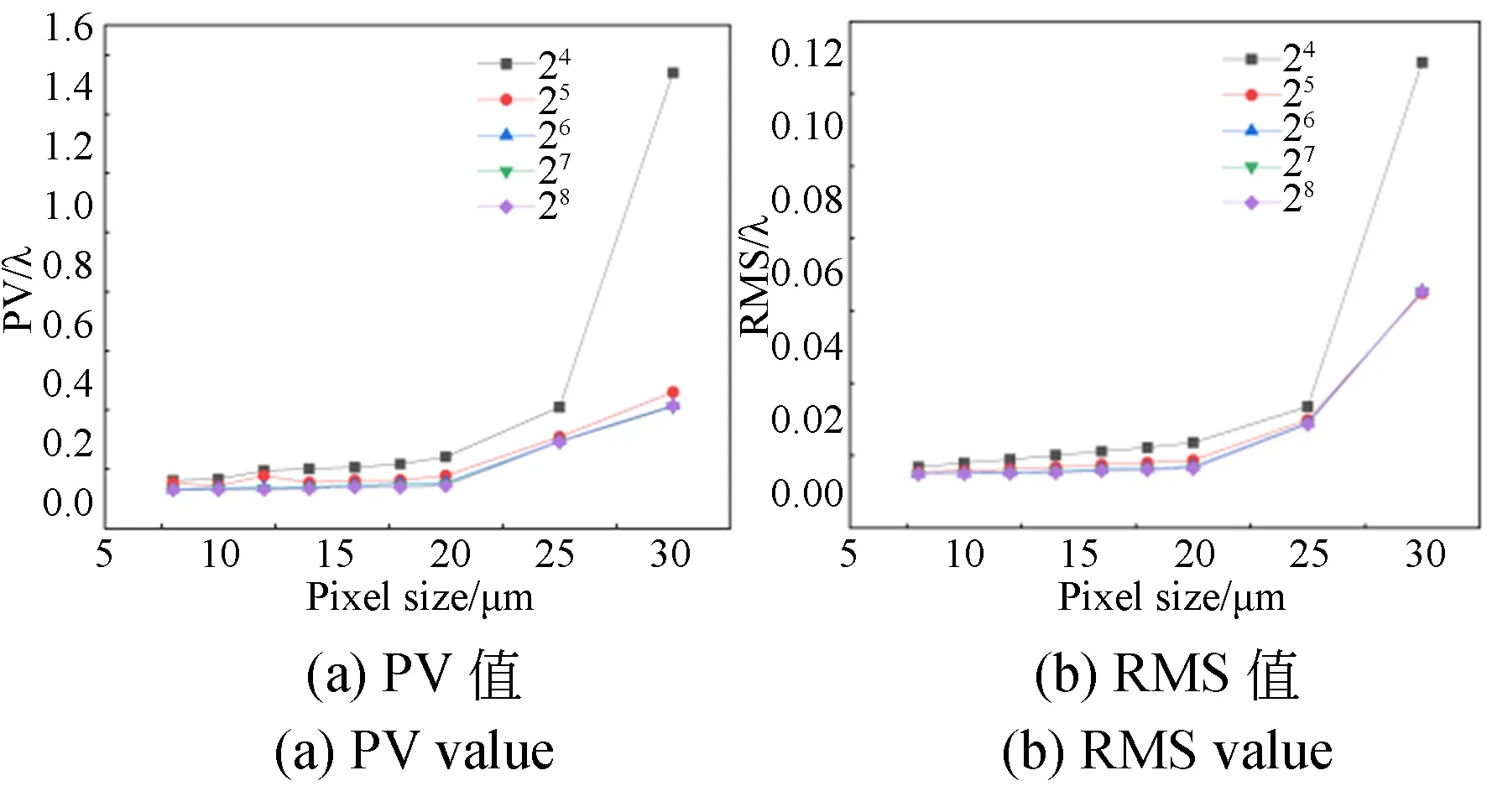
图5 填充因子比例为100%，补偿波面误差的PV值和RMS值Fig.5 PV and RMS values of compensating wave surface errorr with filling factor ratio of 100%

4 分析与讨论

由上文的仿真结果可知，补偿波面误差随像素尺寸的变化存在“拐点”。本文中仿真的SLM像素尺寸为8 mm×6 mm，对于球面波而言，式(2)中的φ(x,y)加载到SLM调制全息图的口径即为D=8 mm。不难得到，这类对称相位分布的最大空间频率位于边缘处。首先获得φ(x,y)的微分函数，公式如下：

(6)

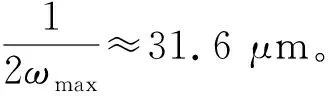
本文补充计算了像素尺寸为48 μm时的补偿波面误差，设定填充因子比例为100%，量化灰度级次为28，计算误差的PV值和RMS值，结果如表2所示。像素尺寸为48 μm时，对应的采样倍数仅为1.32。从表中看出，在满足采样定理的条件下，随着采样倍数的增加，补偿波面的精度也在提高；当采样倍数大于3时，精度趋于一个缓慢增加的过程，此时已能够满足高精度测量的要求。而在不满足采样定理的情况下，补偿波面误差PV值和RMS值急剧增长，可见决定补偿波面误差真正的“拐点”，出现在满足理论奈奎斯特采样频率对应的空间分辨率。

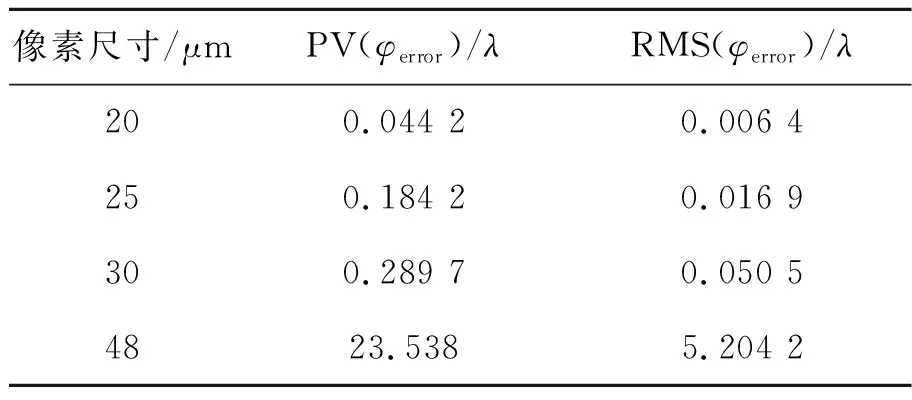
表2 不同像素尺寸对应的补偿波面误差

在满足以上条件的基础上，填充因子比例及灰阶量化级次的影响并不显著，不作为决定性因素。那么，只要计算出被测光学曲面的最大空间频率，适当提高采样倍数，例如3倍，就能选择出合适特性参数的SLM以实现高精度动态测量。这种方法可以有效降低成本，不盲目追求像素尺寸小、填充因子比例高、灰度量化级次高的调制器件。

5 结 论

本文基于菲涅耳衍射原理以及离散傅里叶变换算法,使用物理光场数值分析软件 VirtualLabTM对LC-SLM重建补偿波面精度进行了系统研究，获得了像素结构因素的理论算法本底误差及多因素耦合误差。针对主要由像素采样尺寸带来的误差“拐点”问题，结合重建波面空间频率，提出在满足奈奎斯特定理的基础上，根据被测波面最大空间频率恰当选择符合特性参数的LC-SLM，可降低构建曲面动态检测系统的成本。而且，有赖于电子刻束和微纳制造技术的发展，液晶空间光调制器的像元尺寸完全能够提供一个高精度动态测量的基本条件。由于空间频率的限制，如何提高LC-SLM的动态调制范围是接下来非常重要的研究方向，后续工作更应该关注液晶分子响应的自身非线性以及基底空间不一致性带来的调控误差。