大功率长焦深高斯光束整形设计
李党娟, 王佳超, 陈 阳, 杨金亮, 吴新宇, 苏俊宏*
(1. 西安工业大学 光电工程学院, 陕西 西安 710021;2. 西安高斯激光科技有限公司, 陕西 西安 710032)
1 引 言
大功率激光设备随着现代工业的发展得到了广泛应用,比如激光切割、激光清洗、激光增材等[1-3]。为了使大功率高斯激光激光束在其辐射面积内达到能量密度均匀,且输出光斑达到近似矩形光,需要对耦合输出的高斯光束进行整形。
夏国才等对用于实现激光高效率加工的光束空域整形和时域整形技术进行了详细的分析[4]。余金清等提出利用微透镜阵列与长焦深菲涅尔透镜相结合的办法,实现激光在三维空间的均匀分布,在获得高均匀度的同时极大地延长了其工作深度[5]。邱基斯等基于数字微镜器件(DMD)对高斯光束进行了两次光束空间整形,光束近场调制度由一次整形后的1.85∶1下降到1.33∶1,能量损耗为35.70%[6]。而大功率激光器则需要长工作焦距、耐激光损伤、输出光斑能量均匀且呈矩形光斑的光学系统。
本文通过对系统模型与平顶光束物理模型进行对比,选出合适的光学系统结构;采用ZEMAX光学软件对系统进行仿真优化,得到系统的结构参数和非曲面的面形参数,检验系统结果;计算平顶光束在不同出射距离处的能量均匀度,进而判断系统的工作焦深;最后,通过实验来验证设计效果。
2 整形系统模型选择
常见的高斯光束整形系统模型包括:光阑整形系统、微透镜阵列整形系统、非球面透镜系统和衍射光学元件整形系统等[4,7]。其中,光阑整形系统是人们最开始使用的光束整形系统,它用光阑从入射激光束中提取出所需求的光场分布,其缺点是能量损失严重[8]。Frieden提出的非球面透镜组整形系统,利用多普勒型或伽利略型整形系统,都容易产生严重的波前畸变[9];另外,采用微透镜阵列整形系统,对入射光束光强度不敏感,一般应用于光场强度分布不规则、相干性较差的准分子激光器的整形,以及半导体激光器、发光二极管等多种光源场景下的整形[10]。液晶空间光调制器可实现对不同波长的激光束整形,可以动态改变激光束的光强分布[11]。衍射光学元件整形系统虽然体积小、质量轻,可以将出射光斑整形成任意形状,但是其设计复杂,且加工精度很难达到[12]。
为减小大功率激光整形系统的复杂度,提高工作焦深和激光能量分布均匀度,这里拟采用伽利略式非球面透镜整形系统并进行参数优化。
3 平顶光物理模型及映射函数
简单的平顶光束物理模型为圆域函数,它虽然具有形式简单的优点,但仅能描述平顶光能量均匀分布的特性,而不适合计算平顶光的传输特性。相较于其他平顶光物理模型,平顶洛伦兹模型的计算最为简便,因此为了减少计算量,本文选取平顶洛伦兹模型为平顶光物理模型。
设入射光光强为Iin,出射光光强为Iout,入射面上任意一条光线的投射高度为r1,出射面上与之对应的投射高度为r2,高斯光束的束腰半径为ω0,平顶光半径为R0。z1(r)与z2(r)为两面非球面的面形函数,具体模型如图1所示。
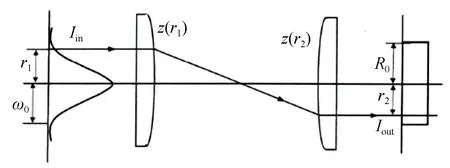
图1 光束整形模型Fig.1 Beam shaping model
由能量守恒定律可知,包含在r1~Δr1与r2~Δr2内的能量相等,在直角坐标系及极坐标系下,可建立下列归一化方程[13-16]:
finput apertureIin(x1,y1)dx1dy1=
foutput apertureIout(x2,y2)dx2dy2=1,
(1)
finput aperture2πIin(r1)r1dr1=
foutput aperture2πIout(r2)r2dr2=1.
(2)
其中高斯光束光强分布表达式为:
(3)
其中RSG和p分别是束腰半径和阶数,ISG,0为归一化光强系数。将式(3)代入归一化方程中,可以计算其归一化光强系数为:
(4)
洛伦兹函数的光强表达式为:
(5)
归一化光强系数IFL,0表达式为:
(6)
将高斯光束和平顶洛伦兹光束函数表达式分别代入方程(2),可以得到映射函数关系为:
(7)
R和r的映射函数关系分别为:
(8)
(9)
特别地,当q→∞时,式(9)可以写为:
(10)
式(10)表明,采用平顶洛伦兹函数作为平顶光束分布函数,其映射函数具有解析解,可为光线追迹提供便利,使得数值计算过程大为简化。
对于伽利略型非球面系统而言,则有:
(11)
4 仿 真
由于传统非球面面形参数方法的计算量大且过程十分繁琐,因此基于光学软件ZEMAX宏语言程序对非球面面形参数进行优化设计,可以大幅减少计算量。
4.1 激光束能量分布整形系统结构及结果
由于开普勒系统具有实焦点,大功率激光聚焦易损坏光学元件,因此选择伽利略型非球面整形系统。依照实际选用激光光源的参数:M因子为1.52,输出平均光功率为500 W,脉冲宽度130~160 ns,重复频率为20~50 kHz,波长为1 064 nm,功率调节范围为10%~100%,选用热膨胀系数小的熔石英材料。通过运行已编好的宏语言得到系统结构参数,如表1所示。
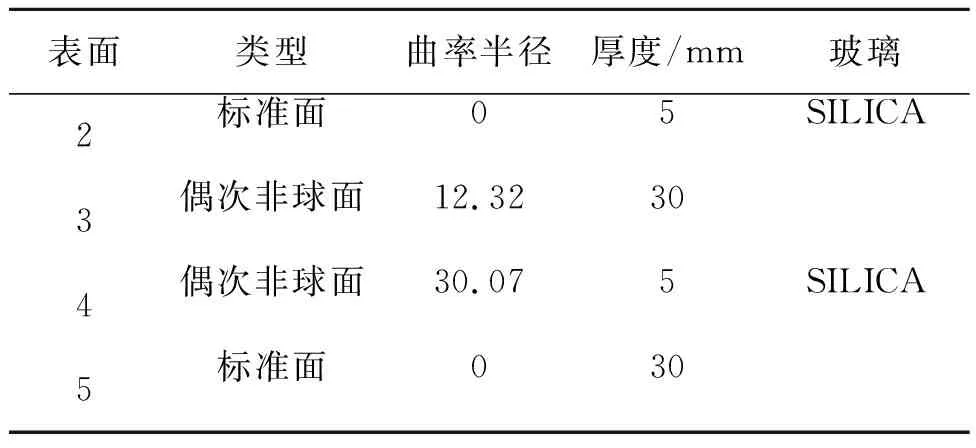
表1 非球面系统的结构参数
为减小加工难度,将非球面面形参数中二次项设为0,非球面面形参数如表2所示。
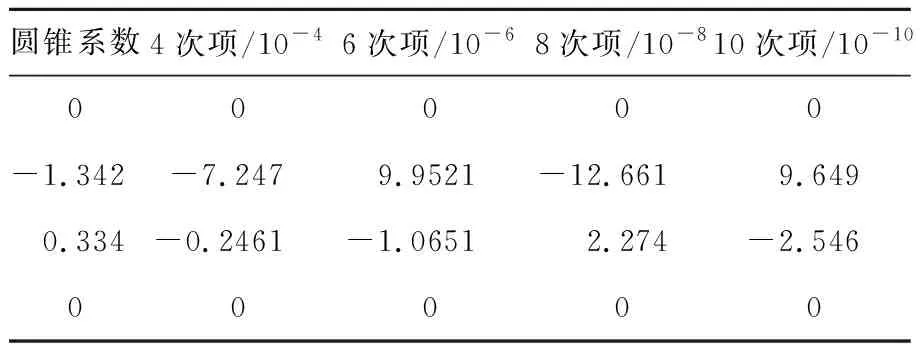
表2 非球面面形参数
伽利略系统的结果如图2、图3和图4所示。其中图2为系统结构平面图;图3为系统入射光X,Y方向的能量分布仿真计算图;图4为系统出射光X,Y方向的能量分布仿真计算图;横坐标代表光斑坐标值,以光斑中心为圆点,纵坐标代表相对照度,单位为W/mm2。由图4可知,激光束经过整形系统后,输出能量分布变为平顶分布,整形效果比较好。
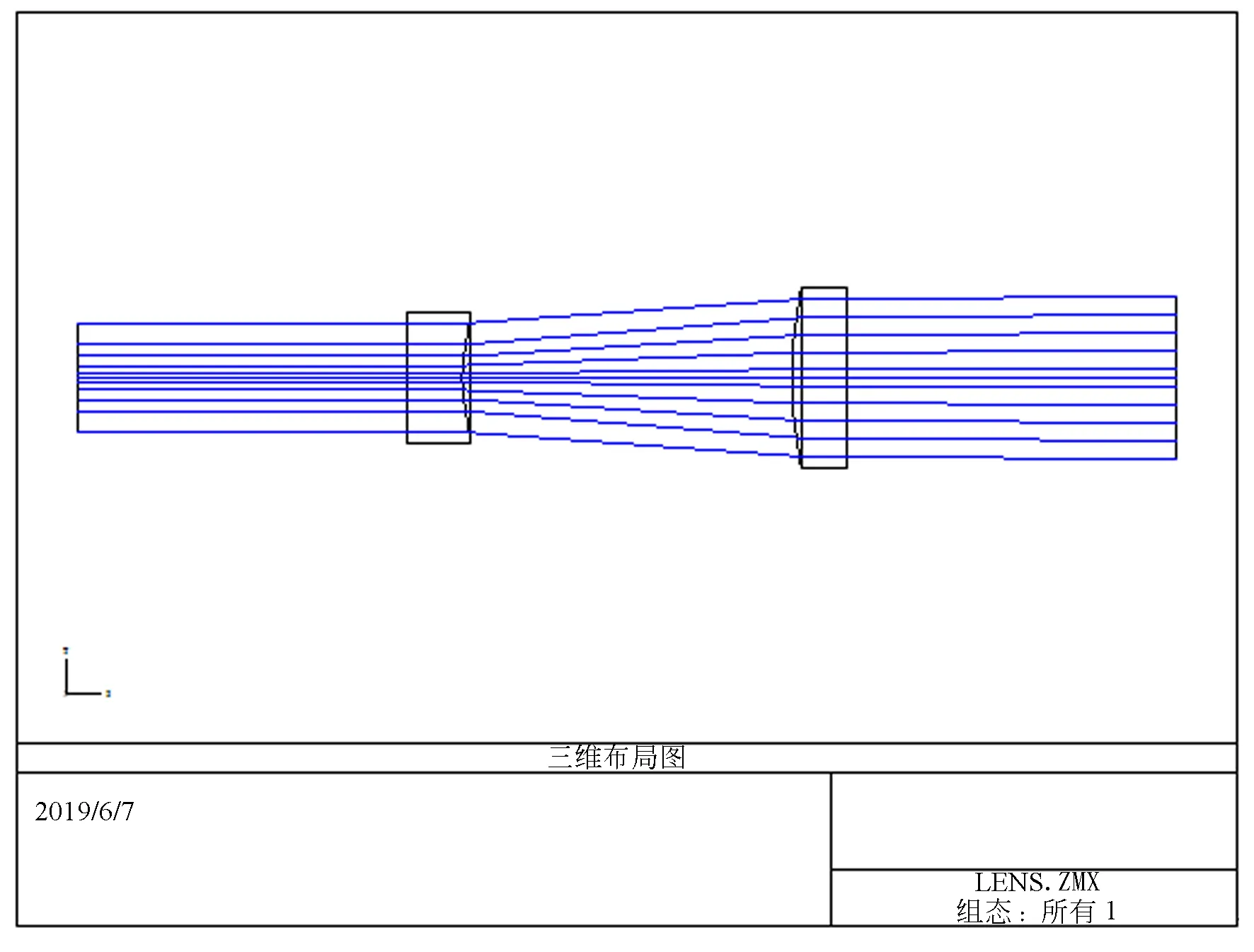
图2 非球面整形系统结构图Fig.2 Structure diagram of aspherical shaping system
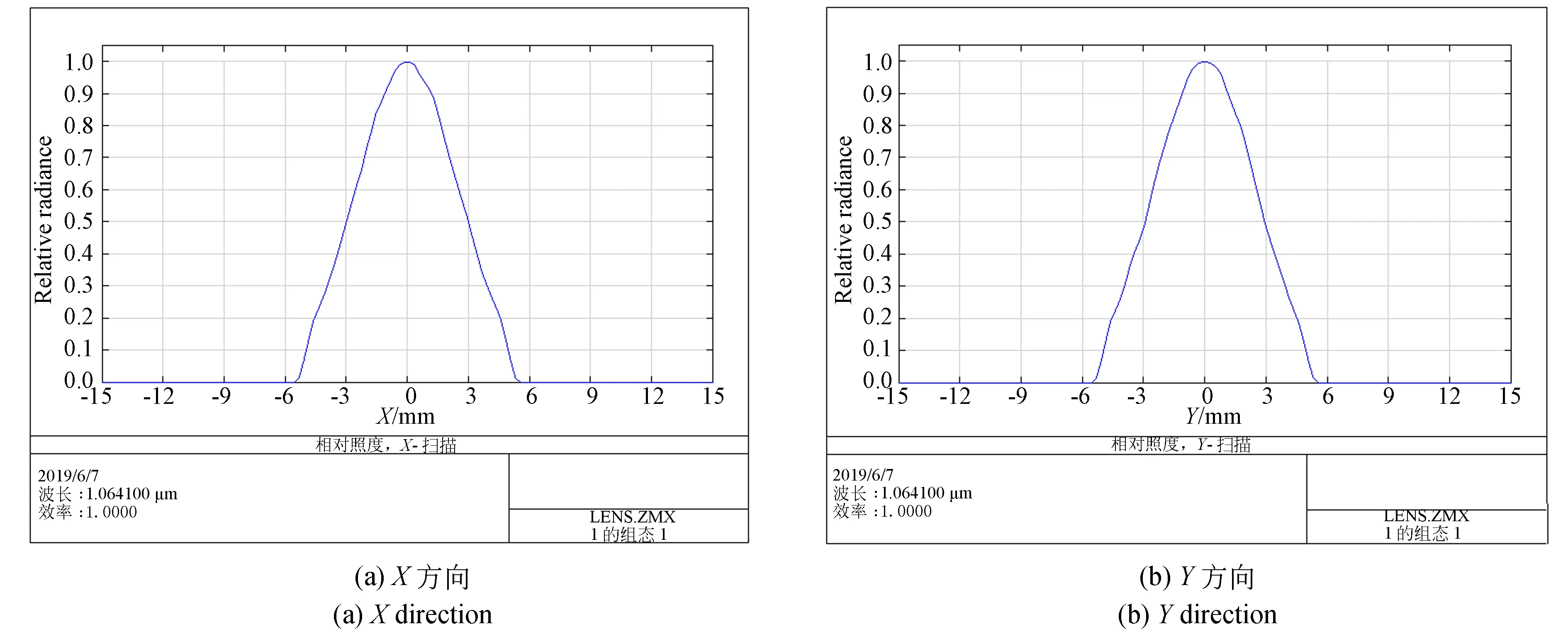
图3 不同方向入射光能量分布Fig.3 Energy distribution map of incidence light in different directions
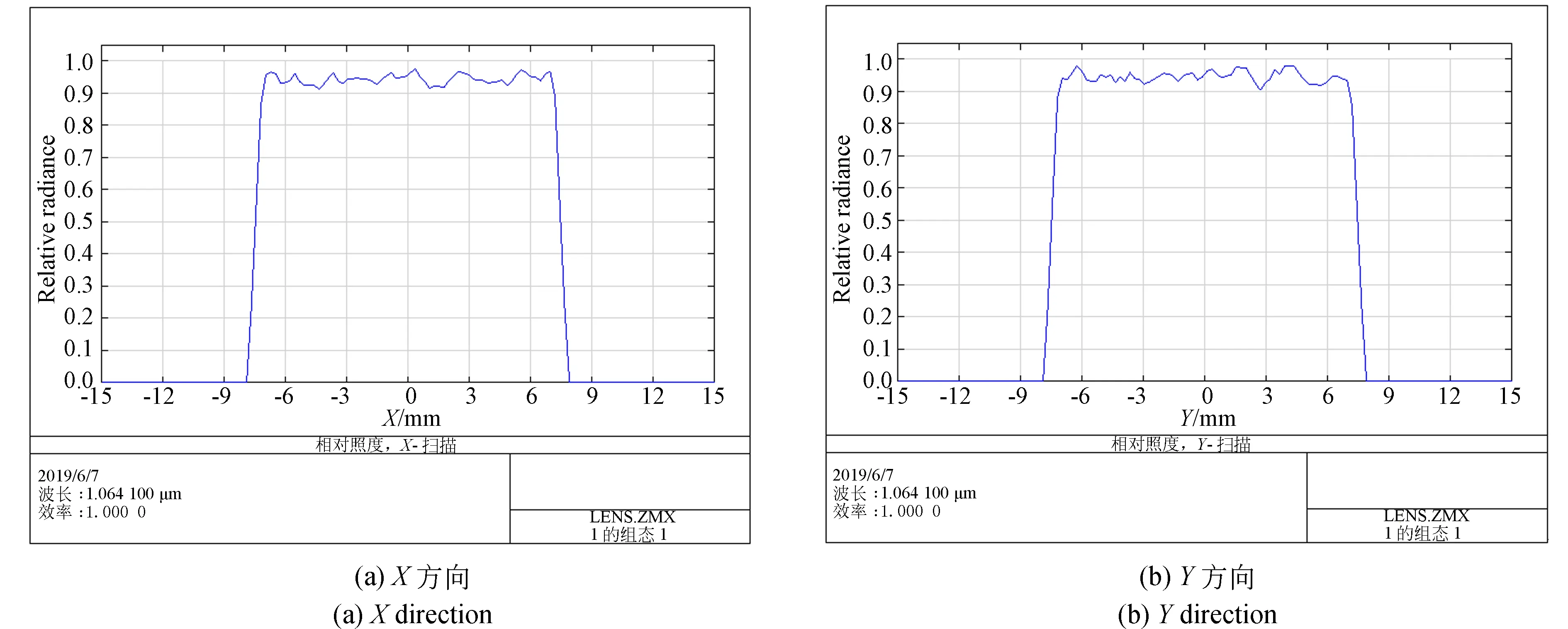
图4 出射光能量分布Fig.4 Energy distribution map of outgoing light in different directions
4.2 激光光斑形状整形系统及结果
一般来说,要使激光光束的输出光斑呈矩形,只需在系统后面添加两块相互垂直的柱透镜并进行默认优化后,调整到最为合适的曲率半径即可。在ZEMAX上设计后系统结构,具体参数见表3。
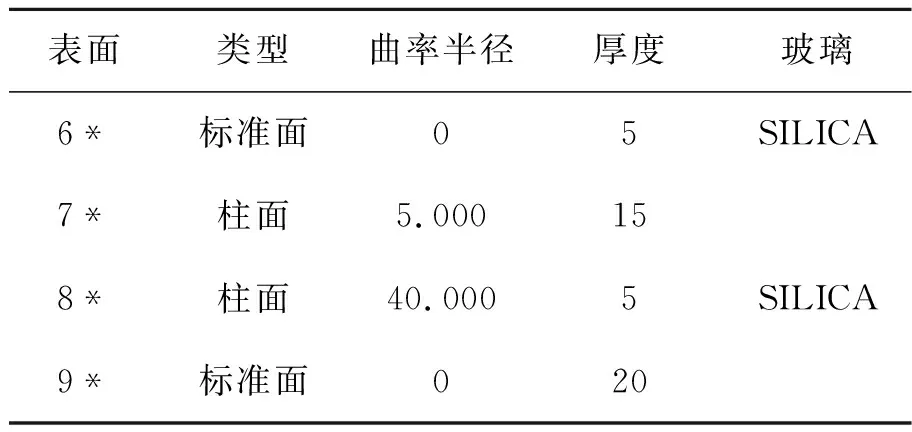
表3 光斑整形系统结构参数表Tab.3 Structural parameters of spot shaping system
光斑整形结果如图5所示,其中,图5(a)为入射光斑形状,图5(b)为出射光斑形状。由图5可以看到,激光束通过正交的柱透镜后出射光斑变为一个长10.68 mm,宽9.38 mm的光斑。
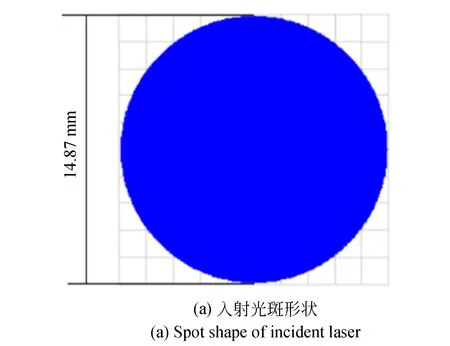
图5 激光束光斑图
4.3 整形系统在两个方向上的光束拉格朗日不变量
整形系统在X方向像方空间的NA为0.025 861 31,在Y方向像方空间的NA,对于输出激光光束质量可以采用拉格朗日不变量来表征。输出能量分布平顶的激光在XY方向上的拉格朗日不变量是相同的。系统在不同方向的光路如图6所示。输出能量分布平顶的激光在X,Y方向上的拉格朗日不变量是相近的,分别为6.715 92×10-4和6.728 24×10-4。由此可知两个方向的拉格朗日不变量基本相近。
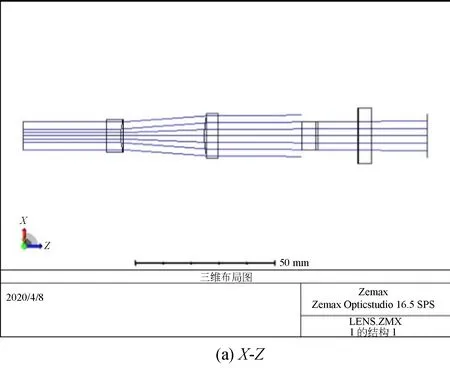
图6 X-Z和Y-Z方向光路
4.4 最终系统结构
通过对比整形后激光输出能量分布情况及激光光斑图,最终得到的整体系统如图7所示。
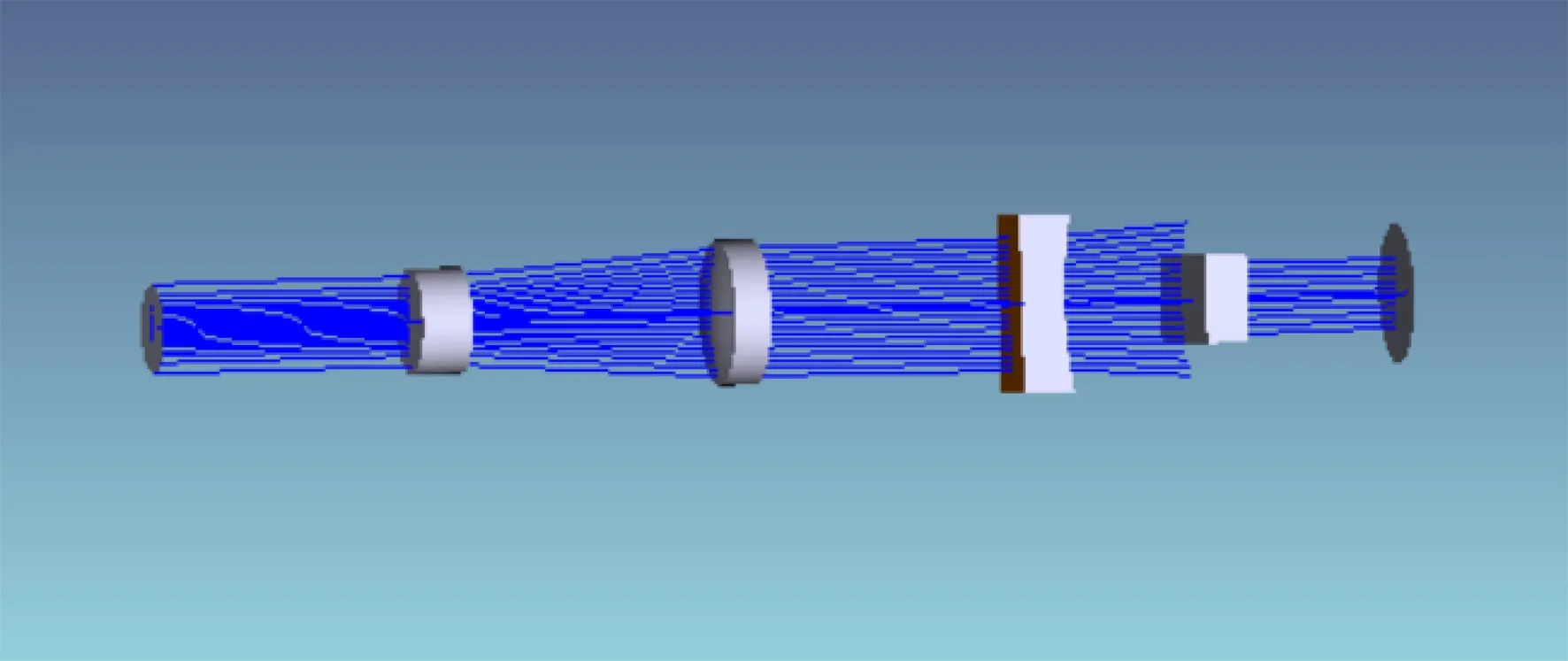
图7 激光系统结构模型Fig.7 Model of Laser system
在实际应用中,大功率激光器激光输出有工作焦深要求,而所谓的焦深指的是像面沿光轴移动一段距离后,激光输出能量分布无明显变化。为此本文比对了输出距离d分别为20,25,30 mm时输出平顶光的能量分布,如图8所示。其中,图8(a)为出射光X方向的能量分布,图8(b)为出射光Y方向的能量分布。
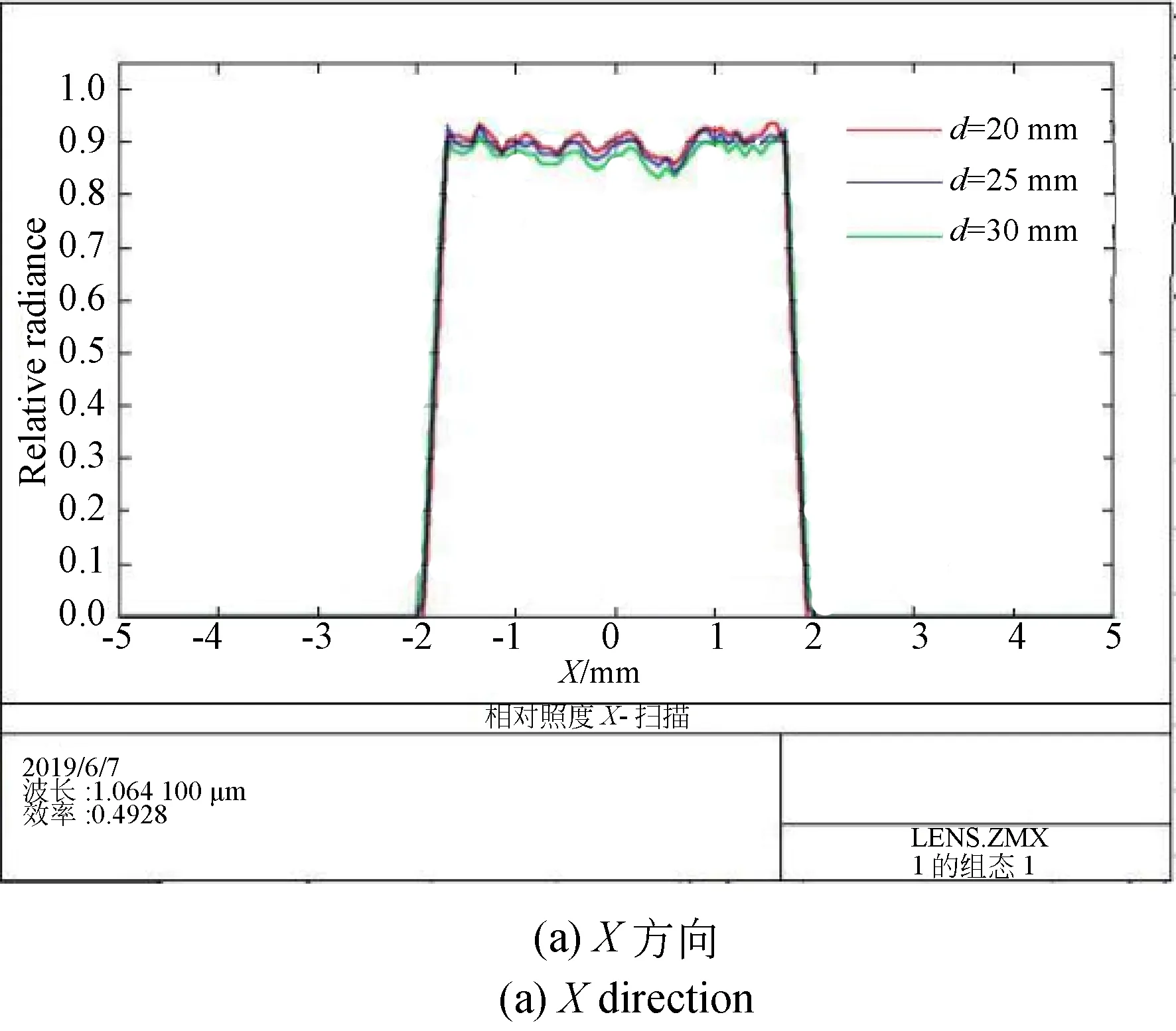
图8 不同方向出射光平顶光能量分布
假设光束能量分布的均匀度为γ,求其均匀度得到:
(8)
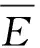
5 实验及结果
对设计的光学系统进行了激光均匀度测试。采用光束质量分析仪(型号:CinCam CMOS-12,分析软件:RayCi-Lite),辅助测试激光光束整形前后,激光束形及能量分布情况;准直后的高斯激光光斑束直径约为14.03 mm;整形后的平顶矩形光斑尺寸约为10.55×9.27 mm,光斑内激光能量密度分布均匀,光斑形状如图8所示。
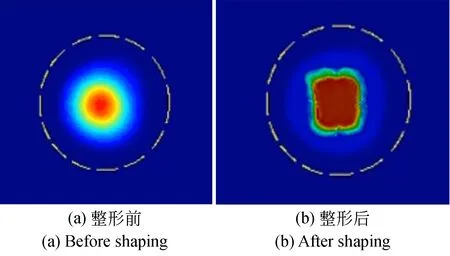
图9 激光光斑的能量分布Fig.9 Energy distribution of laser spot
利用本整形系统,在西安高斯激光科技有限公司自制的大功率激光清洗机上进行了实际产品激光清洗测试。采用的激光光源为武汉锐科光纤激光技术股份有限公司生产的500 W高功率脉冲光纤激光器(型号:RFL-P500)。针对实测激光清洗对象及要求(低碳钢板,尺寸为300 mm×100 mm,清洗效率>10 m2/h,基材允许的热影响深度<0.1 mm,基材硬度允许的变化范围<20 HV,表面清洁度要求:无肉眼可见红锈,粗糙度要求:不高于原粗糙度Ra值40%,金相组织要求:无明显组织转变;尺寸变形要求:无肉眼可见变形),设置的激光清洗参数为:40%激光器能量输出(单脉冲能量约为10 mJ),扫描速度为6 000 mm/s,脉冲宽度为160 ns,扫描频率为20 kHz,扫描延时100 μs,开光延时190 μs,关光延时100 μs,双S型扫描线形,聚焦后,手持清洗头平行于目标物移动。
使用金相显微镜(型号:Nikon EPIPHOJ300),对清洗及未清洗区的微观组织形貌进行观测,测试结果如图10所示。在未清洗区,表面组织大量铁锈;激光清洗完成后,铁锈被完全去除,仅留存基底材料,即铁素体和极少量的粒状珠光体;清洗未造成热影响,表面未出现明显损伤痕迹;使用轮廓仪(型号:TalySurf CCI 2000)在测试区域内任选3个点进行表面粗糙度测试,对应的表面粗糙度分别为:测试点①1.308 μm,测试点②1.303 μm,测试点③1.261 μm,材料表面粗糙度均匀,平均表面粗糙度为1.29 μm,说明整形后的激光光束能达到较好的清洗效果,满足实际使用要求。

图10 激光清洗效果
6 结 论
本文在对比常见高斯光束整形系统模型的基础上,结合大功率高斯激光光源的输出参数,采用伽利略式非球面透镜整形系统,避免了大功率激光束聚焦时对光学元件的损伤。采用平顶洛伦兹函数作为平顶光分布函数,计算了其映射函数;使用ZEMAX光学软件进行优化设计,系统工作焦深在20~30 mm时,平顶区激光能量均匀度均大于78.0%。经实际输出光斑能量测试,整形后光斑内能量分布均匀;实际的激光清洗测试证明设计的光学系统能够达到预期效果。进一步地,由于衍射效果,系统平顶光能量均匀度还有提升空间,后续还将对衍射效应进行优化;此外,为了获得能量均匀分布的矩形光斑,采用了尺寸小于光斑直径的柱透镜,造成部分能量损失,这也需要进一步优化。

