UPR-UPU-UR矢量推进机构的推进性能研究

杜晓强，于福杰，陈 原

(山东大学(威海)机电与信息工程学院，山东 威海 264209)

1 引 言

海洋占地表面积约71%，蕴藏着丰富的矿产资源和海洋生物资源，对海洋资源的勘测和开发是建设海洋强国、捍卫国家安全和实现海洋可持续发展的重要技术基础。装备各种探测仪器的水下机器人是探索海洋资源的重要设备，现有的绝大多数水下机器人具有路径规划简单、运动模式单一和推进效率低等缺点。因此，研制机动灵活的水下机器人对推动海洋资源探测技术的发展具有重要意义[1]。

机器人在执行水下作业任务的过程中，螺旋桨推进机构是保障水下机器人机动灵活作业的关键结构装置，单螺旋桨只能产生大小可变而方向固定(沿转动轴方向)的推进力。当水下机器人进行不同方向导向操纵运动时，比如俯仰和偏转，需要安装多个螺旋桨来产生多维方向推进力。但是，多个螺旋桨组合的推进方式会增加水下机器人的航行阻力，增大推进系统占据的空间，降低水下机器人低速航行时的水下定位能力。矢量推进技术作为一项新兴的推进技术，已经成熟地应用于航空飞行器上，它可以有效地提高航空飞行器的机动性和敏捷性，具有极其广阔的发展空间。然而目前国内外对水下机器人矢量推进技术的研究还较少。通过研究水下机器人矢量推进机构，实现单机构多姿态调整的矢量推进技术，对于提高复杂海洋环境下水下机器人的机动性和敏捷性具有重要的学术意义和工程应用价值。

目前，国内外对水下机器人矢量推进机构的研究还处于初级阶段，大部分矢量推进机构由传统串联机构或者并联机构组成。Lin等人[2-3]提出了具有喷水矢量推进技术的水下球形机器人，设计了由转动副组成的喷水矢量推进机构，通过矢量推进机构改变喷水推进力方向来调整机器人的姿态。高富东等人[4-5]设计了柔性传动轴构成的螺旋桨矢量推进装置，该柔性传动轴的偏摆和旋转会使螺旋桨推进装置实现矢量推进技术。方世鹏等人[6-8]设计了一种基于锥齿轮调向的矢量推进机构，该机构由一个电机给螺旋桨提供动力，另外两个电机改变锥齿轮的位置角度以调整螺旋桨的空间姿态。郑昆山等人[9-10]基于蜗轮蜗杆结构设计了喷水矢量推进装置，矢量推进装置中的翼管与空心轴固联，高压水流由蜗轮带动的翼管转动实现推进力的矢量化。基于并联机构的矢量推进机构除了能提供前进推进力外，还可根据水下机器人的导向操纵任务需求，改变螺旋桨推进姿态来调整推进力方向，产生其它多维方向上的推进力，使得水下机器人在低速航行时的导向操纵运动不依赖于航行速度，极大地提高了其低速航行时的水下定位能力[11-13]。Roque等人[14]设计了基于Stewart六自由度并联机构的矢量推进水下机器人，它的螺旋桨安装于并联机构动平台上，螺旋桨的姿态会随动平台姿态变化而变化。Saltaren等人[15]借助Stewart-Gough并联机构研制了REMO I型遥控水下机器人，使用了连接头部引导环与尾部随动环的六个直线驱动电机，实现螺旋桨的矢量推技术。目前对矢量推进机构的研究仅局限于传统串联机构或Stewart六自由度并联机构。然而，传统串联机构的自重负荷比大，很难适应深海重压环境，虽然六自由度并联机构在灵活性和自重负荷比等方面满足导向操纵动作要求，但是其工作空间小、结构和控制较复杂，对水下机器人运动的灵活性和敏捷性影响较大，也很难应用于工程实际。少自由度并联机构的设计制造更为简单，导向操纵动作也不需要空间所有的自由度，因此基于少自由度并联机构的矢量推进机构将为矢量推进方式提供新的设计理念。

为了实现水下机器人的推进装置具备空间姿态调整和大转矩的动力传递功能，本文提出了UPR-UPU-UR矢量推进机构。首先，运用螺旋理论计算了矢量推进机构的自由度，基于解析法构建了矢量推进机构的位置模型。其次，推导出了矢量推进机构的输出矢量和输入矢量之间的关系，并采用粒子群优化算法对矢量推进机构进行了位置正解计算。然后，基于矩阵分析法从速度雅克比矩阵和机构特征性角度研究了机构奇异性，计算了矢量推进机构动平台的工作空间。最后，搭建了UPR-UPU-UR矢量推进机构的实验平台，并进行了试验研究。

2 UPR-UPU-UR矢量推进机构的创新设计

2.1 设计思想与坐标系构建

水下机器人矢量推进机构是通过改变螺旋桨推进姿态来改变推进力的方向，它的不同运动方案直接关系到矢量推进技术实现原理。任何导向操纵动作都可以分解为螺旋桨旋转和螺旋桨空间姿态调整这两个运动，它们两者之间可为解耦运动关系，也可为耦合运动关系，不同运动关系将对应着不同矢量推进机构运动方案。如果为解耦运动关系，仅需要矢量推进机构提供姿态调整功能。当它们两者之间为耦合运动关系时，除了矢量推进机构完成的螺旋桨空间姿态调整功能外，还需要再增加一条传动链，将驱动源的旋转运动传递给螺旋桨。本文基于矢量推进机构上的螺旋桨旋转运动及其空间姿态调整运动之间的耦合运动关系，创新设计了UPR-UPU-UR矢量推进机构，不仅能为水下机器人提供推进力，而且可准确灵活地调整螺旋桨的姿态，实现水下机器人的姿态调整功能。

如图1所示是本文提出的UPR-UPU-UR矢量推进机构，该矢量推进机构的动平台与静平台通过三条运动支链连接。由一个U副、一个移动副P和一个转动副R组成支链，称为UPR支链。由一个移动副P和两个U副连接组成支链，称为UPU支链。由一个U副和一个转动副R组成支链，称为主轴支链UR。这三条运动支链都是通过静平台上的交流伺服电机进行驱动，一个电机驱动主轴支链的螺旋桨为水下机器人提供推进的动力，另外两个电机驱动两条支链的丝杠转动，通过改变支链的P副运动引起机构动平台的姿态改变，以此灵活地调整矢量推进机构姿态以改变水下机器人的运动方向。

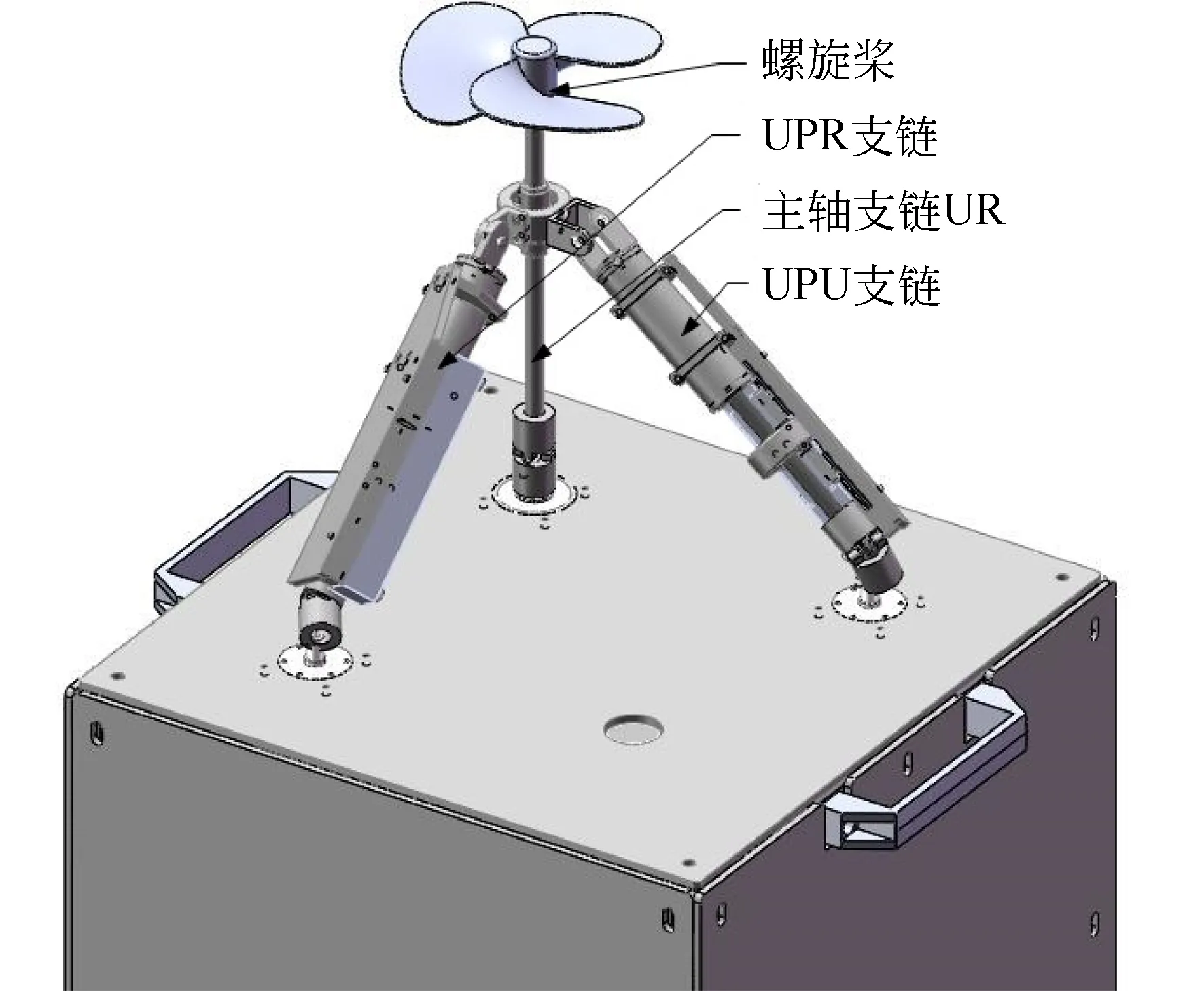
图1 UPR-UPU-UR矢量推进机构的三维图Fig.1 Three dimension of UPR-UPU-UR vector propulsion mechanism

如图2所示，在静平台和动平台上分别建立静坐标系和动坐标系，记为O-XYZ和o-xyz。在主轴支链UR下端的U副中心标记为点O，在UPR支链下端的U副中心标记为点D1，在UPU支链下端的U副中心标记为点D2。在主轴支链UR上端的R副中心标记为点o，在UPR支链上端的R副中心标记为点d1，在UPU支链上端的U副中心标记为点d2。主轴支链UR中R副垂直于动平台，X轴正方向是由点O指向点D1的方向，Y轴正方向是由点O指向点D2的方向，Z轴方向由右手螺旋定则确定。x轴正方向是由点o指向点d1的方向，y轴正方向是由点o指向点d2的方向，z轴方向由右手螺旋定则确定。设定OD1和OD2的长度均为A=270 mm，od1和od2的长度均为a=47 mm，Oo的距离为e=220 mm。

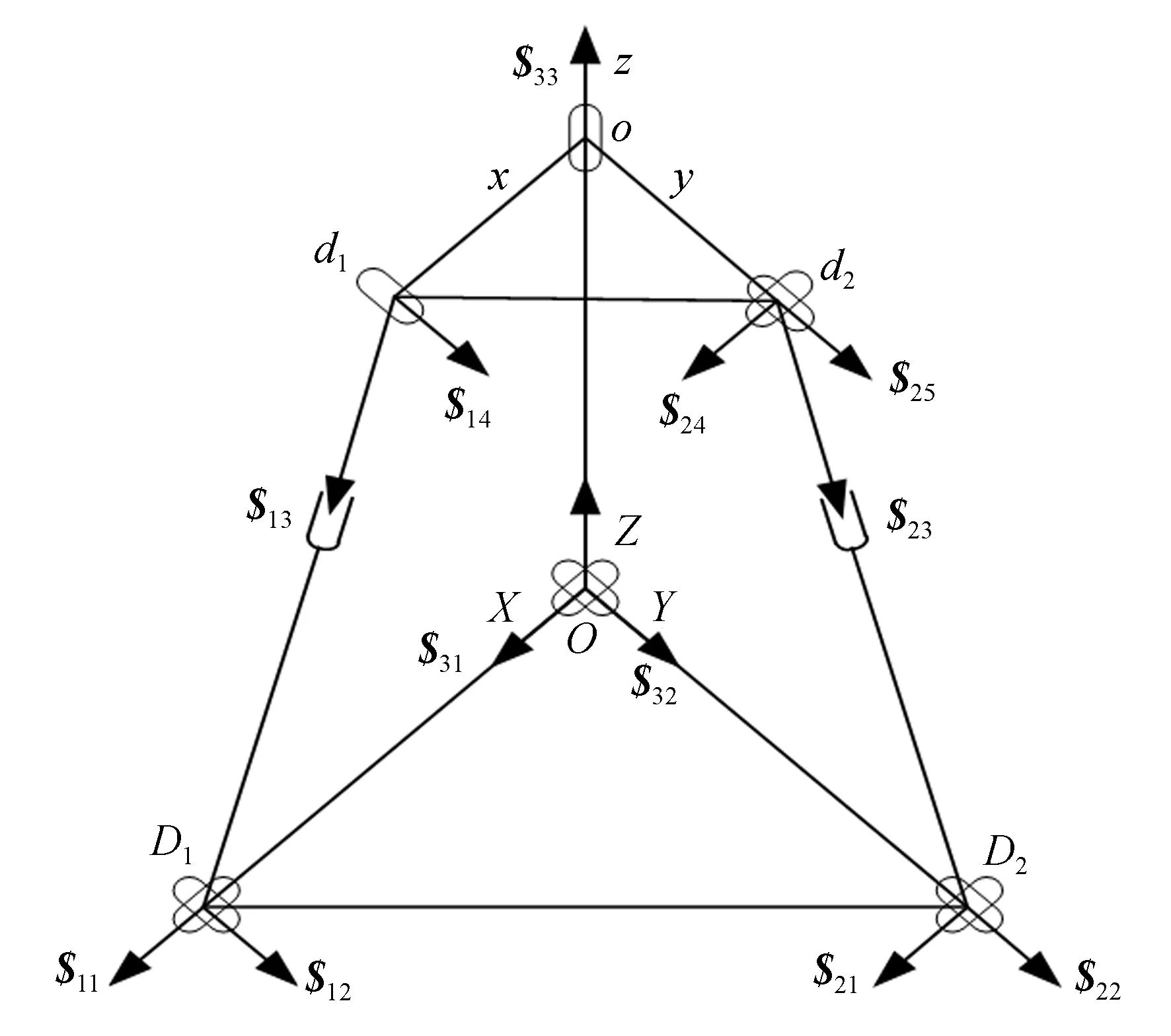
图2 UPR-UPU-UR矢量推进机构的螺旋分布图Fig.2 Screw distribution diagram of UPR-UPU-UR vector propulsion mechanism

2.2 UPR-UPU-UR矢量推进机构的自由度计算

当机构的动坐标系的z轴与静坐标系的Z轴重合时，动坐标系的x轴和y轴分别与静坐标系的X轴和Y轴平行时，将动平台的位置设置为矢量推进机构的初始位置。用$ij表示机构中运动副的方向向量，用rij表示机构中运动副的中心点坐标(i=1, 2, 3;j=1, 2, 3, 4, 5)。

在初始位置下，点d1在静坐标系下的位置为r14=(a,0,e)，点D1在静坐标系下的位置为r12=(A, 0, 0)，那么UPR支链的运动螺旋可以表达为：

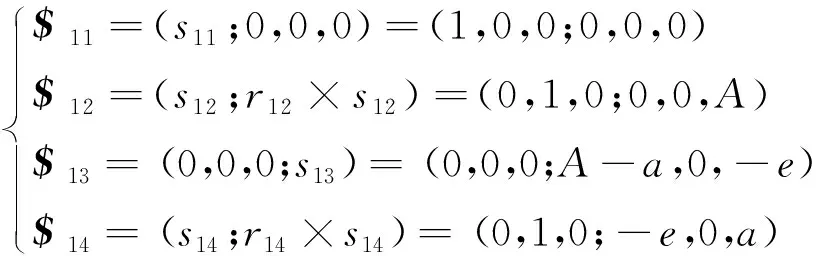
(1)

进一步，可以得到其约束螺旋为:

(2)

在初始位置下，点d2在静坐标系下的位置为r24=r25=(0,a,e)，点D2在静坐标系下的位置为r21=(0,A, 0)，那么UPU支链的运动螺旋可以表达为：

(3)

进一步可以得到其约束螺旋为:

(4)

在初始位置下，点o在静坐标系下的位置为r33=(0, 0,e)，主轴支链UR的运动螺旋可以表达为：

(5)

进一步，可以得到其约束螺旋为:

(6)

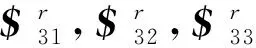
那么，机构动平台的约束螺旋可以表达为:

(7)

接下来，可以求解得到如下机构动平台约束螺旋的反螺旋：

(8)

根据式(8)，可知UPR-UPU-UR矢量推进机构具有两个转动自由度。机构有6个约束螺旋，实际上构成4系螺旋，所以冗余约束数ν=2。由UPR- UPU-UR矢量推进机构的结构可知，机构所有的构件数n=7，运动副总数g=8，运动副的相对自由度fi累积求和为12，局部自由度ζ=0。公共约束λ=0，所以机构的阶数d=6。将上述各参数代入Kutzbach-Grübler公式[16]，可以得出UPR-UPU-UR矢量推进机构的自由度为：

(9)

3 UPR-UPU-UR矢量推进机构的运动学建模

3.1 UPR-UPU-UR矢量推进机构的位置反解模型

位置正反解模型是分析机器人矢量推进机构运动性能的基础[17-19]。为方便表达，规定sinθ=sθ，cosθ=cθ，tanθ=tθ。在初始位置下，动平台通过绕静坐标系O-XYZ的X轴旋转β角后，继续绕新生成的静坐标系O-XYZ的Y轴旋转α角实现姿态的变化。则矢量推进机构的从静坐标系O-XYZ运动到动坐标系o-xyz的旋转变换矩阵可表达为：

(10)

初始状态下，动平台上的点d1在动坐标系o-xyz下位置为od1=(a, 0, 0)，点d2在动坐标系o-xyz下位置为od2=(0, a, 0)，动坐标系的原点o的在静坐标系O-XYZ下位置为Oo=(0, 0,e)。

经过旋转变换矩阵转换后，点d1、点d2、点o在静坐标系下O-XYZ的位置变为：

(13)

由静坐标系O-XYZ的点D1的位置为OD1=(A, 0, 0)，点D2的位置为OD2=(0,A, 0)，得到如下闭环矢量关系：

D1Od1=OOo+OoOd1-OD1，

D2Od2=OOo+OoOd2-OD2，

(14)

主轴支链UR的长度为固定值，剩余两条支链的长度是变化的，且UPR支链和UPU支链的矢量分别为：

(15)

矢量推进机构中U副的转动范围有限，且L1，L2和L3均是正值。主轴支链UR与动平台固接，取点o为动平台的参考点，那么可以推导出UPR支链的长度L1和UPU支链的长度L2分别为：

L1=|D1Od1|=

L2=|D2Od2|=

(16)

由式(16)可见，α和β决定着机构动平台的位姿。当α和β确定后，动平台参考点o在静坐标系O-XYZ下的位置Oo=(Oox,Ooy,Ooz)也便确定了。

如果动平台的姿态角按照一定规律发生变化，那么可以通过反解模型求出两条支链的长度变化规律。假设对动平台的姿态角随时间t的变化表达式为：α=15sin(πt/2)和β=15sin(πt/2)，且t的取值范围为[0, 12]。根据该矢量推进机构的位置反解公式(16)，在MATLAB中可以求解两条支链的长度L1和L2关于时间的变化曲线如图3所示。

图3 两条支链的长度随时间的变化曲线Fig.3 Variation curve of the length of branch chains

从图3可以看出，矢量推进机构的支链UPR与支链UPU的长度变化曲线呈现近似于正余弦函数图像，变化曲线的增减趋势恰好相反。矢量推进机构的两条支链的长度变化曲线较为平滑，不存在阶跃突变现象，说明矢量推进机构的结构设计和参数选择较为合理，表明其位置反解模型的正确性。

3.2 UPR-UPU-UR矢量推进机构的位置正解模型

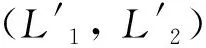
应用PSO算法进行矢量推进机构的位置正解建模，具体建模过程如下:

(1)构建粒子适应度函数‖C‖F作为优化目标函数，设定当粒子适应度函数值小于10-4时结束算法。

(17)

(2)初始化PSO算法的参数

为提高计算效率，根据动平台姿态运动范围[21]设置搜索范围，并设置如表1所示的种群规模、学习因子、最大迭代次数、最大搜索速度和标准惯性权重等基本参数。

表1 粒子群优化算法参数

(3)优化目标函数的三维空间仿真

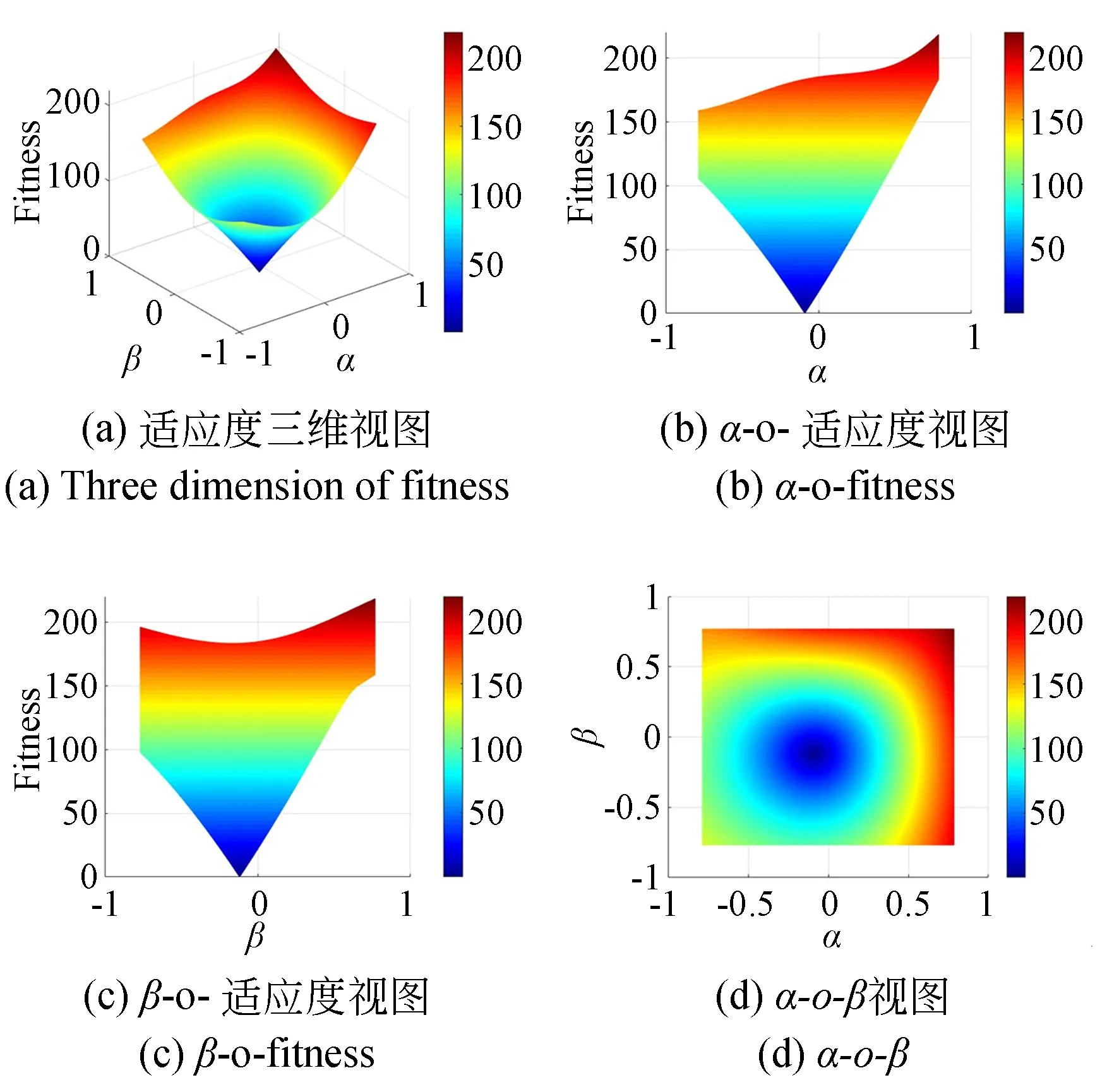
图4 算例一(L1=330 mm，L2=335 mm)Fig.4 The first example(L1=330 mm，L2=335 mm)

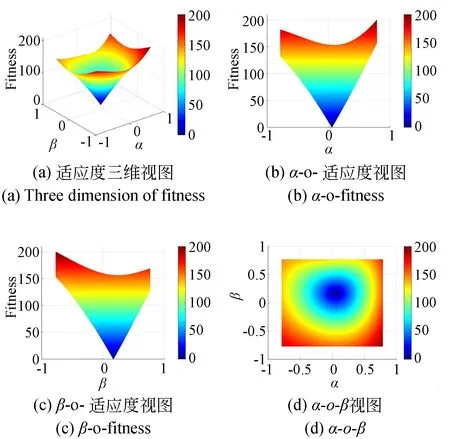
图6 算例三(L1=303 mm，L2=280 mm)Fig.6 The third example(L1=303 mm，L2=280 mm)

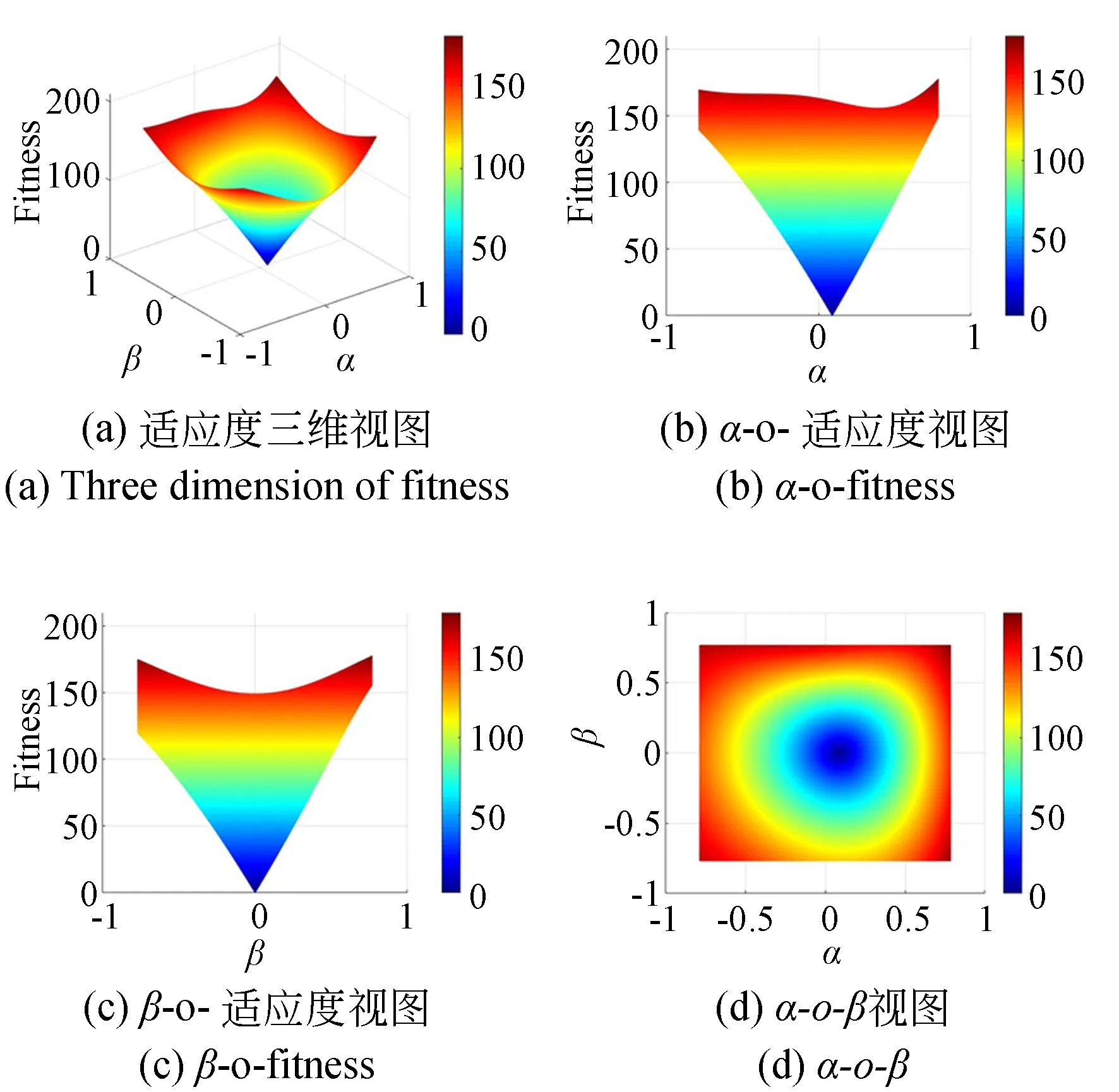
图7 算例四(L1=296 mm，L2=313 mm)Fig.7 The fourth example(L1=296 mm，L2=313 mm)

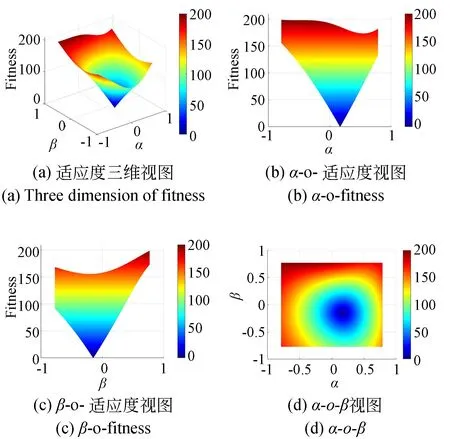
图8 算例五(L1=280 mm，L2=340 mm)Fig.8 The fifth example(L1=280 mm，L2=340 mm)

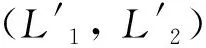
(4)粒子速度及位置更新过程

首先将每一个粒子的初始位置都设置为自身最佳位置Pid，同时计算并比较各粒子的适应度函数。寻找到粒子群中最佳的粒子作为全局最优粒子Pgd，随后更新粒子的速度和位置，其更新公式为：

(18)

(19)

通常在个体的各维度上设置搜索区间边界，防止个体微粒在某一个维度上超出搜索范围。设置新的粒子速度和位置进行适应度计算，将每一次的计算结果与上一次结果进行比较。如果使用当前位置来计算的适应度结果优于自身之前的最佳位置的适应度结果，那么用该粒子当前位置替代之前位置Pid。同理，若种群中的最佳粒子优于Pgd，则替代之。循环迭代过程，直至当适应度函数值小于或等于10-4后停止迭代，即得到输入支链长度值对应的动平台姿态角(α,β)。经过上述算例分析，结果如表2所示。各算例PSO算法的粒子适应度函数值随着算法迭代次数增加的变化关系如图9所示。

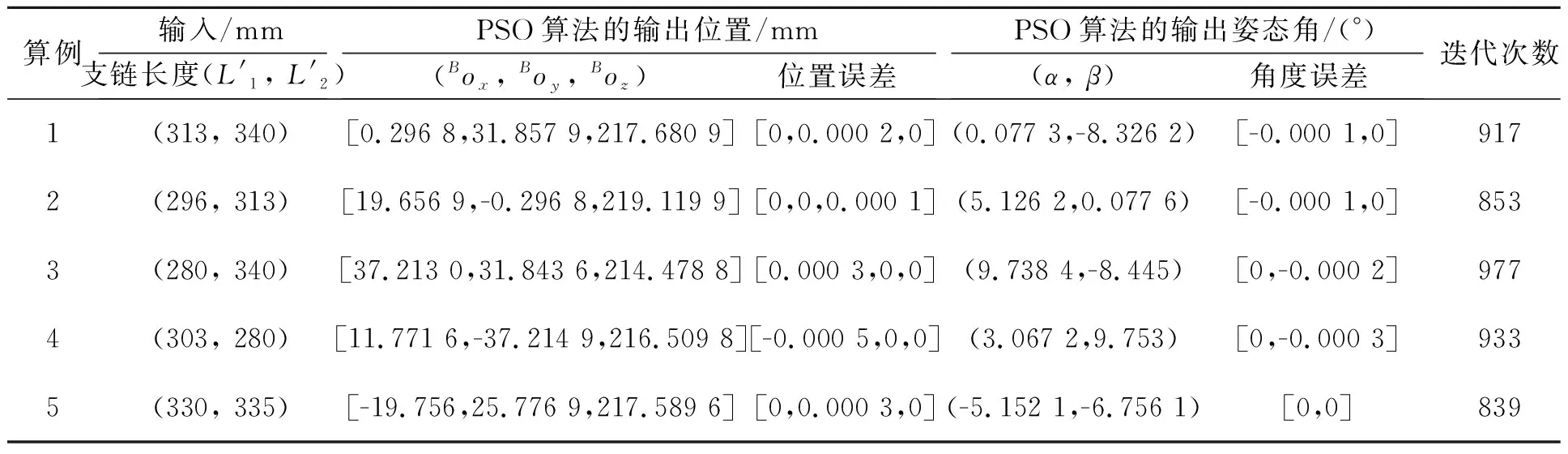
表2 位姿正解算例结果

图9 各算例PSO算法适应度曲线Fig.9 PSO algorithm fitness curves of different examples

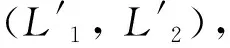
3.3 UPR-UPU-UR矢量推进机构的速度建模

本小节基于位置模型求解机构的速度雅克比矩阵，对UPR-UPU-UR矢量推进机构进行速度建模[23]。对公式(16)两边分别对时间t求偏导数，可得：

(20)

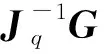
据此得到该矢量推进机构的动平台和静平台之间的速度关系表达式：

(21)

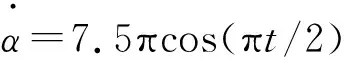
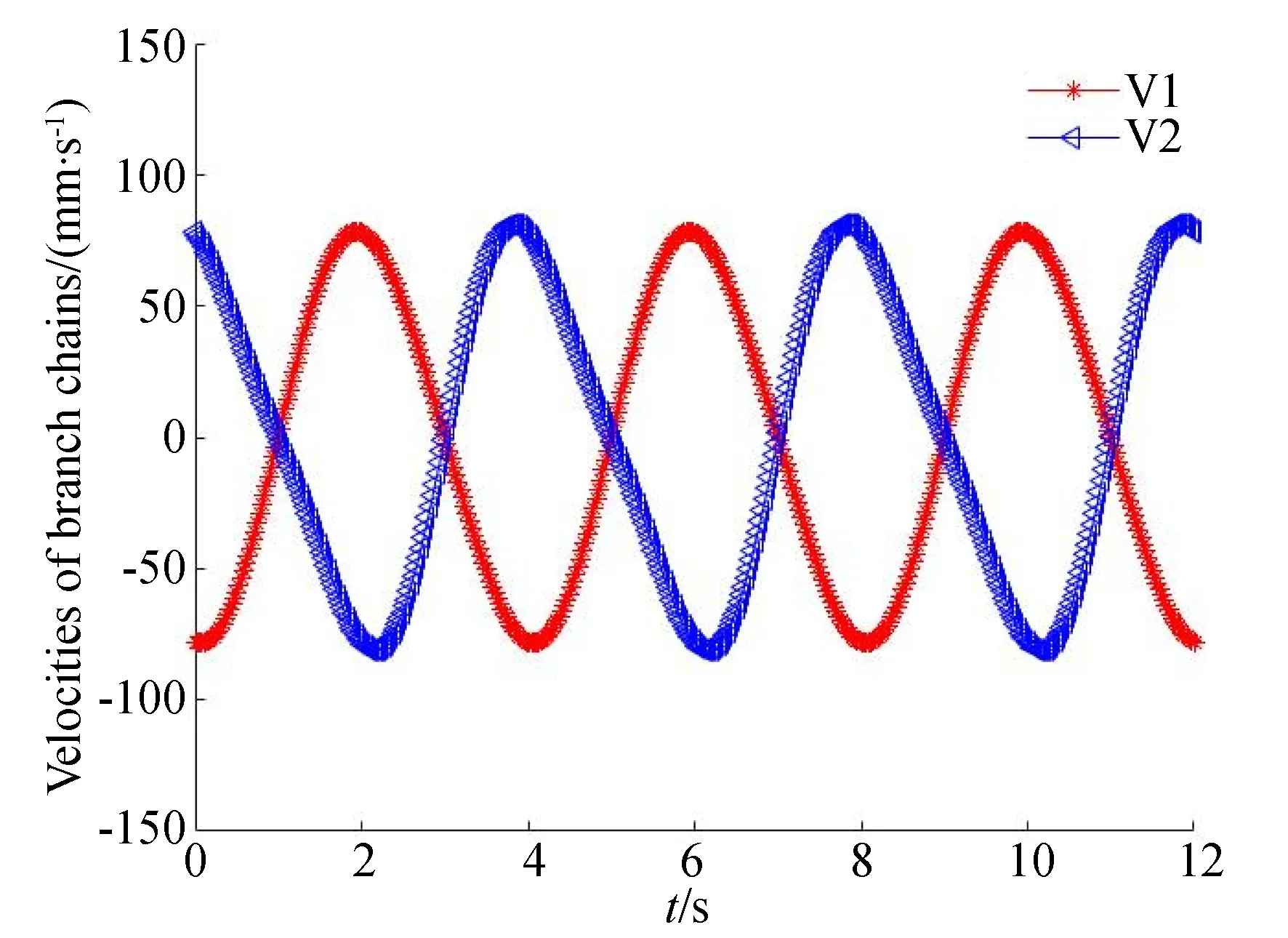
图10 两条支链的速度随时间的变化曲线Fig.10 Variation curve of velocity of branch chains

从图10可以看出，矢量推进机构的支链UPR和支链UPU的速度随时间变化呈现近似正余弦函数变化规律，两条支链的速度始终在一定范围内进行波动，两条变化曲线比较平滑，没有发生阶跃突变的现象。同时对比分析图3所显示的支链长度随时间的变化曲线，可见支链的速度变化规律符合支链长度的变化规律。两图证实了矢量推进机构的位置建模的正确性与合理性。

3.4 UPR-UPU-UR矢量推进机构的奇异性分析

当并联机构动平台运动处于奇异位形时，其实际自由度发生变化，影响机构的运动性能，同时改变机构的静力学性能、刚度、稳定性及灵巧度[24]。根据机构奇异位形的特点将机构奇异性分为边界奇异和内部奇异[25]。本文采用雅克比矩阵分析法对该矢量推进机构进行奇异性分析。

机构中各支链的长度L1，L2和L3均是正值，不可能存在|Jq|=0的情况，矢量推进机构不会增加自由度，导致机构运动失去控制，故不存在反解奇异。机构各支链长度是大于零的正数，即|Jq|≠0，不存在|Jq|和|G|同时为零，因此矢量推进机构不可能存在混合奇异。机构各支链长度均大于零的正数，因此|Jq|≠0。根据式(20)中的|G|=0时，G11G22-G12G21=G11G22=0。所以矢量推进机构的正解奇异具有以下两种情况：

(1)当G11=A(asα-ecα)=0时，α=arctan(e/a)，代入相关尺寸，解得α=77.94°，这种奇异位形称为第一类正解奇异。此时机构中UPR支链的丝杠长度不足，其位形如图11(a)所示的第一类奇异。

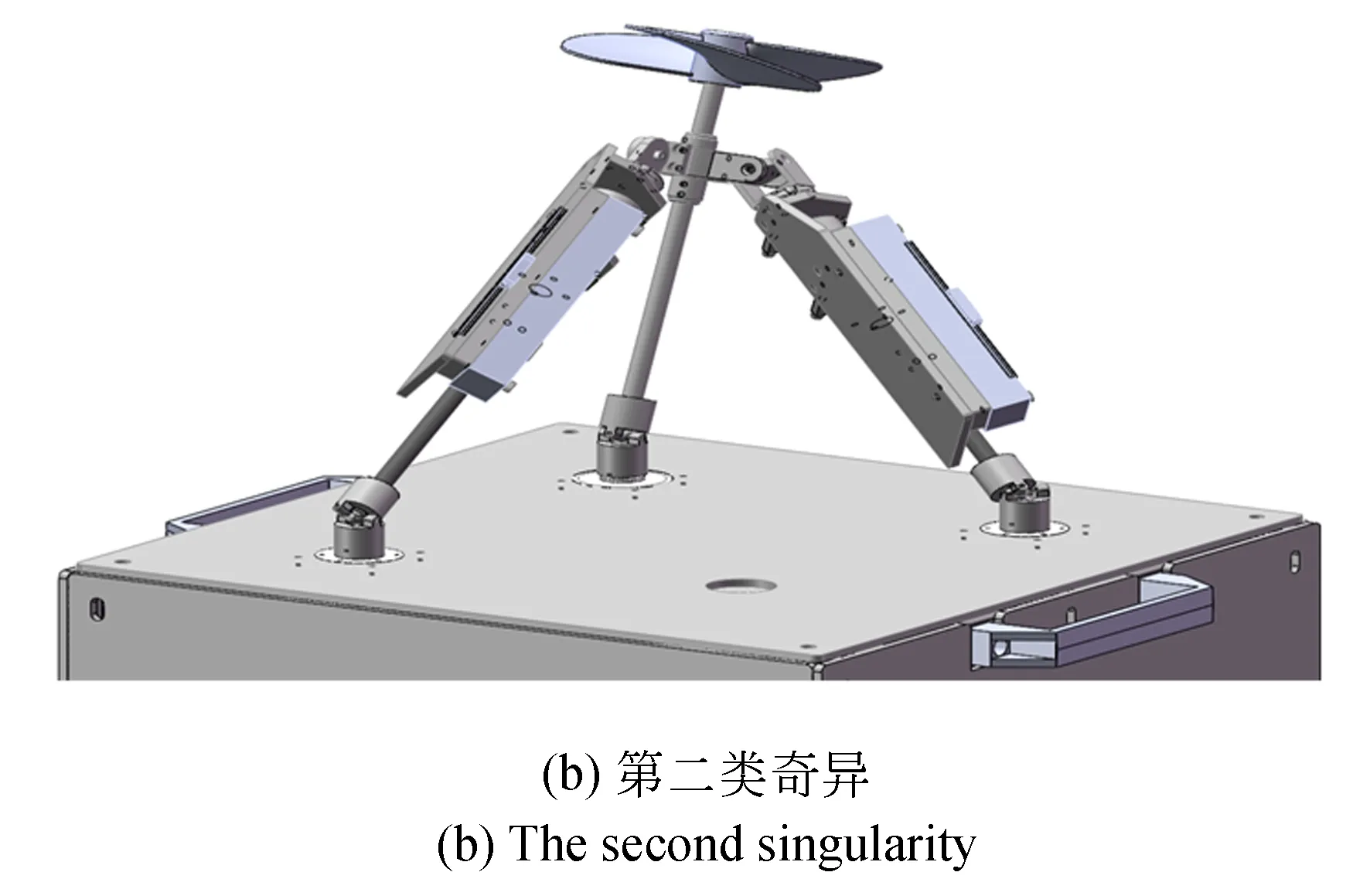
图11 UPR-UPU-UR矢量推进机构正解奇异Fig.11 Positive solution singularity for UPR-UPU-UR vector propulsion mechanism

(2)当G22=A(asβ-ecαcβ)=0，所以β=arctan(ecosα/a)，假设α处于转动角度的最大值，代入相关尺寸，解得β=44.36°。这种奇异位形称为第二类正解奇异。此时该机构中UPU支链的丝杠长度不足，其位形如图11(b)所示的第二类奇异。

3.5 UPR-UPU-UR矢量推进机构的工作空间分析

机构的工作空间是衡量矢量推进机构推进性能的重要指标。影响工作空间的因素主要有机构本身结构、支链长度限制、运动副转角限制、支链间的互相干渉限制和奇异位形限制等。本文将通过数值搜索法求解矢量推进机构的工作空间。

(1)支链长度限制

UPR-UPU-UR矢量推进机构的两条支链的丝杠转动长度是有限的，故两条支链的长度L1和L2存在最小值和最大值表示成Li min和Li max，则变化范围可以表示成Li min≤Li≤Li max(i=1, 2)。设定Li min=264 mm，Li max=364 mm。设定OD1和OD2的长度均为A=270 mm，od1和od2的长度均为a=47 mm，Oo的长度为e=220 mm。

(2)运动副转角限制

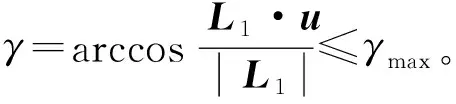
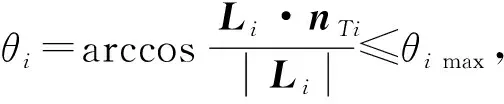
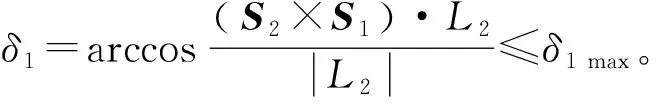
(3)支链间的相互干涉限制和奇异位形限制

分析并联机构的工作空间时，需要考虑机构的实际尺寸，各支链间有可能发生互相干涉。UPR-UPU-UR矢量推进机构有两个自由度，各支链间发生运动干涉的概率较小，所以求解此机构工作空间不需要考虑各支链之间的相互干涉限制。当UPR-UPU-UR矢量推进机构处于奇异位形时，影响其矢量推进性能，所以求解此机构工作空间需要避免机构的正解奇异位形。

综上所述，矢量推进机构工作空间的限制表达式如式(22)所示：

(22)

将矢量推进机构的动平台原点o相对于静坐标系的位置(esα, -ecαsβ,ecαcβ)T作为工作空间的参考点，经MATLAB计算并绘制三维图，得到如图12所示的UPR-UPU-UR矢量推进机构动平台的工作空间。动平台运动的工作空间的形状为球面的一部分，图12(a)表示其在O-XYZ三维视图，图12(b)表示其在XOZ平面投影视图，图12(c)表示其在YOZ平面投影视图，图12(d)表示其在XOY平面投影视图，图中可见，工作空间的形状关于X轴对称且关于Y轴对称。

图12 UPR-UPU-UR矢量推进机构动平台工作空间Fig.12 Workspace of moving platform for UPR-UPU-UR vector propulsion mechanism

在UPR-UPU-UR矢量推进机构中，在初始位置下，绕X轴旋转β角，后绕Y轴旋转α角。当β的角度取值范围是[-45°，45°]，α的角度取5°，矢量推进机构动平台的运动轨迹如图13所示。动平台上点o的运动轨迹是一条形似为抛物线的曲线，图13(a)表示其在O-XYZ三维视图，图13(b)表示其在XOZ平面投影视图，图13(c)表示其在YOZ平面投影视图，图13(d)表示其在XOY平面投影视图，图中可见，该运动轨迹是关于X轴对称。

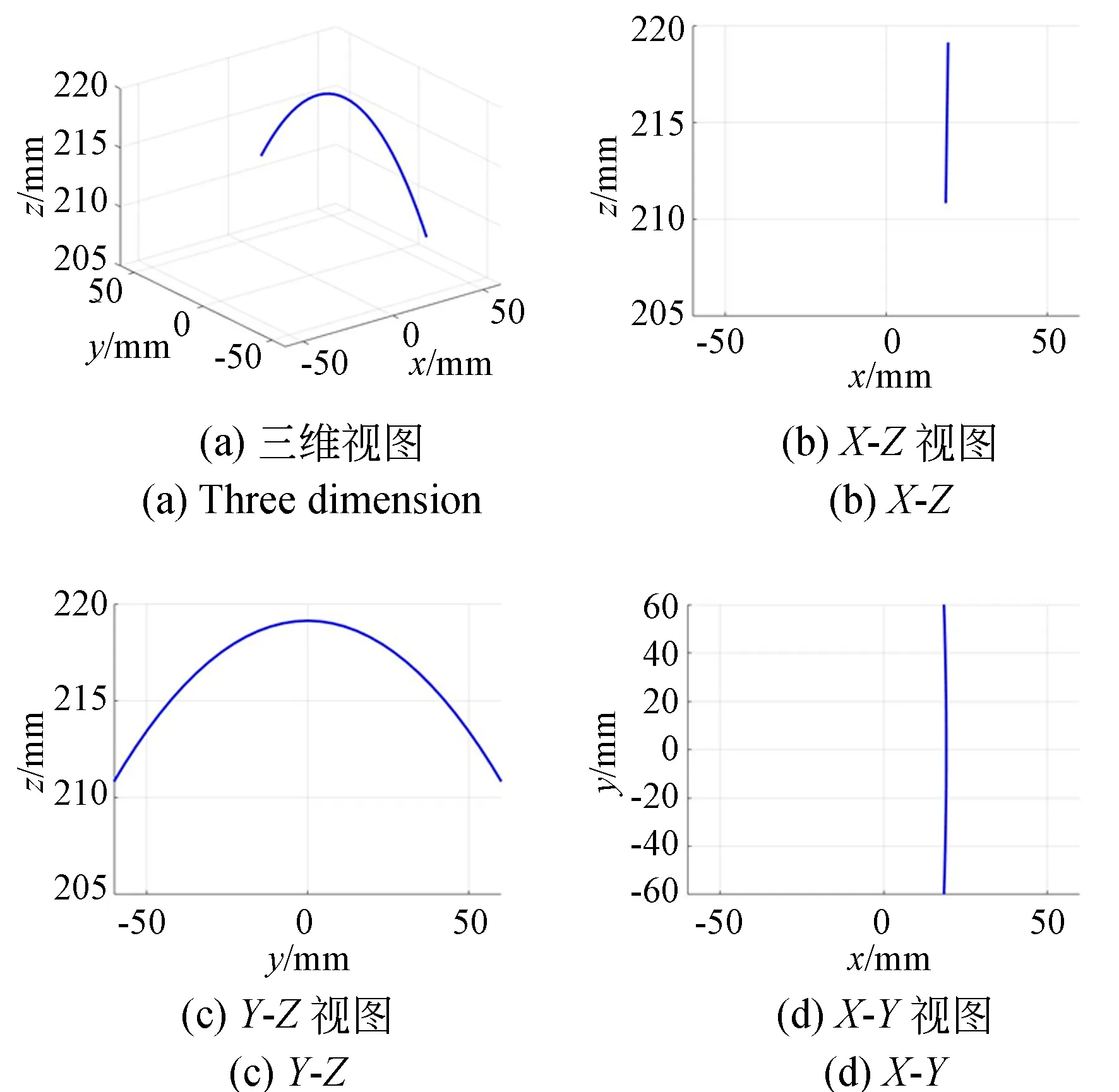
图13 UPR-UPU-UR矢量推进机构动平台运动轨迹Fig.13 Trajectory of moving platform for UPR-UPU-UR vector propulsion mechanism

4 实验验证

为了进一步验证矢量推进机构的矢量推进性能，搭建了如图14(a)所示的UPR-UPU-UR矢量推进机构实验平台。实验平台主要由UPR-UPU-UR矢量推进机构、交流伺服电机驱动模块、传感模块和控制模块组成。传感模块由光栅尺、数显表和航姿传感器组成，其中：光栅尺测量两条支链的长度变化，分别传输至数显表和计算机的串口助手，实时准确读取矢量推进机构的两条支链长度变化数据。利用航姿传感器测量矢量推进机构的动平台的俯角、仰角和转角的变化，并向计算机反馈动平台的位姿变化。如图14(b)所示为UPR-UPU-UR矢量推进机构实验平台的控制原理图。图14(c)所示为实验平台的人机交互界面，通过设置机械部分的运行参数和输入运行程序代码可以控制该矢量推进机构的运行情况，可以实时调整机构动平台的姿态。

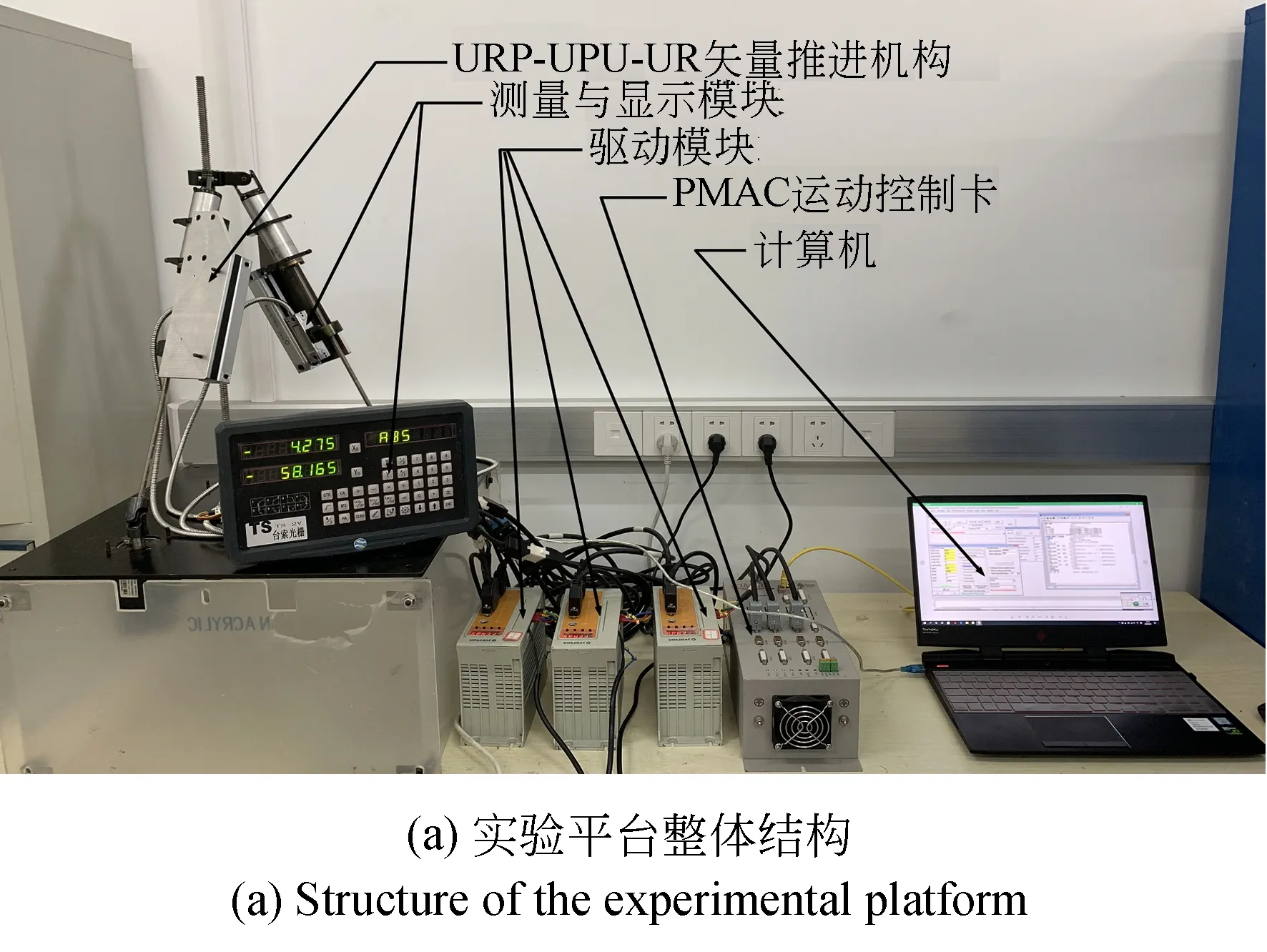
图14 UPR-UPU-UR实验平台Fig.14 Experimental platform for UPR-UPU-UR

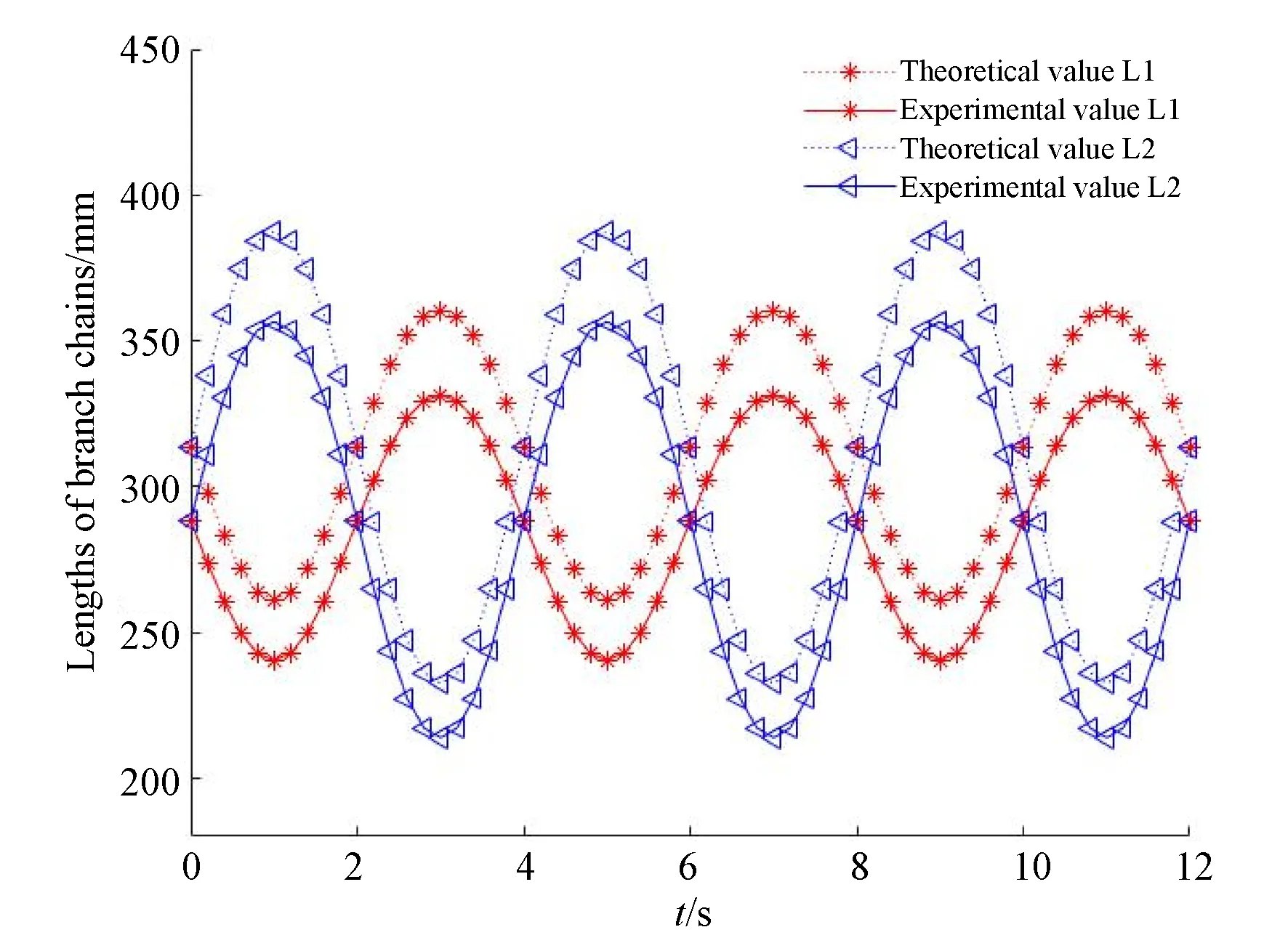
图15 实验中支链长度变化Fig.15 Variation curve of the length of branch chains in the experiment

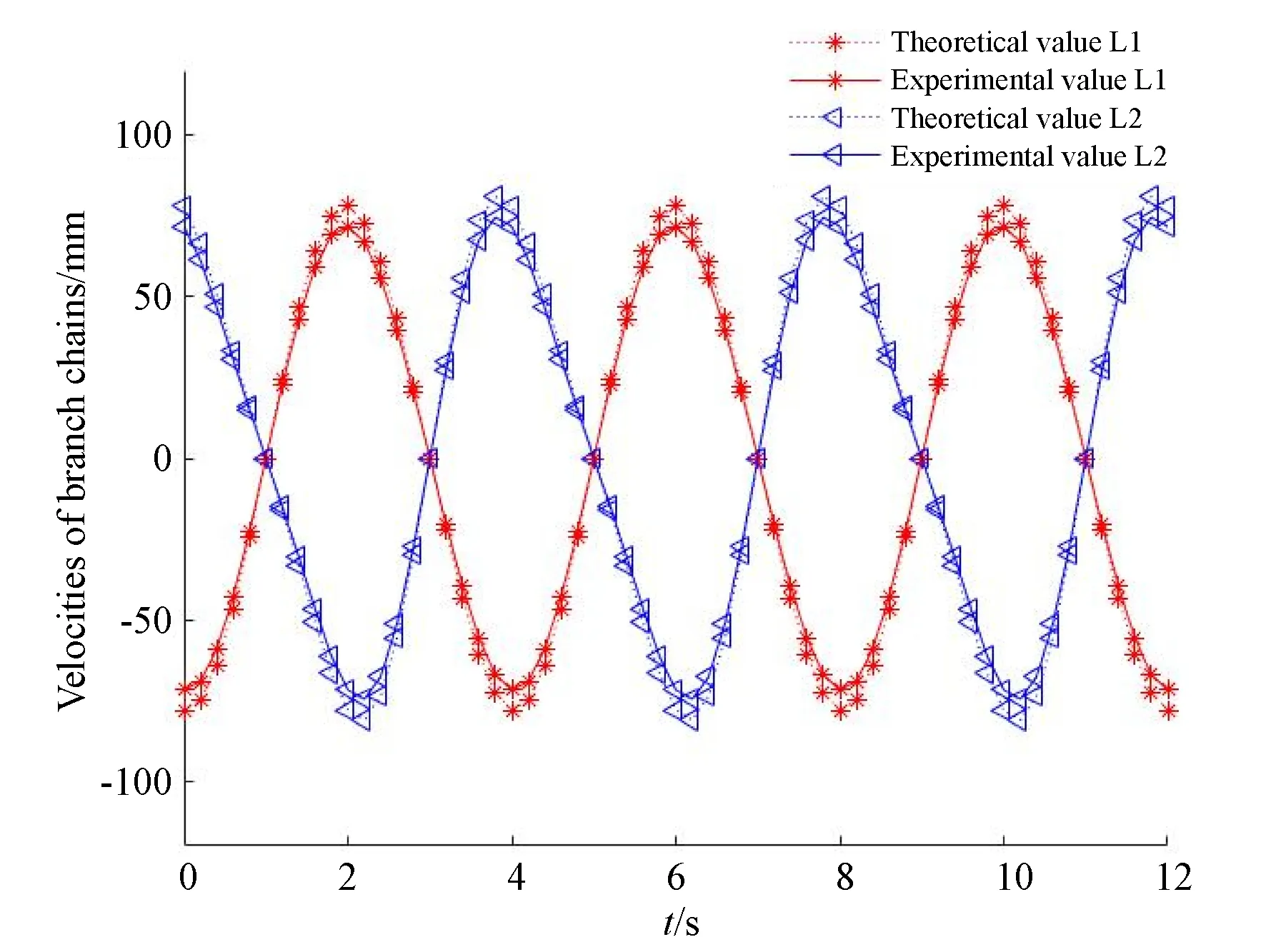
图16 实验中支链速度随时间的变化Fig.16 Variation of the velocity of branch chains with time in the experiment

5 结 论

根据水下机器人矢量推进的要求，首先，提出了一种UPR-UPU-UR矢量推进机构的设计方案。UPR-UPU-UR矢量推进机构不仅能够为水下机器人提供向前的推进力，而且主轴支链在纵向平面内可以灵活地偏转来改变螺旋桨的推进方向，实现偏航、俯仰、横滚等多种运动模式。经过位置建模，推导出该机构的位置反解表达式，然后，利用PSO算法验证了位置建模的正确性，各数值算例在动平台位姿绝对误差小于0.001°下获得机构动平台的精确位姿。紧接着使用数值搜索法分析，矢量推进机构动平台的工作空间是一部分球面。构建了机构中静平台与动平台之间的速度映射关系，最后搭建了UPR-UPU-UR矢量推进机构实验平台。经过数值仿真和实验验证表明，UPR-UPU-UR矢量推进机构的实际推进性能与理论设计存在误差最大为5%。UPR-UPU-UR矢量推进机构灵活性高，工作空间大，可以在狭小空间内实现多方向姿态摆动，有助于水下机器人在复杂海洋环境胜任作业任务。