基于构型演变和李群理论的2T2R型四自由度并联机构型综合

范彩霞 刘宏昭 张彦斌

1.西安理工大学,西安,710048 2.焦作大学,焦作,454150 3.河南科技大学,洛阳,471003

0 引言

少自由度并联机构是指自由度数为2～5的并联机构,适用于不完全需要六自由度的工作场合。除具有六自由度并联机构的优点外,少自由度并联机构还具有结构简单、设计制造成本低、控制容易等特点。因此,近十几年来,少自由度并联机构一直是国际机构学和机器人领域研究的热点之一。

在少自由度并联机构中,对具有2个移动和2个转动的2T2R型四自由度并联机构的研究相对较少,而2T2R型四自由度机构可直接作为四轴并联机床的原型,或者再串联一个自由度后可作为五轴混联机床或机器人的原型,也可开发为航海中船舶的减振装置[1]、农作物收获机上的振动筛[2]等,使空间2T2R型四自由度并联机构有着广泛的应用前景。

Li等[3]用约束螺旋法综合出一类对称2T2R型四自由度并联机构;杨廷力[4]用单开链单元法综合了一类2T2R型四自由度并联机构;文献[5-6]提出了一种2T2R型并联机构,并通过增加一个移动自由度开发了五轴联动并联机床;陈文家等[7]提出了2PRS-2PUS并联机构,Liu等[8-9]对该机构进行了工作空间等性能分析;汪劲松等[10]提出了几种2T2R型四轴并联机床结构;伞红军等[11]提出了2-TPR/2-TPS并联机构。

本文基于构型演变和李群理论,提出一类2T2R并联机构型综合的系统方法。从一个6R平面机构入手,将其中一个构件看作动平台,通过改变运动副,添加支链,演变成为空间并联机构2RRU-2SPS;然后基于李群理论找出等效支链,综合出一类2T2R并联机构。

1 理论基础

1.1 构型演变

构型演变[12]是并联机构型综合最直观、工程上最实用的方法。构型演变法发明新机构的基本思路是：以现成成功机构的原形为蓝本,通过各种不同的演化方法,如改变支链数目,改变支链中主动副的数目和类型,变换机架以及机架的布局形式等,得到满足特定需求的新机构。

传统的构型演变原则是,演变后的机构自由度不发生变化。本文中的构型演变原则是,将一个平面机构演变成一个空间机构,动平台增加了一个转动自由度。演变方法是,将与平面机构输出构件相连的两个R副改变为U副或S副,并改变输出构件形状,添加支链。

1.2 李群理论

根据群论,刚体在空间所有运动的集合D是李群,又称为位移群,则刚体在空间的大多数运动可以用D的子群表示,又称为位移子群。Herve[13]基于位移群的代数结构给运动链进行了分类,给出了全部12种位移子群,其中6种低副即转动副、移动副、螺旋副、圆柱副、球面副和平面副产生的位移集都是位移子群。

分支运动链末端相对于固定端的运动由所有低副生成的位移子群的乘积决定,这些位移子群的乘积可能仍然是位移子群,也可能是一个位移流形。

三维位移子群G(w)[14]表示法线为w的平面运动,即在垂直于w的平面内的2个移动和绕w的一个转动,根据位移子群乘积的封闭性和交换性,可得到G(w)的位移子群链和对应的运动链,如表1所示。表 1中,u、v、w表示正交的单位矢量,如vPwRwR表示2个R副轴线都平行于w,P副移动方向平行于v,2个R副轴线和P副移动方向垂直。

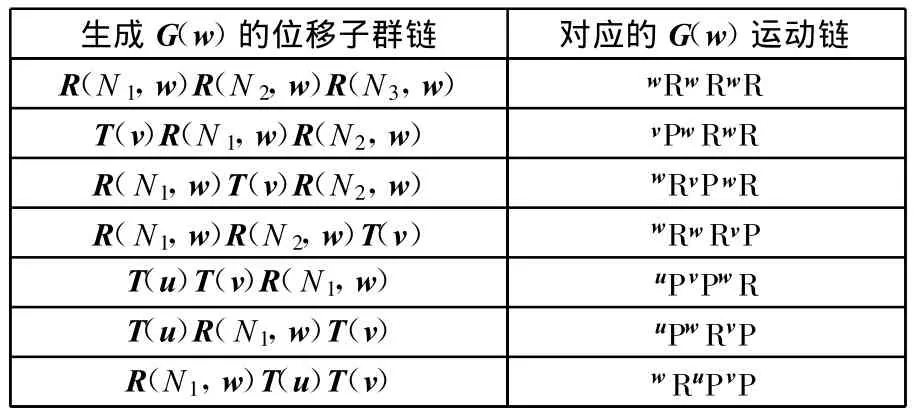
表1 G(w)的运动链

2 2T2R并联机构型综合

2.1 原机构分析

本文提出的2T2R空间并联机构是由一个三自由度平面机构增加一个转动自由度演变而来的,所以选择能产生2T1R平面运动的平面机构作为原机构。本文选择一个6R平面机构,如图1所示,选取OXYZ为固定坐标系。

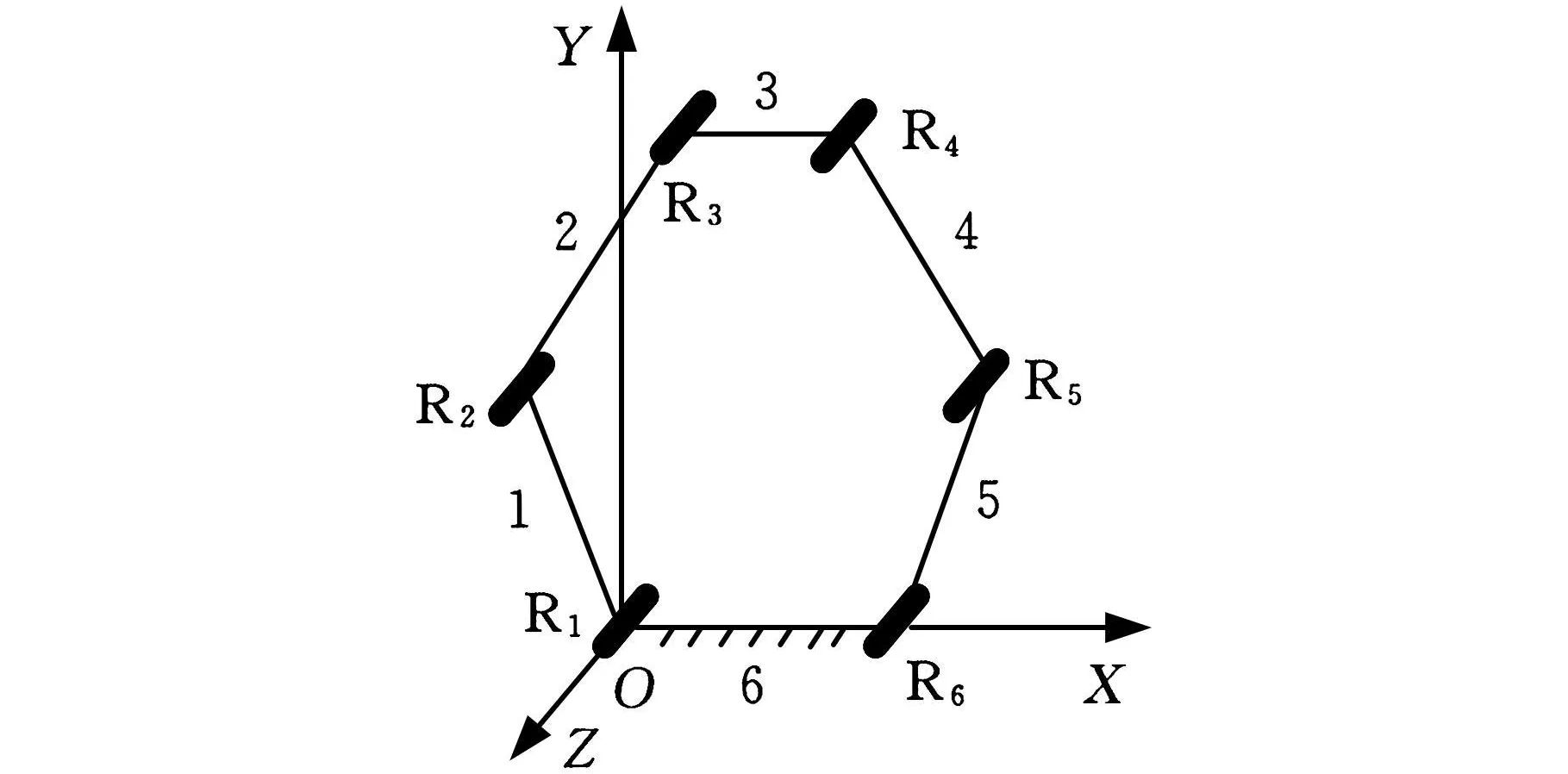
图1 平面6R机构

如果选取图1所示机构的构件3作为输出构件[15],则该机构就可看作具有2条对称支链的并联机构,2条支链分别为{-R1//R2//R3-}和{-R4//R5//R6-}。显然,构件3具有3个自由度,即沿X方向的移动、沿Y方向的移动、绕Z方向的转动。因此,选择输出运动为2T1R平面运动的构件作为动平台。

2.2 构型演变

(1)把构件3的两端换成U副。将图1中的构件3的两端换成U副,即R3换成U3,R4换成U4,U3副的一个轴线和原R3轴线同轴,另一个轴线和原R3轴线垂直,即沿构件3的轴线方向;U4副的一个轴线和原R4轴线同轴,另一个轴线和原R4轴线垂直,即沿构件3的轴线方向。显然,由于U3的一个轴线和U4的一个轴线共轴且沿构件3的轴线方向,所以构件3多了一个局部转动自由度,如图2所示。

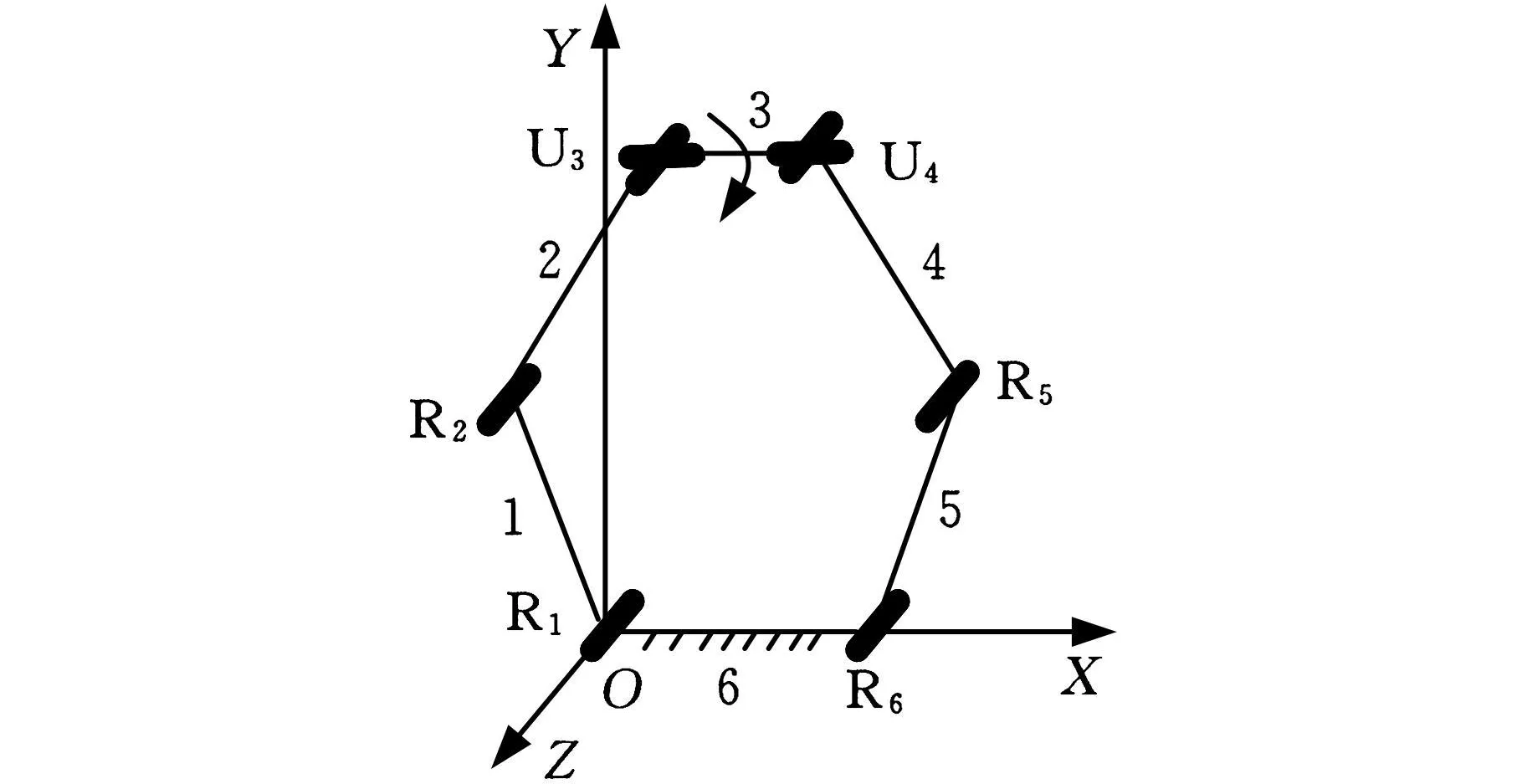
图2 构件3具有U副

(2)将构件3扩展成为一个平面,用一个长方形板表示,如图3所示,这个动平台就多了一个转动,具有2T2R型4个自由度,即沿X方向的移动、沿Y方向的移动、绕Z方向的转动和绕U 3 U4方向的转动。

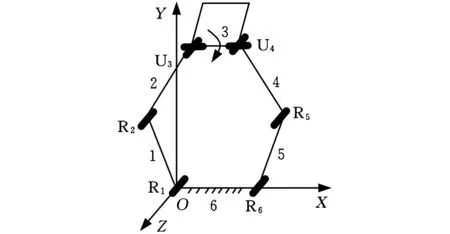
图3 构件3扩展为平面

(3)选用2个具有六自由度的运动链作为第三、第四支链,附加在长方形板上并将其支撑起来,支链的另一端与长方形静平台相连,图3中选用了常见的SPS支链作为第三、第四支链,由于自由度等于6的运动链为无约束支链[12],不对动平台产生约束,所以动平台的自由度不会发生改变,即得到2T2R型四自由度的新机构R1 R2 U 3-R6 R5 U 4-S7P8S9-S10P11S12,如图4所示。

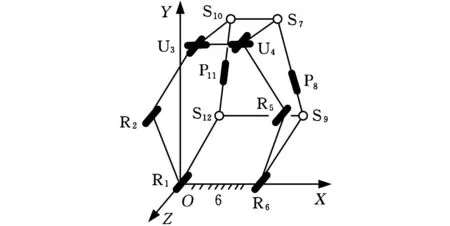
图4 R1R2 U3-R6 R5 U4-S7 P8 S9-S10 P11 S12机构

2.3 综合等效支链

上面所得到的2RRU-2SPS机构具有4个支链,分析各支链,运用李群理论找出等效运动链。由于第一支链和第二支链结构完全相同,第三支链和第四支链完全相同,所以只需要分析第一支链和第三支链。

第一支链{-R1//R2//U3-}的等效支链：

(1)原机构中的{-R1//R2//R3-}的等效支链。支链{-R1//R2//U3-}是由原机构中的{-R1//R2//R3-}演变而来的,而{-R1//R2//R3-}具有一个平面运动,即在OXY平面内的沿X、Y方向移动和绕Z的转动。因此,原机构中{-R1//R2//R3-}的等效支链必须具有平面运动。根据李群理论,具有平面运动的位移子群G(w)所对应的运动链有wRwRwR 、vPwRwR 、wRvPwR 、wRwRvP 、uPvPwR、uPwRvP、wRuPvP,见表1。并且上述运动链的末端只有是R副,才能在演变时被替换成U副。所以原机构中的{-R1//R2//R3-}的等效支链为可实现平面运动并且第三个运动副是 R副的运动链,有wRwRwR 、vPwRwR 、wRvPwR 、uPvPwR 。

(2){-R1//R2//U3-}的等效支链。如果原机构中构件3(图2)两端用S副代替U副,构件3也会具有一个局部自由度,再附加无约束运动链为第三、第四支链,这个局部自由度也会转化为动平台的一个有效自由度,和使用U副效果类似。因此,该支链的第3个运动副为S副或U副。所以,wRwRwR、vPwRwR、wRvPwR、uPvPwR 的第三个运动副被替换为 U副或者S副后,得出8种支链,再将其中的P副用平行四边形4R闭环代替,用Pa表示,又得出6种支链,结果如表2所示。表2中,Pa为平行四边形4R闭环,{-P(3S-2P)-P(3S-2P)-R(3S-2P)-S-}支链中的-P(3S-2P)-P(3S-2P)-R(3S-2P)-为3S-2P闭环的等效单开链,其他类似。

表2 2T2R机构等效支链

第三支链SPS的等效支链：

第三支链具备6个自由度,为无约束支链,无约束支链可由单开链法、约束螺旋法、李群理论来产生,本文参考了文献[4,12],选用了常见的支链 ：SPS、PSS 、RSS 、PUS 、UPS 、RUS 、RRRRRR、RRRRRP、RRRRPP、RRRPPP,含有闭环的支链有{-P(3S-2P)-P(3S-2P)-R(3S-2P)-S-}、{-P(3S-2R)-P(3S-2R)-R(3S-2R)-S-}、{-P-P(3R-2P)-P(3R-2P)-S-}、{-R(3S-2P)-P(3S-2P)-P(3S-2P)-S-}、{-R(3S-2R)-P(3S-2R)-P(3S-2R)-S-}[4],如表2所示。

2.4 构造2T2R机构

2.4.1 选取支链

从表2中,选出4个支链：第一、第二支链的等效支链中任意选2个,第三、第四支链的等效支链中任意选2个。可得出这4种情况：第一、第二支链相同,且第三、第四支链相同的有14×15=210种机构,如 2RPU-2SPS;第一、第二支链相同,且第三、第四支链不同的有14C215=1470种机构,如2RPU-SPS-UPS;第一、第二支链不同,且第三、第四支链相同的有15C214=1365种机构,如RPU-RPS-2SPS;第一、第二支链不同,且第三、第四支链不同的有=9555种机构,如 RRURRS-SPS-UPS。

2.4.2 配置支链

在支链装配时,为达到期望的自由度,配置支链的原则是,由原6R机构演变而来的2条支链要共面并且各转动副互相平行且垂直于该面。

对于支链选取的4种情况中,前3种情况的机构中都有相同的支链。对于有相同支链的机构,相同支链可以采取相邻分布和对角分布两种配置形式,理论上可以得出210×2+1470×2+1365×2+9555=15 645种 2T2R型四自由度机构。

在这些机构中,第一、第二支链相同、且第三、第四支链相同的机构具有最大程度的对称性,选出其中典型的新机构,如图5中的2RPU-2SPS机构、图 6中的 2PRU-2PUS机构、图 7中的2PRU-2RSS机构。

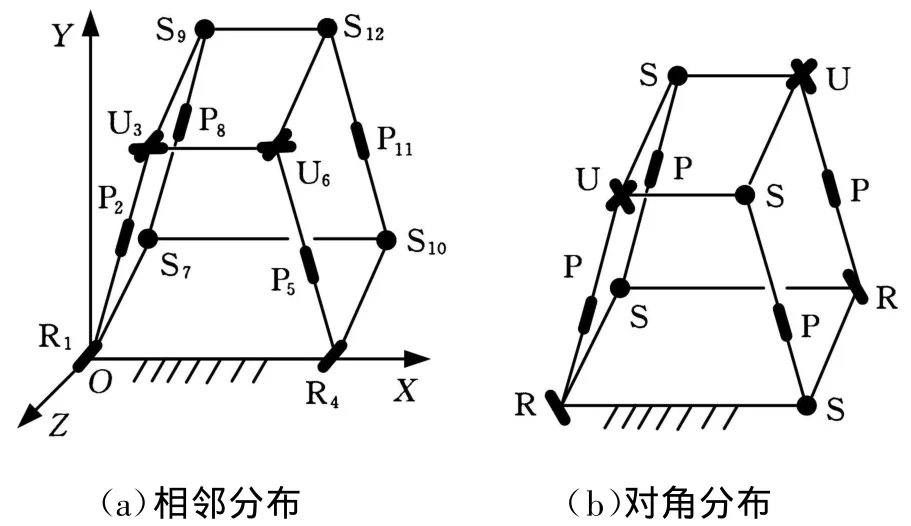
图 5 2RPU-2SPS机构

图6 2PRU-2PUS机构

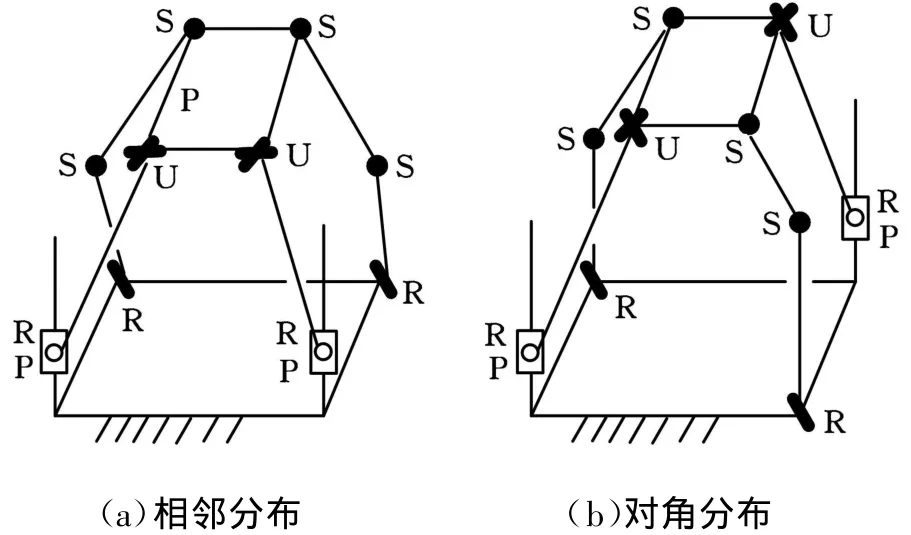
图7 2PRU-2RSS机构

3 2RPU-2SPS机构的自由度计算和主动副选取

任意选取一新机构2RPU-2SPS,如图5a所示,运用单开链法计算其自由度和确定其主动副。

该机构由 4条单开链(single open chain,SOC)组成,其结构为SOC{-R1⊥P2⊥U 3-}、SOC{-R4 ⊥P5 ⊥U6-}、SOC{-S7-P8-S9-}、SOC{-S10-P11-S12-}。

基于单开链法计算机构活动度为

式中,F为机构活动度;fi为运动副的自由度;m为运动副数;ξj为第j个基本回路的独立位移方程数。

对于该机构,4条单开链的自由度数分别为4、4、6、6,满足∑ξj为最小值,它的3个基本回路分别为{-R1(⊥P2)//R31⊥R32/R61⊥R62(⊥P5)//R4-},ξ1=4;{-R1(⊥P2)//R31⊥R32-S7-P8-S9},

其中,R⊥R表示U副用2个垂直的R副代替。

若取P2、P5、P8、P11为主动副并刚化之,刚化后的机构活动度为

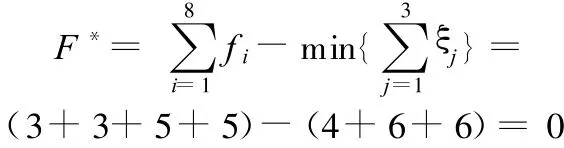
其中,满足 ∑ξj为最小值时,它的3个基本回路分别为{-R1//R31⊥R32/R61⊥R62//R4-},ξ1=4;{-R1//R31⊥R32-S7-S9},ξ2=6;{-S7-S9-S12-S10-},ξ3=6。

因为F*=0,满足主动副存在准则,故4条支链上的移动副P2、P5、P8、P11可同时为主动副。

上述分析表明本文所提出的基于构型演变和李群理论的2T2R型四自由度并联机构的型综合方法正确可行。

4 结论

(1)基于构型演变法,提出了一种新的机构2RRU-2SPS,机构具有2个相邻的RRU支链和2个相邻的SPS支链。

(2)在2RRU-2SPS机构的基础上,运用构型演变和李群理论寻找等效支链,综合出15 645种2T2R机构。

(3)选取典型新机构2RPU-2SPS,分析其自由度和确定主动副,同时也验证了本文提出的综合方法的正确性。

[1] 马履中,陈修祥,杨启志,等.基于并联机构的具有冗余自由度四自由度弹性阻尼减振装置研究[J].中国机械工程,2006,17(17)：1761-1764.

[2] 刘剑敏,马履中,许子红,等.振动筛两平移两转动并联机构的运动学分析[J].农业机械学报,2008,39(2)：14-17.

[3] Li Qinchuan,Huang Zhen.Type Synthesis of 4-DOF Parallel Manipulators[C]//Proceedings of the 2003 IEEE International Conference on Robotics&Automation.Taipei：Institute of Electrical and Electronics Engineers Inc.,2003：755-760.

[4] 杨廷力.机器人机构拓扑结构学[M].北京：机械工业出版社,2003.

[5] Chen Wenjia,Zhao Mingyang,Chen Shuhong,et al.A Novel 4-DOF Parallel Manipulator and Its Kinematic Modelling[C]//Proceedings of the 2001 IEEEInternational Conference on Robotics&Automation.Seoul：Institute of Electrical and Electronics Engineers Inc.,2001：3350-3355.

[6] 陈文家,赵明扬,房立金,等.基于四自由度并联机构的数控机床研究[J].扬州大学学报,2001,4(2)：50-54.

[7] 陈文家,陈书宏,张波.一种四自由度并联机构及其运动学建模[J].机械设计,2001(10)：6-8.

[8] Liu Hongjun,Liu Bin,Sun Cuilian.Calibration of a4-DOF Parallel Manipulator[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation.Piscataway：Institute of Electrical and Electronics Engineers Inc.,2006：7958-7962.

[9] Liu Hongjun,Qin Yongfa,Zhao Mingyang.The Reachable Workspace Analysis of a Kind of 4-DOF Parallel Mechanism Based on Constraints[C]//Proceedings of the 2003 IEEE International Conference on Robotics,Intelligent Systems and Signal Processing.Changsha：Institute of Electrical and Electronics Engineers Inc.,2003：799-803.

[10] 汪劲松,刘辛军,段广洪,等.两维移动两维转动四轴并联机床结构：中国,00105936[P].2000-09-27.

[11] 伞红军,钟诗胜,王知行.新型 2-TPR/2-TPS空间四自由度机构并联机构[J].机械工程学报,2008,36(11)：298-303.

[12] 于靖军,刘辛军,丁希仑,等.机器人机构学的数学基础[M].北京：机械工业出版社,2008.

[13] Herve JM.The Lie Group of Rigid body Displacements,a Fundamental Tool for Mechanism Design[J].Mechanism and Machine Theory,1999,34(5)：719–730.

[14] Lee C C,Herve J M.Translational Parallel Manipulators with Doubly Planar Limbs[J].Mechanism and Machine Theory,2006,41(2)：433-455.

[15] Zeng Daxing,Huang Zhen,Lu Wenjuan.A family of Novel 2 DOF Rotational Decoupled Parallel Mechanisms[C]//Proceedings of the 2007 IEEE International Conference on Mechetronics and Automation.Piscataway：Inst.of Elec.and Elec.Eng.Computer Society,2007：2478-2483.