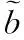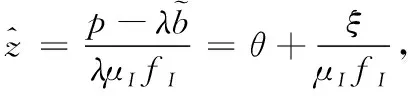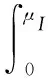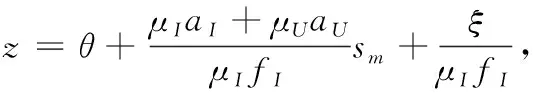异质信念下内幕交易者市场操纵行为研究
周 奇,尤左伟,刘善存,韩景倜
(1. 上海财经大学信息管理与工程学院,上海 200433;2. 北京航空航天大学经济管理学院,北京 100191)
1 引言
市场操纵行为是指市场操纵人利用掌握的资金、信息等优势,采用不正当手段,人为制造证券行情,操纵或影响证券市场价格,以诱导证券投资者盲目进行证券买卖,从而为自己牟取利益或转嫁风险的行为。市场操纵行为扰乱证券市场秩序,损害广大投资者利益,妨碍证券市场健康发展,被明令禁止。《禁止证券欺诈行为暂行办法》给出了八种市场操纵行为的具体形式,包括“通过合谋或者集中资金操纵证券市场价格、以散布谣言等手段影响证券发行和交易、虚买虚卖、连续交易”等。据报道,近年来证监会每年立案调查几十起市场操纵案件,其中多起涉嫌编造、传播虚假证券信息及非法经营证券业务,并且不少是通过媒体、网络平台编造、传播公司并购重组虚假信息,影响股价后趁机获利。
关于市场操纵行为的学术研究可追溯到二十世纪八九十年代,近30年来学术界对该领域保持着高度关注。一方面,Allen和Gale(1992)[1]将股票市场操纵行为分为基于行动的操纵、基于信息的操纵和基于交易的操纵,并在理性预期框架下研究市场操纵行为。其中基于行动的市场操纵可参阅Vila(1989),基于信息的市场操纵可参阅Vila(1989)[2]、Benabou和Laroque(1992)[3],基于交易的市场操纵可参阅Allen和Gale(1992)[1]、Jarrow(1992)[4]、Fishman和Hagerty(1995)[5]。刘元海等(2002)[6]、夏昕阳和杨之曙(2004)[7]对这三类操纵行为的理论与实证研究作了总结性评述。另一方面,市场操纵根据操纵者是否知情又可分为两种情形:知情者操纵价格、非知情者假装成知情者去操纵价格。国内外文献关于知情者操纵行为的研究很多,例如Bommel (2003)[8]的理论研究、张宗新和沈正阳(2007)[9]的实证研究,等。Allen和Gorton(1992)[10]、Fishman和Hagerty(1995)[5]、Goldstein和Guembel(2010)[11]都涉及了非知情者操纵市场价格并获利的可能性及具体操作情况。Chakraborty和Yilmaz(1999)[12]、曾庆铎等(2017)[13]对知情者操纵、非知情者操纵两种情形都做了理论研究。近两年来国内对信息型市场操纵的研究热度不减。沈冰和周杰(2017)[14]通过理论建模分析了知情交易者与监管部门之间博弈关系的策略,提出监管部门要加大力度处罚内幕信息操纵行为的建议。钟廷勇等(2017)[15]通过建模对股价异动和市场操纵行为进行理论分析后指出,在被操纵期间,股票价格将会不断上升,而当真实的股票价值被揭示时,股票价格将会下降,并给出监管建议。徐龙炳等(2018)[16]系统总结分析了信息型市场操纵及其经济后果、监管等方面的文献后指出,信息型市场操纵会损害资本市场资源配置功能,并损害投资者权益。
此外,由于投资者在认知上都有局限,在心理上都有情感,在立场上都有偏向,所以不同投资者对同一证券的价值具有不同的看法。将市场参与者异质信念引入到传统的资产定价理论中,能很好地解释传统资产定价理论不能解释的某些金融市场异象。到目前为止国内外已有大量文献专注于投资者异质信念下资产定价的理论与实证研究,例如Miller(1977)[17]、刘善存等(2013)[18]、Shi(2016)[19]的理论研究,包锋和徐建国(2015)[20]、朱宏泉等(2016)[21]对中国股市的实证研究。
然而到目前为止,作者还未能搜索到关于市场操纵理论研究的文献考虑了投资者异质信念。本文的理论研究将围绕投资者异质信念是否会影响市场操纵者行为这个问题而展开。本文将投资者对证券清算价值的看法与其实际值的差别称为投资者的信念偏差(也称为看法偏差),将投资者信念偏差引入到市场操纵模型中,借助于金融市场微观结构理论[22],在竞争性理性预期均衡的框架下[23],建立起关于非知情交易者异质信念下内幕交易者市场操纵策略的模型,聚焦于非知情交易者信念偏差对内幕交易者市场操纵行为的影响。这里市场操纵行为表现为市场操纵人借助于自己的信息优势散布谣言,故意诱导广大投资者对证券价格走势产生错判,从而达到抬高或压低价格的目的,最终自己趁机获取利益。此设置的合理性如下:第一,我国证券市场法律制度还不够完善,违法成本较低,投资者中散户占比高,也容易被诱导,故而操纵人利用信息优势操纵价格的行为在中国证券市场也容易奏效。第二,目前关于我国内幕交易者的策略选择研究,对我国内幕交易者更倾向于采取隐蔽策略还是更倾向于采取操纵策略,尚无定论,本文中内幕交易者采取操纵策略的设置并不会与以往的研究相冲突。第三,非知情者只能通过观察市场价格预判清算价值,所以可预期非知情者的信念偏差对均衡价格有较大影响,而知情者既然已经拥有关于清算价值的信息,研究其信念偏差对均衡价格影响意义偏小。第四,徐龙炳等(2018)[16]同时指出,目前无论理论界还是实务界对信息型市场操纵甚至市场操纵本身的认知都还十分模糊,还未解决对其操纵手法及完整信息型市场操纵链条的解释。因此,本文依托建模试图从底层探讨信息型市场操纵手法,丰富这一理论,具有创新性。
2 非知情者异质信念下的基准模型
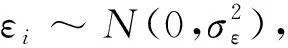
非知情交易者不能观察到信号si,不妨记非知情交易者的信息集为{p},非知情乐观交易者和非知情悲观交易者都基于价格信息{p}进行交易,但是他们对清算价值的看法不一样,假设非知情乐观交易者(用j表示)与非知情悲观交易者(用k表示)对清算价值的看法分别为:
(1)
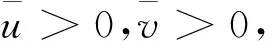
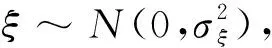
现在假设所有交易者的初始禀赋均为0;所有交易者均为风险厌恶型,效用函数是常数绝对风险厌恶系数型(CARA)的,形如U(π)=-e-ρπ,这里π表示收益。对于知情交易者ρi=ρI>0,非知情乐观交易者ρj=ρO>0,非知情悲观交易者ρk=ρP>0,有时候也将风险厌恶系数的倒数称为风险承受系数。现在我们建立如下两期模型。
在期初,知情交易者i购买xi单位风险资产,他认为在期末将获得的回报为πi=(θ-p)xi,其效用函数为Ui(πi)=-e-ρiπi。同理,在期初,非知情乐观交易者j和非知情悲观交易者k分别购买xj和xk单位风险资产,两者认为在期末将获得的回报分别为πj=(θO,j-p)xj和πk=(θP,k-p)xk,效用函数分别为Uj(πj)=-e-ρjπj和Uk(πk)=-e-ρkπk。
记知情交易者i∈[0,μI]的交易需求为XI(si,p),非知情乐观交易者j∈(μI,μI+μO]的交易需求为XO,j(p),非知情悲观交易者k∈(μI+μO,1]的交易需求为XP,k(p),一个理性预期均衡是依赖于交易者拥有信息的一组交易集合:
{XI(si,p),i∈[0,μI];XO,j(p),j∈(μI,μI+μO];
XP,k(p),k∈(μI+μO,1] }
以及一个价格函数p(θ,ξ),满足以下两个条件:
条件1市场出清:
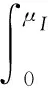
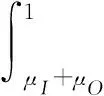
(2)
条件2交易者效用函数值最大化:
XO,j(p):=XO(uj,p)∈
XP,k(p):=XP(vk,p)∈
(3)
市场出清方程可以理解为噪声交易者为知情交易者和非知情交易者提供流动性,此时为供需出清。若方程(2)和方程组(3)存在单一解,称市场存在单一均衡;若存在多个解,则称市场存在多重均衡。
基于理性预期理论,经计算可得如下定理1。
定理1设ρI>0,ρO>0,ρP>0。上述金融市场存在唯一的贝叶斯线性均衡,在这个线性均衡中,对价格p(θ,ξ)的需求函数为:
XI(si,p)=fIsi-gIp+cI
(4)
XO(uj,p)=fOuj-gOp+cO
(5)
XP(vk,p)=-fPvk-gPp+cP
(6)
其中,
(7)
(8)
(9)
这里,
(10)
(11)
τ=τθ+τξ(μIfI)2
(12)
并且均衡价格函数为:
(13)
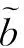
λ=[μIgI+μOgO+μPgP]-1,
(14)
注1这里λ-1表示市场深度,由定理1可知非知情交易者的信念偏差对与市场深度没有影响,其影响的是非知情交易者和知情交易者的交易需求以及风险资产的均衡价格。
现在讨论非知情交易者的信念偏差对均衡价格的影响。根据定理1,可得:
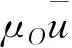
3 非知情者异质信念下的简化模型
这里不考虑非知情交易者的分类,其他都与基准模型一样。记非知情交易者(用j∈(μI,1]表示)对清算价值的看法为:
其中wj与θ相互独立。
在期初,非知情交易者j购买xj单位风险资产,他认为在期末将获得的回报为πj=(θU,j-p)xj,其效用函数为Uj(πj)=-e-ρjπj。
同理,记非知情交易者j∈(μI,1]的交易需求为XU,j(p),则根据理性预期均衡的两个条件:
条件1市场出清:
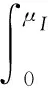
(15)
条件2交易者效用函数值最大化:
XU,j(p):=XU(wj,p)∈
(16)
我们可以得到如下定理2。
定理2设ρI>0,ρU>0。上述金融市场存在唯一的贝叶斯线性均衡,在这个线性均衡中,对价格p(θ,ξ)的需求函数为:
XI(si,p)=fIsi-gIp+cI
(17)
XU(wj,p)=fUwj-gUp+cU
(18)
其中,
(19)
(20)
(21)
并且均衡价格函数为:
(22)
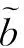
(23)
注2定理2的证明过程和定理1的类似,此处略。为了保持形式上的一致性,定理2和定理1中相对应的系数用相同的字母表示,我们有理由相信这并不会引起混淆,以下亦然。
根据定理2,可得:
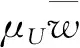
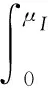
由上式可知,知情交易者的人均交易需求与非知情交易者的整体信念偏差呈线性负相关。
由上式可知,非知情交易者的人均需求与非知情交易者的人均信念偏差呈线性正相关。可作如下理解:当非知情交易者的整体信念偏差增大时,非知情交易者的交易需求增加,从而价格上升,继而知情者的交易需求减小;反之亦然。
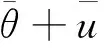
4 内幕交易者市场操纵下的线性均衡
本小节开始讨论在内幕交易者进行市场操纵情况下的线性均衡问题。我们基于上述的简化模型作扩展研究。假设知情交易者中有一位神通广大的内幕者,他获得更精确的内幕信息并操纵市场,这里也称之为市场操纵者,具体如下:
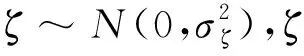
(24)
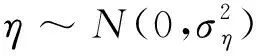
(1)对于非知情交易者,价格不会包含比信号sm,j更多关于sm的信息,所以非知情交易者的需求函数为:
(25)
(2)对于知情交易者,其需求函数为:
(26)
由于操纵者仅有一位而其他交易者用连续统表示,从而操纵者的交易量对价格影响可以忽略不计,即操纵者对价格的影响是通过价格信息操纵而非交易量操纵。基于理性预期理论,经计算可得如下定理3。
定理3设ρI,ρU,ρM>0。上述金融市场在内幕交易者的操纵下,可能存在贝叶斯线性均衡,在这个线性均衡中,非知情交易者和知情交易者对价格p(sm,θ,ξ)的需求函数分别为:
XU(sm,j,wj,p)=aUsm,j+fUwj-gUp+cU
(27)
XI(sm,i,si,p)=aIsm,i+fIsi-gIp+cI
(28)
其中,
(29)
(30)
(31)
这里,
(32)
(33)
并且均衡价格函数为:
p(sm,θ,ξ)=λ[μIfIθ+ (μIaI+μUaU)sm
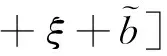
(34)
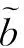
(35)
市场是否存在线性均衡,取决于方程(30)是否有实根:如果方程(30)仅有一个实根,则存在唯一线性均衡;如果方程(30)存在两个或三个实根,则存在多重线性均衡。
注4关于aI的方程(30)等价于:
(36)
现在,为了便于分析,不妨作如下假设。
假设1知情交易者的比例远小于非知情交易者的比例,即
μI≪μU
(37)
该不等式的合理性在于,能获得真实消息的投资者在市场中的比例确实很低。
假设2
|aI|<|aU|
(38)
将该不等式作为假设2仅仅只是为了形式上的对称,事实上该条件是必然成立的,原因如下:由于非知情交易者j是基于sm+wj-p进行交易,所以XU对sm的变动非常敏感;而知情交易者i是基于θ-p进行交易,所以XI对sm的变动并不敏感。假设当前时刻θ*>p,市场操纵者会买入股票,此时他会散布谣言称清算价值很低,从而引导非知情交易者卖出股票,使得股票价格降低,此时知情交易者会买入股票。如果sm下降,则XU会随之下降,从而价格p降低,这样知情交易者的需求XI会上升,传导关系如下:
sm↓⟹XU↓⟹p↓⟹XI↑(ifθ*>p)
反之,假设当前时刻θ* sm↑⟹XU↑⟹p↑⟹XI↓(ifθ* 从传导机制角度看,关于清算价值的假消息sm对XU是直接影响,而对XI是间接影响,从而|aI|<|aU|,并且由以上分析可知aU>0,aI<0。 在假设1与假设2成立的情况下,有|μIaI|≪|μUaU|,则方程(36)有近似解: (39) 此时,市场存在唯一的线性均衡。这样,我们可以得到如下推论1。 推论1设ρI,ρU>0,μI≤μU,|aI|<|aU|,则上述金融市场在内幕交易者的操纵下,存在唯一的关于线性价格泛函p(sm,θ,ξ)的需求函数的贝叶斯线性均衡。这个均衡是: XU(sm,j,wj,p)=aUsm,j+fUwj-gUp+cU XI(sm,i,si,p)=aIsm,i+fIsi-gIp+cI 其中,aI如式(39)所示, 这里, 并且均衡价格为: 注5根据推论1可得: (40) 假消息对均衡价格的影响与市场深度的倒数、信息传播误差、非知情交易者的比例及其风险承受系数密切相关。当知情交易者的比例远小于非知情交易者的比例时,这种相关是线性正相关。 基于推论1,可以讨论内幕交易者的市场操纵策略。 由于Y的值随着(θ*-p)2的增大而增大,所以对Y的讨论可转变为对(θ*-p)2的讨论。定义 y(sm):=(θ*-p)2 (41) 则dy/dsm=-2(θ*-p)λ(μIaI+μUaU)。 结合式(41)和推论1可得如下结论: 如果将所有非知情交易者作为一个整体,对非知情交易者而言,整体损益为: (42) 非知情交易者的人均损益为: (43) 同理,如果将除操纵者外的所有知情交易者作为一个整体,对知情交易者而言,整体损益为: =μI(θ-p)(aIsm+fIθ-gIp+cI) (44) 知情交易者的人均损益为: (θ-p)(aIsm+fIθ-gIp+cI) (45) 图1 均衡价格p随着变动的图形(bias表示 即非知情交易者的人均信念偏差提高1单位,均衡价格将提高0.559单位。 图2 人均交易需求随着变动的图形(bias表示 图3 均衡价格p随着sm变动的图形(bias表示 ∂p/∂sm=λ(μIaI+μUaU)=0.8856。 图4 y(sm)随着sm变动的图形(bias表示 根据式(44)可得对应的知情交易者的整体损益为: ΠI=μI(θ-p)(aIsm+fIθ-gIp+cI) 对比以上两式可知,非知情交易者的整体损失是知情交易者的整体收益。值得注意的是,有此结论的前提是:交易者用连续统[0,1]表示,噪声交易者的交易量净值为零。 通过以上的模型和数值算例的展示,我们能很好地理解内幕交易者借助于自身的信息优势以及个人影响力,进行基于信息的市场操纵行为。这个模型展示了内幕交易者基于信息进行操纵的两种方式: (1)通过散布谣言诱导非知情交易者卖出股票而压低价格,自身却趁机买入股票获利; (2)通过散布谣言诱导非知情交易者买入股票而抬高价格,自身却趁机卖出股票获利。 打击市场操纵是监管机构的职责之一,甄别市场操纵行为是打击市场操纵的前提。基于本文的理论研究,运用大数据技术与金融科技,对监管机构甄别市场操纵行为有如下启示:如果对某只股票具有影响力的某行为人(比如公司高管、证券分析师或媒体大咖),在媒体、网络平台散布一则关于该股票的好(或坏)消息,使得该股票价格在短时间内大幅度上涨(或下跌),而与其有密切关系的某些账户却在大量卖出(或买入)该股票;一段时间后,关于该公司的私人消息公布使得该股票价格大幅度下跌(或上涨),则可初步认为该行为人涉嫌市场操纵。 建议抓住智能化革命的契机,基于互联网、大数据等技术,运用金融科技的力量为监管赋能,有效识别市场操纵行为,强化市场监管,严惩市场操纵行为,维护广大投资者的利益,维护股票市场的行稳致远。 本文以金融市场微观结构为视角,基于竞争性理性预期均衡的框架,建立非知情交易者异质信念下风险资产定价模型,推导出关于风险资产的贝叶斯线性均衡价格,并基于此研究内幕交易者的市场操纵行为,得出如下结论。 第一,非知情交易者的信念偏差对交易需求、均衡价格以及内幕交易者的操纵策略都具有重大影响,具体表现如下:如果非知情交易者的信念偏差增大,则非知情交易者的需求随之增加而导致价格升高,继而知情交易者的需求减少;反之,如果非知情交易者的信念偏差减小,则非知情交易者的需求随之减少而导致价格降低,继而知情交易者的需求增加。第二,非知情交易者的信念偏差对市场深度没有影响。第三,在线性均衡下,均衡价格与内幕交易者散布的虚假消息呈线性正相关,虚假消息对非知情交易者的影响程度远大于对知情交易者的影响程度。第四,内幕交易者在进行市场操纵时,需要充分考虑非知情交易者的整体信念偏差。第五,内幕交易者通过散布虚假消息使得非知情交易者成为虚假消息的跟随者,由于非知情交易者比例远大于知情交易者的比例,从而非知情交易者成为虚假消息的跟随者后,改变了其交易需求并影响了价格,使得价格朝着有利于操纵者的方向变动,操纵者则趁机获利。 本文通过建模研究了内幕交易者的市场操纵行为,一是揭示了内幕操纵严重损害了广大非知情投资者的利益,阻碍了资本市场的健康发展,二是为监管机构甄别市场操纵提供了理论依据。建议运用金融科技为监管赋能,有效增强识别市场操纵行为的能力。 本文的模型可以在以下方面进行深入研究。第一,本文讨论的是知情交易者市场操纵的情形,可以继续讨论非知情交易者的市场操纵策略。第二,本文的模型是“0-1”两期模型,可以进一步建立“0-1-2”三期模型,深入研究虚假消息与真实信息共同作用下价格形成机制,并基于此研究投资者异质信念对操纵策略的影响。 附录: 1 定理1的证明 证明:将式(4-6)代入式(2)可得: 根据交易者效用函数值最大化条件,可得: (A1) (A2) (A3) 将以上两式代入式(A2)可得式(8),将以上两式代入式(A3)可得式(9)。另外, 将以上两式代入式(A1)可得式(7)。再将式(7-9)代入式(14)计算可得式(10-11),证毕。 2 定理3的证明 证明:先假设存在唯一的贝叶斯线性均衡。根据市场出清条件: 可得: 其中,随机变量z在信息上与价格p等价,将sm=sm,i-ηi代入z并记: 则随机变量(zi,z)在信息上与(sm,i,p)等价,所以我们有: Var[θ|p,sm,i,si]=Var[θ|z,zi,si]=Var[θ|zi,si] E[θ|p,sm,i,si]=E[θ|z,zi,si]=E[θ|zi,si] 这里,第二个等号成立的原因是zi比z包含的关于θ的信息更多。根据投影定理可得: (Var[θ|sm,i,si,p])-1=(Var[θ|zi,si])-1 以及 E[θ|sm,i,si,p]=E[θ|zi,si] 将上面两个式子代入XI(sm,i,si,p)并整理可得式(30-31),结合式(35)可计算得式(32),证毕。5 内幕交易者的市场操纵策略
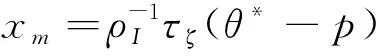
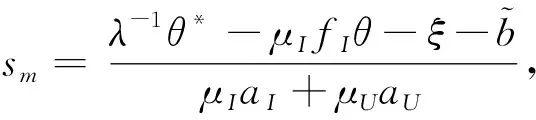
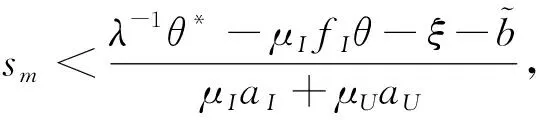
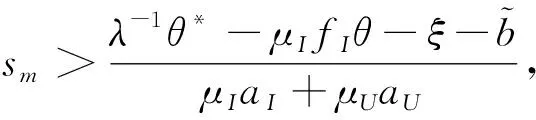
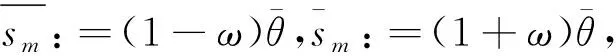
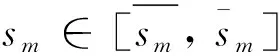
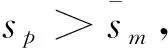
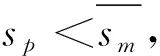
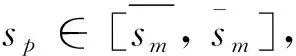
6 数值算例与讨论
6.1 信念偏差对均衡的影响
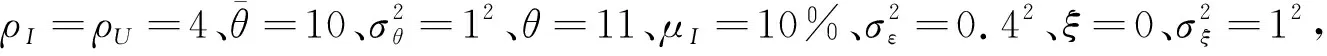
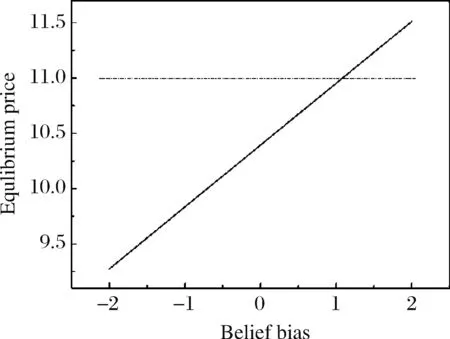
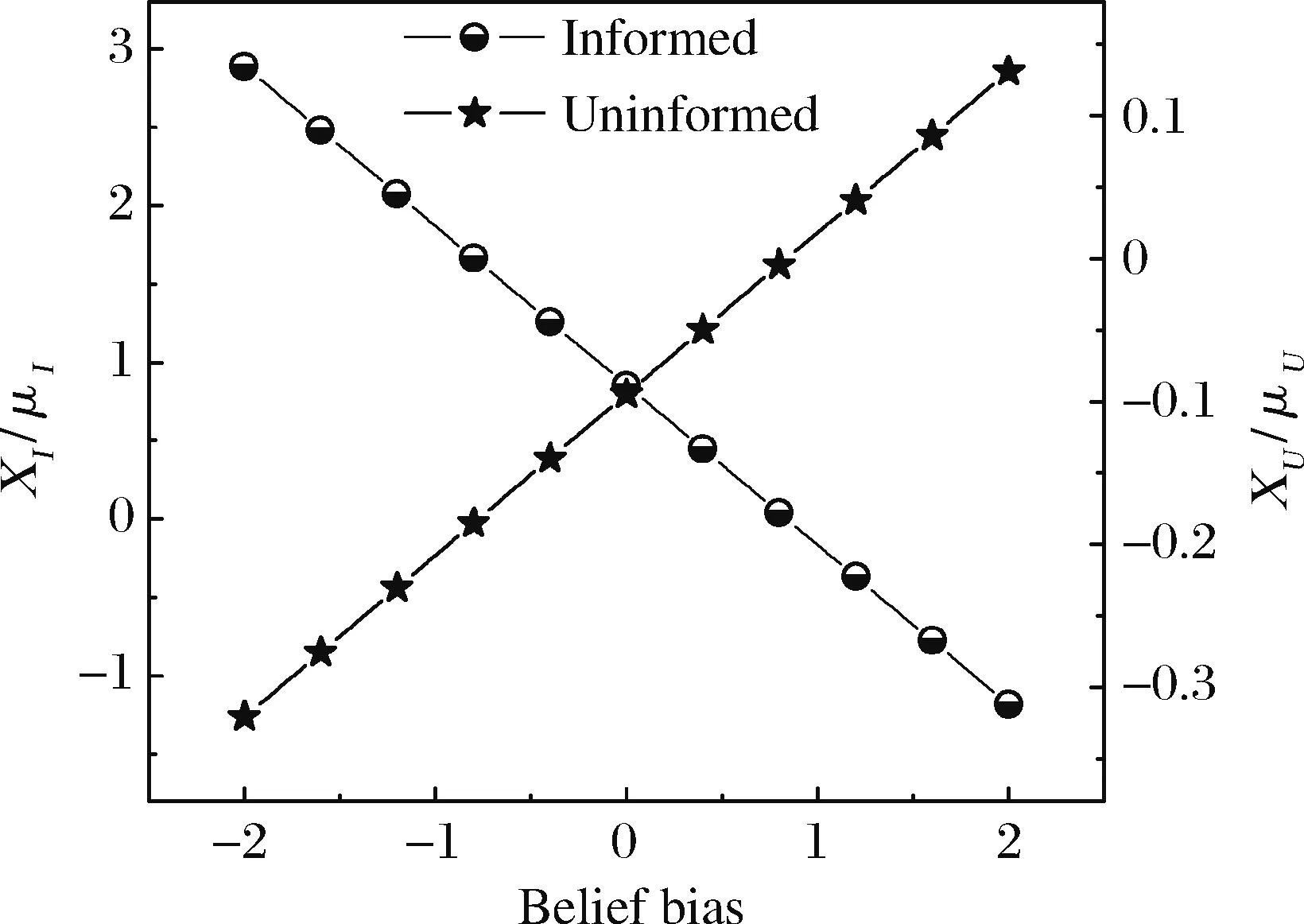
6.2 假消息对均衡价格的影响
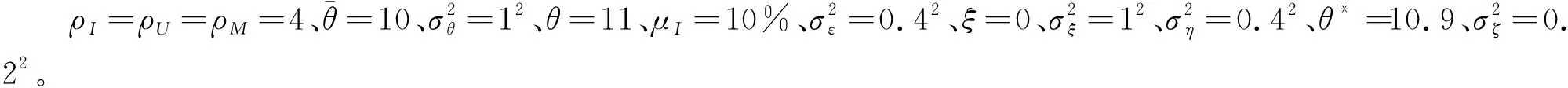
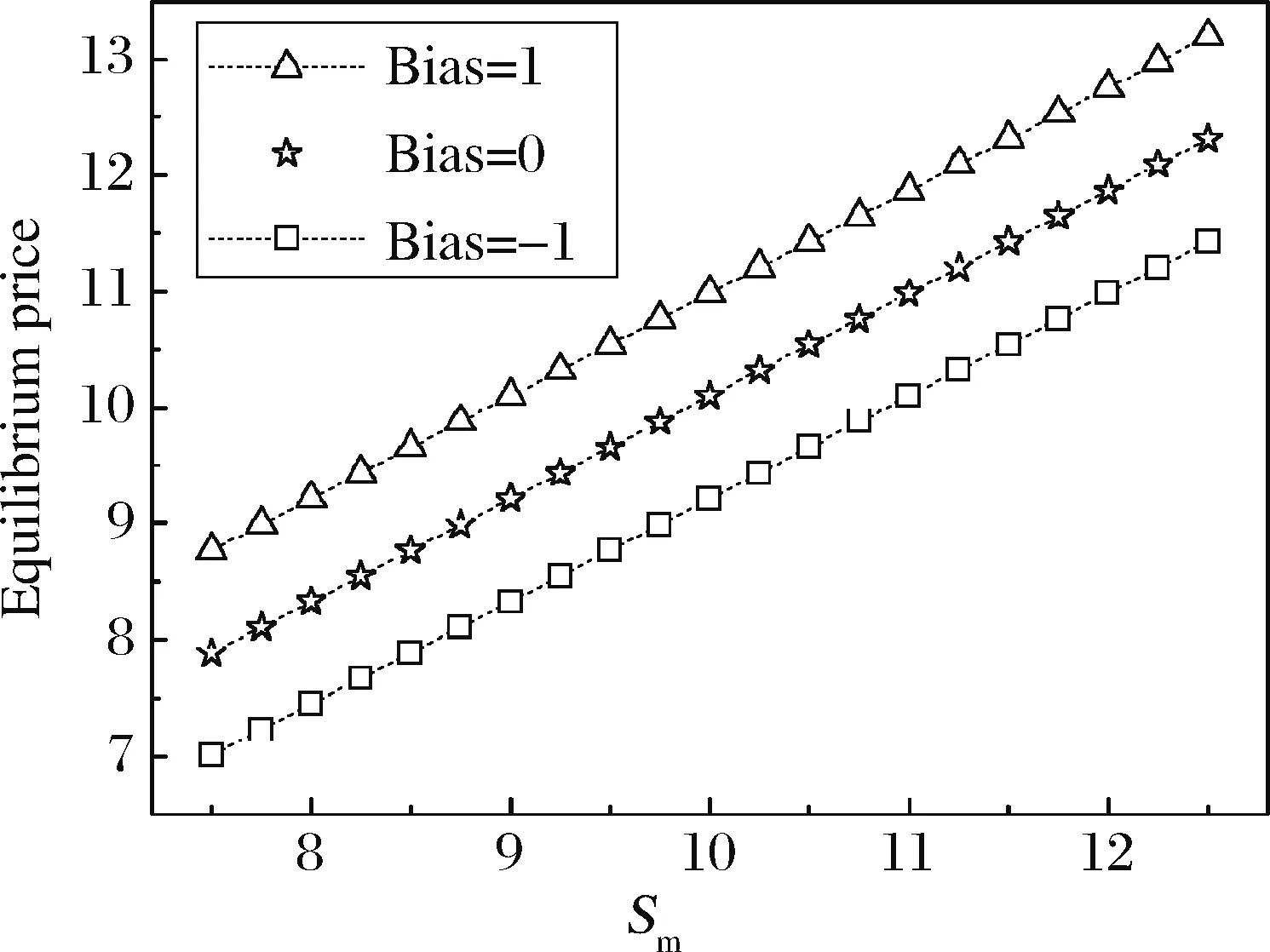
6.3 内幕交易者的最优操纵策略与交易者的损益
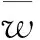
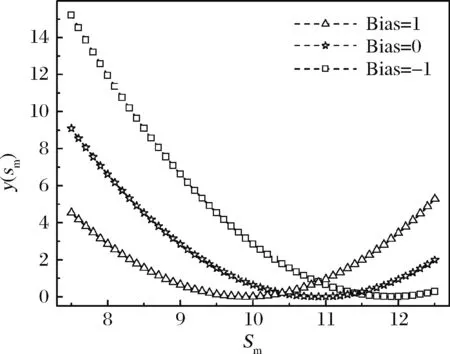
6.4 市场操纵甄别启示
7 结语