基于DWT 和FRFT 的数字图像水印算法

龚成清

（广东女子职业技术学院应用设计系，广州 511450）

0 引言

数字图像版权保护的问题是信息化时代研究的一个热点问题。数字水印是有效保护数字图像版权的方法。根据水印嵌入的区域不同，数字水印算法可以分为空间域算法和变换域算法[1]。变换域法因其鲁棒性好而得到广泛应用。常用的变换域法有离散小波变换（DWT）[2]、离散余弦变换（DCT）[3]、奇异值分解（SVD）[4]、分数阶傅里叶变换（FRFT）[5]等。

离散小波变换（DWT）是变换域法的典型代表，具有良好的特性。文献[6]将原图像进行多层小波分解，提出了一种基于DWT 变换域的数字水印方案，具有良好的鲁棒性，但水印的嵌入容量受到限制。文献[7]结合DWT 和SVD 的特点，利用DWT 变换构造水印后对系数矩阵进行SVD 变换，提出了一种基于DWT 和SVD 的数字水印算法。该算法具有良好的不可感知性和鲁棒性，但只适用于处理平稳的信号。分数阶傅里叶变换（FRFT）则可以用来处理非平稳的信号。相对传统的傅里叶变换，FRFT 具备运算速度快，高聚焦性等特性，可以有效提升水印算法的效率。文献[8]对整幅图像进行离散分数阶傅里叶变换，通过系数的修改提出了基于分数阶傅里叶变换的随随机序列水印算法，实现了水印的嵌入和提取，但图像容易失真。

本文利用DWT 和FRFT 的特性来提升水印的视觉性和鲁棒性。水印嵌入时，对载体图像进行DWT 变换，选择低频子带进行FRFT 变换后嵌入水印信息，同时生成两个伪随机序列（PN 系列）。利用FRFT 多角度变换的特性，在x 方向和y 方向均嵌入水印信息增强水印的鲁棒性。水印提取时，计算两个PN 系列与FRFT 的系数的相关性，并与阈值对比，确定水印的信息是0 还是1，从而提取出水印。

1 相关技术

1.1 DWT

离散小波变换是对基本小波的尺度和平移进行离散化。经过离散小波变换后图像会生成低频子带和高频子带。在图像处理中，常采用二进小波作为小波变换函数，第α层离散小波变换的函数如（1）、（2）所示。

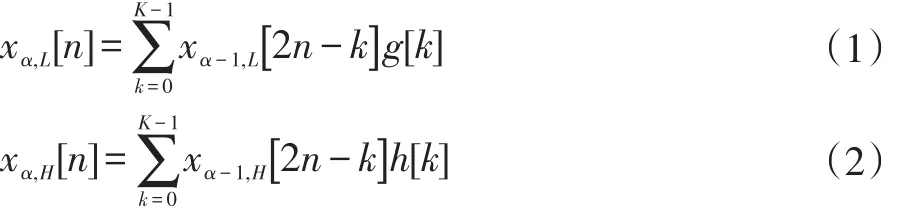
x[n]表示离散的输出信号，长度为N。g[n]是低通滤波器，可以将输入信号的高频部份滤掉而输出低频部份。h[n]是高通滤波器，与低通滤波器相反，滤掉低频部份而输出高频部分。

1.2 FRFT

FRFT 不但具有时域和频域双重特征，还具有旋转特性和角度连续性，是一种非常有效的信号分析工具，被广泛应用于数字水印领域[9]。运用分数阶傅立叶变换能选取信息最集中的角度去分析，在不同的分数阶得到的结果中选取幅值最大的那个结果，从而得到最优解。二维离散分数阶傅里叶变换形式如下：

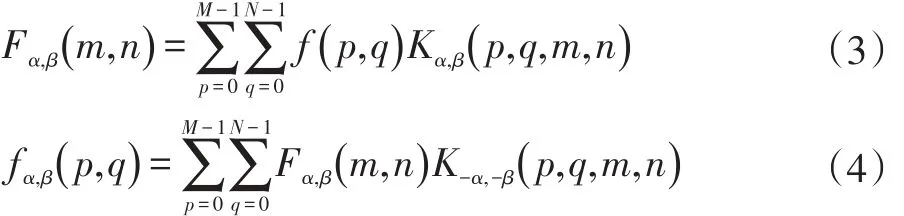
2 DWT-FRFT的水印算法

2.1 水印嵌入

水印的嵌入要兼顾视觉性和鲁棒性。利用DWT快速变换的特点，对载体图像进行2 级分解，选取低频子带进行水印嵌入，提升了水印嵌入的容量。对低频子带系数进行FRFT 变换，在x 和y 的角度方向都嵌入水印的信息，增强了水印的鲁棒性。具体算法如下：

（1）对载体图像进行DWT 变换；

（2）选取DWT 变换后的低频子带系数，进行二维FRFT 变换；

（3）定义起点F1 和系数的长度F2；

（4）读取水印图像，把水印图像的信息转化为向量；

（5）判段水印信息是否为1，如果是1，则起点和系数不作改变，F1=F1，F2=F2，跳转到第8 步。否则，跳转第6 步；

（6）使用密钥 key，生成两个随机序列 PN_h 和PN-v；

（7）更 新 F1 和 F2，F1= F1+K*PN_h，F2=F2+K*PN-v；

（8）判断是否所有水印信息已经完成变换，如果全部完成则进入下一步，否则跳转回到第5 步；

（9）把水印信息F1 和F2 嵌入到载体图像对应的位置，进行逆FRFT 变换，完成水印嵌入。

2.2 水印提取

水印提取是水印嵌入的逆过程。DWT-FRFT 的水印算法只需要使用水印嵌入时生成随机序列的密钥就可以实现水印的盲提取。提取过程中，使用公式（5）来计算提取信息的相关性，并与阈值进行比较，没有嵌入水印的阈值的期望为零，而嵌入水印的阈值的期望大于零。

具体算法如下：

（1）对含水印的图像进行DWT 变换；

（2）选取DWT 变换后的低频子带系数，进行二维FRFT 变换；

（3）定义起点F1 和系数的长度F2；

（4）使用密钥 key，生成两个随机序列 PN_h 和PN-v；

（5）对每个水印信息计算F1 和F2 与相应PN 序列的相关性；相关性大于阈值则水印信息是1，否则，水印信息是0；

（6）重复步骤4，直到所有的水印信息提取完成。

3 实验仿真

我们使用MATLAB 2018 对算法进行了实现，通过实验对算法的性能进行了验证。实验使用的操作系统是Windows 7，计算机配置为Intel Core i7 3.0G 的CPU，4G 的内存。为了评价水印图案提取的质量，使用归一化的相关系数NC 值来对提取出来的水印图案进行评价，NC 值计算公式如下：

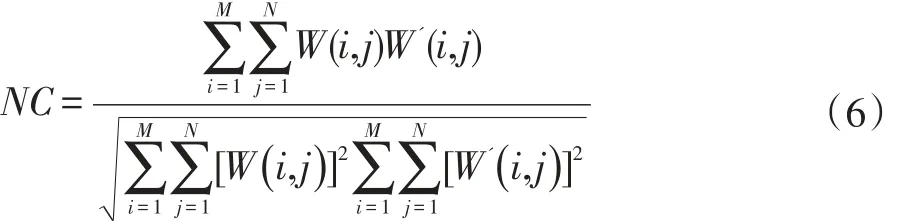
3.1 视觉性验证

为了验证嵌入水印后的视觉性效果，采用峰值信噪比PSNR 和来评价图像的视觉效果，PSNR 的计算公式表示如下：

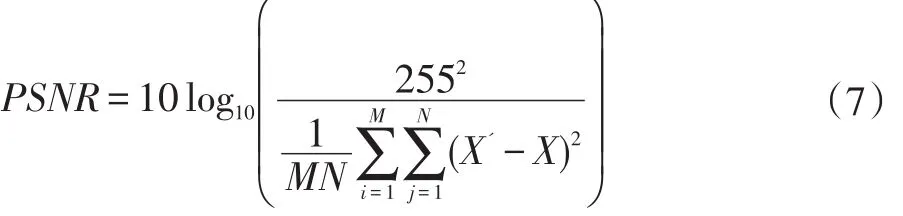
图1 水印的嵌入和提取

实验使用了512×512 的Lena 的彩色图像为载体图像，水印图像是32×32 的二值图像，使用DWT-FRFT算法对水印进行了嵌入和提取，实验结果如图1 所示。

嵌入水印后的图片具有良好的视觉性，与原始载体图片视觉效果一致，肉眼无法分辨差别。在没有受到攻击的情况下，实验对水印图像实现了盲提取，提取的水印图片与原始的水印图片相似度NC=1，能很好地还原出原始的水印图像。

3.2 水印容量验证

实验分别使用DWT-FRFT 的水印算法与文献[8]的算法把 64×64、128×128、256×256 的图 1（b）的水印图像嵌入到图 1（a）大小为 512×512 的 Lena 彩色图像中，两种算法的PSNR 计算结果如表1 所示。

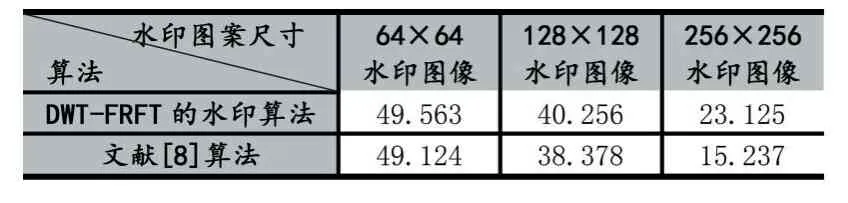
表1

实验结果表明，对于尺寸为128×128 以下的水印图案，两种算法均有较好的视觉效果。当水印的图像为256×256 大小时，两种算法进行水印嵌入后，PSNR有明显的下降，含水印的图像均出现了肉眼可见的杂点。DWT-FRFT 的水印算法由于选择的是能量集中的低频子带嵌入，视觉性影响较小，相对于文献[8]选择中频子带嵌入的算法，DWT-FRFT 的水印算法的视觉性更好，水印嵌入的容量更大。

3.3 鲁棒性验证

实验中，使用了DWT-FRFT 水印算法、文献[7]水印算法和文献[8]水印算法分别把图1（b）的水印图像嵌入到图1（a）的载体图像中并进行提取。为了验证不同算法的鲁棒性，实验过程对含水印的图像分别添加噪声、几何变换和压缩等操作进行了抗攻击的实验。水印提取后的NC 值如表2-表4 所示。

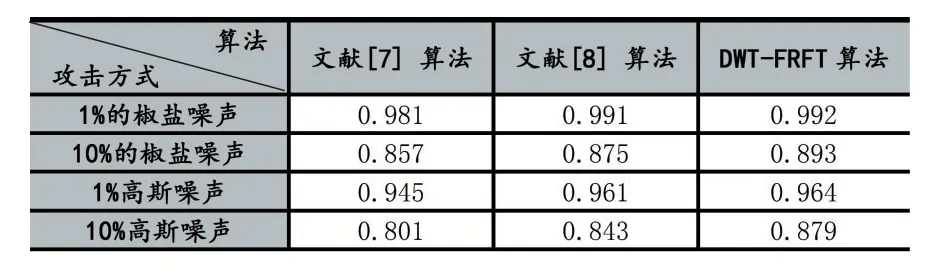
表2 不同算法抵抗噪声攻击的NC 值对比

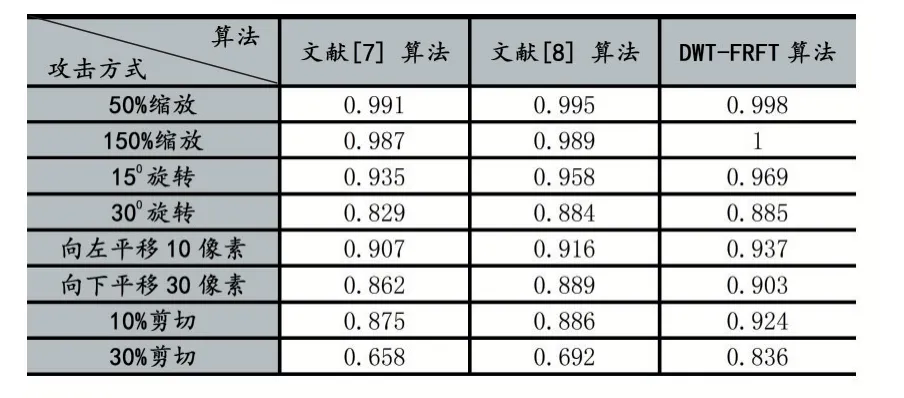
表3 不同算法抵抗几何攻击的NC 值对比

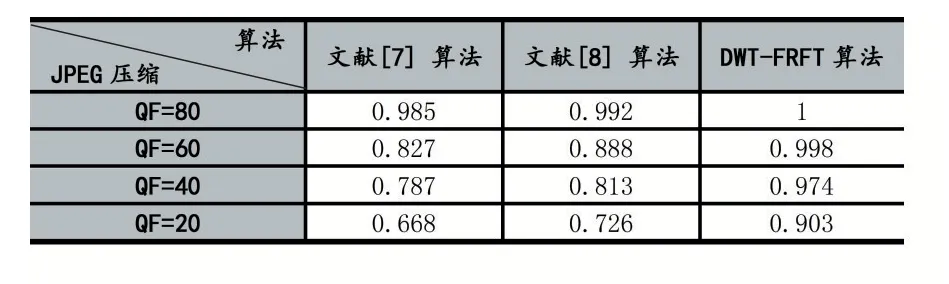
表4 不同算法抵抗JPEG 压缩攻击的NC 值对比

实验结果表明，DWT-FRFT 算法由于在x 方向和y 方向均嵌入了水印信息，具有充足的信息冗余，在抵抗攻击方面相对于文献[7]和文献[8]算法，具有更好的鲁棒性，尤其是在抵抗剪切和JPEG 压缩攻击方面，鲁棒性要远远优于对比的算法。

4 结语

为了更好地解决数字图像的版权保护问题，本文利用了DWT 变换速度快的特点，在不同尺度上对信号进行分解，选取能量集中的低频子带进行分数阶傅里叶变换后进行水印的嵌入和提取，解决了非平稳信号的处理问题。实验证明，本文提出的DWT-FRFT 算法水印算法不仅具有良好的视觉性和嵌入容量，对噪声、几何变换和压缩等常见的攻击等都具有很好的鲁棒性。