对函数表达的认知

韩 清

（广东外语外贸大学南国商学院信息科学技术学院，广东广州510545）

对函数表达式理解的偏差，会影响到结果的正确性。笔者在微积分教学中，遇到这样一道习题：找出函数

的间断点［1］。

大部分学生写为

上面的处理就有问题（得出f（x）连续的错误结果），但很多人不理解为什么会错。主要原因是他们普遍对函数的概念比较模糊，缺乏清晰的认识。像上面式（1），他们把函数化为函数x+1，觉得理所当然，问题就出在函数相等意味着什么。

本文就来讨论一下与此相关的函数表达问题。函数，是数学中最基本，但也不太容易说清楚的概念之一。所以，函数的定义（definition）在数学教学中三番五次一再重复出现。这在数学概念中很少见。大学生们在数学课程中学习函数这个概念，至少要在三个不同的阶段学三遍。

第1次是在初中，函数定义成变量［2］：如果在一个变化过程中有两个变量x和y，并且对于变量x的每一个值，变量y都有唯一的值与它对应，那么我们称y是x的函数（function），其中x是自变量。

到了高中，在建立了集合的概念之后，数学课第2次给出函数的定义［3］。这次，函数是对应关系：

设A，B是非空数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数（function），记作

y=f（x），x∈A，

其中，x叫做自变量，x的取值范围A叫做函数的定义域（domain）；与x的值相对应的y值叫做函数值，函数值的集合｛f（x）│x∈A｝叫做函数的值域（range）。

进了大学，数学课还会第3次定义函数［1］，函数既是变量（因变量），也表示对应规则：

设x和y是两个变量，若当变量x在非空数集D内任取一数值时，变量y依照某一规则f总有一个确定的数值与之对应，则称变量y为变量x的函数，记作y=f（x）。这里x称为自变量，y称为因变量或函数，集合D称为函数的定义域，相应地，y值的集合称为函数的值域，f是函数符号，表示y与x的对应规则。

综合来看，函数大致上有四种说法：

（1）对应关系；

（2）因变量 y；

1.税费同增长，组织收入规模进一步扩大。2017年7月代征后至12月，原梧州市、北海市地方税务局共征收入库社会保险费14.67亿元，其中原梧州市、北海市地方税务局分别征收入库9.97亿元、4.70亿元。2018年1～6月，两市税务部门代征社会保险费19.45亿元，其中原梧州市、北海市地方税务局分别征收入库10.62亿元、8.83亿元。收入规模进一步扩大，税务部门与地方发展联系更密切，为社会经济发展和民生保障发挥更大的作用。

（3）关系式：y=f（x）；

（4）含有自变量x的表达式f（x）。

因为对应关系难以确切描述，所以，数学上多用具体的关系式来表示两个变量的对应关系，也就是y=f（x），即第3种说法。这也是数学上函数最标准的表达方式。

若把第3种说法，也就是将关系式y=f（x）看成是两个式子相等（相同），则这个等式两边的两个式子，也就是y和f（x）就都可以简略地表示这个函数。这就是第2和第4种说法。

所以，在数学上，函数的表达基本上是3种：y，f，或者y=f（x）。

无论哪一种，一般都把函数看成是含有自变量x的表达式，也就是f（x）。

这就是说：函数相等，不仅要求对应关系一样（也就是函数式子的计算结果相同），而且定义域也要一样。

定义域不同的函数，肯定不相等。

另一方面，我们也可以从分式的角度来看。中学关于分式以及分式约分的定义如下［4］：

数学思维中相当一部分的推理、变换都不是等价的（必要而非充分）。这会导致出现很多似是而非的问题。这类问题非常普遍，限于篇幅，本文不深入讨论。具体到本文的例子，在分式化简时，约分往往不是恒等变换。这也是大多数学生认识的误区。类似的错误非常普遍，例如

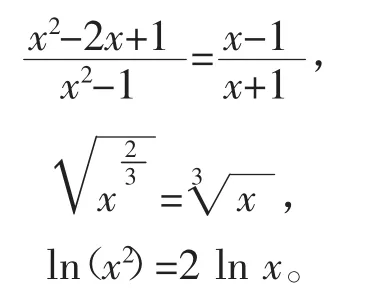
这样的认知，对于许多大学生来说，不太容易理解和接受，值得我们在教学中注意。