最优化设计在化工设备设计中的应用

刘育嘉(中石油吉林化工工程有限公司，吉林 吉林 132001)

0 引言

最优化设计在化工设备设计中的应用，可增强化工设备选用的科学行，对化工设备加以简化，省略部分繁杂的操作环节，控制问题的出现。同时也可达到资源优化，成本节省的目标，为化工企业经营贡献力量。

1 最优化方法及最优化设计

最优化方法，又称之为运筹学方法，得到公众的广泛认可。最优化方法，能够为决策者对某一个项目或某一项工作进行决策提供可靠的参考依据。同时，最优化方法以数学方法的应用作为表达形式。无论是各类生产经营活动，还是各种组织管理问题，都可以采用最优化方法实行统筹规划。

从某种角度来说，最优化方法的应用目的就是，在开展某一个项目或某一项工作的过程中，根据实际情况，对现有的人力、物力和资金进行合理分配，进而提高工作效率，创造最大化的效能或效益。

所谓最优化设计，也就是利用最优化方法，对生产过程中的各类影响因素予以综合性分析，之后利用计算机软件和多元化信息技术，获得符合实际情况的最佳设计方案。换言之，最优化设计也就是互联网时代、信息时代与大数据时代衍生的一种新型设计方式或设计手段。最优化设计往往借助数学函数关系式的形式予以表达。也就是说，最优化设计能够给出满足约束条件前提下的目标函数极值。

从微积分角度来说，约束条件至少要有两阶连续偏导数时，才能满足连续性的要求。由此可知，函数z=f(x)取极值的必要条件是dZ/d=0，此时，满足约束条件并使目标函数的一阶导数为零的x值则为所求的最优解。

2 最优化设计的应用

最优化设计的目的是做到各环节生产作业的最优化处理，将其应用到化工行业中，可做到产品质量的最优化，产品体积和重量的最优化、生产流程及资金成本的最优化，既增强化工企业的生产实力，又可增加企业经济效益。

在最优化设计中，会设定最优值，以此判断产品或流程的合理性与否。这里面的最优值与数学中的极值存在差异。数学中的极值是难以达到的极限值，而最优值则是通过多方对比分析获得的可以达到的最优效果。

在对最优化设计研究中，可将设计内容概括为：

其一，最优化设计需要一个最优值，设计人员要学会将传统的物理模型转化成数学模型，利用数学模型开展相关参数的计算，确定变量，为设计工作提供专项的约束条件。在这一阶段中，要处理好最优指标与设计变量间的函数关系，以加强计算的准确性。

其二，利用最优化探究方法对构建起的数学模型实行深入解析，找出最优值计算中存在的问题，参照现有理论依据，对这些问题加以解决，得出最优结果。目前最优化设计在很多领域中均得到了广泛应用，如航空航天、铁路、建筑、化工冶金、电气工程等，如图1所示为某工程不锈钢化工设备。

图1 不锈钢化工设备

3 最优化设计在化工设备设计中的应用

3.1 求导法

在化工设备设计中，如果发现其设计难度较低，可利用求导法来完成最优化设计要求，解决化工设备存在的问题，促进后续生产作业的顺利进行。例如，化工生产中需要的圆柱形薄壁化工储罐设备，在指导储罐各结构材料价格后，要求在设计中，确保化工储罐体积满足要求的同时，降低材料成本损耗。在这一过程中，可将化工储罐的体积设定为V，已有计算条件为：化工储罐盖子的材料每平方米价格为α，储罐罐身材料每平方米的价格为β，材料加工费用为γ，化工储罐的设计高度和直径分别以L和D表示，根据现有条件，计算储罐体积，并对比分析选出最省钱的设计方案。

储罐体积的函数计算公式为式(1)：

最终总金额以M表示，其是灌盖和罐体费用相加之和，计算中使用的函数公式为式(2)：

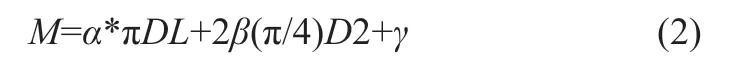
在这两个函数计算中，要求D、L参数大于或等于零。基本公式确定后，利用求导法不断推导和演化，得出最优化设计内容。后续的推导演化过程为：结合上述V=(π/4)D2L公式利用求导法，可得出L的表达式(3)：

之后将该数值带入到式(2)，得出式(4)：

该公式得出后，将D的一阶导数设置在0，得出式(5)：

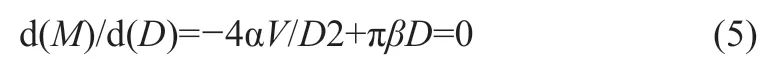
经过计算后得出式(6)：

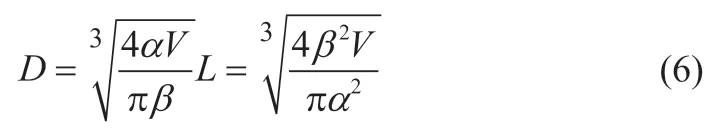
D、L数值可直接带入到公式(2)中，得出最优化设计方案。

3.2 拉格朗日乘子法

如果在最优化设计中，存在的约束条件复杂性较强，且存在变量，难以做到科学管控时，可直接使用拉格朗日乘子法求解，得出最优化设计方案。该方法应用的具体步骤流程为：

将加入到目标函数里的每一个约束方程都分别乘以λ1，λ2，λ3，…，λm，设最终费用为L，N=M+λ1g1(x1)+λ2g2(x2)+…+λmgm(xm)。在该公式中，L代表拉格朗日算子，公式中多次出现的λ则是拉格朗日的乘子。最终N值的获取可对变量x和乘子λ进行控制，将导数设置为0，之后利用公式间的关联求解，得出最优化设计。

同样以上文提到的储罐最优化设计为例，不过这里不是体积的求解，而是壁厚的计算。储罐体积仍以V表示，材料强度应力以[σ]代表，内部液体密度为ρ，储罐的尺寸以D、T、L代表，计算壁厚，得出最优化设计方案。

先计算用量体积：M=πDLT+21/4πD2T=πDLT+1/2πD2T。数学模型中，提出的约束条件为：容积V=1/4πD2T；强度[σ]=ρLD/2T。

利用这几个公式可得出储罐的最优化数学表法式：M=πDLT+1/2πD2T，S.T.:1/4πD2L-V=0，ρLD/2T-[σ]=0。

然后将拉格朗日乘子λ引入其中，对约束条件加以计算，N=πDLT+1/2πD2T+λ1(1/4πD2L-V)+λ2(ρLD/2T-[σ])。

之后将N对D,T,L这三个设计变量和λ1、λ2这两个拉格朗日乘子分别进行求导，使其等于0，最终得出五个导数公式，利用五个导数公式关联求解的结果得出最优方案中D、L、T的参数值，再利用这三个参数，确定最终的最优化设计方案。

3.3 图解法

对于不符合上述情况的化工设备设计，为达到最优化设计要求，一般会采用图解法的方式求解。尤其是在单数设计中，其在最优化设计中是最难以求解的一个环节，无法使用数学模型操作，这时就需要利用图解法的参与。图解法在使用中，存在的变量不得超过两个，如果超过，能够将变量转化成两个，也可使用图解法。

以受内压圆柱形薄壁容器的最优化设计为例，对图解法求解的流程加以分析。一个圆柱薄壁型容器，壁厚在3mm以内，长度固定值2m，以L表示，容器体积在4m3以上，容器承受的内压可达到2.5MN/m2，容易内压以P表示，材料强度应力[σ]，内部液体密度ρ。

本次设计需要对容器的重量加以计算，得出容器直径和容器具体壁厚值，以这两个数值确定最优化设计方案。

在求解中容器还存在以下约束要求：

(1)强度要求

容器内薄壁应力分别为：σ1=PD/2T，σ2=PD/4T，σ3=0，强度的约束条件利用第三强度理论计算得出：2.5D/2T-120≤0.2。

(2)其他要求

由于该容器属于薄壁类型，所以容器的壁厚T要求小于或等于直径的1/20；容器体系在4m3以上，也就是说1/4πD2T应等于或大于4，这样计算得出容积体积等于或大于1600；壁厚需等于或大于3mm。

结合这上述约束条件，计算容器重量，M=ρπDTL=0.156πDT。根据上述条件，推导得出Min:M=0.156πDT, S.T.：2.5D/2T-120≤0，T-D/20≤0，D≥1600，T≥3，之后利用图解法推导出容器的最优化尺寸，即D=1600mm，T=16.7mm，该容器重量的最优效果是13kN。

4 结语

综上，在化工设备设计中，最优化设计在优化设计水平，提高设备使用率，节省资金成本上有着显著优势，不过由于最优化设计的方式方法较多，设计人员需根据实际情况选择使用方法，最后得出最优解，判断方案的可行性，达到化工设备生产要求，保证化工产品质量。