基于人工鱼群算法的声矢量传感器阵列的最大似然DOA估计

王 鹏，贺雪芳，张明星，白艳萍

(中北大学 理学院，太原 030051)

波达方向(DOA)估计作为阵列信号处理的一部分，在通信、雷达和声呐等领域有着大范围的应用[1-2]。在过去几十年对DOA估计的研究发展中，出现了很多经典的估计技术，其中包括最大似然法(ML)、多重信号分类(MUSIC)、旋转不变子空间(ESPRIT)等方法[3-6]。其中ML就是一种比较独特且估计性能出众的算法，它将含参的联合概率密度函数作为观测信号的似然函数，之后通过最大化求解的方式来进行DOA估计，这使得它在面对低信噪比，小快拍数据等不利情况下，依旧有着不错的估计效果[7]。但该算法在求解非线性似然函数最优解时，自身的多维搜索会导致庞大的运算量，这严重影响了它的工作效率，限制了它的工程实用性和适用性。

为了解决ML多维受限的问题，已有学者提出了很多行之有效的方法，比如轮换投影法(AP)[8]，迭代二次型极大似然(IQML)等[9]；除此之外，还包括近年来提出的利用智能优化算法的思想来解决，比如遗传算法(GA)，粒子群算法(PSO)和差分进化(DE)法等[10-16]，这样就可以利用它们通用性强、全局优化性能高以及适合并行处理的优势，来完成搜寻目标方向角度的任务，而且在实验中都取得了不错的估计效果。

本文将人工鱼群算法(AFSA)应用于其中并优化似然函数，利用鱼群优化算法的高效性和自身所具有的强自适应性，能够避免像GA和PSO等算法一样出现早熟和收敛慢的问题；与此同时，为了进一步提高估计速度和精度，还对标准人工鱼群算法的视野(visual)和步长(step)进行了动态调整，实验对比结果证实了改进算法的有效性和实时性，并在一定程度上拓展了算法的实际应用性[17-20]。

1 矢量水听器的阵列信号模型和最大似然DOA估计

1.1 矢量水听器的阵列信号模型

考虑L个远场非相干窄带信号源从不同的角度θi(1,2,…,L)入射到阵元数为M的均匀线阵上，且各阵元之间相互独立。阵列的接收信号为

X(t)=Aq(θ)S(t)+N(t) .

(1)

式中：X(t)为3M×1维的阵列输出矢量，S(t)为L×1维的信号源矢量，N(t)为3M×1维的零均值高斯白噪声矢量，且噪声与信号相互独立。而Aq(θ)为3M×L维的矢量水听器阵的信号方向矩阵，具体结构为

Aq(θ)=[aq(θ1),aq(θ2),…,aq(θL)]=[ap(θ1)⊗
u1,ap(θ2)⊗u2,…,ap(θL)⊗uL] .

(2)

式中：aq(θi),i=1,2,…,L为矢量水听器阵的方向矢量，阵元对第i个信号的声压响应系数记为ap(θi)=[1,ejφi,…,e-j(M-1)φi]T，其中的φi=2πdsin(θi)/λ，λ为信号最大频率的相关波长，d为阵元间距。ui=[1,cos(θi),sin(θi)]T为第i个信号的方向矢量。符号⊗为克罗内克积。

基于上述条件，阵列接收信号的协方差矩阵为

(3)

式中：Rs是信号的协方差矩阵；σ2是阵列接收噪声的功率；I是单位矩阵，(·)H则表示该矩阵的复共轭转置。在实际运算中，考虑到接收数据长度是有限的，所以阵列协方差矩阵为

(4)

式中：K为快拍数。

1.2 最大似然DOA估计

在满足1.1小节的条件下，假设信源数已知或通过其他方式估计已获得，则由确定性最大似然(DML)，可得到样本数据K次快拍的联合概率密度函数为

(5)

式中：det{g}为该矩阵的行列式。将未知参量σ2和S的确定性最大似然估计代换进式的负对数函数中，通过该方法可得到关于参量θ的最大似然估计为：

(6)

式中：tr(g)为该矩阵的迹，PAq=Aq(θ)(AqH(θ)Aq(θ))-1AqH(θ)为正交投影矩阵。

2 最大似然DOA估计的优化

2.1 人工鱼群算法

人工鱼群算法是李晓磊等[17]在鱼群行为研究的基础上提出的一种群体智能优化算法。该算法结构简单，仅以目标函数值为准则，引导人工鱼向着食物充足的方向快速游动。于此同时，人工鱼个体通过行为的变化调整状态，以减少不利环境和部分因素变更造成的影响，促使个体不断向全局极值逼近，避免出现在局部极值附近停留的状况。总之，该算法具有鲁棒性强、收敛速度快、对初值要求不高等优点，很适合用来优化1.2小节提到的最大似然估计函数并找到该函数的全局极大值。

人工鱼群算法是一个搜寻水域里最高食物浓度位置的过程，这片水域就是解决问题所需的解空间，也是限制鱼群活动的最大范围。食物浓度值和位置作为两个重要的观测值，其相关数据都蕴含在人工鱼中，这样不但方便了人工鱼在迭代过程中实时的更新自己，还有助于人工鱼的行为选择。在搜寻过程中，人工鱼依靠自己的视野和步长来探索环境和随机游动，在聚群过程中，人工鱼根据彼此距离来统计当前视野内的个体数量与位置，并计算此时中心位置的浓度值与拥挤度，若中心位置浓度更高且不拥挤时，就朝着中心位置的方向适当的移动，完成聚群行为，否则的话执行觅食行为。在追尾过程中，同样要统计视野内的个体数量和位置，寻找出浓度最高的伙伴，并计算该伙伴的拥挤度，若该伙伴的周围不拥挤时，就朝着该伙伴的方向适当的移动，完成追尾行为，否则的话执行觅食行为。在这两种行为中，拥挤度的计算是必不可少的，它能避免人工鱼在某一范围内过度拥挤而陷入局部最优，保证了算法的稳定性和全局性。而在觅食过程中，参数try的作用至关重要，它控制着人工鱼搜索新位置的次数，若新位置的浓度更高，则向新位置靠近，否则的话就舍弃。如果在规定次数内仍然找不到，就开始进行随机游动。所以说它的大小反映着觅食能力的强弱，选取合适的该参数能够有效提高算法的收敛性能。

在算法迭代中，通过改变视野和步长的取值方式，能够提高算法的收敛速度，或者适当扩大鱼群规模，以此来增强算法克服局部最优解的能力。人工鱼群算法的主要步骤如下：

1) 设置鱼群的初始位置和其他算法参数；

2) 选用食物浓度函数并将其作为评判个体位置优劣的唯一标准，并且计算所有个体的食物浓度，将最优值和其对应的个体位置记录在数据表中；

3) 分析人工鱼个体视野领域内的环境条件，根据结果来选择聚群、追尾或觅食行为；

4) 执行所选的行为活动，随即更新自己的位置与食物浓度，最终构成新的鱼群；

5) 统计所有个体的食物浓度，如果优于数据表的记录，则更新为该浓度值和其所对应的个体位置；

6) 若达到迭代次数上限，算法终止，否则转至步骤3).

2.2 基于IAFSA的最大似然DOA估计的优化

将人工鱼群算法应用于最大似然的DOA估计中。把式(6)的似然函数看做优化问题的目标函数，用该函数来计算食物浓度值，且食物浓度值所对应的解向量，就是所有待估计方向角的一个可行解。而关于最大化目标函数的问题，其实就等价于在水域中搜寻出最高的食物浓度值，最终找到对应的全局最优解。

假设鱼群规模为P，搜索维数等于信源数L，即每一条人工鱼的状态位置Xi=[xi1,xi2,…,xiL],(i=1,2,…,P)都是L维的。拥挤度因子δ为0.6，参数try不固定，会根据实验做出适当改变。对视野(V)和步长(S)按照式(7)进行非线性动态调整，使得算法前期以全局搜索为主，后期锁定到最优解的大致位置时，则以局部精细搜索为主。

(7)

式中：Vmin=5，Vmax=20,Smin=3,Smax=5,常数c=50，n和nmax分别为迭代次数与最大迭代次数。

搜索范围为[Xmin,Xmax]，其中Xmin=0 °和Xmax=180 °是人工鱼活动的上下限。按照式(8)对鱼群位置进行初始化。

Xi=Xmin+rand(0,1)(Xmax-Xmin) .

(8)

食物浓度函数定义为下式：

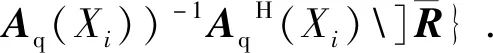
(9)

在每次迭代中，每条人工鱼都要在3种行为方式中选择1种。当人工鱼选择觅食时，该个体在视野领域中按照式(10)所示随机游动，通过感知食物浓度的高低来逐次寻找可以自己前进的方向，并在这个方向上按照式(11)所示游动

(10)

(11)

式中：rand()为介于(0,1)的随机数，‖Xj-Xi‖代表个体间的距离，其中的Xj和Xnext均表示下一步的位置，只是形式表达需要而已。而执行聚群所依靠的拥挤度由式(12)给出

(12)

式中：nf为视野内伙伴数目，ρfood,c是中心位置的食物浓度，ρfood,i是当前位置的食物浓度。将该拥挤度与δ做比较，并以此判断是否执行行为。同时追尾中拥挤度的计算与式(12)一样，只需用最优伙伴位置Xu的ρfood,u替换ρfood,c即可。

参数的选择与调整，都是为了提高人工鱼克服局部最优解的能力，尽可能的向着全局最优的方向游动。在合适的参数条件下，通过几次迭代，算法就可以准确地找到最高食物浓度以及对应的全局最优解，即需要的DOA估计角度。

3 仿真实验及性能分析

所有实验中均选择以上提到的GA，PSO和DE这3种智能优化算法，且采用六元矢量水听器阵列，均匀线阵和300个数据快拍。

3.1 收敛性能

收敛性能能够很好地反映算法的估计效率。为了得到准确的实验结果，在平均100次的实验中获得了似然函数最大值随迭代次数增加的曲线图。仿真实验采用两个信号源，方向为θ=[30° 60°].所有算法的总体数量设为30，迭代次数为100，并且算法的其他参数被适当地调整。

图1显示了IAFSA，GA，PSO和DE这4种算法在信噪比SNR为0 dB和-15 dB时的收敛性能。从迭代曲线中发现，IAFSA算法在两个实验中均表现优异，且相较于其他3种算法而言，IAFSA算法不仅收敛速度快，还能准确找到似然函数的最大值。另外，在SNR为-15 dB时，PSO算法已经失去了效果，只能找到一个局部最优值，这说明PSO算法在低信噪比时的性能远不如其他3种算法。

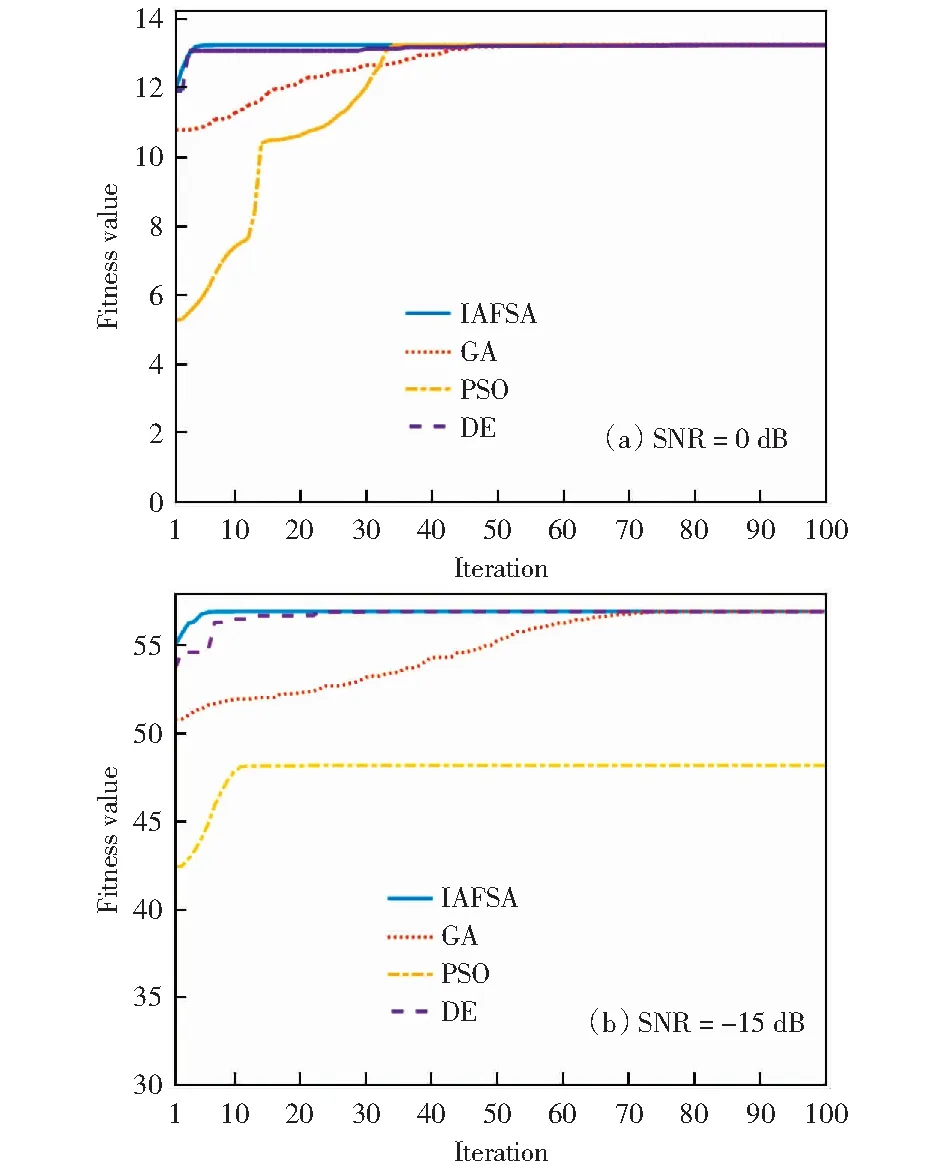
图1 两信源下似然函数的最大化曲线Fig.1 Maximization curve of likelihood function under two sources

为进一步检验IAFSA算法的收敛效果。图2显示了在信噪比为0 dB时，信源数增加情况下的变化曲线图。四信源时的方向为θ=[30° 60° 80° 150°]，而三信源时则依次取前3个。在实验中，由于部分算法的需要，将迭代次数增加到了200次，以保证实验结果的完整性。其余条件则与上述实验保持一致。

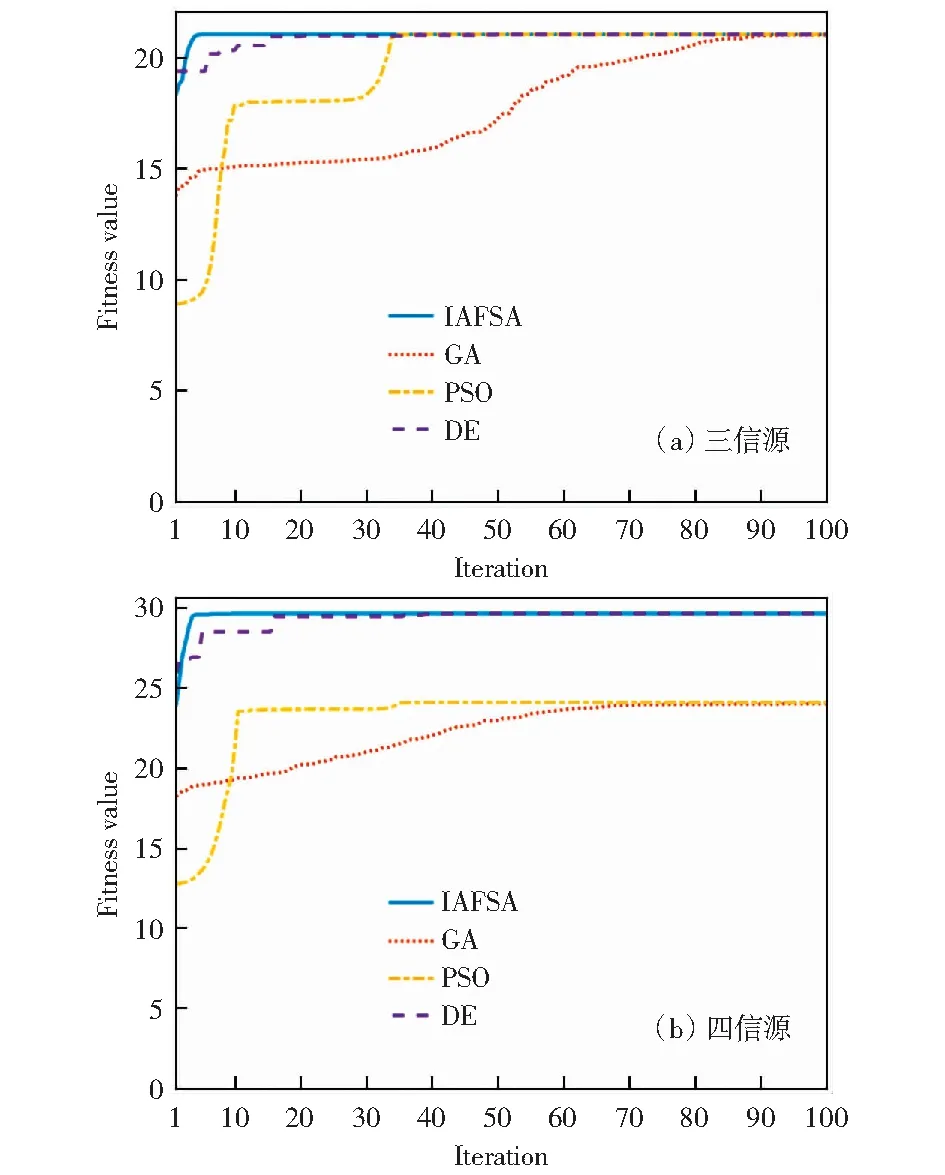
图2 信噪比为0 dB时似然函数的最大化曲线Fig.2 Maximization curve of likelihood function with signal-to-noise ratio of 0 dB

从图2中看出，信源数的增加对IAFSA算法的影响并不大，DE算法的状况比较良好，但是GA和PSO的情况就不容乐观了，在实验中面临的状况要么是迭代次数的大幅度上升，要么就是失效，即只能收敛到局部最优解，同时这些问题也影响着算法的性能与计算量。

3.2 误差统计

为比较信噪比条件下4种算法的DOA估计性能，进行了100次蒙特卡罗实验，并以均方根误差(RMSE)作为判断标准，以此来验证各算法的误差统计特性。均方根误差(ERMS)计算公式为：

(13)

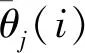
实验中设置信噪比(SNR)从-20 dB到20 dB，间隔为2 dB，其余实验条件与3.1节保持一致。图3分别表示了信源数为2、3和4时，DOA估计的均方根误差值ERMS随信噪比变化的曲线图。

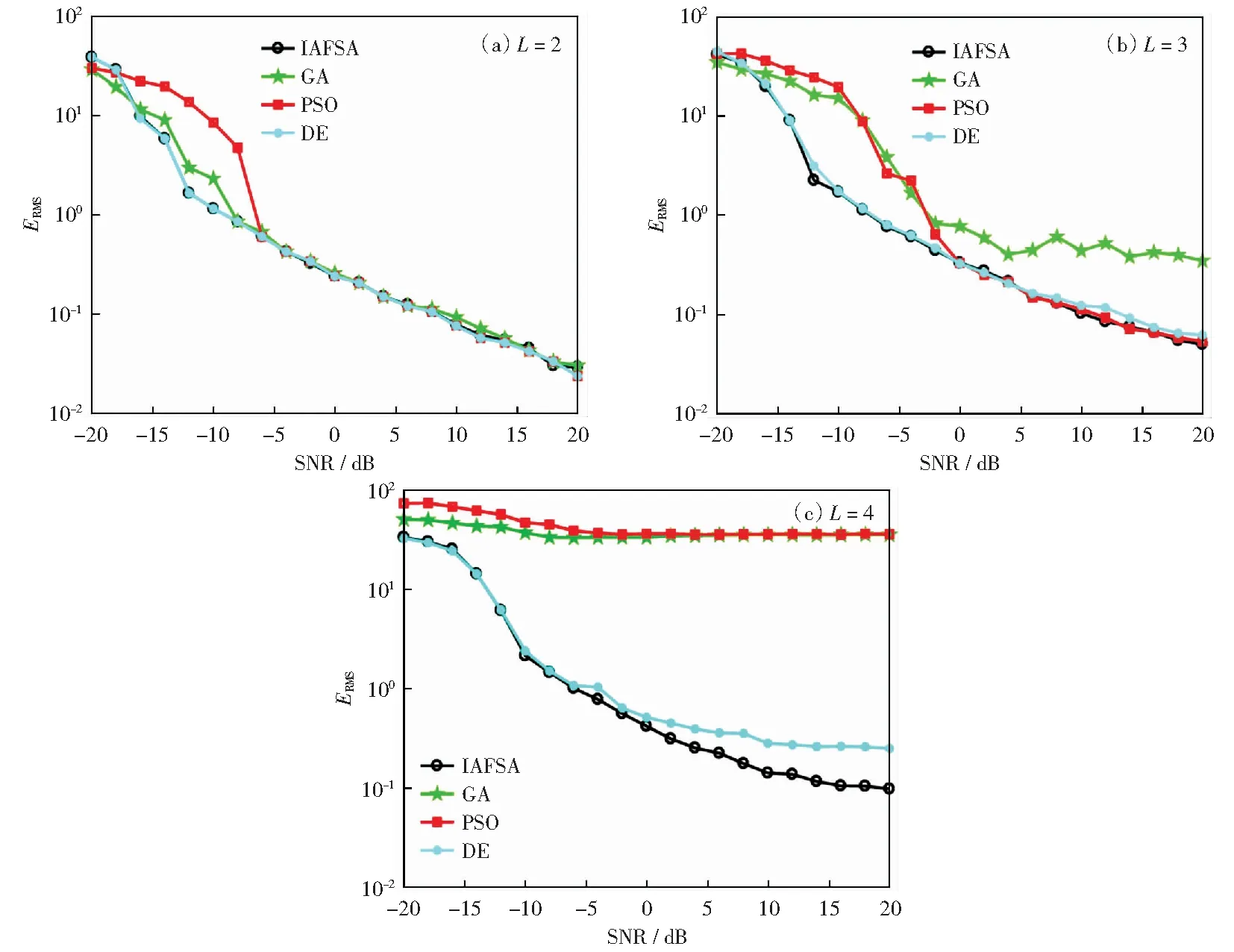
图3 DOA估计的均方根误差值ERMS随信噪比的变化曲线Fig.3 Curve of ERMS against SNR estimated by DOA

从图像上发现，随着信源数增加，4种算法的RMSE曲线发生了不同幅度的上升。其中GA和PSO的变化尤为明显，在L=2,3时，它们与IAFSA和DE曲线的差距还不大，PSO算法甚至在高信噪比时能够非常接近于这两条曲线，而GA算法则相对较弱一些。直到L=4时，这两种算法已经远远偏离了IAFSA和DE，这说明它们只能收敛到某个局部最优解。至于IAFSA和DE，这两种算法从始至终都很稳定，RMSE曲线不但很接近，而且变化幅度很小，在估计性能上明显优于其他两种算法。

此外，低信噪比下的IAFSA和DE的整体曲线也要低于GA和PSO，并且这种情况在L=2,3,4时都存在。随着信源数量和SNR的同时增加，GA和PSO的RMSE曲线开始逐渐偏离，一直到L=4时，曲线始终高居不下，这说明算法的估计性能已经完全失效，而此时IAFSA和DE的估计效果依旧比较良好，并且IAFSA的整体情况略好于DE，这也说明了改进方式的有效性和估计优势。

3.3 运算量分析

利用智能优化算法解决最大似然DOA估计的问题时，种群个数的选取非常重要，数量过少会加大搜索的难度，数量过多则会增加算法的运算量。在不影响算法估计精度的前提下，合理的选取种群数量，是有助于提高算法速度与效率的。

考虑信噪比为0 dB时不同信源数传播到阵列的情况。图4分别表示了信源数为2、3和4时，DOA估计的均方根误差值ERMS随Population size变化的曲线图。

从图4可以看出，在L=2时，所有算法在种群数量超过30以后都能达到一个非常接近的误差值，在L=3时，IAFSA和DE的情况变化不大，而其余两种算法则就需要更多的种群数量才能够达到与它们一样的估计效果，但是从整体上看，信号源数的增加也导致所有算法的误差值都有所上升。直到L=4时，IAFSA和DE的误差值依旧在上升，但是幅度不明显，即使是这样，这两种算法还是需要增加种群数量到30，甚至是40之后才能达到一个比较稳定的误差值。并且GA与PSO的曲线已经完全和它们分离开来，超出了可以接受的估计范围，失去了本身估计的作用。从始至终，IAFSA和DE的曲线都很接近，但IAFSA还是略好一些，而且使用的种群数量也是最小的，这有效地降低了算法的计算量。

图4 DOA估计的均方根误差值ERMS随Population size的变化曲线 Fig.4 Curve of ERMS against Population size estimated by DOA

4 结论

本文基于寻找极大值的思想，提出了用IAFSA算法来优化ML的似然函数，并以此为目标函数进行快速搜索求解。仿真结果表明，所提算法相较于GA，PSO和DE这些算法而言，具有更快的收敛速度和更好的收敛效果；与此同时，分析讨论了所有算法的误差统计特性和运算量影响，发现相较于其他三种算法而言，IAFSA算法拥有更小且更加稳定的估计精度，这说明在一定程度上该算法进行DOA估计时是更具有优势的。另外，实验结果的表现也说明所提改进方法的有效性，它不仅保证了估计精度不受影响，同时还能进一步减少迭代次数，同等实验条件下大大减少了算法的计算量。因此，基于IAFSA算法的最大似然DOA估计是一种非常有效的DOA估计方式，有利于实际应用的实现和拓展。