“三环四步法”深挖教材例题——以“菱形的性质”例题教学为例

弥勒市西山民族中学 史计春

在整个初中数学教学过程中，例题发挥着重要的作用.它们不但是资深的教育专家精挑细选、仔细推敲的产物，也是对课本知识概念的强化与延伸，更是体现数学思想与方法的重要载体.然而，在现实的例题教学中，却存在一些问题：少数教师对课本上的某些例题置之不理；一部分教师对例题只是就题讲题，没有进行深度挖掘、拓展；一部分教师虽然讲了例题，也对例题进行了一些拓展，但是学生遇到类似的题目还是不会做.由于对例题学习得不够深入，一部分学生只会做教师讲过的例题的原题，对于由例题衍生出来的新题却一窍不通；一部分学生遇到与例题类似的题目，教师一讲就会，但是自己一做就错，缺乏独立解决问题的能力；更有甚者，把课本上原模原样的例题单独拿出来测试，仍然不会做.在例题教学中，面对这些问题，笔者尝试采用“三环四步法”（三环节四步骤方法）来解决.这个方法能充分发挥例题的导向性和示范性，使例题的功能和价值最大化，让学生通过对一道例题的深度剖析，会解与例题相关的一类问题.

第一环节：作好例题教学前的知识铺垫与储备

在“讲菱形的性质”一课的例题之前，学生已经通过自己的“探索─猜想─验证”，学到了菱形的边与对角线的特殊性质：①菱形的四条边都相等；②菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.为了让学生更深入地理解这两个性质，为后面例题的学习作好铺垫，我用3 分钟左右的时间让学生做了以下4 个问题的知识抢答，以便检测学生对所学知识的巩固与理解情况.

1.（菱形特殊性质的理解）仅菱形具有而平行四边形不具有的性质是（）

A.对边相等 B.四条边相等

C.对边平行 D.对角线互相平分

2.（菱形的性质中，角的应用）在菱形ABCD 中，两条对角线的交点为O.若∠BAD=80°，则∠BAO=__________，依据是________________.

3.（菱形性质中，边、对角线的应用），在菱形ABCD中，两条对角线的交点为O.AC=8，BD=6，则AO=_____，BO=_____，依据是_____________________；这个菱形的周长为___________.

4.（菱形的性质中，边、角、对角线的综合运用）在菱形ABCD 中，两条对角线的交点为O.若∠BAD=60°，BO=2，则BD=________，AB=________，周长为_________，AO=__________，AC=_____________.

设计意图：有些学生在学习数学时，缺乏学以致用的能力，他们面对的问题是学知识点容易，用知识点难，特别是不会综合运用数学知识.教师可以把这些综合性较强的数学题，逐级分解成学生容易解决的简单问题，为学生解决难题铺好台阶，方便学生更好地摘到数学树上的果子.所以，在讲解例题之前，要加强基础知识的简单应用训练.我设计的题目侧重于应用基础知识，由浅入深、由单一到综合，学生容易得出答案，既让所有学生都巩固了“菱形的性质”这部分知识，又为后面例题的学习作了知识应用上的铺垫.这样做，不但让所有的学生在基础知识和基本技能上得到了加强与巩固，也让学生在知识抢答中不断增强学习数学的自信.

第二环节：重视并深度开发课本上的例题，充分发挥例题的导向性和示范性

所谓重视课本上的例题，就是多角度去挖掘例题的解法或拓展例题，把例题讲活、讲透.数学教育家弗赖登塔尔说得好：“学习数学唯一正确的方法就是‘再创造’，也就是由学生本人把要学的东西去发现和创造出来；教师的主要任务是引导和帮助学生去进行这种再创造工作，而不是把现存的知识灌输给学生.”这就要求教师在对待教材中的例题时，一方面，要引导学生自己去找出解题的思路、方法和技巧；另一方面，由于初中数学教材中的例题往往是比较经典、具有一定代表性的，因此一定要充分尊重教材中的例题，避免随意更换，甚至不讲例题.在深入了解教材例题的设计意图后，立足于教材，挖掘例题背后蕴含的知识、方法、思想，并从课本例题的命题背景、题设与结论、解题方法与思路、拓展与衍生等方面去深度开发，从而创造性地使用教材和处理教材.这个环节是数学教学的中心环节，是一堂课的灵魂，做好了这一环节，就可以让整个数学例题教学血肉丰满.教师可以从以下四个步骤入手.

第1步：清楚而透彻地分析例题

在例题教学中，教师要重点教会学生分析问题的思路和方法，让学生通过一道题，学会用演绎和归纳的方法去解决一类题.在例题教学中，教师应引导学生充分而全面地找到题目的已知条件和结论，通过师生、生生积极互动，把题目分析得清楚、透彻，将例题积极应用在学生对知识点的巩固运用上，尽量拓展学生思维，尝试着一题多解，让学生明白怎样分析题目、运用知识，并明白为何这样解，最后规范答题过程.下面以人教版八年级《数学》下册“菱形的性质”一课的例2 为例，谈一下我深挖课本例题的方法.

课本例题：如图1，菱形花坛ABCD的边长为20 m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长（结果保留小数点后两位）和花坛的面积（结果保留小数点后一位）.

师生互动分析：教师先引导学生找到题目的已知条件与结论（是什么），再找出已知条件与结论的关系（什么关系），最后分析通过哪些办法可以由已知条件得出结论（怎么做）.解题方法：可以采用由条件得出结论的正向思路分析法，也可以用综合分析法或由结论推出条件成立的逆向思路分析法（反证法）.具体分析过程如下：

正向思路分析法：菱形花坛ABCD 的边长为20 m，根据菱形的四条边都相等，得出AB=BC=CD=AD=20 m，由菱形的对角线互相垂直，得出BD⊥AC，又由BD⊥AC 可知△ABO是Rt△.

图1

方法一：由∠ABC=60°，根据菱形的对角线平分每一组对角可知∠ABO=30°，又因为△ABO 是Rt△，由直角三角形中，30°所对的直角边是斜边的一半，可知AO=10 m，进而得出菱形的一条对角线AC=20 m.

方法二：由∠ABC=60°，AB=BC，根据有一个角是60°的等腰三角形是等边三角形，可知△ABC 是等边三角形，再由等边三角形的三条边都相等，同样可以得到菱形的一条对角线AC=20 m.

问题是求两条小路的长，可以把实际问题转化为菱形这个数学模型，进而转化为求菱形的对角线的长.分析题目后，不难发现，已经求出一条对角线AC=20 m，而求另一条对角线BD 的长，可以用逆向思路分析法：先求BO，由△ABO 是Rt△，根据勾股定理求出BO；要求菱形面积，可将其转化为求四个小直角三角形面积的和.

第2步：规范学生的表述过程

师生互动分析题目后，教师要查漏补缺，规范解答过程，因为初中数学的答题过程，要按一定的格式进行.解题过程表达要清晰，论证依据要充分，结论要明确.为避免学生写出的解题过程思路不清、逻辑混乱、漏洞百出、没有突出重点等情况发生，教师规范解答过程就非常重要.规范解答过程，一方面可以让学生把握考试时的得分点，保证思路能清晰地表达；另一方面，不但能培养学生熟练驾驭数学符号的能力，也能培养学生良好的逻辑表达能力，形成严密的逻辑思维.当然，还要规范学生的解答过程.在规范解答过程时，对于基础较弱的学生，教师可以直接通过板书示范来规范；如果课堂时间紧迫，也可以播放课件展示解答过程来规范.然而，最好的方法是先让学生自己试着书写过程，教师再指出其中的问题.这样可以加深学生对知识的理解，但缺点是浪费时间.在教学中，教师可以根据实际情况，灵活地选用规范学生解题过程的方法.

规范的解题过程：

解法1：

设计意图：解法1 是课本上的解法，在算对角线的长度之前，还需要让学生复习一下保留小数点位数的知识.解法2 是教师引导学生得出的另一种解法.在例题教学中，教师要营造一个宽松的课堂氛围，采用讲授、讨论、探究等方式，引导学生不断地去发现新思路、寻找新解法，不但拓展了学生的思维，也培养了学生的创新思维能力，从而促进学生学习能力和数学素养的有效提高.适当进行一题多解训练，可以激发学生发现与创造的强烈欲望，加深学生对所学知识的深刻理解，锻炼学生思维的广阔性、灵活性和创造性，从而培养学生的思维品质，发展创造性思维，培养发散思维能力.

第3步：清晰而全面地引导学生归纳总结

上一阶段，只停留在对解决例题的模仿阶段，而有效的例题学习不能单纯地依赖模仿与记忆，因此在解题后，要引导学生主动地梳理解题思路、方法，或通过例题得到的结论，让学生面对类似问题的时候有独立解决的能力.比如，解这道题关键用到菱形的边、角、对角线的性质，通过求面积可以得到结论：菱形的面积是对角线乘积的一半.由于菱形是特殊的平行四边形，面积也可以用底乘以高求得.在这里学生的易错点是用对角线算面积的时候，会忘记乘以二分之一.教师不但要讲清楚为什么要乘以二分之一，而且还要强调乘以二分之一的重要性，防止学生在计算的时候出错.一方面，由于同一个菱形的面积有两种算法，所以可以用等面积法求菱形的高、一条对角线或边；另一方面，还能把这种求面积的方法推广到所有的对角线相互垂直的四边形中，即所有对角线相互垂直的四边形都可以用对角线乘积的一半算面积，故后面即将学到的正方形面积也可以那么算.这里的两种解法又存在内在的联系：由于菱形的对角线把菱形分成了四个全等的直角三角形，所以一个等边三角形实质上是由两个含30°角的全等直角三角形拼凑而成的；第二种解法的思路是把两个含30°角的Rt△拼凑在一起得到等边三角形.这样就找到了两种解法中知识的内在联系，让学生能够洞察问题的深层结构.通过上述梳理、总结，不但让学生掌握了这道题的解法，还学会了所有此题涉及的知识点.而教师也深度分析了教材，把这道例题中要传达的思想、方法、深层知识点等全部挖掘出来.

第4步：“借题发挥”，对例题进行深度与广度上的拓展

从历年的中考试题来看，有的试题源于课本例题的模型，因此要在例题归纳反思之后，有目的地对例题进行深度与广度上的拓展.在深度上，可以通过变化例题的条件、结论、背景等方式拓展；在广度上，可让例题考查的知识点与其他知识综合，拓宽知识的覆盖面，让学生学会化归思想，把若干个数学问题，转化为用一个或几个数学知识点来解决.

对于这道例题，我进行了如下拓展：

1.（菱形面积算法的直接应用）如图2，在菱形ABCD中，BD=6，AC=8，求菱形的面积________，周长_________.（出自人教版八年级《数学》下册P57练习第2题）

2.（等面积法求菱形的高）如图3，四边形ABCD 是菱形，AC=8，BD=6，DH⊥AB 于点H，求DH_____.（出自人教版八年级《数学》下册P61练习第11题）

3.（等面积法求菱形的一条对角线）如图4，菱形ABCD的边长是2 cm，E 是AB 的中点，且DE⊥AB，则对角线AC的长为_______cm.

图2

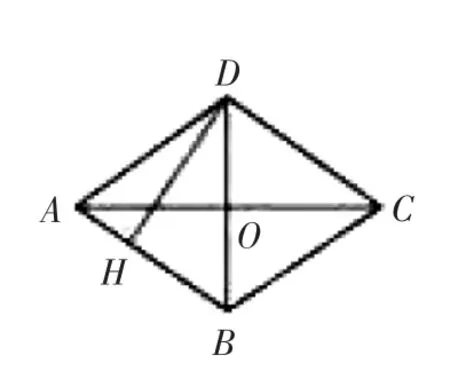
图3

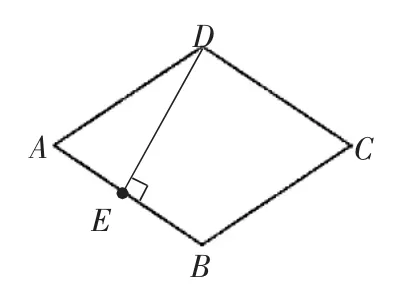
图4

4.（菱形性质与最短路径问题相结合） 如图5，在边长为6 cm 的菱形中∠DAB=60°，E 为AC上一动点，当E 运动到某个位置时，BE+DE 有最小值，这个最小值是____________.

5.（用菱形的性质证明边或角相等）如图6，在菱形ABCD 中，过点D 做DE⊥AB 于点E，做DF⊥BC 于点F，连接EF.

求证：

（1）△ADE≌△CDF；

（2）∠BEF=∠BFE。

6.（菱形的性质与直角坐标系结合，求点的坐标）如图7，在平面直角坐标系中，已知四边形ABCD 为菱形，且A（0，3），B（-4，0）.求C、D 两点的坐标.

图5

图6

图7

设计意图：通过例题的层层变式，不但让学生对菱形性质的认识又深了一步，也培养了学生举一反三的能力.这样做，不但让学生真正会一题、通一片，而且深入理解了所学知识的内涵与外延，还让学生站在一个新的高度上来看数学，从而提升他们的数学解题能力.

第三环节：课后反思

反思是开启数学智慧的钥匙，不但让学生有“量”的积累，更可以达到“质”的飞跃.孔子云：学而不思则罔，西方数学教育家弗赖登塔尔也指出：反思是数学活动的核心和动力.所以，我们要引导学生在解答例题之后，从解题思路、易错或易混淆的地方、类似题目、情感体验四个方面做好反思.

首先，对解题思路、方法、解答等方面进行反思，以提高学生解决数学问题的能力，培养学生具体情况具体分析的能力.对例题的解题思路进行反思：题目问了哪些问题？这些问题与哪些条件相关？要解决问题，先求什么，再求什么？对解答方法进行反思：解决问题用了哪种方法？遇到哪些情况时可以用此方法？能否创新解题方法？对解答的过程是否严密进行反思：解答过程在表述上是否清楚简洁？长此以往，既避免学生出现只会做教师讲过的题，对新题缺乏变通的能力，又提高了学生独立解决数学问题的能力.

其次，对易错、易混淆的知识点进行反思，增强学生识别“陷阱”的能力.学生的学习过程不可能一帆风顺，更不可能人人都做对所有的数学题.在整个学习过程中学生会出现各种各样的错误.面对学生的错误，我们要善于引导他们反思出错的原因，避免下次再出现同样的错误.学生在对错题进行分析和纠正时，对知识又有了新的认识，巩固了知识点和概念，充分认识到自己知识体系中存在的漏洞和误区，从而促进其对知识体系的修正和完善.大量教学实践证明，学生对易错之处进行反思，所取得的效果是显而易见的，不但能为学生未来解决问题提供思路，还能帮助他们养成良好的思维习惯.

再次，对类似题目进行反思，发现知识的内在联系.数学与其他学科不同，学生需要通过适量的练习才能加强对知识点的巩固.无论是教科资料还是市场上的习题册，对同一个知识点的考查，都会出现类似的题目.教师要从中挑出类似的经典题目让学生解答，通过做题，发现它们的异同点和内在联系，总结出同类题目的解题思路和所运用的知识点.

最后，在情感体验处反思.大多数教师注重上述三方面的反思，却忽视了学生对情感体验的反思，而正是学生对数学的情感体验，影响着学生学习数学的兴趣、热情、毅力、品质，这些因素又决定了学生在学习数学的道路上能否走得更好、更远.整个解决例题的过程，不仅是一个知识运用、技能训练的过程，还是一个伴随着交往、创造、追求，以及情绪的喜、怒、哀、乐变化的综合过程.学生解决数学问题时，可能是独立思考所得，也可能是通过合作协同解决.无论是顺利解决简单数学题的那种“思路畅通解题快，一时做尽所有题”的轻松惬意，还是解决了较难的压轴题的那种“会当凌绝顶，一览众山小”的自豪，或者是对百思不得其解的题的那种“白发三千丈，缘愁似个长”的忧愁苦涩，又或者对最后思而得解的题的那种“山重水复疑无路，柳暗花明又一村”的喜悦，都是数学解题中独特的情感体验.在情感体验的过程中，加强了学生学习数学“天生我材必有用”的自信心，激发了学生学习数学的兴趣，点燃了学习热情，磨炼了毅力，形成了良好的学习品质.

“三环四步法”让我们在例题教学中，既把握了全局，把例题的导向性和示范性充分地发挥出来，把例题的功能和价值最大化，又把例题教学的细节落到了实处，真正实现了通过例题教学达到“做一题，懂一类，通一片”的目的，最终提高了课堂教学效率和教学成绩.