探析高考试题中Kc、Kp、Kx的计算方法

陕西 葛秋萍 李歆瑞

《普通高等学校招生全国统一考试大纲的说明》中对化学平衡常数的考查提出了明确的要求：“了解化学平衡常数(K)的含义，能利用化学平衡常数进行相关计算”。近年来的高考化学试题对这一要求的落实率为100%，Kc、Kp、Kx三类平衡常数的计算已然成为年年出现的高频考点，虽然教师和学生都知道这一点，也都把平衡常数的计算当做重点来复习，但学生对此考点的答题情况并不乐观。针对这种答题现状，笔者试图通过例题分类来阐述Kc、Kp、Kx三类平衡常数的计算方法，帮助学生形成解决此类试题的一种清晰的、可重复操作的思维模型，有效击破这三类平衡常数的计算。

一、认识平衡常数

1.Kc、Kp、Kx三种平衡常数的含义

人教版普通高中课程标准实验教科书“化学反应原理”中关于化学平衡常数的定义为“在一定温度下，当一个可逆反应达到平衡时，生成物浓度幂之积与反应物浓度幂之积的比值是一个常数，这个常数就是该反应的化学平衡常数，简称平衡常数”。由于平衡常数是用平衡时各物质的物质的量浓度来计算的，因此又称为浓度平衡常数，用符号Kc或K表示。

研究还发现：若将上述定义中各物质的平衡浓度用平衡时各物质的分压(分压=总压×物质的量分数)来代替进行计算，也可得到一个常数，该常数称为反应的分压平衡常数，用符号Kp表示。同理，若用平衡时各物质的物质的量分数(物质的量分数=某组分的物质的量÷总物质的量)来代替上述定义中各物质的平衡浓度，得到平衡常数的一种新的表达形式，本文中我们暂且称之为反应的物质的量分数平衡常数，用Kx表示。

2.Kc、Kp、Kx三者之间的关系

我们以中学阶段常考的两种反应类型来说明三者之间的关系。

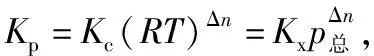
二、典型试题分析

1.浓度平衡常数(Kc)的计算

【分析】解决本题可分为以下三个步骤：

第一步：确定c(HCl)∶c(O2)=1∶1时的对应曲线。相同条件下进料浓度比c(HCl)∶c(O2)越大，HCl的转化率越低；进料浓度比c(HCl)∶c(O2)越小，HCl的转化率越高。由此可知，三条曲线中，最上面一条是c(HCl)∶c(O2)=1∶1的变化曲线。

第二步：确定HCl的平衡转化率。由图像可知：400℃，c(HCl)∶c(O2)=1∶1时，HCl的平衡转化率为84%，即0.84。

第三步：计算平衡常数。本题涉及的相关量，可用三段式法来计算。

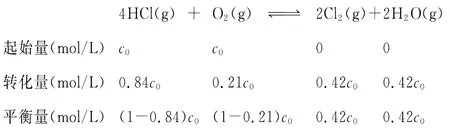
【模型建构】解决此类问题的思维模型：

第一步：确定反应条件与曲线的对应关系。根据反应特点、反应条件、物理量的变化确定反应条件与曲线的对应关系。

第二步：确定反应条件与曲线上点的对应关系。

第三步：利用三段式法求解平衡常数。依据题意，找出三段式中各物质的对应物理量，并列式进行求解。

2.分压平衡常数(Kp)的计算

【分析】本题仍用三段式法来解决，但有两种解法。

方法一：设起始加入反应物的物质的量均为1 mol，到达平衡时，I2(g)的转化量为xmol。

起始量(mol) 1 1 0 0

转化量(mol)xxx2x

平衡量(mol) 1-x1-xx2x

方法二：由阿伏加德罗定律可知：恒温恒容时，气体的压强之比=气体的物质的量之比，所以在三段式法中可以直接用气体的分压来进行相关计算。因为起始时总压为105Pa，且碘和环戊烯的物质的量相等，所以I2(g)和环戊烯的起始分压均为5×106Pa。

起始量(Pa) 5×1065×1060 0

转化量(Pa)xxx2x

平衡量(Pa) 5×106-x5×106-xx2x

解得：x=2×106

【拓展】由前面的分析可知：Kp=Kc(RT)Δn，本题能否先计算出Kc，再由此公式推导出Kp呢？

对于反应前后气体分子数变化的反应，Kc只能由各物质的平衡浓度来计算的。本题并未给出刚性容器的体积及起始时各反应物的物质的量，无法计算平衡时各物质的物质的量浓度，因此，由现有已知条件不能计算出Kc，也就无法由公式Kp=Kc(RT)Δn推导出Kp。相反，如果本题中给出刚性容器的体积及起始时各反应物的物质的量，则可先用三段式法求出Kc，再利用Kp=Kc(RT)Δn求出Kp，其中R=8.314 kPa·mol-1·K-1，这里不再赘述。

【模型建构】解决此类问题的思维模型有三种：

模型一：先用三段式法计算出平衡时各物质的物质的量，再根据分压=总压×物质的量分数，计算出各组分物质的平衡分压，最后将各物质的平衡分压代入平衡常数表达式中进行计算。

模型二：直接用分压来表示三段式中各物质的起始量、变化量和平衡量，再将各物质的平衡分压代入平衡常数表达式中进行计算。

模型三：若能用三段式法求出Kc，则可利用Kp=Kc(RT)Δn求出Kp。

3.物质的量分数平衡常数(Kx)的计算

【分析】解决本题可分为以下三个步骤：

第一步：确定348 K时的对应曲线。其他条件不变时，温度越高，反应速率越快，达到平衡的时间越短，因此图像中曲线变化的标志为先出现拐点，即“先拐，先平，数值大”。由此可知，三条曲线中，①是348 K时的变化曲线。

第二步：确定乙酸甲酯的平衡转化率。由图像可知：348 K时，乙酸甲酯的平衡转化率为64%，即0.64。

第三步：利用三段式法求解平衡常数。依据题意，找出三段式中各物质的对应物理量，并列式进行求解。

348 K时，设起始投入反应物的物质的量均为1 mol，则有：

起始量(mol) 1 1 0 0

转化量(mol) 0.64 0.64 0.64 0.64

平衡量(mol) 1-0.64 1-0.64 0.64 0.64

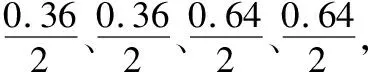
【模型构建】解决此类问题的思维模型：

第一步，确定反应条件与曲线的对应关系。根据反应特点、反应条件、物理量的变化确定反应条件与曲线的对应关系。

第二步，确定反应条件与曲线上点的对应关系。

第三步，用三段式法计算出平衡时各物质的物质的量，再根据物质的量分数=某组分的物质的量÷总物质的量，计算出平衡时各物质的物质的量分数，并将其代入平衡常数表达式中进行计算。