数形结合让数学学习可视化

张卫星

摘    要  数形结合就是把抽象的数学语言、数量关系和直观的几何图形、位置关系结合起来，通过以形助数或以数解形使复杂问题简单化、抽象问题具体化，从而让数学学习可视化。让数学学习可视化的策略有：让概念可视，让算理可视，让数理可视，让规律可视，让过程可视，让思路可视，让策略可视。

关键词 数学教学 数形结合 数学学习 可视化

可视化，即让抽象的数学道理、数学思考和数学思维显性化，强调学生可以通过动手操作让数学道理摸得着，通过语言表达让数学思考听得到，通过直观表征让数学思维看得见。数形结合就是把抽象的数学语言、数量关系和直观的几何图形、位置关系结合起来，通过以形助数或以数解形使复杂问题简单化，抽象问题具体化，从而让数学学习可视化。由此可见，数形结合是实现数学学习可视化的重要手段。借助数形结合，可以促进学生的深度学习，从而形成和发展学生的数学核心素养。

一、让概念可视

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式。数学概念比较抽象，有时候不容易理解。而借助数形结合，可以把抽象的数学概念可视化，让学生在不知不觉中理解其本质属性。

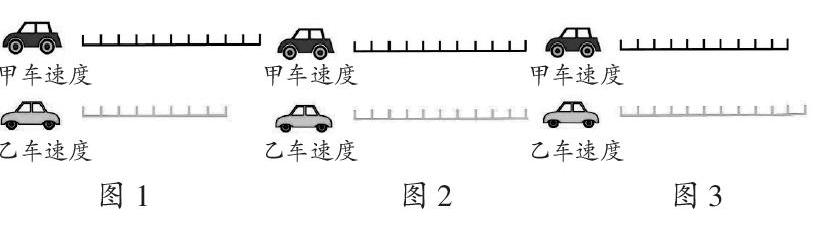
例如，人教版《数学》六年级上册“百分数的意义”一课，学生对“表示一个数是另一个数的百分之几”这一内涵容易理解，也容易理解表示部分与整体关系的百分数（不大于100%），而对表示两个独立量之间倍数关系的百分数（可以大于100%）难以理解。为此，笔者借助课件的动态演示设计了如下三张图片（见图1、图2、图3），让学生说说乙车速度各是甲车速度的百分之几？

图1中，甲车速度平均分成10份，乙车速度具有相同的8份，学生容易说出乙车速度是甲车速度80%，表明乙车速度慢、甲车速度快。借助课件动态演示，乙车速度延长至相同的10份（见图2），学生也容易说出乙车速度是甲车速度100%，表明乙车速度和甲车速度一样快。继续借助课件动态演示，乙车速度延长至相同的11份（见图3），这时学生会感觉到乙车速度比甲车速度快，借助80%和100%这两个百分数产生的经验，学生自然而然会说出乙车速度是甲车速度的110%。在此基础上，笔者适时追问：之前说百分数不能大于100%，为什么现在又可以了？然后师生一起找出原因：因为现在的乙车速度是甲车速度的1.1倍，所以百分数大于100%。在此基础上，顺势提炼出这样的结论：当百分数表示部分与整体的关系时，百分数不能大于100%;当百分数表示两个独立量之间的倍数关系时，百分数可以大于100%。这样，借助数形结合，突破了教学的难点——表示倍数关系的百分数，从而让百分数的概念建构更加完整、更加深刻。

二、让算理可视

計算教学看似简单，实则不然。唯有让学生真正理解算理和算法，才算教学成功。而算理又是算法的前提，因此计算教学的核心是让学生理解算理。而算理具有一定的抽象性。若能借助数形结合，则可以让抽象的算理可视化，从而让学生轻松理解。

例如，在教学人教版《数学》四年级下册“除法的运算性质”一课时，笔者设计了如下两张幻灯片（见图4、图5），然后借助其动态演示，学生就能较好地理解其算理了。

图4中，笔者以长方形图片为载体，先平均分成5份，再平均分成2份，最后结果跟直接平均分成10份是一样的。这个动态演示其实是从除法意义的角度来思考的，学生容易理解，从而让学生知道一个数连续除以两个数（0除外），可以把两个除数先乘起来，让学生初步形成除法运算性质的模型。图5中，以第一个圆形图片为载体，借助动态演示，先把它平均分成4份，再把它平均分成2份，最后结果跟直接平均分成8份是一样的，从而验证a÷4÷2=a÷（4×2）这一除法运算性质的初步模型，进而提炼出a÷b÷c=a÷（b×c） （b、c≠0）这个除法运算性质的第一个正式模型。在此基础上，笔者继续用第2个圆形图片为载体，让学生感受把一个圆先平均分成4份、再平均分成2份，和先平均分成2份、再平均分成4份，结果是一样的——把圆平均分成8份。在此基础上，顺势提炼出a÷b÷c=a÷c÷b（b、c≠0）这一除法运算性质的第二个正式模型。

三、让数理可视

数本身就比较抽象，有些数学生真的很难理解。针对一些学生难以理解的数，不要一味讲解，而应努力想办法让它可视化。若能将某些数可视化，学生就能真正理解数理，从而大大提高学习效率。当然，让数理可视的前提是教师自己要先理解数理。

例如，在教学人教版《数学》四年级下册“小数的近似数”时，对近似数末尾的0为什么不能去掉，用言语很难讲清道理。为此，笔者设计了如下的线段图（见图6）。

借助线段图，学生能够明白近似数是1的小数范围是：大于等于0.5而小于1.5;而近似数是1.0的范围是：大于等于0.95而小于1.05。这样一来，学生就可以感受到近似数1.0和近似数1的意义完全不同，那么学生就不会随便把近似数末尾的0去掉了。同时借助图片，学生也能理解近似数是1的取值范围比较大，近似数是1.0的取值范围比较小，从而理解保留的小数数位越多，精确度越高，越接近实际数据这一道理。同时，学生通过观察图片也能理解一个近似数是1.0或1的小数的范围要从“四舍”和“五入”两个角度去找，从而明白“找原来最小的数要从‘五入方向找，找原来最大的数要从‘四舍方向找”这一道理。

四、让规律可视

数学规律是通过观察和思考提炼出来的一种普遍的数学现象，比较抽象。理解数学规律需要数学智慧的参与。只有深刻理解数学规律的表象，才能真正理解其内涵。因此，借助数形结合让抽象的数学规律直观可视，就可以让学生快速理解。

例如，在教学人教版《数学》五年级上册“三角形的面积”时，“等底等高的三角形面积相等”这一规律，单凭几个例子很难让学生信服。为此，笔者设计了如下的练习（见图7）。