立体几何中活动经验的类型及动手操作策略

福建 吴志鹏 陈玉兰

数学基本活动经验是指活动中经历了观察、操作、实验、思考等过程，形成一种有助于解决相似问题的思路或技能。“动手操作”是数学基本活动之一，学生通过“动手操作”，积累相应的数学活动经验，操作是技能由陌生到成熟再到灵活运用的重要途径，由于活动经验具有内隐性，只有通过列举与描述，使之外显才能发挥经验的价值，才有助于指导学生的学习.在立体几何的学习中特别是解决某些与位置相关的几何问题时，活动经验有着不可替代的作用和价值，在学习和考试的过程中，如能根据活动经验类型，通过观察、操作、实验，建立直观模型并获得有价值的结论，对于正确判断点、线、面的位置关系、相关距离的最值及其运动时所形成的轨迹等问题都有着很好的示范作用，同时也能减少由于空间想象偏差而造成的失误以及减少作图所花费的时间.本文通过对几类常见的立体几何问题进行扫描，引导学生利用一些简单的考试工具及用品，动手操作实验，快速获取正确的结论.

一、“搭建模型”研究“点、线、面位置关系”的活动经验

【例1】已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是

( )

A.若α，β垂直于同一平面，则α与β平行

B.若m，n平行于同一平面，则m与n平行

C.若α，β不平行，则在α内不存在与β平行的直线

D.若m，n不平行，则m与n不可能垂直于同一平面

【解析】解决点、线、面这三个元素的位置关系，特别是元素比较多时，作相应的直观图较为复杂，考试时借助考试工具如用笔芯、铅笔等替代直线，用试卷、桌面等替代平面，这样就能轻而易举地搭建出题目所给元素的位置模型来验证位置关系的正确与否.对于解决此类选择题通常采用排除法，即构建与结论相对的位置关系，判断由条件是否也能获得这种位置关系，如能，则结论错误，否则结论正确，即举反例说明选项的错误.如例1的A选项，用试卷和桌面构建两个相交平面，再验证是否能找到一个平面与这两个平面垂直，结论是能够找到，故A不正确；B选项，用两根铅笔构建两条异面直线，此时易构建出与桌面平行的模型，故B不正确；C选项，α与β相交，在α平面中构建与α，β交线平行的直线，即可得直线与β平行，故C不正确；D选项，构建两根笔与桌面垂直的模型，则两笔一定平行.故其逆否命题“若m，n不平行，则m与n不可能垂直于同一平面”是真命题，所以D选项正确，故选D.

变式：设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β，

( )

A.若l⊥β，则α⊥βB.若α⊥β，则l⊥m

C.若l∥β，则α∥βD.若α∥β，则l∥m

【答案】A.

【评析】此类试题在高考中较为常见，由于四个选项所构成的空间位置比较多种，作空间图形显然更花费时间也更容易出现直观想象的偏差，因此在考试过程中我们可以利用手中的工具，如笔、直尺、三角板、试卷、桌面及教室等构建相应的空间模型，这样进行位置关系的判断比在纸上作图更直观，更高效.

二、“折叠与展开”研究“变与不变”的活动经验

【例2】下图是棱长为1的正方体平面展开图，则在这个正方体中，以下结论错误的是

( )

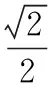
B.AB与BF所成的角为60°

D.EF与MC是异面直线

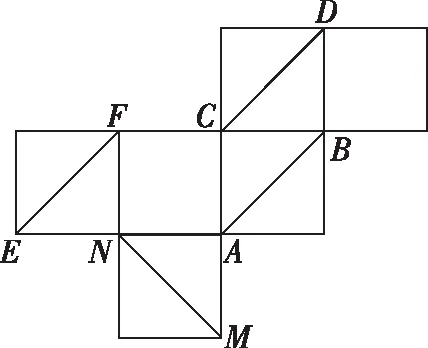
【解析】为考查空间中角和线段的位置变化情况，命题者经常会将图形展开或折叠，让学生通过折叠还原成空间图形或展开成平面图形再来判断.折叠后与展开图的哪些面是对应的？哪些角是对应的？又有哪些顶点是对应的？这些都要求学生要有较强的空间想象能力，给空间想象能力弱的学生则带来很大的挑战，想让他们解决此类问题其实也不难，关键是要弄清哪些量是变的，哪些量是不变的，如果能借助简单工具动手操作，如用小刀将方块橡皮擦切成可立的长方体薄片替代正方体的各个面，分别按展开图放置，再折起还原成正方体就能轻而易举地找到展开图与原图形对应的点和发生变化的点.观察折起的图形，此时问题的难度得到了有效的降低，易选D.

变式：一个正方体的平面展开图及该正方体直观图的示意图如图所示.在正方体中，设BC的中点为M，GH的中点为N.

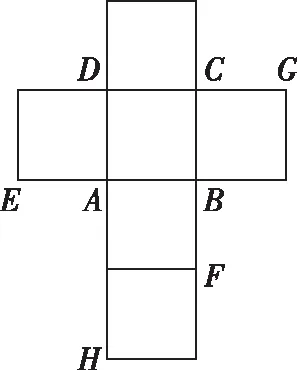
请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；

【答案】F在点B上方的顶点处，G在点C上方的顶点处，H在点D上方的顶点处.

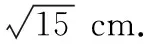
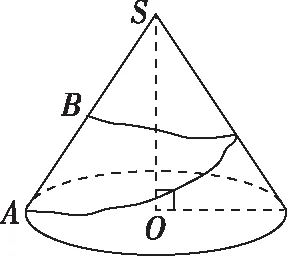
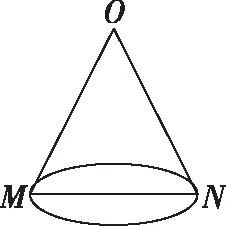
变式：如图，已知O为圆锥的顶点，MN为圆锥底面的直径，一只蜗牛从M点出发，绕圆锥侧面爬行到N点时，所爬过的最短路线的痕迹(虚线)在侧面展开图中的位置是

( )

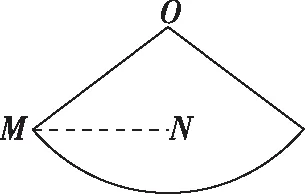
A

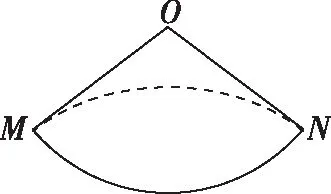
B

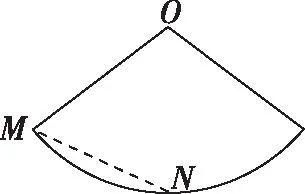
C

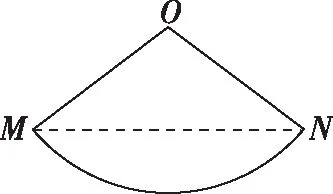
D

答案：C.

【评析】对于研究“变与不变”的问题，我们只需利用简易工具如橡皮擦、软塑料的量角器、试卷(不是答题卡)等依样构建数学模型，再通过折叠或展开，寻找前后相应点的位置，这样可快速对展开图进行还原，或将立体几何图形进行展开，这样看图就更直观、清晰，减少因对应关系偏差而出现的失误，观察所需要的元素在折叠与展开过程经历“变或不变”，更好地助力相关几何问题的解决.

三、“运动旋转”研究“过程变化”的活动经验

( )

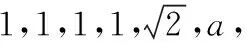
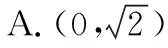
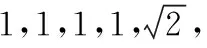
【评析】三角板作为我们作图时常用的工具，其三个角分别为30°,45°,60°的特殊角，边角关系特殊性彰显其具有丰富的内涵，经常作为命题者命题的来源，在三角函数、立体几何、平面几何以及解析几何中均有出现，由边角的这一特殊关系联想到三角板，并利用这个工具动手操作、研究△BAC绕着斜边BC旋转，在这个过程中观察点A与点D的距离变化情况，并获得距离取值的范围.

【例5】如图，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是

( )

A.直线 B.抛物线

C.椭圆 D.双曲线的一支

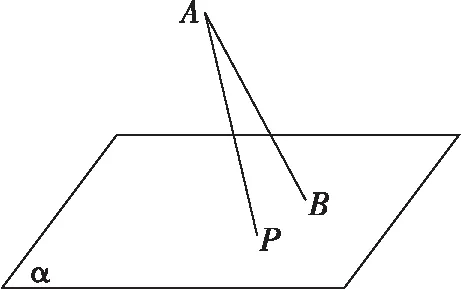
【解析】由题可知∠PAB=30°，当P点在平面α上运动时，可寻得一个含有30°角的三角板进行替代，将斜边固定，另一直角边绕斜边旋转形成一个圆锥，并想象用一个平面去截圆锥所得的图形是什么？易知当平面与圆锥的高垂直时，所得截面为与底面平行的圆，否则为椭圆.本题用一个与圆锥高成60°角的平面截圆锥，所得图形为椭圆，故选C.

【评析】对于旋转问题，一般表现为某个图形围绕着某个点或某条直线进行旋转，有时可以借助数学作图工具，动手实验操作，观察旋转时的图形变化情况以及所求目标在旋转时的位置，通过动手实验操作获得直观、感性认识，进而得出正确的结论，有效解决需要通过证明才能获得结论的问题，实用而又高效.