例说三角形面积最值的思维视角

广东 闫 伟

三角形面积的最值问题一直是各类考试中的热点和难点，因其内涵丰富，灵活多变，常令学生望而生畏.本文拟从这类问题的思维视角作一些举例说明，以资参考.

三角形面积的最值问题一直活跃在各类考试中，因其解法灵活，思维跨度大，故常常令学生“望题兴叹”.该类试题往往聚焦三角形的边和角这两个基本元素，综合考查正、余弦定理及平面几何的性质等知识点，同时渗透函数、不等式、平面向量等内容，突出考查学生的数学运算、逻辑推理等核心素养.笔者经调研发现，尽管多数学生对三角形面积最值问题的基本思路和方法较熟悉，但是大多都依赖于复杂的运算和推理过程，即使答案正确也耗时耗力，无法高效解题.本文拟从这类问题的思维视角进行举例说明，给出思考的方向和可操作的方法，以期给大家启发.

一、基于均值不等式的视角

已知一角及其对边，结合余弦定理直接利用均值不等式求已知角两夹边乘积的取值范围，进而确定三角形面积的最值.

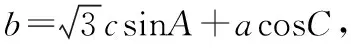
评注:本题先借助正弦定理求出∠A，接着用余弦定理表示三边的等量关系，再利用均值不等式求bc的取值范围，进而求得面积最大值，试题难度不大，解题思路较为自然.

二、基于函数的视角

求一个量的最值常用的方法是将某个变量转化为函数的自变量来处理，于是先将三角形面积表示成某个角或者某一边的函数，再借助函数的性质来求面积的最值.

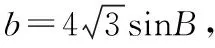
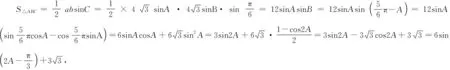
评注：根据已知条件，联想到正弦定理，结合恒等变换将三角形面积表示成某个角的三角函数形式，即y=Asin(ωx+φ)+k形式，再利用三角函数性质求最大值，思路清晰自然，解法较为常规.

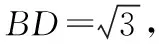
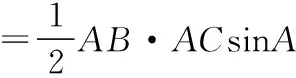
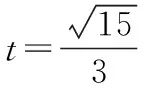
评注：本题的条件相对简洁，都是边与边之间的关系，而正、余弦是处理三角形边、角问题的重要入口，从而自然而然地联想到构造以边为自变量的函数来表示三角形的面积，再利用函数的性质可快速有效地解决最值，体现了函数思想的妙用.

三、基于坐标运算的视角

在三角形面积的最值问题求解中，通过建立平面直角坐标系，把三角形中的边角条件“坐标化”和“解析化”，从坐标运算的角度来解题，可以避免繁杂的逻辑推理过程.

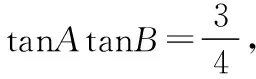
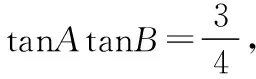
评注:因题中条件过于简洁，仅已知一边和两角的正切值乘积，如果纯粹从三角形中边角关系结合正余弦定理将很难入手，相反通过建立平面直角坐标系进行转化能快速锁定C点的运动轨迹，从轨迹图形中易看出三角形的高即C点纵坐标绝对值的大小，借助坐标运算使得解题过程直观、简洁，极大地降低了试题难度.

四、基于平面向量的视角

平面向量具有“数”和“形”的双重性，是沟通几何、代数和三角的重要工具，借助平面向量基本定理建立三角形中边与边之间的等量关系式再结合均值不等式确定三角形两边乘积的最值，进而确定面积的最值.

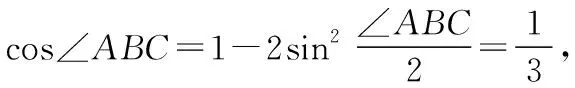
五、基于轨迹的视角

与三角形面积有关的最值问题中条件蕴含的图形往往含有运动的点，解决此类问题的关键是要构建出动点的轨迹，借助轨迹思想求解三角形面积最值往往能够达到出奇制胜，化繁为简的效果.

【例6】△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB，且b=2，则S△ABC的最大值为________.

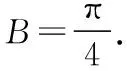
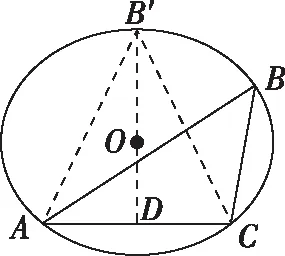
评注：本题以“已知一边及其对角”模型为载体求三角形面积的最大值，考查正、余弦定理和面积公式等知识，解题思路宽泛，可以利用均值不等式或关于角的三角函数来求解，本解法的优点在于根据角B及对边确定B点的轨迹是圆上的一段优弧，揭示了问题的本质，使得解题过程更加简洁明了.

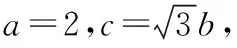
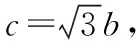
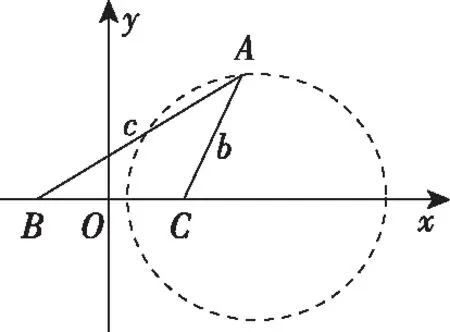
评注：本题的背景是阿氏圆：设A,B为两定点，动点P满足PA=tPB，当t≠1时，动点P的轨迹是阿氏圆，根据阿氏圆的定义确定A点的轨迹方程，从而将面积最大值问题转化到求A点到x轴距离的最大值问题；若借助其他解法，都不如轨迹法运算量少，简单直观.

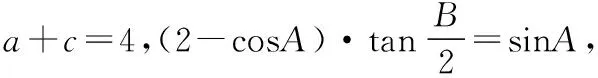
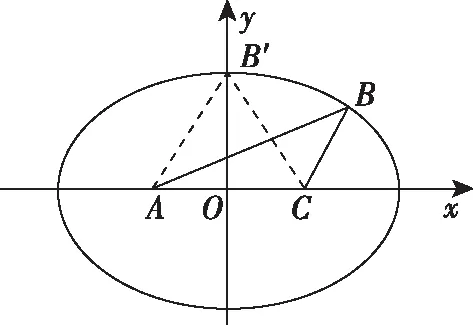
评注：本题若用常规解法，比较复杂，要借助半角公式和海伦公式，运算相当繁琐，相反先借助椭圆定义求B点的轨迹，再结合椭圆的特征确定三角形面积取最大值的位置，巧妙地避开复杂的代数运算，起到四两拨千斤的效果.

六、基于平面几何的视角

解三角形有关的问题本质上是平面几何问题，借助平面几何知识结合几何图形的特征将问题进行转化，可以顺利求解三角形面积最值，实现高效解题.

【例9】在△ABC中，∠BAC=60°，点D在线段BC上，且BC=3BD，AD=2，则S△ABC的最大值为________.

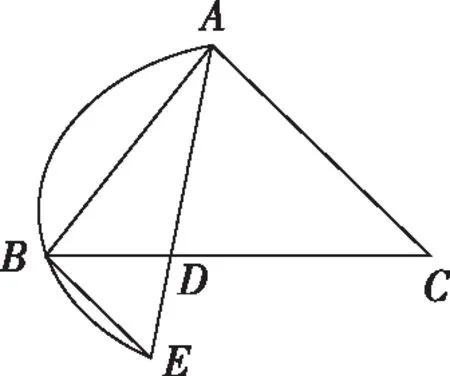
评注:从本质上看解三角形也是平面几何的知识，像本题这一类动态三角形问题都有着平面几何背景，通过平面几何中相似三角形知识将原问题转化为一个基本问题：已知三角形中的一角及其对边，求面积的最大值，巧用外接圆来解三角形面积，体现了化归与转化的思想，让学生感受到任何一道难题都可以转化为我们熟悉的问题.

七、基于特殊结论的视角

先给出一个特殊结论：在四边形ABCD中，有AB·CD+AD·BC≥AC·BD，当且仅当四边形A,B,C,D四点共圆时，等号成立.该结论是平面几何中的重要结论——广义托勒密定理.

【例10】已知△ABC是以AC为斜边的等腰直角三角形，D为△ABC外一点，且CD=AD=2，则△BCD面积的最大值为________.

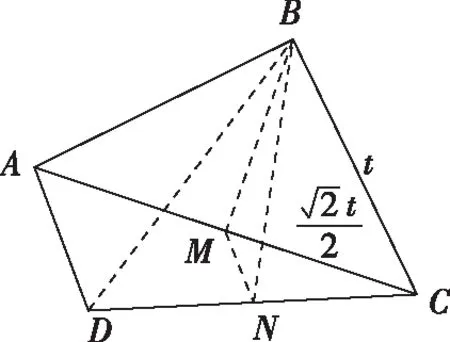
评注：本题借助平面几何知识，在底边确定的情形下，一定有底边上的高不大于底边上的中线，故在求高的最大值时转化到求中线的最大值，再结合广义托勒密定理可顺利求解中线的最大值，进而求得面积的最大值，作为小题，妙借结论解题不失为一种高效的解题方法.