综合区间数Spearman秩相关系数及其应用*

连 强

(郑州市财贸学校 会计系，郑州 450015)

0 引 言

相关性[1]作为概率论和数理统计中的一个重要概念，其在经济管理、工程科学等领域发挥着非常重要的作用。随着研究的不断深入，研究对象呈现出越来越复杂的态势，其不确定性和模糊性也日益增强。为此，许多学者尝试将统计学中的相关性推广到不确定性领域，并取得了一些研究成果。比如，文献[2-5]将相关性推广到了模糊集[6]，建立了模糊集的相关系数，为研究模糊决策提供了非常具有建设性的参考。再如，一些学者研究了直觉模糊集[7]的相关性，建立不同的直觉模糊集的相关系数[8-12]。事实上，这些相关系数大致可以分为两类，一类取值范围为[0,1]，仅能反映出研究对象之间的相关强度，不能反映出相关的正负性；另一类取值范围为[-1,1]，不仅能反映出研究对象的相关强度，而且还能反映出它们之间是正相关还是负相关，此类相关系数与统计学中的相关系数非常类似。

Spearman秩相关是统计学中常用的一种相关性[13]，其通过两组观测值的秩差来定义它们的相关性，为人们研究相关性提供了一种可行的方法。2010年，Szmidt等[14]将Spearman秩相关推广到了直觉模糊集，定义了直觉模糊Spearman秩相关系数，为人们研究模糊领域的Spearman秩相关系数提供了一个很有意义的参考。最近，苏丽敏等[15]将Spearman秩相关应用到区间数决策中，定义了方案与正理想方案之间的Spearman秩相关系数，并根据Spearman秩相关系数的大小实现方案的排序择优。但是，该方法也具有一定的局限性，即仅考虑到每个方案与正理想方案的Spearman秩相关性，而没有考虑到每个方案与负理想方案的Spearman秩相关性。为了消除这种局限性，提出了一种综合考虑方案与正负理想方案之间的Spearman秩相关系数的决策方法，即在TOPSIS方法[16]的启发下，首先，定义了方案与负理想方案的Spearman秩相关系数；然后，在方案与正负理想方案Spearman秩相关系数的基础上，定义了方案的综合Spearman秩相关系数，并证明了其相关性质；最后，提出了基于综合Spearman秩相关系数的区间数多属性决策方法，并通过一个实例说明了所提出方法的可行性。

1 相关概念

下面回顾相关的一些概念，为研究工作做好铺垫。

定义1[1]设(x1,x2,…,xn)，(y1,y2,…,yn)分别为来自总体X,Y的样本，令R(xj),R(yj)分别表示xj,yj在(x1,x2,…,xn)，(y1,y2,…,yn)中的秩，则X与Y的Spearman秩相关系数定义为

其中dj=R(xj)-R(yj),j=1,2,…,n。

定理1[1]设(x1,x2,…,xn)，(y1,y2,…,yn)分别为来自总体X,Y的样本，则X与Y的Spearman秩相关系数r(X,Y)具有以下性质：

(1)r(X,Y)=r(Y,X)。

(2) 若X=Y，r(X,Y)=1。

(3) |r(X,Y)|≤1。

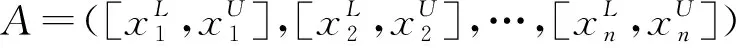
其中：

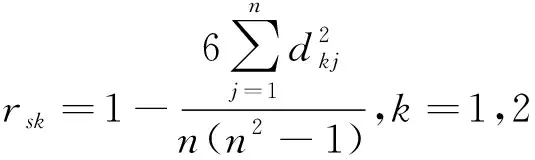
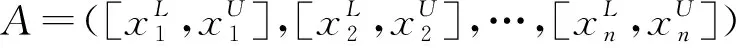
(1)rs(A,B)=rs(B,A)。

(2) 若A=B，rs(A,B)=1。

(3) |rs(A,B)|≤1。

2 基于正负理想方案的区间数Spearman 秩相关系数

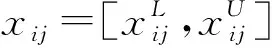
苏丽萍等求出了每个方案Ai与正理想方案A+的Spearman秩相关系数r(Ai,A+)，然后按照r(Ai,A+)的大小对方案排序择优。

其中

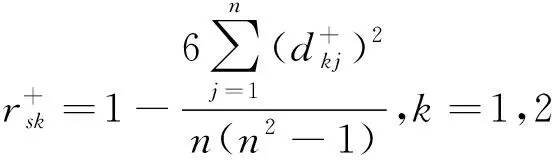
显然，方案Ai与正理想方案A+的Spearman秩相关系数越大，表明方案Ai越优。这与 TOPSIS方法中，方案Ai与正理想方案A+的距离越近，其排序越优极为相似。但是，在TOPSIS方法中,不仅考虑到了每个方案与正理想方案A+的距离，同时也考虑到了每个方案与正理想方案的距离，即TOPSIS方法综合考虑了每个方案与正负理想方案的距离，也即要求不仅每个方案与正理想方案的距离越近越优，而且同时要求每个方案与负理想方案的距离越远越优。

在TOPSIS方法的启发下，下面给出每个方案与负理想方案的Spearman秩相关系数，然后，定义每个方案与正负理想方案的综合Spearman秩相关系数。

其中：

定义5 称

为方案Ai的综合区间数Spearman秩相关系数，其中rs(Ai,A+)为方案Ai与正理想方案A+的Spearman秩相关系数，rs(Ai,A-)为方案Ai与负理想方案A-的Spearman秩相关系数。

综合区间数Spearman秩相关系数具有以下性质：

定理5

(1)rs(Ai,A±)∈[-1,1]。

证明

(1) 由于rs(Ai,A+)∈[-1,1],rs(Ai,A-)∈[-1,1]，故而

3 决策应用

3.1 决策方法

下面给出利用区间数综合Spearman秩相关系数进行决策的具体计算步骤。

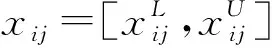
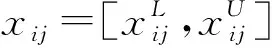
步骤2 根据属性的类型，将区间数决策矩阵标准化，具体方法为

(1) 效益型属性:

(2) 成本型属性:

步骤3 从标准化区间数矩阵M=(uij)m×n中求出正负理想方案，其中

正理想方案:

其中:

负理想方案:

其中

步骤4 求出每个方案Ai与正负理想方案A+,A-的Spearman秩相关系数rs(Ai,A+)，rs(Ai,A-)。

步骤5 求出方案Ai的综合Spearman秩相关系数：

步骤6 根据综合Spearman秩相关系数rs(Ai,A±),i=1,2,…,m的大小对方案进行排序。

3.2 应用实例

例1[15,17]某高校要对4个二级院系A1,A2,A3,A4的财务管理情况进行评价，并制定了5项考核评价指标：二级财务管理制度(c1)、二级财务预算和执行(c2)、二级财务管理的经济责任(c3)、二级财务监督管理(c4)、二级院系财务人员素质(c5)。首先专家使用百分制区间数对各二级院系的财务管理情况进行了打分，然后将区间数属性值进行标准化处理，如表1所示。下面利用本文提出的方法对4个二级院系的财务情况进行评价。

步骤1-2 专家使用百分制区间数构造区间数决策矩阵N=(xij)4×5，然后将区间数决策矩阵N标准化，得到标准化区间数决策矩阵M=(uij)m×n，见表1。

表1 标准化区间数决策矩阵Table 1 Normalized interval number decision making matrix

步骤3 正负理想方案分别为

A+={[0.554,0.765],[0.447,0.943],

[0.670,0.728],[0.538,0.721],

[0.571,0.663]}

A-={[0.240,0.295],[0.149,0.471],

[0.359,0.401],[0.231,0.361],

[0.326,0.368]}

步骤4方案Ai与正理想方案A+、负理想方案A-的Spearman秩相关系数分别为

rs(A2,A+)=0.25，r(A3,A+)=0.4

r(A4,A+)=0.15

步骤5 方案Ai的综合Spearman秩相关系数分别为

rs(A2,A±)=0.05,rs(A3,A±)=0.2

rs(A4,A±)=-0.225

步骤6 由rs(Ai,A±)的值的大小知，方案排序为A3>A2>A1>A4。

若使用仅考虑正理想方案的Spearman秩相关系数方法计算，可得

rs(A1,A+)=0.35，rs(A2,A+)=0.25
r(A3,A+)=0.4，r(A4,A+)=0.15

于是方案排序为A3>A1>A2>A4。

由上面计算可以看到，若仅考虑正理想方案，则得到的方案排序为A3>A1>A2>A4；而综合考虑正负理想方案得到方案排序为A3>A2>A1>A4。由此可知，仅考虑正理想方案与综合考虑正负理想方案得到排序是不同的。由于综合考虑正负理想方案的Spearman秩相关系数方法，既考虑到了每个方案与正理想方案的相关性，同时也考虑到了每个方案与负理想方案的相关性，因此得到的排序结果将会更加符合实际情况。

4 结 语

通过分析现有区间数Spearman秩相关系数的不足，在TOPSIS方法的启发下，综合考虑方案与正负理想方案之间的Speanrman秩相关系数，定义了区间数综合Spearman秩相关系数，并证明了其相关的性质；然后，提出基于区间数综合Spearman秩相关系数的多属性决策方法，并通过高校二级院系财务管理的实例说明了所提方法的可行性。区间数综合Spearman秩相关系数的提出促进了相关系数在不确定决策中的发展，同时对于相关系数在其他不确定决策领域的推广也具有一定的启发意义。