基于多种分布对云南山区风速的综合评估*

夏丽丽, 苏 华

(1.西南交通大学 数学学院，成都 610031；2.四川航天长征装备制造有限公司，成都 610199)

0 引 言

风能是清洁的可再生能源，发展风能对于改善能源结构、保护生态环境等方面有及其重要的意义。中国地形分布复杂，除了沿海地区、高原地区存在丰富的风能源，山区的风能源也很值得研究，本文对云南山区的风速数据进行研究。在实际研究中发现，准确得到风速数据的概率密度函数将减少风能输出估算的不确定性。现在许多概率分布都用于风速分布的研究，张盼盼[1]比较了正态分布和威布尔分布，分析哪种分布函数模拟风速分布的效果比较理想，得到的结果是两参数威布尔分布是拟合风速较好的模型；杨晓鹏等[2]通过数值模拟一年云南风速，对云南风能资源分布进行研究；洪祖兰等[3]对云南省356个测风塔的地理分布以及风速风况特征进行研究；Nage[4]比较了威布尔分布和瑞利分布，从分布的统计分析来看，威布尔分布在拟合概率密度分布方面比瑞利分布更好；Wais[5]提出使用三参数威布尔分布用于拟合风速数据，结果表明：对于零风速的较高概率，三参数威布尔分布与双参数威布尔分布相比给出了更好的结果；Kantar等[6]提出扩展广义Lindley分布可替代风速分布用于评估风能潜力；Morgan等[7]在评估海上风电场时，认为两参数对数正态分布在估计极端风速方面表现最佳；Pishgar-Komleh等[8]在分析Firouzkooh地区的风速数据时，在威布尔和瑞利分布函数的基础上很好地得到了风速的实际值。

本研究的主要目的是评估各类分布对于云南风速的适用性，并确定最适合在云南山区建模的风速数据的分布。本文选取了几种常规分布，应用极大似然方法进行参数估计，选取决定系数R2、Kolmogorov-Smirnov检验、卡方检验、均方根误差(RMSE)和贝叶斯信息准则(BIC)进行拟合优度检验，在直方图画出拟合曲线以及QQ图进行直观分析，并利用所选分布计算各个站点理论风功率密度与实际风功率密度比较相对误差。

1 风速分布

最常用的分布有威布尔分布、伽马分布[9]、对数正态分布、正态分布、瑞利分布[10]，它们的概率密度函数由表1给出。

表1 所选分布的概率密度函数和风功率密度函数Table 1 Probability density function and wind power density function of selected distribution

2 参数估计

常用的参数估计方法有最大似然估计、矩法估计和最小二乘法[7-9]。考虑数据的量比较大，此处选用极大似然估计来进行参数估计。

2.1 极大似然理论

极大似然方法是常用的分布参数估计方法之一，在该方法中，通过最大化似然函数或对数似然函数来估计参数。似然函数是模型参数的函数，由式(1)给出：

(1)

其中,f(vi;θ)是概率密度函数，vi是第i个风速数据，n是数据点的数量，θ是分布的参数向量。为了减小计算的复杂性，通常采用对数似然函数来估计概率分布的参数。对数似然函数表示为

(2)

2.2 模型评估准则

为了评估不同模型在确定风速分布方面的准确性，选择以下5个指标：决定系数R2、卡方统计量χ2、K-S检验、RMSE以及BIC准则进行分布的拟合优度评估[11]。

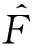
(3)

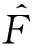
(4)

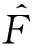
(5)

(4) 均方根误差检验(RMSE)。均方根误差检验(RMSE)描述了观测概率与预测概率之间实际偏差的逐项比较，RMSE值SRMSE越小表示分布拟合越好[1]。均方根误差检验值定义为

(6)

(5) 贝叶斯信息(BIC)准则。衡量统计模型拟合优良性的一种标准，BIC值越小，说明模型拟合越好。BIC值定义为

SBIC=-2lnL+klnn

(7)

其中n是数据的个数，L是似然函数，k是参数个数。

3 案例应用与分析

3.1 数据的来源

数据来自云南山区的4个气象站点，站点0579位于双柏县爱尼山乡(南)，站点8415位于马龙县纳章镇瓦古冲村，站点0229曲靖市富源县墨红镇，站点8013位于云县。在本研究中，使用10 m高度的每10 min平均风速。这些风速数据记录在云南的4个气象站。高度、记录周期、经纬度以及海拔等信息如表2所示。表3列出了各站点中风速数据的最大值、平均值、中值、标准差、偏度系数和峰度系数等统计数据，从表3可以看出，所有偏度系数均大于0，说明风速分布均是右偏分布。

表2 研究站点的地理位置Table 2 The geographical location of the research stations

表3 站点风速数据的描述性统计Table 3 Descriptive statistics of wind speed data at the stations

3.2 拟合结果

3.2.1 模型评估

对于每个站点，基于不同分布，采用极大似然方法估计每种分布的参数，表4中给出了极大似然理论对于混合分布和威布尔分布的参数估计值。表5分别给出双柏县站点、富源县站点、云县站点、马龙县站点包含威布尔分布在内的5个分布，基于RMSE、卡方统计量χ2、K-S检验，决定系数(R2)以及BIC准则，通过式(4)—式(7)进行拟合优度值计算。

表4 所有站点不同分布的参数估计值Table 4 Estimated values of the parameters of different distributions of all stations

表5 所有站点拟合优度检验的值Table 5 All stations goodness of fit test value

从表5中可以看出：双柏县站点基于R2，SK-S、卡方统计量、SRMSE以及SBIC，威布尔分布表现最好；马龙县站点基于上述5个检验得出正态分布表现最好；云县基于5个检验得出威布尔分布和正态分布表现都好，从数值上来看差别不大；富源县站点瑞利分布表现较好，其次是威布尔分布和伽马分布，三者差别较小。为了准确判别云南山区风速最合适的频率分布，考虑引入直方图和QQ图进行更直观的比较。

3.2.2 模型直方图和QQ图的比较

一般来说,样本容量越大，频率分布直方图就会无限接近总体密度曲线，就越精确地反映总体的分布规律，即越精确地反映总体在各个范围内取值百分比。在直方图中画出拟合分布的密度曲线可以直观看出拟合曲线与样本直方图的拟合程度，从而直观地判断分布对于样本数据拟合的优良性。除此之外，在统计学中，QQ(分位数-分位数)是通过图形比较两个概率分布的方法。如果被比较的两个分布相似，则QQ图中的点将大致位于线y=x上。此处QQ图用于比较站点数据与理论分布的拟合程度，图中的点越接近线y=x，则说明该理论分布对数据拟合较好。

针对表4得出的结论，在直方图中画出各个理论分布的密度曲线比较拟合结果。图1—图4分别针对各个站点画出直方图以及数据与理论分布的QQ图，以进行更直观的比较。

由图1—图4可以看出：富源县站点和双柏县站点直方图和QQ图显示威布尔分布更合适在直方图的拟合密度曲线中表现出最好的结果。虽然马龙县和云县的威布尔分布密度曲线和正态分布曲线在直方图中表现有所差别，但是发现二者的QQ图曲线几乎重合在一起。为了对云南山区风速分布的选择更加合理，下面从风功率密度的角度来分析。

4 风功率密度

对于观测区域的风况特征进行分析，有助于估算风能潜力。风功率概率密度函数在风力涡轮机的设计过程和潜在场地可用的风力资源评估过程中都是有用的。在科学文献中，通常使用对应于标准条件(海平面，15 ℃)的恒定值空气密度ρ=1.225 kg/m3。通过叶片扫掠区域Sw以速度V飞行的风力随着其速度的立方增加，因此每单位面积的风流中可用的功率(风功率密度)可表示为[12]

(8)

其中：ρ是空气密度，取决于海拔高度、气压和温度。平均风功率密度基于风速的分布函数f(V)定义为

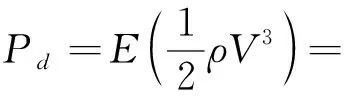
(9)

实际样本的风功率密度计算公式为

(10)

其中：n是观测样本的个数。表6给出了4个站点风功率密度值与真实值的比较结果。

表6 4个站点基于分布的风功率密度理论值与实际风功率密度及其相对误差Table 6 Theoretical values of wind power density and actual wind power density values at four stations and their relative errors

使用真实数据获得的结果与各个分布的解析式获得的结果之间的比较是通过相对百分比误差来评估的，该值显示了对应分布的准确性,定义为

(11)

从表6中可以看出：威布尔分布下的理论风功率密度与实际相对误差富源县为0.53，马龙县为0.05，双柏县为0.09，云县为0.197，故威布尔分布为4个站点中所选分布对于实际分布拟合最好的分布，对于风功率密度的估算最接近实际值。

5 结 论

使用5种常规分布对云南山区风速做拟合，并给出综合评价。拟合优度从数值大小的角度看，威布尔分布、正态分布以及瑞利分布在4个站点呈现较好结果，但数值角度的结果说服力不够强。为了更加直观，选取实际数据直方图与分布密度曲线拟合性进行比较，发现威布尔分布在富源县和双柏县站点呈现较好结果，在马龙县和云县正态分布和威布尔分布的结果都比较好。为了仔细区分，从实际角度出发，利用标准空气密度下风功率密度来比较，根据理论分布数据和实际数据相对误差图可以看出威布尔分布的结果最好。综合上述比较，威布尔分布最适合云南山区的风速。