月面着陆多尺度边缘光流特征提取与跟踪方法

李云天，穆荣军，单永志，崔乃刚

(1. 哈尔滨工业大学航天工程系，哈尔滨150001；2. 中国兵器工业集团航空弹药研究院，哈尔滨150001)

0 引 言

月面着陆按降落时序可大致分为离轨再入、动力下降与最终着陆三个阶段。其中，动力下降段飞行时间最长，空域最广，该段的导航定位精度直接决定了着陆器的最终着陆精度[1]。由于月球尚未建成完备可靠的绝对定位系统，地面测控站与着陆器之间又存在较大的通信延迟，着陆器的导航精度极大程度依赖于惯性测量单元(Inertial measurement unit，IMU)、着陆相机(Landing camera，LCAM)、激光探测与测距(Light detection and ranging，LiDAR)等传感器组成的自主导航系统[2]。其中，LCAM及基于LCAM的视觉导航系统具有造价低、重量轻、功耗小、可同时获取着陆器位姿等优势[3]，和惯性导航系统并列为动力下降段的首选导航系统。

月面着陆视觉导航系统可分为视觉绝对导航系统和视觉相对导航系统两种。视觉绝对导航系统在动力下降过程中使用正下视安装的LCAM获取着陆器当前位置的月面图像及地形特征(如陨石坑特征[4]、阴影特征[5]、混合特征[6]等)，随后通过与现有月面地形数据库匹配，获取着陆器在月球固连坐标系下的绝对位置。中国的嫦娥-4(CE- 4)探测器、美国NASA的“自动着陆与风险规避技术”(Autonomous landing and hazard avoidance tech-nology，ALHAT)、德国DLR的“自动光学相对地形导航”(Autonomous terrain based optical navigation，ATON)等均采用了这一方式。虽然视觉绝对导航系统可获得着陆器在月球固连坐标系下的绝对位姿，但仍存在计算负担重、依赖地形数据库精度、相机斜视情况下匹配困难、平坦区域无法工作、需要耗费大量数据存储空间等缺点。

与之相比，基于序列图像的视觉相对导航系统虽无法获取月球固连坐标系下的绝对位置，但由于具有不依赖月面数据库、在平坦区域能获取充足的特征点，对LCAM朝向无要求等优势，近年来逐渐受到了重视[6-7]。视觉相对导航系统通过提取和匹配序列图像特征，进而最小化重投影误差或灰度误差的方式得到着陆器在两帧图像之间的相对位姿估计。因此特征提取与跟踪的精度和计算效率很大程度上决定了视觉相对导航系统的精度和实时性。

由于陨石坑和石块是月面地貌的主要组成部分，视觉相对导航系统通常采用特征角点(Harris、FAST等)和特征气泡点(SURF、KAZE等)作为跟踪特征。其中，以FAST为代表的特征角点因具有较高的计算效率和良好的光照不变性[8]，被广泛应用于视觉相对导航系统中[9-10]。但传统特征角点方法提取的特征点过于集中，存在特征聚集问题，且在尺度不变性方面仍有待进一步提高。

在完成特征点提取后，视觉相对导航系统还需对所提取出的特征点进行跟踪以确定特征点之间的匹配关系，作为下一步位姿估计的基准。基于描述子的传统特征跟踪方法工作流程如图1(a)所示。首先，基于描述子生成算法计算前后两帧中所有特征点的描述子；为了保证描述子的准确性和鲁棒性，这一过程需要进行大量的统计计算(例如BRIEF描述子需要统计特征点附近256个像素对的明暗分布情况[11])。随后，对于参考帧中的每一个特征点，遍历当前帧中的所有特征描述子，筛选出距离(通常采用马氏距离或汉明距离)最近的特征点作为匹配点对。上述过程的计算耗时通常占整个特征提取和跟踪算法耗时的3/4以上，同时需要大量存储空间记录所有特征描述子，严重降低了相对视觉导航系统的实时性。

由于月球表面不存在大气且动力下降段时间较短，可认为LCAM捕获的序列图像满足灰度不变假设，这为光流法的应用带来了可能，涌现出了若干以Kanada-Lucas-Tomasi(KLT)光流跟踪为代表的，使用光流预测代替特征匹配进行特征跟踪的研究成果[12-13]。由于跳过了特征描述子的计算和匹配过程，基于光流预测的特征跟踪算法计算效率相较基于描述子的特征跟踪算法有了极大提升。但传统光流算法基于小运动假设，对大尺度运动的鲁棒性较差；且求解过程涉及图像二次导数的计算[14]和二维图像平面的匹配搜索[15]，对于系统的计算能力依旧有一定要求。

针对上述问题，本文提出一种多尺度边缘光流(Multi-Scale Edge-Flow，M-EF)特征提取与跟踪方法，工作流程如图1(b)所示。首先采用带方向描述的ORB特征替换传统的FAST特征，并使用多级掩膜方法优化特征点分布。随后，基于图像边缘直方图，采用灰度差平方和(Sum of square grayscale difference，SSGD)滑窗搜索算法分别计算特征点在图像坐标系两个方向上的边缘光流，将二维光流迭代计算问题简化为一维直方图匹配问题，以提高计算效率。同时，通过引入多尺度边缘直方图和迭代搜索算法，在有效抑制大尺度运动下特征点跟踪易丢失问题的同时，将光流计算精度由整像素级拓展至亚像素级。最终，基于嫦娥4号探测器动力下降段LCAM获取的真实图像序列对所提出算法的性能进行了仿真校验。

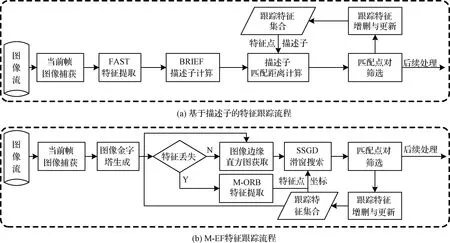
图1 传统特征跟踪算法与M-EF特征跟踪算法流程对比Fig.1 Comparison of working flow between traditional feature tracking method and M-EF feature tracking method

1 多级掩膜ORB特征提取

ORB特征是Ethan Rublee等在FAST基础上，引入方向描述和Harris角点评价提出的一种具有较好旋转和尺度不变性的视觉特征[16]。现有ORB算法在筛选特征点时完全依赖于其Harris评分，而图像强特征附近的特征点通常会具有十分相近的Harris评分。这就带来了特征点聚集问题：大量特征点集中于图像中的一个或某几个强特征区域，其他区域则只存在零散的特征点；分布缺乏均匀性，进而影响后续特征跟踪和位姿估计的精度。

针对这一问题，提出一种构建图像金字塔，并采用多级掩膜(Mask)，分级分批提取特征点的多尺度ORB(Multi-scale ORB，M-ORB)特征提取算法，流程概述如下：

1)以当前帧为底层，逐层下采样(Down Sample)构建图像金字塔；

2)在金字塔的顶层进行ORB特征提取，并根据Harris评分筛选出评分靠前的若干特征点；

3)将所提取特征点的坐标上采样(Up Sample)至下一层；

4)在该层图像上以上采样坐标为圆心绘制圆形掩膜，掩膜内的区域在本层特征提取过程中将被忽略；

5)重复步骤2)至3)直至第0层；

6)从第0层未被掩膜覆盖的图像区域中一次性提取出剩余数量的特征点；

7)将每层提取出的特征点坐标统一上采样至第0层，即为所需的特征点集。

1.1 图像金字塔构建

记需要提取特征点的原始图像为图像金字塔的第0层I0(x,y)，则图像金字塔可通过下述下采样过程构建：

1)扩充第L-1层图像边缘，将图像四周高斯卷积核半窗口大小内的所有像素灰度填充为0；

2)对图像中的所有像素点应用式(1)所示的高斯卷积核G重新计算灰度；

(1)

3)按照式(2)计算第L层图像对应位置的像素灰度值，式中x和y分别为图像点在第L层图像坐标系上的横纵坐标；

(2)

4)重复步骤1-3直到顶层，得到图像金字塔集合{IL}L=0,…,k。

显然，对于金字塔的第k层图像来说，特征检测和光流计算的范围将分别增大4k和2k倍。虽然理论上金字塔层数越多，特征检测和跟踪的鲁棒性越高，但相应的计算负担也会加重。因此在实际应用中，k的取值范围通常为2～4。

1.2 多级掩膜特征提取

所谓多级掩膜特征提取，即在完成图像金字塔的构建后，首先在尺度最小的顶层图像上提取若干特征点；这部分特征点所处的区域在下一个尺度图像的特征提取过程中将被设置为掩膜从而被忽略；循环上述过程直至遍历所有尺度的图像，获得最终的特征点集合。

图2 采用多级掩膜的多尺度ORB提取算法流程图Fig.2 Flow chat of multi-scale ORB extraction method based on multi-level mask

多级掩膜特征提取中最重要的两个参数为每层的特征点数目nL和掩膜半径rm，由于每次下采样后图像尺寸变为原图像的1/4，这里不失一般性地假设每层的特征数目和掩膜半径满足：

nL-1=4nL, (rm)L-1=2(rm)L

(3)

设需要提取的特征点总数为N，金字塔顶层为k层，则第L层需要提取的特征点数目nL为：

(4)

同理，第L层的掩膜半径(rm)L为：

(5)

式中：w和h分别为图像的宽度和高度。

2 多尺度边缘光流特征跟踪

随着相机的移动，像素点在两帧图像之间的运动就像水流一样，故称之为光流(Optical Flow)，单位为pixel/s。由于光流表征了像素点的运动方向和大小，基于光流预测的特征跟踪方法可有效缩小特征跟踪范围，在提高特征跟踪准确度的同时有效减轻计算负担。

基于同一特征区域在前后两帧图像中应具有相似的空间边缘分布这一假设，文献[17]提出了一种基于边缘直方图的光流计算方法——边缘光流(Edge-Flow，EF)。EF算法在小尺度运动下具有较好的跟踪效果和较低的计算耗时，但在大尺度运动下的计算效果并不理想，且只能获得整像素级光流。本文在此基础上，进一步提出了多尺度边缘光流算法(Multi-scale Edge-Flow，M-EF)，在提高大尺度运动下特征跟踪鲁棒性的同时，将光流计算精度由整像素级拓展至亚像素级。

2.1 边缘光流

EF光流计算的核心是图像边缘直方图，而图像的边缘可由图像一阶导数描述。因此在获取序列图像后，分别对前后两帧图像应用式(6)所示的Sharr算子计算图像x和y方向上一阶导数。随后，分别将图像中所有像素点的一阶导数值按列、按行求和作为边缘数值，即得到图像在x和y方向上的边缘直方图。

(6)

显然，相同图像点在两帧边缘直方图上应具有相同的边缘点数目。但由于直方图中具有相同边缘数值的坐标位置并不唯一，具有相同边缘数值仅是两个坐标位置是同一特征点的必要而非充分条件。因此，需要采用图3所示的灰度差平方和(SSGD)滑窗搜索，综合比较待不同坐标位置周围的灰度分布，减少误匹配，提高光流计算精度。

记q为图像点在参考帧边缘直方图中的坐标，则其在当前帧边缘直方图中的坐标t应满足：

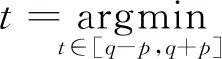
(7)

式中:p为滑动搜索区间的半长度，(q,t,s)为灰度差平方和(SSGD)函数：

(8)

式中:hr(·)为参考帧的边缘直方图，hc(·)为当前帧的边缘直方图，s为搜索窗口的半长度。

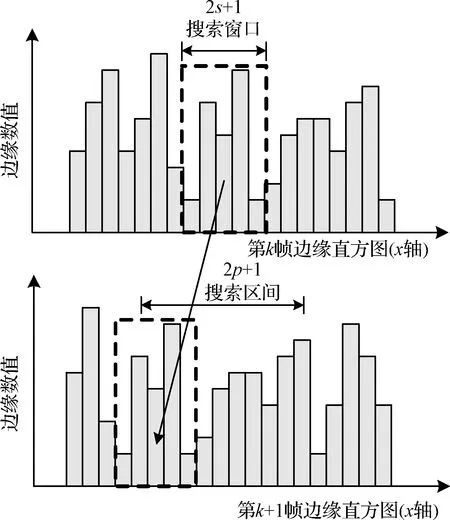
图3 边缘光流SSGD滑窗搜索算法Fig.3 SSGD based sliding window search for EF

2.2 多尺度边缘光流

原始EF算法存在两个缺陷:1)为了跟踪大尺度运动，需要设置较大的搜索窗口和搜索区间，一定程度上增加了计算负担；2)滑窗搜索以像素坐标为中心，只能获取整像素级光流。本文通过构建多尺度边缘直方图金字塔，并逐层搜索计算边缘光流，在一定程度上解决了这一问题，算法流程如图4所示。

由于边缘直方图仅有一维，这里采用一维高斯加权矢量替代式(1)的高斯卷积核进行边缘直方图金字塔的构建，第L层边缘直方图x坐标处的边缘数值可用L-1层边缘直方图表示为：

6hL-1(2x)+4hL-1(2x+1)+

hL-1(2x+2)]

(9)

图4 多尺度边缘光流算法流程图Fig.4 Flow chart of Multi-Scale Edge-Flow method

边缘直方图金字塔构建完成后，首先在最上层(k层)进行滑窗搜索，将得到的搜索结果变换至k-1层作为该层的搜索起点；随后，逐层重复上述过程直至获取第0层坐标t0；此时获取的光流v0=t0-q为与真实亚像素级光流最为接近的整像素级光流，直接对完整边缘直方图进行上采样会带来许多不必要的计算。因此这里首先对以t0为中心，半径为[-1,+1]区间内所有坐标位置处的边缘数值进行线性插值，随后在该区间内寻找满足式(10)的亚像素修正量Δt，最终得到亚像素级光流vs=t0+Δt-q。

(10)

3 仿真校验

为验证所提出的多尺度边缘光流特征提取与跟踪方法的有效性和可行性，基于嫦娥4号探测器LCAM获取的真实图像序列进行了仿真校验。仿真程序基于C++开发并部署在Linux环境的Robot Operation System中；仿真平台硬件配置为Intel(R) Core(TM) i5-8300@2.3 GHz CPU+8 GB RAM+GTX 750M GPU；为保证算法耗时比较的准确性，所有GPU加速功能在仿真中均未开启，全部运算均由CPU独立完成。

CE-4动力下降时序如图5所示，主要包括着陆准备、主减速、快速调整、垂直接近、悬停避障和缓速下降六个阶段。其中，着陆器在着陆准备段、主减速段和垂直接近段的飞行时间最长；在快速调整段和垂直下降段分别存在由持续姿态机动和快速水平机动引起的大尺度运动(大于10 pixel/s)[18](图5中双线框部分)。

图5 CE-4动力下降段降落时序Fig.5 Landing sequence of CE-4 power descent

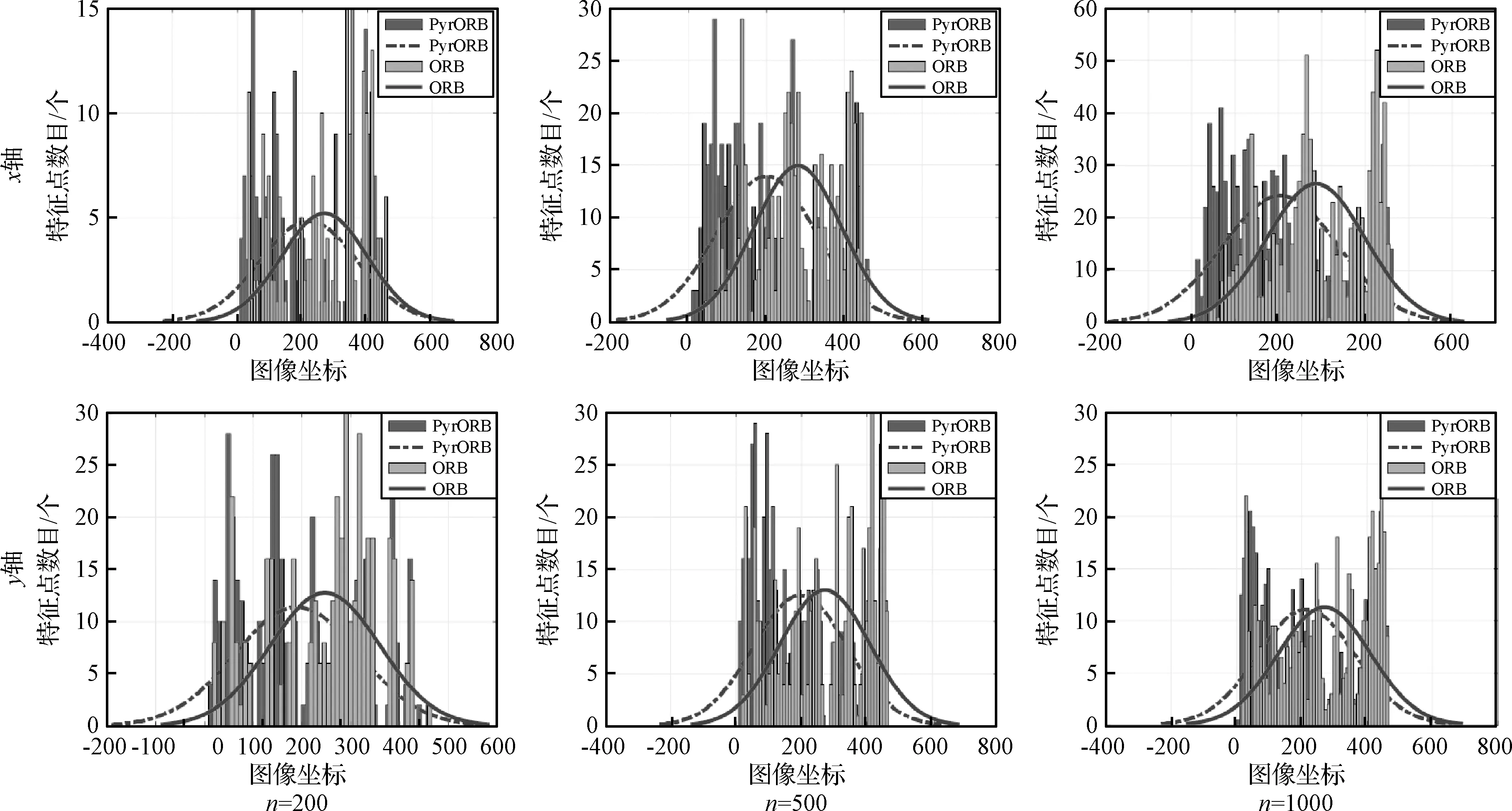
图6 M-ORB与ORB特征点坐标分布直方图对比Fig.6 Histogram of feature distribution between M-ORB and ORB

CE-4动力下降过程中所使用的LCAM的视场角为45.3°，焦距为8.5 mm，有效像素数为1024×1024，图像采集帧率为10 FPS。图7给出了所提出的M-ORB算法和传统ORB算法在不同特征点数目(依次为200、500和1000)下的两轴坐标分布直方图。可以看出，三种情况下M-ORB算法所提取特征点分布的均值和方差均小于传统ORB算法，特征点的空间分布更加均匀。

随后，进一步对M-ORB+BRIEF、M-ORB+KLT、M-ORB+EF及M-ORB+M-EF四种算法在真实场景下的性能进行了仿真校验和比较分析(由于特征提取部分均为M-ORB算法，为书写方便，下文以追踪部分算法名称代指)，各项算法仿真参数如表1所示。跟踪精度评估方面，在获得特征跟踪结果后，采用如式(11)所示绝对差值和(Sum of absolute difference，SAD)算法对每种跟踪算法的正确跟踪特征点数目进行重校验以保证评估指标的一致性，式中(xr,yr)和(xc,yc)为分别为特征点在前后帧图像中的像素坐标，k为窗口尺寸，通常取奇数。计算耗时评估方面，则采用相对计算耗时(特征跟踪耗时占总时间的比例)作为评估指标以避免随机性影响。

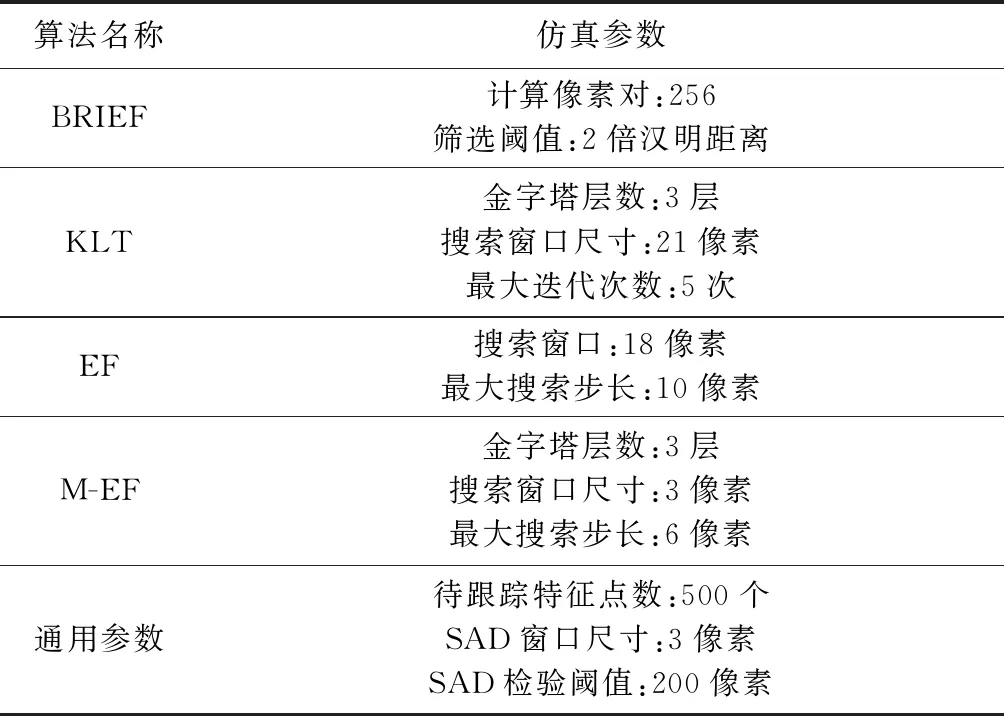
表1 各算法仿真参数设置Table 1 Simulation parameters for all tracking methods

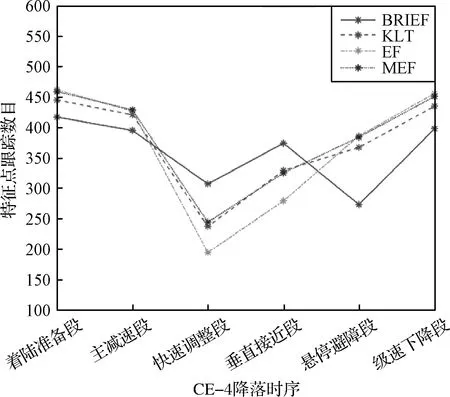
图7 CE-4动力下降各段不同跟踪算法平均跟踪特征点数目Fig.7 Average tracked feature numbers of different tracking methods during entire CE-4 power descent

图8 CE-4动力下降各段不同跟踪算法相对计算耗时Fig.8 Relative elapsed time of different tracking methods during entire CE-4 power descent

表2 CE-4动力下降各段平均跟踪特征点数目Table 2 Summary of average tracked feature numbers of different tracking methods during entire CE-4 power descent

表3 CE-4动力下降各段不同跟踪算法相对计算耗时Table 3 Summary of relative elapsed time of different tracking methods during entire CE-4 power descent

(11)

四种算法在动力下降各段的平均跟踪特征点数目和相对计算耗时分别如图7～8和表2～3所示。仿真结果表明，基于描述子的BRIEF算法在所有阶段的平均跟踪特征点数目变化幅度最小，对于大尺度运动的鲁棒性更好，但随之带来了较大的计算负担，相对计算耗时在13.86%左右。

三种基于光流的跟踪算法在较为平稳的降落阶段具有更高的平均跟踪特征点数目，其中EF及改进的M-EF算法略高于KLT算法。但当存在较大尺度运动的快速调整和垂直接近段，三种光流跟踪算法的平均跟踪特征点数目均出现不同程度下降，其中以EF算法最为严重。KLT及所提出的M-EF算法由于引入了多尺度策略，在一定程度上提高了大尺度运动下的特征跟踪稳定性，相比BRIEF算法下降在15%左右。

在相对计算耗时方面，三种光流跟踪算法均不超过BRIEF算法的50%，其中未采用多尺度策略的EF算法相对耗时仅为2.56%左右，采用多尺度策略的M-EF和KLT算法计算耗时则依次略有增加，分别在5.12%和6.83%左右。

4 结 论

基于描述子的传统视觉特征提取和跟踪方法存在耗时长、误匹配率高等问题，不能满足月面着陆器动力下降段自主导航的精度和鲁棒性要求。本文结合图像边缘直方图和图像金字塔策略，提出了一种多尺度边缘光流特征提取与跟踪方法、该方法在有效实现光流计算降维，提高计算效率的同时，改善了大尺度运动下特征跟踪的鲁棒性，将光流计算精度拓展至亚像素级。仿真结果表明，本方法计算耗时不超过传统描述子方法的50%；在非大尺度运动下具有最高的稳定跟踪特征点数目；大尺度运动下相比描述子方法下降不超过15%，优于原始EF算法，与同样采用多尺度策略的KLT算法基本持平。本方法在跟踪效率和稳定性方面取得了较好的平衡，是对传统方法的有效改进，具有一定的工程应用价值。