大型运载火箭加筋柱壳近似建模方法

王志祥，武泽平，王 婕，王 君，欧阳兴，张大鹏，雷勇军

(1. 国防科技大学空天科学学院，长沙 410073；2. 北京宇航系统工程研究所，北京 100076)

0 引 言

薄壁加筋柱壳结构以其较高的轴压、弯曲和扭转承载效率，广泛地应用于运载火箭及导弹舱段等航天结构中。作为运载火箭的主要承力部段，薄壁加筋柱壳轻量化设计可大幅提高运载能力和节约设计成本。对于轴压工况下的此类薄壁加筋柱壳结构，整体后屈曲失稳是其主要破坏模式，轴压极限承载能力是主要设计目标。后屈曲分析方法主要有非线性显式动力学方法和非线性隐式分析方法，相对Newton-Raphson法、Riks法等非线性隐式分析方法，显式动力学方法可以准确地模拟加筋柱壳的后屈曲行为，且算法收敛性能较好，但其计算耗时受模型复杂度，单元尺寸及数量等影响较大，这直接决定了加筋柱壳分析、优化效率。为满足我国大型运载火箭大幅提升的承载需求，主承力部段将大量采用整体加筋、框桁加强的薄壁壳体结构，其直径和承载性能将实现跨越式提升。对于在研的重型运载火箭，箭体直径达10米级，主承力舱段轴向载荷将达万吨级，大直径大载荷的结构特点将对薄壁加筋柱壳轻量化设计效率和精细程度提出更高要求，传统的以工程手册和设计经验为主，辅以有限元校核的设计方法将不再具有借鉴和参考意义，亟需发展一套高精度、快速的分析、优化方法来缩短薄壁加筋柱壳乃至整箭的研制周期。

为提高薄壁加筋柱壳屈曲/后屈曲分析、优化效率，国内外学者开展了大量研究。等效刚度法(Smeared stiffener method, SSM)因其具有较高的分析效率而广泛应用于薄壁加筋柱壳屈曲分析中[1]，其核心思想是基于解析法对筋条进行刚度等效，进而将薄壁加筋柱壳转化为薄壁柱壳结构。然而，加筋构型、边界条件以及载荷的复杂性极大地制约了SSM的适用性。代表体积元(Representative volume element, RVE)和渐近均匀化法(Asymptotic homogenization method, AHM)采用数值等效方法，相较解析法具有更高的精度和适用性，但其在大规模复杂结构的应用中求解效率较低。Cheng等[2]和Cai等[3]发展了AHM法，提出了一种新的渐近均匀化数值实现方法(Numerical implementation of asymptotic homogenization, NIAH)，极大地提高了分析效率。Hao等[4]采用NIAH方法建立了开口加筋柱壳的混合等效模型。针对多级加筋柱壳设计问题，Wang等[5]采用NIAH法对次筋条进行刚度等效，建立了多级加筋柱壳的混合等效模型，有效地提高了分析优化效率。在上述工作中，加筋柱壳的筋条截面形状相对简单，由于应用NIAH方法时需首先采用AHM方法对周期性单胞结构进行刚度等效，对筋条刚度的高精度等效确保了NIAH方法的分析精度，而在加强框、桁截面形状多样的大直径大载荷薄壁柱壳后屈曲分析应用上，NIAH方法仍存在刚度等效精度和算法适用性等方面的挑战。

针对上述问题，可将复杂耗时的结构分析当成黑箱处理，通过数值分析方法揭示输入和输出间的非线性映射关系，进而实现对复杂结构的高效分析和优化。近似模型(Approximation Model)以其具备反映真实模型输入和输出间的非线性关系和快速预测等优点受到广泛关注并成功应用于飞行器结构和气动分析与优化设计中[6-8]。Queipo等[9]指出，近似模型及基于近似模型的近似优化方法对提高现代航空航天系统的性能，降低其设计成本具有重要意义。目前广泛使用的近似模型有Kriging[10]近似模型、径向基函数[11-12](Radial basis function, RBF)近似模型、椭圆基函数[13](Elliptical basis function, EBF)近似模型和支持向量回归[14](Support vector regression, SVR)近似模型。RBF近似模型以其非线性泛化能力强、训练样本点处预测误差为零等优势受到众多研究者关注。

在实际应用中，RBF近似模型预测精度严重依赖于基函数中形状参数的取值，因此形状参数的确定成为研究RBF近似模型的难点和热点[15]。Nakayama等[16]针对样本点均匀分布情况，提出了一种形状参数的直接确定方法。Kitayama等[17]指出该方法的不足，并针对样本点非均匀分布情况对该方法进行了改进。但上述两种方法仅通过样本点在空间中的分布确定形状参数，忽略了模型响应对形状参数的影响。Esmaeilbeigi等[18]采用遗传算法确定形状参数最优取值，并应用于微分方程的求解。Mongillo[12]基于交叉验证的方法对径向基函数的选取和形状参数的确定开展研究。但针对复杂高维系统进行近似建模时，往往需要大量训练样本点以建立满足精度需求的近似模型，前述工作中的形状参数优化问题将包含与训练样本点数量相当的独立优化变量，这极大地增加了问题的复杂度。为简化形状参数优化问题复杂度，姚雯[19]基于相邻样本点具有相似空间分布特性和模型响应非线性分布特性的假设，提出了形状参数的分簇优化方法，进而实现近似精度和建模效率的折中。针对该问题，Wu等[20]提出了基于样本点局部密度的形状参数快速确定方法，有效地解决了形状参数优化复杂度随样本规模急剧攀升的难题。

RBF近似模型在近似高阶非线性模型方面具有优越的性能，但其在近似非线性程度较低或线性模型时，泛化能力相对不足。为进一步增强RBF近似模型对线性模型的泛化能力，Gutmann[21]提出了引入线性项的增广径向基函数近似模型，并成功应用于全局近似优化方法中[22]。但从公开文献来看，目前针对ARBF的近似建模方法研究较少，且鲜有文献将ARBF近似模型运用到薄壁加筋柱壳的后屈曲分析与优化中。

本文针对ARBF近似模型的建模方法开展研究，并探索ARBF近似建模方法在大直径大载荷、框桁加强的薄壁柱壳后屈曲分析和优化方面的应用潜力。首先，给出了ARBF近似模型的数学模型；然后，基于样本点局部密度给出了基准形状参数快速确定方法，根据模型响应特点，引入了缩放系数对形状参数进行自适应调整；进而，基于矩估计理论，详细推导了求解缩放系数的适应度函数，将确定形状参数优化问题转化为求解缩放系数的优化问题，并采用多起点并行优化算法求解该优化问题；最后，采用典型数值算例和大直径大载荷加筋柱壳结构对本文方法进行验证，与其他典型近似模型的对比结果均表明了本文方法的有效性和工程适用性。本文所提的基于矩估计的ARBF高精度近似建模方法及相关结论可为提高我国大型运载火箭薄壁加筋柱壳结构设计效率提供工程参考。

1 增广径向基函数近似模型

不失一般性，单位立方体空间Ω=[0, 1]m中，对于给定的一组训练样本集S

S={[xi,yi]|xi∈Rm,yi∈R,|i=1,2,…,N}

(1)

其中，Rm为m维设计空间，xi为第i个样本点，yi为第i个样本点对应真实模型的输出，N为训练样本集S中样本点的个数。ARBF数学表达式为

(2)

其中，x为输入值，φi为对应第i个样本点的基函数，ωi为第i个基函数的权值，λj为多项式系数，gj为多项式g的第j项。通常情况下多项式g仅考虑常数项和线性项，表达式为

(3)

式中：x(k)表示向量x的第k维分量。

将训练样本点[xi|yi|]代入式(2)，得到如式(4)所示的线性方程组。

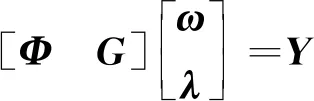
(4)

由于训练样本集S中的样本点互不相同，因此G为列满秩矩阵，且当训练样本点数量N>m+1时，必存在非零向量ω使得GTω=0成立，即

(5)

联立式(4)和式(5)，进而得到如式(6)所示的关于基函数权重系数ω和线性回归系数λ的线性方程组。

(6)

(7)

(8)

式中：ci为第i个Gauss基函数的形状参数，决定了第i个样本点对周围空间的影响衰减程度。Gauss基函数随形状参数的衰减程度如图1所示，形状参数ci越小，基函数衰减越快，其相应样本点对周围空间的影响范围越小，反之则越大。

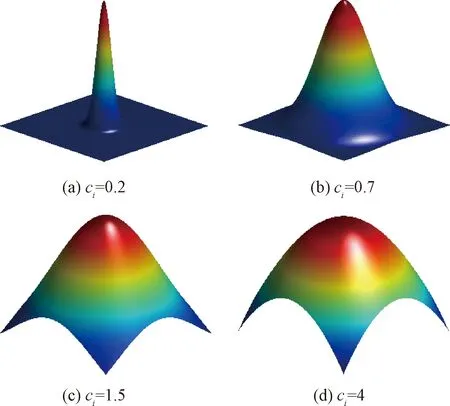
图1 不同形状参数下Gauss基函数Fig.1 Gaussian kernel functions with different shape parameters plotted on the same domain

图2 形状参数不同取值下近似模型Fig.2 The approximation models under different shape parameters

以式(9)所示的一维函数f(x)为例，进一步分析形状参数的取值对近似模型近似能力的影响规律。以[0,1]区间内均匀分布的10个采样点为训练样本点，采用ARBF对f(x)进行近似建模。

f(x)=x2-sin(4πx2)

(9)

2 形状参数矩估计法

2.1 基于局部密度函数的形状参数确定方法

如前所述，Gauss基函数形状参数对近似模型近似精度具有显著影响。考虑到相邻样本点应具有相似的真实模型响应特性，为了确定形状参数的较优取值，需首先针对训练样本点在空间中的分布情况开展研究。

文献[20]提出了样本点局部密度函数用于衡量样本点在空间中分布的疏密程度，其具体表达式为

(10)

其中，σ为样本点对设计空间中局部密度的贡献程度，可通过下式确定[20]

(11)

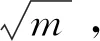
(12)

图3和图4分别表示一维空间和二维空间中样本点局部密度分布。由图3～4可知，在样本点密集区域，样本点密度函数值较高；在样本点稀疏区域，样本点密度函数值较低。

基于Gauss基函数随形状参数的衰减特点，为充分利用样本点信息，应增大稀疏区域样本点对周围空间的影响范围，减小密集区域样本点对周围空间的影响范围。因此，令样本点影响范围与样本点局部密度成反比[23]，即

(13)

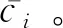
(14)

(15)

最优形状参数不仅受训练样本点空间分布的影响，还在一定程度上取决于真实模型的响应特性，因此，在保持各个形状参数比值不变的基础上，需将形状参数按式(16)进行自适应缩放。

(16)

式中：ε为缩放系数。

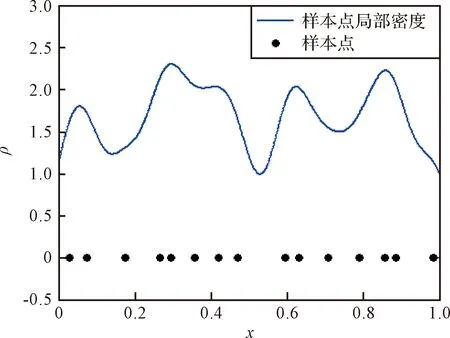
图3 一维空间样本点局部密度曲线Fig.3 Curve plot for local density of the sampling points in one-dimension space

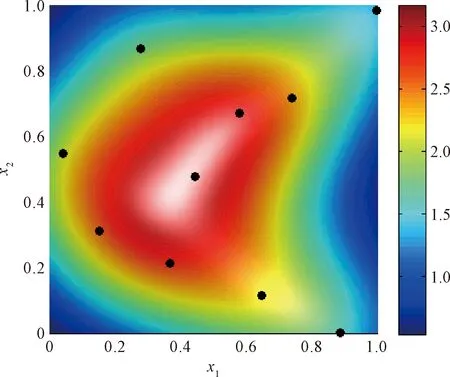
图4 二维空间中样本点局部密度等高线图Fig.4 Contour plot for local density of the sampling points in two-dimension space

2.2 基于矩估计的缩放系数ε确定方法

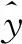
(17)

(18)

基于训练样本点和近似模型获得的各阶矩都是对真实模型的近似，因此，合适的缩放系数ε将使得两种方式获得的各阶矩相同，即

(19)

通过求解式(19)，即可求得最优缩放系数ε，但一般很难使得如式(19)所示的各阶矩严格相等。因此，可通过求解如式(20)所示的最小化问题获得合适的缩放系数，进而通过式(16)获得合适的形状参数。

εopt=argminF(ε)

(20)

式中：

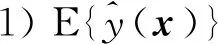
(21)

令

(22)

其中，

(23)

(24)

其中，Φ(x,μ,σ)表示均值为μ方差为σ的正态分布函数在x处的累计值。同时，为后文表述方便，记

Ψ(x,μ)=Φ(1,x,μ)-Φ(0,x,μ)

(25)

(26)

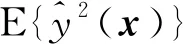
(27)

(28)

第一项E1可进一步化简为

(29)

其中，

(30)

进而，得E1的解析表达式为

(31)

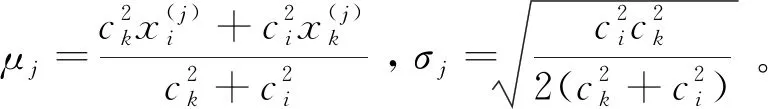
对于式(27)中第二项，E2可进一步化简为

(32)

其中，

(33)

(34)

将式(33)～(34)代入式(32)，得E2的解析表达式为

(35)

对于式(27)中第三项，E3可进一步化简为

(36)

式中：

(37)

基于式(23)～(24)及式(37)，可得E3的解析表达式为

(38)

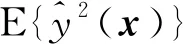
(39)

至此，基于矩估计方法已将确定形状参数的复杂域优化问题转化为确定缩放系数的优化问题，大幅降低了形状参数优化问题的复杂度。

图5 ARBF矩估计近似建模流程图Fig.5 Flowchart of the construction for the ARBF approximation model based on moment estimation

图5为本文提出的ARBF矩估计近似建模方法流程图。建立高精度近似模型的核心问题包括两部分，训练样本点的选取和缩放系数的优化。训练样本点的空间均布性影响近似模型的全局近似精度。优化算法的选取一定程度上影响建模的效率和精度，针对如式(20)所示的优化问题，本文采用多起点并行优化算法[24]进行求解，进一步提高优化搜索效率和精度。值得说明的是，缩放系数的最优取值一定程度上取决于真实模型的响应特性，基于本文研究经验，可首先通过试凑法确定缩放系数取值范围，然后基于优化算法进行优化求解。在本文数值算例及工程应用研究中，缩放系数取值范围均为[0.1,10]。

3 算例验证

为了验证本文所提近似建模方法的有效性，本节分别采用本文方法、Kitayama方法[17]、RBF[12]、EBF[13]以及Kriging[10]建立近似模型，并对各近似模型的全局和局部近似能力进行评估。近似模型精度评估准则如表1所示，其中R2和ERMSE表征近似模型的全局近似能力，ERMAE表征近似模型的局部近似能力。

3.1 数值算例

本节选取4个经典的非线性多峰值数值函数[25-26]对本文方法进行测试，并与其他四种近似模型建模方法进行对比。数值函数数学表达式及测试维数如表2所示。首先基于优化拉丁超立方试验设计方法(Optimal Latin hypercube design, OLHD)生成在设计空间内均匀分布的样本点；然后基于该样本点分别采用上述五种建模方法建立各数值函数的近似模型；最后采用蒙特卡洛方法生成10000个样本点对各近似模型近似能力进行评估。文献[6]基于OLHD生成30倍设计变量数的初始样本点用于训练近似模型，近似模型获得了较高的近似精度。为测试本文方法构建的近似模型在样本点分布稀疏下的泛化能力，各测试函数的训练样本点数量如表2所示。为减小随机误差对评估结果的影响，上述过程独立重复10次。

表1 近似模型精度评估准则Table 1 Error metrics of approximation model

不同近似模型对表2中4个测试函数的近似精度盒型图分别如图6～图9所示。由于Kitayama方法是通过样本点的空间距离直接确定形状参数，不能有效地近似非线性多峰值问题，因此相对其他四种模型，Kitayama方法确定的近似模型精度相对偏低。图6所示为低维测试函数近似精度对比盒型图，本文方法与RBF和EBF模型全局和局部近似精度均相当，且均高于Kriging近似模型。图7～图9为高维测试函数近似精度对比盒型图，由图7～图9可知，本文方法全局和局部近似精度均显著高于其他四种近似模型，尤其对于12维GN函数，在训练样本点数量相对较少的情况下，其他四种近似模型的近似能力严重不足，本文方法仍能获得较高的近似精度。

注意到图6～图9近似精度盒型图中存在异常值，这主要是训练、测试样本点空间分布具有一定的随机性所致，且本文方法异常值对应的近似精度相比其他典型近似建模方法(Kitayama、RBF、EBF、Kriging)更高。

表2 数值测试函数Table 2 Numerical test functions

图6 不同近似模型对Rosenbrock函数近似精度盒型图Fig.6 Boxplots of approximation accuracy for the Rosenbrock function

图7 不同近似模型对Ellipsoid函数近似精度盒型图Fig.7 Boxplots of approximation accuracy for the Ellipsoid function

图8 不同近似模型对Griewank函数近似精度盒型图Fig.8 Boxplots of approximation accuracy for the Griewank function

图9 不同近似模型对16-Variable函数近似精度盒型图Fig.9 Boxplots of approximation accuracy for the 16-Variable function

综上所述，在设计空间中训练样本点分布较为稀疏时，相对其他典型近似模型建模方法，本文方法能以更高精度逼近高维多峰值非线性函数，且由图6～图9中盒型图数据分布可知，与其他方法相比，本文方法评估结果的数据分布相对更集中，说明本文方法受训练样本点的分布影响较小，算法鲁棒性更高。特别地，在训练样本点数量相对设计变量数较少(相比于文献[6])的情况下，本文方法对低维和高维测试函数均具有较高的近似精度，同时，经大量分析可知，问题的高度非线性及多峰值特性相比问题的维数更影响近似精度。

3.2 工程应用

作为典型的框桁加强薄壁加筋柱壳结构，蒙皮桁条结构以其较高的轴压承载性能广泛应用于运载火箭结构设计中。蒙皮桁条结构主要由端框、中间框、桁条和蒙皮组成。蒙皮内侧沿高度方向布置4个“Ω”形截面中间框，端部各布置一个“L”形端框，同时，蒙皮外侧沿环向均匀布置“工”形截面竖向桁条。中间框布局形式及参数如图10(a)所示，端框、中间框及桁条的截面形式及参数如图10(b)所示。各构件截面尺寸及中间框布局参数取值范围如表3所示。

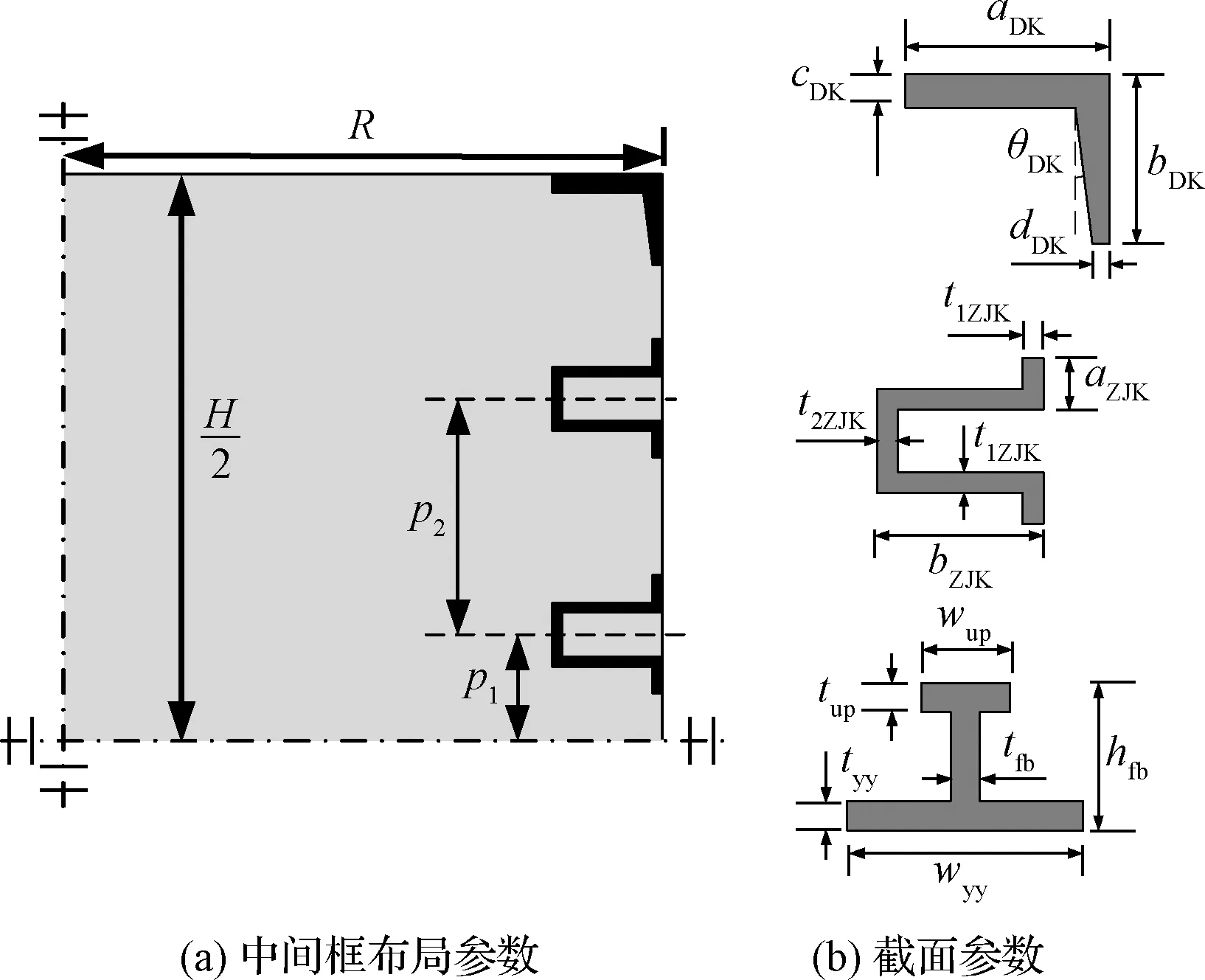
图10 蒙皮桁条结构设计参数Fig.10 Design variables of the cylindrical stiffened shells

表3 设计变量取值范围Table 3 Range of design variables

蒙皮桁条结构主要通过桁条来提高结构轴压承载性能，环向中间框通过抵抗桁条径向弯曲变形进一步提高桁条承载能力，蒙皮的主要作用则是保持结构几何形状及支撑桁条。在相对较小的载荷下蒙皮即发生局部失稳和局部进入塑性，但结构仍能继续承载，直至结构发生整体压溃破坏，因此该结构的极限承载能力由结构整体稳定性和后屈曲状态决定。

本文采用显式动力学方法对蒙皮桁条结构进行后屈曲分析，其轴压位移-载荷曲线及对应的线性前屈曲-非线性后屈曲-直至压溃破坏时结构径向变形云图如图11所示，轴压位移-载荷曲线最高点对应的轴压载荷为极限载荷，即表示结构极限承载能力。但在采用传统优化算法对此大规模复杂结构进行优化设计时，需反复调用显式动力学方法计算，分析耗时将急剧飙升。为提高分析和设计效率，缩短设计周期，需采用近似建模技术高效、高精度逼近模型设计参数与极限承载能力间的复杂映射关系。

空间均布性及填充性高的样本点能够以更大的概率捕获近似对象的特征信息，提高近似模型的精度。为尽可能多地捕获模型特征信息和充分利用样本点信息，提高计算效率，本文首先基于OLHD方法在如表3所示的19维设计空间中生成2400个样本点，并利用并行计算资源计算对应样本点的结构质量和极限载荷；然后采用聚类算法[29]随机选取在空间中均匀分布的300个样本点作为训练样本点构建近似模型，其余2100个样本点作为测试样本点评估近似模型全局和局部近似精度。为减小随机过程对评估结果的影响，上述第二步过程独立重复10次。

图11 加筋柱壳轴压位移-载荷曲线及变形云图(5倍放大效果)Fig.11 Load vs end-shortening curve and deformation patterns (scaling factor 5) of cylindrical stiffened shells

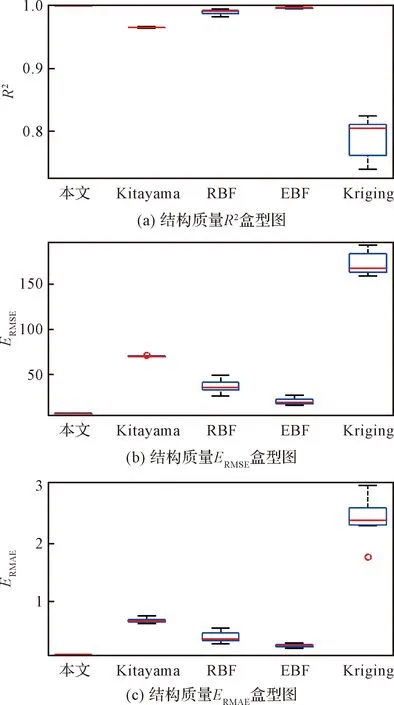
图12 不同近似模型对结构质量近似精度盒型图Fig.12 Boxplots of approximation accuracy for the structural mass of cylindrical stiffened shells

图13 不同近似模型对极限载荷近似精度盒型图Fig.13 Boxplots of approximation accuracy for the collapse load of cylindrical stiffened shells

针对上述10组不同的训练和测试样本点，分别基于本文方法、Kitayama方法、RBF、EBF以及Kriging建立近似模型并评估近似精度，不同近似模型针对蒙皮桁条结构质量和极限载荷的近似精度盒型图如图12～图13所示。对于结构质量，在全局和局部近似精度方面，本文方法近似精度均最高，EBF近似模型次之，Kriging近似模型精度相对最低。对于极限载荷，在全局近似精度和局部近似精度方面，本文方法与EBF近似模型相当，但高于Kitayama方法和RBF近似模型，显著高于Kriging近似模型。相对极限载荷，结构质量与设计变量间的非线性关系更易被捕获。同时，从盒型图数据分布可知，本文方法建立的近似模型的精度评估数据仍相对更集中，算法鲁棒性更高。

4 结 论

本文以大型运载火箭薄壁加筋柱壳结构优化设计为研究背景，提出了基于矩估计的增广径向基函数近似建模方法。主要工作和结论可总结如下：

1)结合增广径向基函数数学模型，分析了形状参数对近似模型泛化能力的影响，过小的形状参数使得近似模型泛化能力不足，过大的形状参数使得系数矩阵病态，出现“龙格现象”。

2)综合考虑样本点空间分布及真实模型响应特性对形状参数的影响，引入样本点局部密度和形状参数缩放系数，并基于矩估计方法，成功将确定形状参数的复杂域优化问题转化为确定缩放系数的优化问题，显著降低了形状参数优化问题的复杂性。

3)典型数值算例及工程应用对比研究表明：相对其他典型近似建模方法，本文方法能够以更高的全局和局部近似精度泛化模型设计变量与模型响应间的复杂映射关系，且算法鲁棒性更高，有利于提高薄壁加筋柱壳后屈曲分析和优化效率。

综上所述，本文所提的近似建模方法可为提高我国大型运载火箭薄壁加筋柱壳设计效率提供工程参考。