四维超混沌射频隐身跳频通信设计方法
杨宇晓,汪德鑫,黄 琪
(南京航空航天大学航天学院,南京 210016)
0 引 言
近年来,随着传感器元器件水平的飞速发展,无源探测系统(无源态势感知、电子情报系统ELINT、信号情报系统SIGINT等)对主动辐射源的探测能力已大大提高,对航天器的在轨安全构成了严重威胁[1-2]。为提高航天器的在轨生存能力,航天器搭载的主动辐射源必须进行射频隐身设计[3-5]。
信号最大不确定性设计是射频隐身理论的重要策略,利用信号频域、时域和空间域参数的不确定设计,增加对抗方侦察设备的预估难度,提高信号的抗分选和抗截获能力。通信信号频域特征的不确定设计是国内外学者研究的热点,研究成果主要集中在频率序列设计,1974年,Lempel和Greenberger建立了跳频序列最大周期汉明自相关理论界,称之为Lempel-Greenbeger界[6],并基于有限域的m序列构造了满足该理论界的最优跳频序列。在此基础上,Peng等[7]提出了构造具有最优最大汉明相关值跳频序列的一般化构造方法。混沌系统具有强随机特性,以混沌理论为基础的跳频序列设计也得到了研究者的广泛关注,Liu等[8]提出一种新的基于非稳态Logistic映射的混沌序列发生器,提高了系统的抗截获性能。Georges[9]提出了一种基于差分混沌移位键控的OFDM调制方式,采用重复的混沌参考信号发送扩频信息,提高频谱效率的同时减少了能量消耗。
混沌序列由于其不可预测和初值敏感特性,具有复杂的非线性动力学特征和不确定性[10],其在通信频率特征的不确定设计中已得到了广泛应用。然而,随着研究工作的不断深入,也出现了一些亟待解决的挑战。具体表现在:
1)随着高性能计算的发展,Logistic等低维混沌系统由于维数较低、密钥参数较少、复杂度有限等缺点,难以抵御高性能计算机和高级计算算法的攻击,文献[11-12]等已给出了低维混沌系统被破译的实例。
2)由于实现混沌系统的计算机、数字电路等计算平台的运算精度难以无限提高。在有限精度条件下,混沌系统的连续状态被离散化,系统混沌特性退化,导致输出序列出现短周期现象,影响了混沌序列的不确定性能。
综上所述,为解决传统低维混沌系统的复杂度有限和短周期现象,本文提出了一种基于扰动的四维超混沌系统构建方法,将低维混沌扩展至四维系统,大大提高了系统的解空间,增加了系统复杂度,同时,引入扰动设计,打破原有系统状态映射中的闭合状态集,从而消除短周期现象。在此基础上,利用四维超混沌系统对跳频信号的频率特征和周期特征进行联合设计,提出了基于四维超混沌系统的跳频通信不确定设计方法。仿真结果表明:根据本文所提方法设计产生的跳频信号具有较好的抗分选能力,其截获概率远低于常规跳频信号,有效提高了信号射频隐身能力。
1 四维超混沌构建
超混沌系统具有复杂的相空间特征,其复杂程度较传统混沌系统显著提高[13],可生成具有优异复杂度性能的跳频图案,降低破译风险。
1.1 四维超混沌系统构建
本文以经典的Lorenz三维混沌系统[14]为基础,引入反馈控制机制和周期性扰动措施,构建四维超混沌系统。Lorenz混沌系统方程如下式(1)所示:

(1)
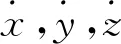
本文在Lorenz混沌系统基础上,引入第四维控制器W对原系统进行反馈控制。控制器W由原系统控制器X,Y和Z进行联合控制,W控制器的输出信号反馈至原系统控制器X中,形成系统内部的闭环反馈。四维系统方程如式(2)所示:

(2)

为解决传统低维混沌系统的短周期现象,本文在上述四维系统中引入周期性扰动措施,使系统跳出系统状态的闭合状态集,解决有限精度带来的短周期现象。由文献[15]可知,扰动信号需满足以下三个原则:
1)均匀性原则。扰动信号幅值应在一定区间内分布均匀;
2)高信噪比原则。原信号与扰动信号信噪比应远大于1,扰动信号对原信号幅值不产生明显影响,扰动信噪比Ssnr如下式(3)所示:
(3)
式中:Vc是原信号的最大幅值,Vr为扰动信号的最大幅度。
3)短间隔原则。扰动信号的时间间隔应远小于系统的运行时间。
依据以上设计原则,本文在第四维控制器W后端增加扰动信号rs,扰动信号由扰动因子r和符号函数sgn生成,并最终周期性耦合至控制器Y中。扰动信号rs如下式(4)所示:
rs=h·sgn(w)
(4)
式中:h为扰动信号幅度,用以满足扰动信号设计的高信噪比原则;符号函数sgn(w)作为扰动信号驱动,通过控制器W的取值来保证其均匀性。
由上述可知,引入扰动设计的四维超混沌系统方程如下式(5)所示:
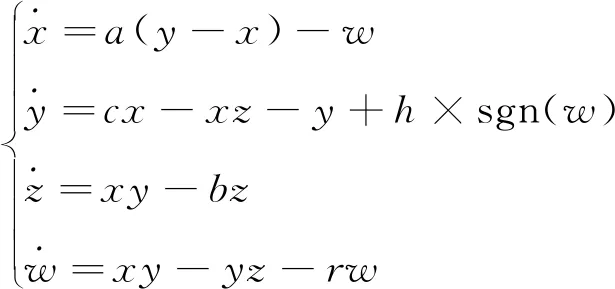
(5)

四维超混沌系统的组成框图如图1所示。

图1 四维超混沌系统组成框图Fig.1 Block diagram of four-dimensional hyperchaotic system
1.2 超混沌参数设计
针对1.1节构建的四维系统,通过系统参数设置,可以实现系统处于超混沌状态。超混沌系统的状态判定主要利用Lyapunov指数法,对于四维系统,Lyapunov指数与系统状态之间的对应关系[16]为:
1)若系统Lyapunov指数存在一个零值和三个负值,则处于周期状态;
2)若系统Lyapunov指数存在一个正值,一个零值和两个负值,则处于混沌状态;
3)若系统Lyapunov指数存在两个正值,一个零值和一个负值,则处于超混沌状态。
若四维离散混沌系统迭代方程为:
(6)
则(xn+δxn,yn+δyn,zn+δzn,wn+δwn)点状态,由式(7)计算可得:

(7)
(δxn,δyn,δzn,δwn)可转换为:
(8)
式中:Jn-1,Jn-2,……,J0为n-1,n-2,……,0阶雅克比行列式。
则四维系统的Lyapunov指数λ1,λ2,λ3和λ4为:
(9)
通过对系统控制参数a,b,c,h和扰动因子r进行设置,可以实现四维系统的超混沌状态。控制参数a,b,c按照Lorenz混沌系统进行设置[14],a=10,b=8/3,c=28。考虑到扰动信号不能对原信号幅值产生明显影响,且扰动间隔应尽可能短,设置扰动信号幅值为0.01,扰动周期Nr=1000,则扰动信号幅度h定义为:
(10)
式中:n为系统迭代次数,f1(x,y)为取余函数。
扰动因子r是第四维控制器的重要参数,对四维系统的混沌特性具有显著影响,本节根据Lyapunov指数计算方法,分析了不同扰动因子r值条件下的Lyapunov指数分布情况。
由图2(a)λ1,λ2,λ3和λ4仿真数据可知,在r∈[0, 4]范围内,λ4<0。图2(b)的仿真局部数据则清晰反映了另外三个Lyapunov指数λ1,λ2和λ3的取值。根据Lyapunov指数与系统状态之间的对应关系,四维系统状态可分为三个部分:当r∈[0, 1.52]时,系统处于超混沌状态;当r∈(1.52, 3.18]时,系统处于周期状态;当r∈(3.18, 4.00]时,系统处于混沌状态。针对三种系统状态,本节进一步对Lyapunov指数的具体数值进行了详细分析,分析结果如表1所示。
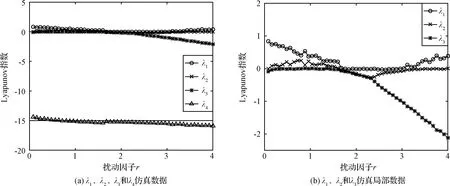
图2 不同扰动因子条件下的Lyapunov指数Fig.2 Lyapunov exponent under different disturbance factors
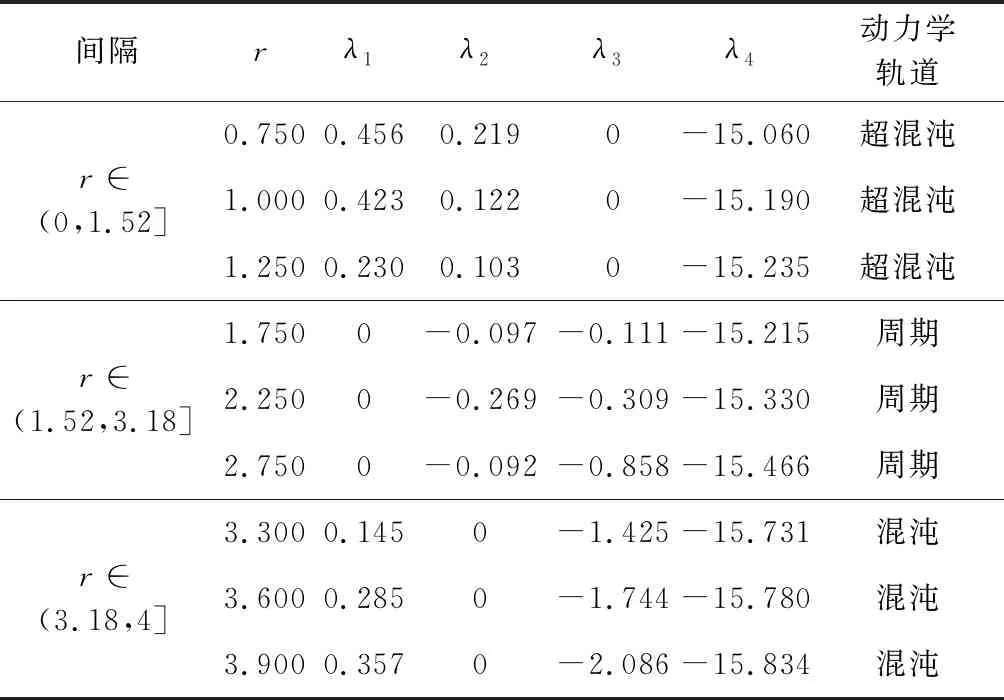
表1 四维超混沌系统Lyapunov指数Table 1 Lyapunov exponent of four-dimensional hyperchaotic system
1.3 复杂度评估
序列的复杂度可以采用近似熵[17]来进行度量,其思想是检测序列中新序列的产生概率,近似熵越大,序列的复杂度越高。若已知N维序列x(i),近似熵的计算方法如下:
1)将序列x(i)重构为m维向量α(i):
α(i)=[x(i),x(i+1),…,x(i+m-1)]
(11)
式中:i=1,2,…,N-m+1。
2)将α(i)与α(j)的对应元素最大差值记作d[α(i),α(j)],则:

(12)
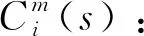
(13)

(14)
5)则序列的近似熵E(m,s,N)可定义为:
E(m,s,N)=Φm(s)-Φm+1(s),m≥2
(15)
1.4 周期性评估
为计算超混沌系统的周期,本节提出了一种序列周期快速搜索算法,算法实现步骤如下:
1)若混沌系统初值为{x0,y0,z0,w0},按照混沌系统方程迭代生成混沌序列;
2)设置迭代步进长度n和当前比较序列{xk,yk,zk,wk},其中k=n;
3)从第k+i次迭代开始,分别判断xk+i=xk,yk+i=yk,zk+i=zk,wk+i=wk是否成立,其中i=1,2,…,n;
4)若对于i,满足xk+i=xk,yk+i=yk,zk+i=zk,wk+i=wk条件,则记录周期T为i,并更新当前比较序列为{xk+i,yk+i,zk+i,wk+i},重复步骤3);
5)若对所有i=1,2,…,n,均不满足xk+i=xk,yk+i=yk,zk+i=zk,wk+i=wk条件,则当前序列设为{xk+n,yk+n,zk+n,wk+n},重复步骤3);
6)判断多次记录的T值是否相等,若相等则系统周期为T,否则不存在周期。
序列周期快速搜索算法流程图如图3所示:

图3 序列周期快速搜索算法流程图Fig.3 Flowchart of sequence period fast search algorithm
2 基于四维超混沌系统的跳频通信系统
传统跳频通信系统主要通过频率特征的不确定性设计提高跳频信号的抗截获性能,但传统跳频系统的跳频周期多为固定值,对抗侦察方仍可通过跳频频率集、跳频速率等参数估计,实现信号分选识别。本文利用四维超混沌系统,将跳频系统的跳频频率和跳频周期作为优化对象,提出了一种基于四维超混沌系统的跳频频率和跳频周期联合设计方法。
2.1 四维超混沌系列量化
由1.1节构建的四维超混沌系统可以产生具有强随机特性的实值序列,为利用超混沌序列生成跳频图案,首先需要将超混沌实值序列进行量化处理,分别生成频率编号序列和周期编号序列。
量化过程应重点考虑四维超混沌序列的动力学特性不受影响,因此,量化方法的选择至关重要。本文采用扩大取模法对超混沌序列进行量化处理,该方法首先去除实值序列整数部分,并将其小数部分扩大10n倍,进而根据量化级数进行取模运算,量化后序列q如式(16)所示:
q=f1(f2((|xi-f2(xi)|×10n)),K)+1
(16)
式中:xi,i=0,1,2,…为超混沌实值序列,K为量化级数,n为扩大级数,f1(x,y)为取余函数,f2(x)为向下取整函数。
2.2 哈希映射
经扩大取模法[18]量化处理后的整数序列为频率编号序列或周期编号序列,编号序列通过哈希映射表生成跳频图案对跳频系统的频率特征和周期特征进行控制。因此,需要建立编号序列与跳频图案间的哈希映射关系。
本文参考美国Link16数据链的跳频图案指标[19],构建具有48种跳频频率,最小跳频间隔为3MHz的跳频频率哈希映射表,频率编号与跳频频率映射关系如表2所示。

表2 跳频频率哈希映射表Table 2 Table of hopping frequency hash map
考虑到实际应用场景中的计算平台性能,本文构建具有8种跳频周期的哈希映射表,周期编号与跳频周期映射关系如表3所示。
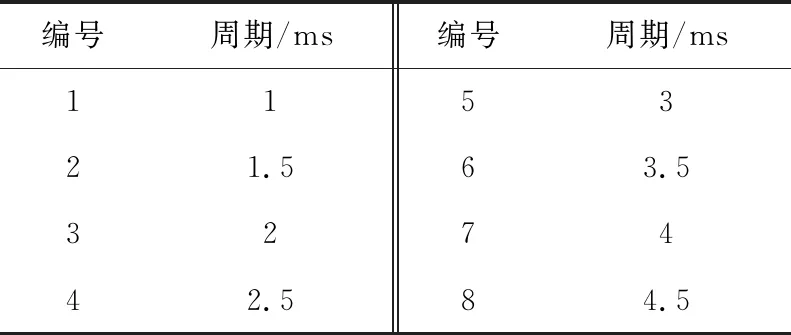
表3 跳频周期哈希映射表Table 3 Table of hopping period hash map
2.3 跳频频率和跳频周期联合设计
根据1.1节构建的四维超混沌系统,生成两组超混沌实值序列xk和yk,将这两组实值序列分别经过扩大取模量化处理后,生成频率编号序列和周期编号序列,进而按照2.2节中表2和表3所示的哈希映射表,产生跳频频率序列和跳频周期序列,实现对跳频信号跳频频率和跳频周期的联合设计。联合设计流程图如图4所示。

图4 跳频频率和跳频周期联合设计流程图Fig.4 Joint design flowchart of hopping frequency and hopping period
3 仿真结果与分析
3.1 四维超混沌系统仿真
为验证四维超混沌系统的有效性,本节将该系统与Logistic、Lorenz混沌系统进行了复杂度和周期性的对比仿真。
根据1.2节分析,四维超混沌系统初值为:x0=10,y0=10,z0=10,w0=10。控制参数设置为:a=10,b=8/3,c=28,h=0.01,r=0.75。Lorenz混沌系统初值为:x0=10,y0=10,z0=10。控制参数设置为:a=10,b=8/3,c=28。Logistic混沌系统初值为:x0=0.3,控制参数设置为:μ=4。
仿真1:复杂度比较
根据1.3节内容,本节以近似熵为复杂度的衡量指标,分别计算四维超混沌系统与Logistic、Lorenz混沌系统输出序列的近似熵。相似容限s参考文献[20],设置为序列标准差的1/10,重构向量维数m分别为2和3,经100次蒙特卡洛实验,三种系统输出序列的近似熵如图1所示。

图5 近似熵仿真结果对比Fig.5 Comparison of approximate entropy simulation results
对图5近似熵仿真数据进行平均处理,获得三种系统的近似熵均值,如表4所示。

表4 三种系统近似熵均值Table 4 Approximate entropy of three systems
由图5和表4仿真数据可知,四维超混沌系统近似熵最大,输出序列复杂度最高;Lorenz系统复杂度低于四维超混沌系统,Logistic系统近似熵最小,序列复杂度最低。
仿真2周期性比较
本文所提四维超混沌系统通过引入周期性扰动措施,使超混沌系统跳出系统的闭合状态集,解决短周期现象。为验证所提方法的有效性,本节采用1.4节的周期快速搜索算法,分别计算四维超混沌系统与Lorenz混沌系统的周期。
四维超混沌系统与Lorenz混沌系统的设置参数与前文相同,在有限精度分别为P=8和P=9时,利用周期搜索算法各计算10组T值,仿真结果如图6所示。
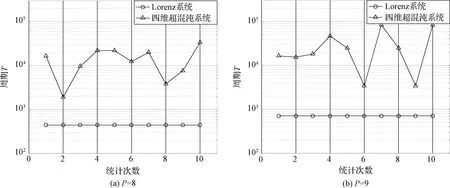
图6 周期搜索结果Fig.6 Results of period search
由图6仿真数据可知,Lorenz系统在两种有限精度条件下,输出序列均具有固定周期T,具有显著的短周期特征。而本文所提四维超混沌系统在相同的有限精度条件下,计算得到的输出序列T值均不相同,系统的不具有周期性。因此,四维超混沌系统有效消除了系统的短周期现象。
3.2 基于四维超混沌的跳频通信系统仿真
跳频系统的射频隐身性能可以用截获概率[20]来进行度量,截获概率越低,射频隐身性能越好。为验证基于四维超混沌的跳频通信系统的射频隐身性能,本节对该系统与常规跳频系统的截获概率进行对比仿真。
文献[21]给出了单个时间片内每个传感器的截获概率Ψ的计算公式:
Ψ≈M(2Pi/PI)CoDI(TOT/TI)(NF/FI)
(17)
式中:M为主瓣3 dB波束覆盖面积,Pi为截获接收机收到的功率,PI为截获接收机检测门限,DI为截获接收机密度,TOT为辐射信号驻留时间,TI为截获接收机扫描时间,NI为辐射信号的频率跳变次数,NF为处于瞬时扫描带宽中辐射信号频率跳变次数,C0为覆盖区/灵敏度比例因素。
仿真3截获概率比较
初始参数设置为M=11.2m2,PI=-113dBW,DI=0.001,TI=4s,C0=0.477。辐射源和截获接收机一直处于工作状态,辐射信号驻留时间TOT=TI。则常规跳频信号和四维超混沌信号在不同距离的截获概率对比曲线如图7所示。
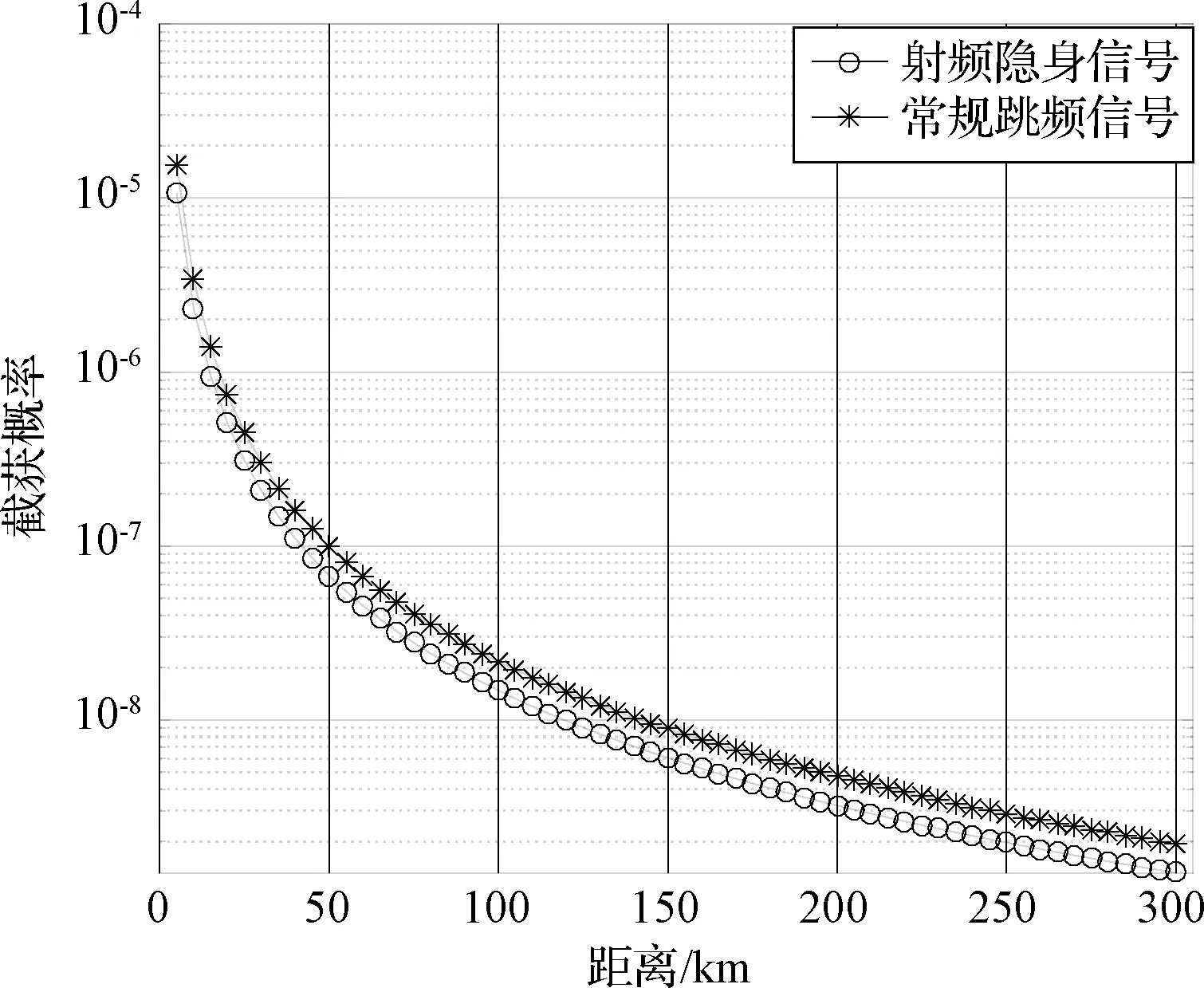
图7 截获概率对比Fig.7 Comparison of intercept probability
根据图7仿真数据,计算四维超混沌信号截获概率ψr,相比于常规跳频信号截获概率ψc的降低比例,公式如式5所示。
(18)
四维超混沌信号和常规跳频信号在不同距离的截获概率数值如下表5所示。
由图7和表5仿真数据可知,四维超混沌系统在不同距离下的截获概率始终低于常规跳频信号,且其截获概率优于常规跳频信号30%以上。因此,本文所提的四维超混沌跳频信号具有较好的抗截获能力。
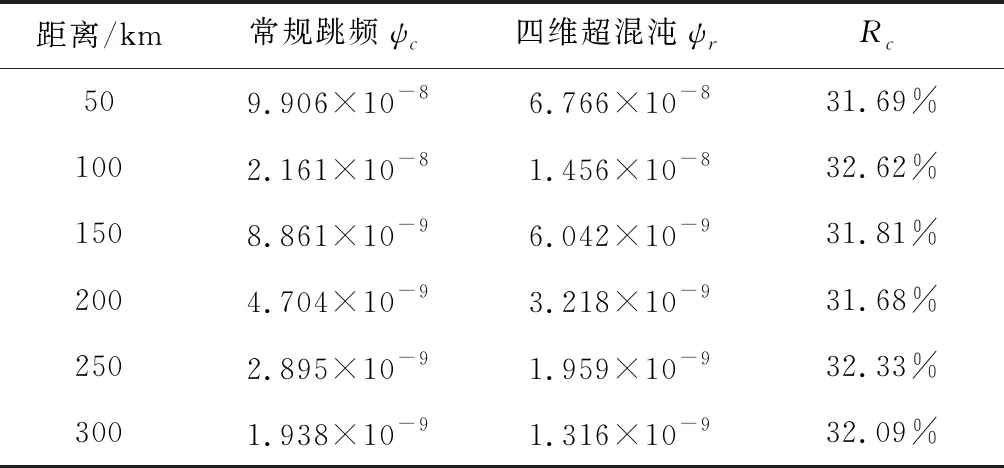
表5 两种系统在不同距离下的截获概率Table 5 Intercept probability of two systems at different distances
4 结论
本文从提高跳频通信系统频率特征不确定性入手,构建四维超混沌系统以解决传统混沌系统的复杂性有限和短周期问题。四维超混沌系统扩展了系统解空间,有效增加了系统复杂度,并通过引入周期性扰动措施,使原系统跳出系统状态的闭合状态集,解决了传统混沌系统的短周期现象。最后,在四维超混沌系统的基础上,提出了跳频系统频率序列和周期序列的联合不确定设计方法。仿真结果表明,本文构建的四维超混沌系统与Logistic、Lorenz混沌系统相比,具有最大近似熵值,复杂度性能最优;四维超混沌系统与Lorenz混沌系统相比,在相同有限精度条件下,周期性能明显减弱,有效消除了系统的短周期现象。基于四维超混沌的跳频系统与常规跳频系统相比,不同距离下的截获概率均可提高30%以上,具有较好的射频隐身性能,可以有效提高飞行器平台的生存能力。

