基于地形匹配的高超声速飞行器初始定向偏差在线辨识方法

鲜 勇，任乐亮，郭玮林，张大巧，杨子成

(火箭军工程大学作战保障学院，西安 710025)

0 引 言

高超声速飞行器能够长时间在临近空间滑翔飞行，射程远，突防能力强，受到各国高度重视[1-2]。在有效突防的情况下，高精度命中目标将会带来成倍的作战效能[3]。而在长时间、大过载的飞行情况下，受到惯性系统制造工艺的限制，纯惯性导航方式将无法满足精度要求。文献[4]展望了高超声速飞行器的组合导航方式，如惯性/卫星、惯性/地形匹配等。卫星导航系统精度高，但抗干扰能力差；地形匹配导航系统具有较强的抗干扰能力、较高的导航定位精度和较好的隐蔽性[5]。考虑到高超声速飞行器的导航系统应具有较强的抗干扰能力，因此，本文围绕高超声速飞行器惯性/地形匹配组合导航方式进行研究。

在大初始定向偏差情况下，利用地形匹配定位结果修正惯性系统误差，将大幅度减小惯性全程机动飞行累积的惯性误差[5-7]，但是并未对惯性系统本身进行校正，在后期飞行过程中误差累计明显。

惯性系统初始定向偏差的大小，与高超声速飞行器自主定向时间紧密相关[8-10]，在机动发射条件下，自主定向时间越短越好，但同时会带来自主定向精度的下降，而惯性系统初始定向偏差将会直接影响导航精度[11-12]。文献[8-9,13]以卡尔曼滤波算法为基础，对快速定向问题进行了研究，较传统方法有所提高，如文献[13]设计了一种粗对准+精对准的初始对准方案，其调平及定向精度均较高，但仍需较长的地面准备时间。因此，为实现短时瞄准、精确定向，更好的方法是发射后在线辨识并修正初始定向偏差，将有助于提高机动发射适应性。

学者们多依托组合导航系统对初始定向偏差进行在线辨识，如文献[11]结合GPS信息，采用数值优化的方法在线辨识初始定向偏差，辨识精度高且辨识效果稳定；文献[14]基于弹载SINS/GPS系统，较好地解决了空中快速对准(包含定向)问题。而据公开资料显示，高超声速飞行器组合导航研究较多，但多集中于以卫星和天文导航[15-17]为辅助信息，对地形匹配导航方式研究较少。针对高超声速飞行器飞行环境复杂的特点，文献[15]和文献[16]分别以地理坐标系和发射惯性坐标系为导航坐标系，利用星敏感器的高精度姿态信息实现了初始定向偏差的高精度辨识；文献[17]研究了SINS/BDS/CNS组合导航模型，由于引入卫星导航信息，具有很高的定姿、测速和定位精度。但上述文献中所采用的卫星导航信息易受干扰，战时存在较大风险。地形匹配导航方式的技术成熟度高，具有较高的发展前景，因此，本文借鉴以上研究成果，主要讨论了利用地形匹配导航信息在线辨识初始定向偏差的方法。

以发射惯性坐标系[16]为导航坐标系，首先建立惯性系统导航误差模型和初始对准误差模型，通过分析初始定向偏差对导航精度影响机理，融合相邻两个地形匹配区两次地形匹配定位信息，对初始定向偏差进行辨识，并对辨识精度影响因素进行分析。最后，以CAV-H为仿真对象，建立全弹道仿真模块，加入惯性/地形匹配组合导航模型，对初始定向偏差辨识效果进行验证。

1 综合姿态控制的惯性系统导航误差模型

1.1 惯性系统工具误差计算模型

在高超声速飞行器滑翔飞行段，本文采用文献[18]给出的捷联惯性系统实用模型，其陀螺仪误差模型和加速度计误差模型如下。

1)陀螺仪误差模型

(1)

2)加速度计误差模型

(2)

文献[16,19]指出，高超声速飞行器通常采用惯性坐标系作为导航坐标系，因此，建立工具误差计算模型后，在发射惯性坐标系进行导航解算，导航解算模型见参考文献[3,18,20]。

激光捷联惯性系统导航误差主要由激光陀螺测量角度误差引起的坐标转换误差以及由加速度计测量的视加速度偏差组成。由于陀螺仪角度测量值存在偏差，因此，除引起坐标转换误差外，还将引起姿态控制偏差。考虑到高超声速飞行器滑翔段受空气动力作用，姿态控制偏差将使得实际升力、阻力和侧力与标准弹道相应值不同，因此，针对飞行时间长、航程大的特点，使用标准弹道视加速度作为惯性系统误差模型激励值将会有较大偏差。本文使用实际弹道结合姿态控制偏差，按照相应动力学模型[20]，计算得到实际视加速度，将更符合实际飞行导航状态。

1.2 初始对准误差计算模型

初始对准误差包括水平基准的初始俯仰角误差Δφ0、初始偏航角误差ψ0和定向基准的初始滚动角误差γ0[20]，本文所讨论的初始定向偏差ΔAmz=-γ0。由初始对准引起的导航偏差包括几何因素和动力学因素两方面[3]。

采用含有初始定向偏差的发射惯性坐标系作为导航计算基准，由于初始定向偏差的存在，使得导航坐标系与标准发射惯性坐标系之间存在偏差，其几何影响关系如式(3)所示。

(3)

(4)

其中，

(5)

为加入动力学影响因素，根据发射系下动力学方程[20]，需要重新计算地球自转角速度在实际发射坐标系各轴投影，如式(6)所示。

(6)

(7)

综合姿态控制的惯性系统导航误差模型仿真流程如图1所示。

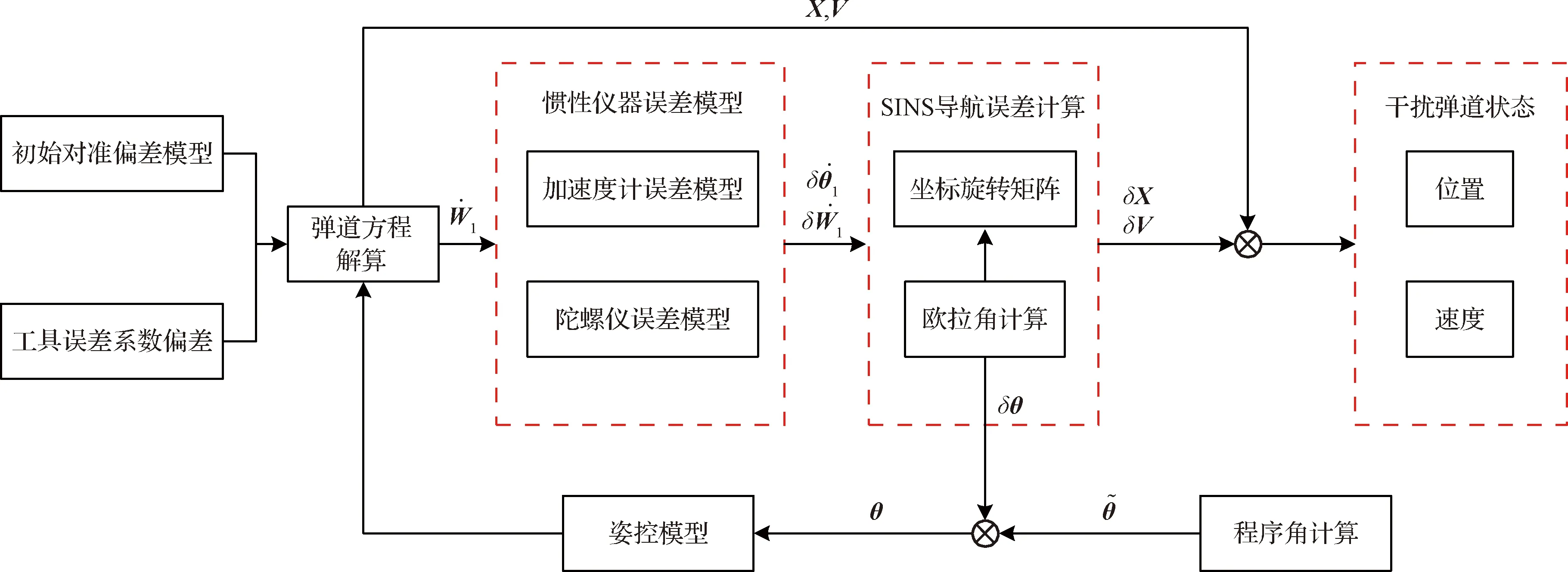
图1 惯性系统导航误差仿真流程Fig.1 Simulation flow of navigation error of inertial system

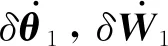
2 基于地形匹配的初识定向误差在线辨识模型

机动发射条件下，为提高武器系统生存能力，应尽可能缩短发射准备时间，在采用高超声速飞行器自主初始对准、无依托发射模式下，如何快速且高精度自对准成为亟待解决的问题。文献[21]指出水平对准速度快，精度高，而方位对准慢，精度差，因此，影响机动发射快速性以及导航精度的主要初始对准因素是初始定向。本文提出初始定向在线辨识方法，在短时自主定向情况下，仍能够保持较高的导航精度。

地形匹配导航系统能够以较高精度给出实际弹下点位置，通过一定的坐标转换，可以对惯性系统累计误差进行补偿，文献[5]对地形匹配系统进行过详细介绍。高超声速飞行器在滑翔飞行阶段进行地形匹配，由于其飞行高度在30～50 km范围[16]，需要合理设计地形匹配导航系统以完成高精度匹配。本文研究重点是利用地形匹配定位信息进行初始定向在线辨识模型，因此，未对地形匹配定位精度进行研究。

2.1 仅考虑初始定向偏差情况

假设高超声速飞行器进入滑翔段后，两个相邻地形匹配区分别为D1和D2，两个地形匹配区间隔为ΔL12。在本节中假设仅考虑初始定向偏差，无工具误差系数偏差且地形匹配误差为0。

在单个地形匹配区内实现初始定向辨识将面临以下问题：

1)需大量匹配定位结果，测高雷达需要长时间连续开机，将导致单个地形匹配区长度较大，不利于匹配区适配性评估。

2)在考虑地形匹配定位误差后，由于匹配区内匹配定位点之间距离较小，导致地形匹配系统给出的方位向信息会有较大偏差。

本文利用两个地形匹配区进行初始定向辨识，不需要大量匹配定位结果，同时，可以降低地形匹配误差对辨识精度的影响。

为实现初始定向在线辨识，其工作过程如下：高超声速飞行器在初始定向辨识过程中不进行横向机动，在匹配区D1根据地形匹配定位结果进行一次位置修正，消除由几何因素和动力学因素累计的误差；结合在匹配区D2内定位结果，对初始定向偏差进行辨识，如图2所示。

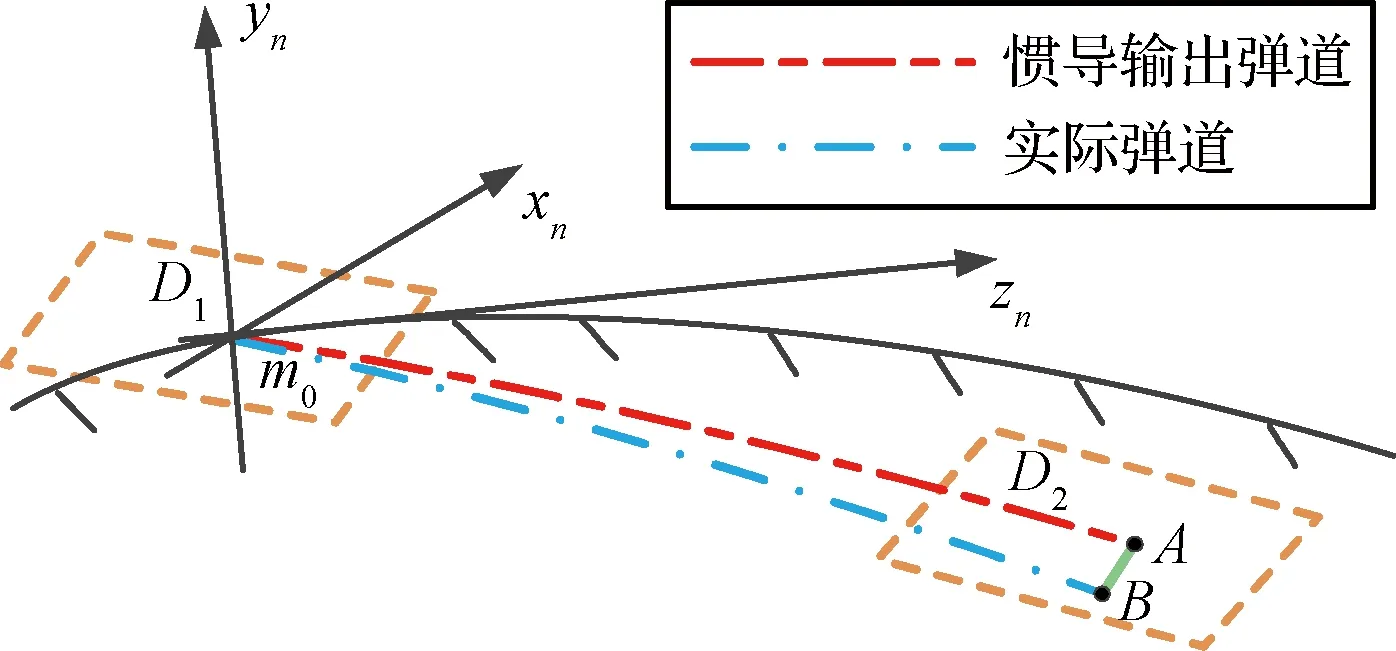
图2 初始定向偏差在线辨识模型示意图Fig.2 Schematic diagram of initial directional error on-line identification model

首先以标准弹道在匹配区D1的定位点m0为坐标原点，建立北东坐标系m0-xnynzn，匹配区D2中惯导解算并进行坐标转换得到A点的地心大地直角坐标系坐标为(xsa,ysa,zsa)，根据式(8)将其转化到坐标系m0-xnynzn，得到(xna,yna,zna)。

(8)

其中，

(9)

式中：xna,yna,zna为北东坐标系下的坐标，φsm,λsm分别为m0点的地心纬度和地心经度，re为φsm下的地球半径。

由于初始定向偏差的存在，实际弹下点轨迹与惯导输出弹下点轨迹不同，在匹配区D2内定位点为B，坐标系m0-xnynzn下的坐标为(xnb,ynb,znb)。弹下点偏离到B的原因包括几何因素和动力学因素，考虑到匹配区D1消除过惯性系统累计误差且两个匹配区间隔不远，因此，可以忽略动力学因素引起的偏差，仿真结果同样可以验证此结论。

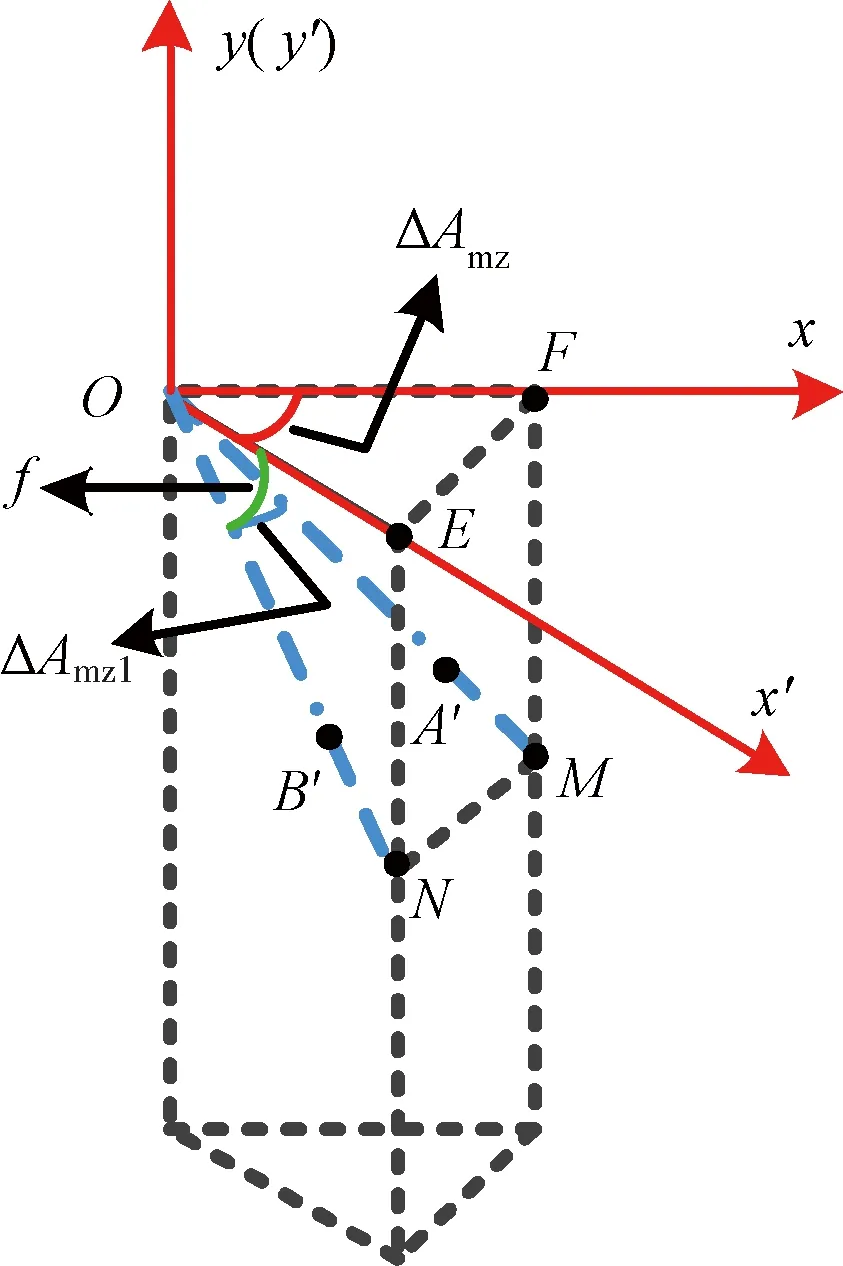
图3 几何因素引起的导航偏差示意图Fig.3 Diagram of navigation deviation caused by geometric factors

通过几何关系不难得到，

(10)

其中，

(11)

证. 在图3中，作OE=OF，ON与OE夹角为f，OM与OF夹角为f，∠EOF=ΔAmz，∠MON≈ΔAmz1。

由余弦定理可得

EF2=OE2+OF2-2OE·OF·cos∠EOF
MN2=OM2+ON2-2OM·ON·cos∠MON

所以cos∠MON=1-(1-cos∠EOF)cos2f

2.2 考虑初始调平和工具误差系数偏差情况

实际飞行过程中，将存在初始调平偏差和惯性系统工具误差系数偏差。在分析过程中，假设匹配区D1的定位点m0与发射系原点重合，那么初始对准偏差引起的横向偏差可以由发射系z轴坐标间接反映，如式(12)所示。

Z′=-cosψ0sinγ0·X-sinψ0·Y+cosψ0cosγ0·Z

(12)

式中：(X,Y,Z)为高超声速飞行器在实际发射坐标系位置坐标，Z′为在标准发射坐标系z轴坐标。由于ψ0，γ0为小量，可得sinψ0≈ψ0，cosψ0≈1，sinγ0≈γ0，cosγ0≈1。

移项后并略去二次小量得

ΔZ≈-γ0X-ψ0Y

(13)

在大初始定向偏差、精确初始调平条件下，|ψ0|远小于|γ0|，进入滑翔段后短时间内，一般|Y|小于|X|，做进一步简化可得

ΔZ≈-γ0X

(14)

可以得到，由几何因素影响引起的横向偏差，主要与初始定向偏差有关。

考虑工具误差系数偏差后，新的角度偏差ΔAmz2由两部分组成，一部分是由初始定向偏差引起，另一部分是由工具误差引起，如式(15)所示。

ΔAmz2=ΔAmz+ΔAIMU

(15)

其中，ΔAIMU为惯性测量系统在两个匹配区间累积误差造成的角度计算偏差，可以由式(16)进行估计。

(16)

式中：ΔH12为惯性测量系统在两个匹配区间累积的横向偏差。

在假定ΔAmz2=ΔAmz1后，对初始方位角进行修正，将会多修正ΔAIMU一项，而考虑到工具误差系数偏差服从均值为0的正态分布，由大数定理可得，ΔAIMU成服从正态分布且E{ΔAIMU}=0，在统计特性上

E{ΔAmz2}=E{ΔAmz1}

(17)

由式(17)可知，在考虑工具误差系数偏差后，虽然没有得到初始定向偏差的准确值，但是在统计特性方面，仍然将初始定向偏差有效分离，能够提高命中精度。

2.3 考虑地形匹配定位偏差情况

根据前面分析，在不考虑地形匹配定位偏差情况下，本文模型能够准确辨识初始定向偏差，在实际飞行过程中，地形匹配定位结果存在偏差。假设在匹配区D1横向定位偏差为Δd1，匹配区D2横向定位偏差为Δd2，沿飞行方向偏右为正。

ΔAmz3=ΔAmz+ΔAIMU+ΔAT

(18)

其中，ΔAT为地形匹配横向定位偏差引起的角度计算偏差，可以根据式(19)进行估计。

(19)

ΔAT的存在，会降低初始定向辨识精度，ΔAT的大小如表1所示，由表1和式(19)可以得到，|Δd2-Δd1|一定，ΔL12越大ΔAT越小，而ΔL12需要结合地形匹配区选取、滑翔段弹道规划等进行综合考虑。为保证本文模型辨识精度，ΔL12是滑翔段任务规划约束条件之一，同时，减小地形匹配定位误差也是提高辨识精度途径之一。

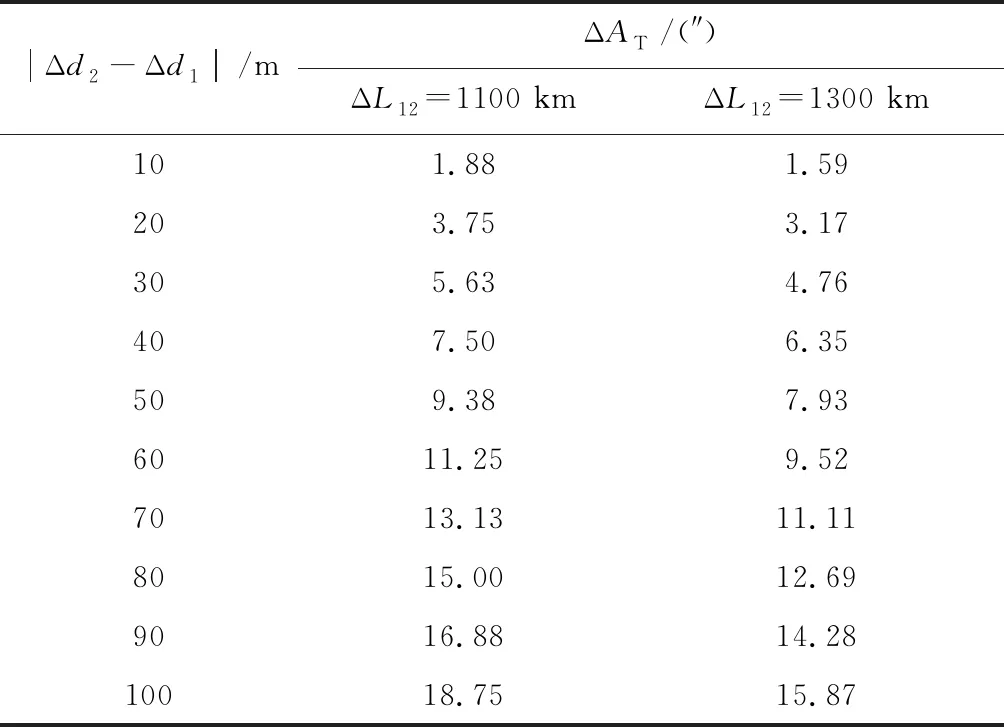
表1 地形匹配定位偏差引起的角度计算偏差Table 1 Angle calculation error caused by terrain matching positioning error

3 仿真校验

本文以美国高超声速飞行器CAV-H为仿真对象，相关参数见文献[22-23]，攻角模型采用文献[24]中的线性函数模型，采用火箭实现助推段高精度入轨，设计方法见参考文献[25]，惯性系统工具误差系数偏差[17]如表2所示。

表2 工具误差系数精度Table 2 Instrumental error coefficient accuracy

首先设定仿真条件为ΔAmz～N(0,502)(″)，ΔL12=1300 km，加入15″(3σ)的初始调平偏差，不考虑工具误差系数偏差和定位误差，进行5000次蒙特卡洛仿真。图4给出了初始定向偏差和经过辨识后剩余定向偏差关系，剩余定向偏差中包含由于初始调平误差和动力学因素影响引起的辨识偏差。将剩余偏差取绝对值后，平均值为3.01″，最大值为10.73″，可以看出辨识效果很好，并能够验证忽略动力学因素影响的可行性。

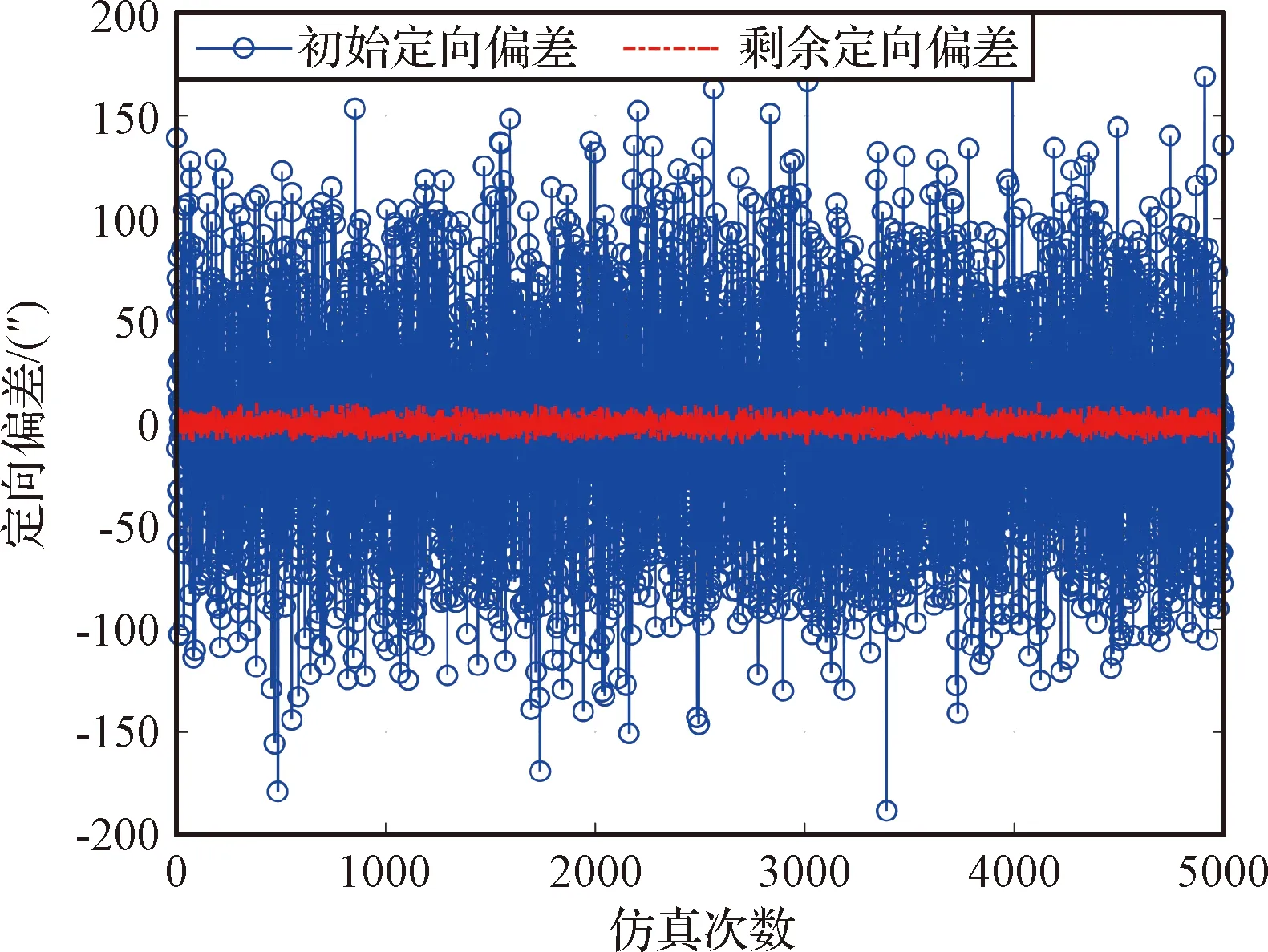
图4 初始定向偏差辨识结果Fig.4 Initial directional error identification results

为检验加入惯性系统工具误差系数偏差后，能否有效分离初始定向偏差，令ΔAmz=-150″，根据表2加入工具误差系数偏差，采用蒙特卡洛法仿真5000次。在惯性系统工作状态相同的情况下，在飞出匹配区D2之后，在惯性系统工作状态相同的情况下，将不修正初始定向偏差(仅修正位置偏差)后继续飞行一定距离的横向偏差记为ΔH1，修正初始定向偏差(ΔAmz2)后继续飞行一定距离的横向偏差记为ΔH2，仿真结果如图5～图6所示。

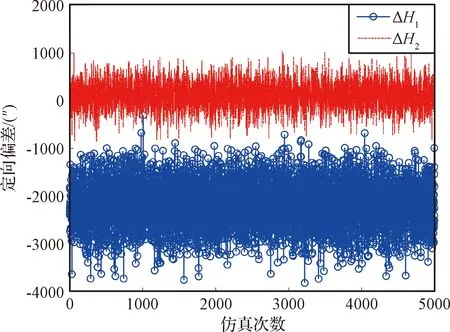
图5 ΔH1和ΔH2仿真结果(ΔAmz=-150″)Fig.5 Simulation results of ΔH1 and ΔH2(ΔAmz=-150″)

图6 ΔH1和ΔH2直方图(ΔAmz=-150″)Fig.6 Histogram of ΔH1 and ΔH2(ΔAmz=-150″)

从图5可以看出，ΔH1和ΔH2的大小关系，ΔH1平均偏差为-2187.9 m，标准差为465.0 m，ΔH2平均偏差为112.1 m，标准差为284.9 m，图6给出了ΔH1和ΔH2的直方图，可以看出，将ΔAmz2视为初始定向偏差，并进行修正后，横向偏差分布将进行平移，该平移量是由初始定向偏差引起的，可以达到无初始定向偏差情况下的落点精度。结合图5和图6可以看出，ΔH1标准差要小于ΔH2的标准差，除修正了初始定向偏差外，对工具误差系数偏差也有一定的补偿，总体导航精度提高明显。

本文在此基础上，对初始定向偏差为120″,60″,-120″,-60″的情况进行了仿真，图7给出了每种情况下横向偏差关系，表3给出了ΔH1和ΔH2的均值与标准差，可以看出，ΔH1均值的绝对值较大，而ΔH2均值在0附近，说明已经基本消除了初始定向偏差对落点的影响，ΔH2标准差基本相等，说明不同初始定向偏差对辨识效果影响不大，具有一定的适应性。

表3 ΔH1和ΔH2的均值与标准差Table 3 Mean and standard deviation of ΔH1 and ΔH2

为说明地形匹配定位误差对辨识效果的影响，本文通过搭建的惯性/地形匹配仿真系统进行校验，设置仿真条件为：ΔAmz～N(0,502)(″)，ΔL12=1330 km，加入15″(3σ)的初始调平偏差，无工具误差系数偏差，得到5000次仿真结果。地形匹配横向定位偏差如表4所示，辨识结果如图8所示，将剩余定向偏差取绝对值后，平均值为8.42″，最大值为34.65″，较初始定向偏差仍有大幅减小，但定位误差的存在会降低辨识精度，因此，提高定位精度将会改善辨识效果。

图8 考虑地形匹配定位偏差的辨识结果Fig.8 Identification results under the condition of considering terrain matching positioning error

4 结 论

本文融合相邻两个地形匹配区两次地形匹配定位结果，建立了高超声速飞行器机动发射条件下初始定向偏差在线辨识模型。在不考虑地形匹配定位误差情况下，将初始定向剩余偏差取绝对值后，其平均值为3.01″，最大值为10.73″；考虑地形匹配定位误差为173.88 m(3σ)情况下，初始定向剩余偏差平均值为8.42″，最大值为34.65″。因此，在统计意义上，工具误差系数偏差不会影响本文模型的辨识效果，但是地形匹配定位误差会降低辨识精度。

本文建立的模型能够较好地解决机动发射条件下初始定向偏差较大的问题，对提高高超声速飞行器导航精度有一定的参考价值。同时，需要指出的是，本文模型不是独立的，需要综合考虑滑翔段弹道规划、地形匹配区选取和相邻两个地形匹配区间隔等因素来确定。适配性差的地形匹配区将降低定位精度，下一步将对考虑高超声速飞行器弹道特点和测高雷达性能的地形匹配区快速选取方法进行研究，从而降低任务规划准备时间，提高匹配区适配性和初始定向偏差辨识精度。