条带式太阳帆航天器的热致结构动力学响应
张军徽,方瑞颖,武 娜,佟 安,刘应华
(1. 北方工业大学土木工程学院,北京100144;2. 清华大学航天航空学院,北京100084)
0 引 言
依靠光压推进,太阳帆航天器通常被认为适宜于星际航行[1],目前绝大多数的太阳帆任务围绕深空探测[2-4]、人工拉格朗日点[5-6]开展相关研究。在这些研究中,太阳帆的地球逃逸出发轨道通常被设定在高度介于2000~36000 km的地球同步转移轨道[7],然而,地球同步转移轨道的发射成本高昂,这迫使研究者开始考虑将太阳帆发射至600~900 km 的近地轨道(Low Earth orbit,LEO),依靠太阳帆自身的多圈螺旋飞行实现地球逃逸[8]。2019年7月31日美国行星协会宣布LightSail 2成为世界上第一个仅依靠光压实现升轨的近地轨道航天器[9]。另一方面,运行于近地轨道的太阳帆任务也逐渐引起人们的兴趣,Matloff等[10]提出将近地轨道太阳帆作为行星采样任务返回阶段的空中刹车(Planetary aerobrake);Macdonald等[11]提出利用近地轨道太阳帆实现对地球磁尾的长时观测;Lappas等[12]提出了将近地轨道太阳帆用于卫星寿命末期使卫星脱轨的拖拽帆;文献[13-15]提出利用太阳帆清除近地轨道日益增多的太空垃圾。在国内,龚胜平等[16]研究了利用太阳帆实现地球同步和太阳同步轨道问题;钱航等[17]研究了受地球阴影影响的非理想太阳帆逃逸地球问题。近地轨道太阳帆以其独特的优势正逐渐成为太阳帆研究的热点。
在近地轨道绕地球飞行,航天器将周期性地进出地球阴影,经历空间热环境的剧烈变化,热环境冲击将会引起太阳帆这种大柔性空间结构的动力学响应,进而影响太阳帆航天器的光压推进效率和姿态控制。国内外,关于太阳帆热致结构动力学响应研究的报道较少。Malla和Lin[18]采用有限元方法研究了边长100 m×100 m四边形太阳帆在温度场均匀变化下的结构响应,桅杆和帆膜热应变的不匹配引起了显著的横向结构变形。Sickinger等[19]对碳纤维增强复合材料(CFRP)太阳帆桅杆的温度场分布、模态特性和屈曲载荷进行了理论和实验研究,研究表明:近地轨道太阳帆桅杆截面温差最大可达150 ℃,温差引起的热应力造成了桅杆屈曲载荷的显著降低,但对桅杆的刚度影响不大。Banik等[20]研究了非均匀分布温度场对太阳帆拓扑结构的影响,以及拓扑结构变化对太阳帆推进效率的影响,当太阳帆姿态角达到35°时,非均匀温度场在结构内部引起了较大的热应变,造成了桅杆变形的增大。Stohlman和Loper[21]研究了一种三角形截面可展太阳帆桅杆(Triangular rollable and collapsible boom,TRAC)的热致变形问题,4 m长的TRAC桅杆在近地轨道的热致变形可达0.5 m,如此大的热致变形将会造成太阳帆姿态的不可控。Stohlman[22]研究了超大型太阳帆桅杆的热致变形问题,指出了对于大型太阳帆桅杆考虑热-结构耦合因素的必要性,给出了联合商业软件进行热-结构耦合分析的方法。Boni等[23]采用有限元方法研究了20 m×20 m方形太阳帆的热致变形问题,结果表明在某些姿态角工况下帆膜的最大热致变形达到15.98 mm。
在国内,太阳帆的研究主要集中在总体设计[24-26]、轨道优化和姿态控制[27-29]等方面,关于太阳帆的结构响应有一些研究。崔乃刚等[30]应用矢量力学基本原理,推导出考虑弹性振动的太阳帆航天器姿态动力学方程,得到了基于控制叶片和控制杆的两类太阳帆航天器的姿态动力学方程。崔祜涛等[31]利用拉格朗日方程建立了太阳帆航天器的姿态动力学模型,对控制杆和反作用飞轮两种三轴姿态控制方案的可控性和稳定性进行了研究。龚胜平等[32]通过设计帆的面积和支撑有效载荷杆的长度,实现太阳帆在轨被动稳定飞行。赵将等[33]采用自然坐标方法和绝对节点坐标方法,对大规模系统动力学方程进行求解,研究了黏弹性太阳帆薄膜自旋展开过程的动力学特性,讨论了薄膜的黏弹性阻尼对自旋展开过程的影响规律。崔乃刚等[34]采用有限元方法对太阳帆支撑管充气展开过程进行了仿真模拟。李纯等[35]采用有限元方法,研究了帆膜应力导入方式及应力大小对太阳帆桅杆屈曲载荷、结构模态、静态变形和帆膜褶皱的影响。马鑫等[36]研究了太阳帆航天器伸展臂对预紧力的屈曲模态分析以及屈曲临界载荷,进行了太阳帆结构的无预紧力结构模态分析与有预紧力结构模态分析。文献[37-38]针对太阳帆单轴大角度机动过程,研究了两种控制方法下太阳帆柔性结构对其姿态控制的影响,研究表明通过端点力控制可以有效减小太阳帆在姿态机动过程中姿态及结构的振动幅度。Yang等[39]建立了边长8 m的太阳帆试验模型,进行了结构静态试验和帆膜褶皱实验,利用试验结果修正了边长160 m太阳帆的有限元模型,给出了160 m太阳帆在光压作用下的静态变形、帆膜褶皱和结构动态响应。

图1 方形太阳帆Fig.1 Square solar sails
条带式太阳帆(见图1(d))是将整体帆膜裁成独立条带型式的方形太阳帆[40],与传统的四点(或五点)式太阳帆(见图1(a))、象限式太阳帆(见图1(b))和连续式太阳帆(见图1(c))相比具有结构效率高、制造简单、易于展开和遭受空间碎片损害风险小的特点,被认为是最理想的太阳帆结构形式[41]。关于条带式太阳帆在近地轨道的热致结构动力学响应研究,国内外未见报道。本文研究条带式太阳帆在近地轨道同时受到太阳热辐射和光压载荷作用下的结构动力学响应,为条带式太阳帆结构设计和姿态控制提供理论依据。
1 理论公式
考虑对称性,如图2所示,取条带式太阳帆的一半进行研究。建立直角坐标系(O-xyz),原点位于太阳帆中心。在每个象限,帆膜被裁成n条宽度为b的平行膜带,由中心至边缘依次编号为1,2,…,n。桅杆的长度为L,膜带与桅杆的连接点将桅杆分为n段长度为l=L/n的小桅杆段,由中心至自由端依次编号为1,2,…,n。
在后文的瞬态热传导分析和结构动力学分析中,作以下假设:
(1)不考虑膜带褶皱对热量的吸收;
(2)桅杆截面为圆形薄壁,考虑外表面对空间的热辐射,不可考虑内表面之间的热辐射;
(3)忽略膜带与桅杆之间的热传导;
(4)结构变形不影响热量吸收。

图2 条带式太阳帆的一半Fig.2 Half of a stripped solar sail
1.1 桅杆和帆膜的瞬态温度场方程
太阳帆由地球阴影区进入光照区,桅杆受到突加太阳辐射热流S0的作用,如图3所示,θ0是热流入射方向与桅杆外表面法线方向之间的夹角。

图3 热辐射作用下的薄壁桅杆Fig.3 Thin-walled boom subjected to solar heat flux
根据假设(2)和(4),忽略薄壁截面厚度方向的温度变化,桅杆的温度场Tb沿x向均匀分布,在截面内满足如下非线性偏微分方程:
(1)
式中:c为桅杆的比热容,ρ为桅杆的密度,t为时间,k为桅杆的热传导系数,r为桅杆截面的平均半径,φ为桅杆截面的轴向角坐标,ε为桅杆外表面的热辐射系数,σ为斯蒂芬-玻尔兹曼常数,h为桅杆截面壁厚,αs为桅杆外表面的热吸收系数。
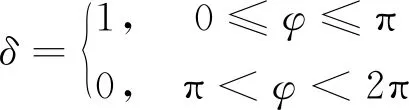
(2)
设Tb(φ,t)可表示为:
Tb(φ,t)=Ta(t)+Tp(t)sinφ
(3)
式中:Ta称为桅杆截面的平均温度,Tp称为桅杆截面的摄动温度。
将式(3)代入式(1),并对桅杆截面进行积分,可得如下两个解耦的常微分方程:
(4a)
(4b)
其初始条件为Ta(0)=T0,Tp(0)=0。易得Ta的稳态温度为:
(5)
采用文献[42]的方法,摄动温度Tp的解为:
(6)
其中:
(7a)
(7b)
对于帆膜,忽略膜厚方向的温度变化,其温度场Tm均匀分布,满足如下方程:
(8)
式中:εm为帆膜的热辐射系数,ρm为帆膜的密度,cm为帆膜的比热容,tm为帆膜的厚度,αm为帆膜的热吸收系数。
由于帆膜的厚度和热容很小,在太阳热流S0作用下,迅速达到稳态温度:
(9)
1.2 桅杆和膜带的振动方程
帆膜的温度变化,会引起帆膜内预应力的变化。设帆膜的初始预应力为σ0,在热辐射作用下变为:
(10)
式中:αm为帆膜的热膨胀系数,Em为帆膜的弹性模量。
预应力为σm的窄条膜带在太阳光压P0作用下的振动可看作是张力为T=σmbtm的弦振动,对于第i条膜带,其简化为弦的振动方程是:
(11)
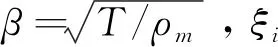
其边界和初始条件为:
(12)

令:
vi(ξi,t)=Vi(ξi,t)+wi(l,t)
(13)
则式(11)变为:
(14)
非齐次边界条件(12)变为齐次边界条件:
(15)
对式(14)进行拉氏变换:
(16)
式中:s为拉氏变换参数。
引入状态向量:
(17)
则式(16)的矩阵形式为:

(18)
其中,
类似地,也将式(15)进行拉氏变换并表示为矩阵形式:
(20)
其中,
根据分布传递函数理论[43- 44],满足式(18)和式(20)的弦振动方程的解为:
(22)
其中,
Msexp(-Fsτ)
(23a)
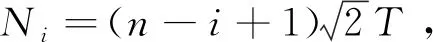
(24)
式中:wi为桅杆的z向位移,E为桅杆的弹性模量,I为桅杆截面的惯性矩,xi为桅杆段的局部坐标,μ为桅杆的阻尼系数。
对式(24)进行拉氏变换:
(25)
引入状态向量:
(26)
则式(25)可写成矩阵形式:
η′i(xi,s)=Fi(s)ηi(xi,s)
(27)
其中,
(28)
根据分布传递函数理论,有:
ηi(xi,s)=exp(Fi(s)xi)ηi(0,s)
(29)
1.3 条带式太阳帆的热-结构动力学方程
图2所示的条带式太阳帆可看作是由n个桅杆-膜带组件依次连接而成,其中第i个桅杆-膜带组件包含第i个小桅杆段和上下对称的两个第i条膜带。在第i个桅杆-膜带组件和第i+1个桅杆-膜带组件的连接处应满足位移连续条件和力平衡条件。其中,位移连续条件为:
(30)
力平衡条件为:
(31)
式(30)中的fi(s)为单根膜带作用在组件连接处的横向力,根据弦振动理论,可由式(17)和式(22)求得:
(32)
其中,
(33a)
(33b)
将式(30)和式(31)表示为矩阵形式:
Ciηi(l,s)+Pi(s)=Diηi+1(0,s)
(34)
式中:
(35a)
(35b)
(35c)
根据式(29)、式(34)可变形为:
(36)
重复使用式(36)有:
(37)
式中:
(38a)
(38b)
Hn-1=I
(38c)
在太阳帆中心施加固定边界条件:
(39)
考虑热应力载荷,桅杆自由端应满足的力边界条件为:
(40)

(41)
式中:αT为桅杆的热膨胀系数。
将式(39)和式(40)表示为矩阵形式:
Lη1(0,s)+Rηn(l,s)+Pn=0
(42)
式中:

(43a)
(43b)
(43c)
根据式(29)、式(37)和式(42)有:
(44)
则在热弯矩载荷和光压载荷作用下太阳帆桅杆自由端的幅频响应可由式(44)求得:
(45)
2 算例分析和讨论
采用本文提出的方法,对边长20 m的条带式太阳帆进行热致结构动力学响应分析,太阳帆的结构尺寸和材料参数见表1。
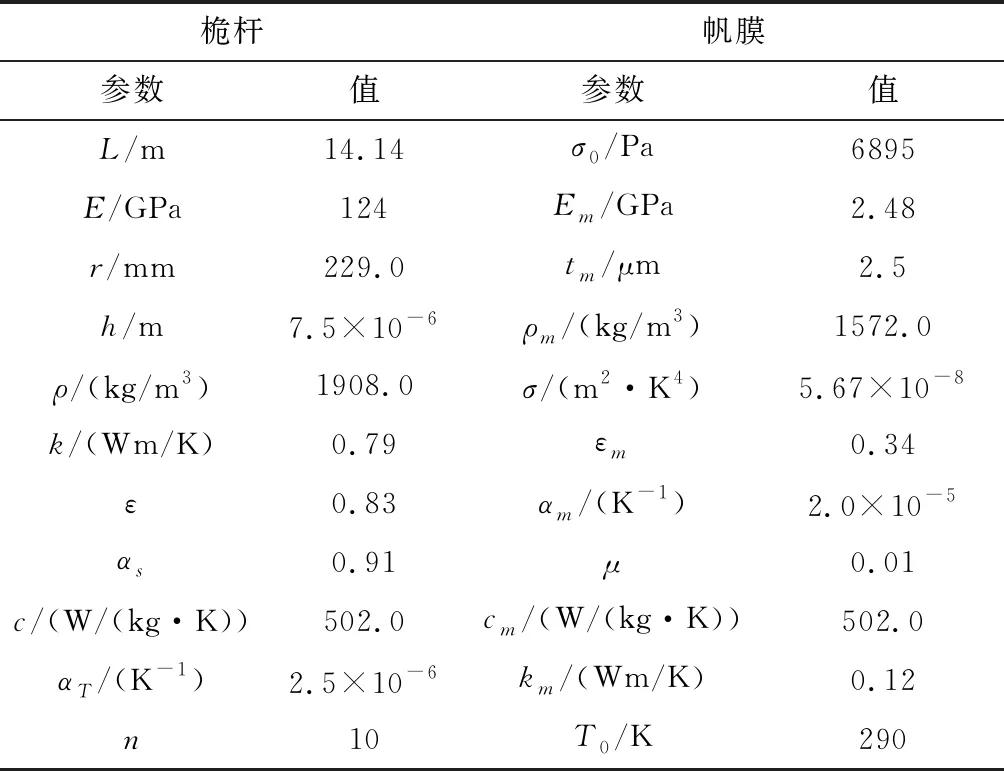
表1 结构尺寸和材料参数[23]Table 1 Dimensions and material properties[23]
2.1 热致结构动力学响应分析
设太阳帆在近地轨道绕地球飞行,以姿态角θ0=0°由地球阴影区进入光照区,受到突加光压P0=9.126×10-6Pa和突加太阳热辐射S0=1360 W/m2的作用,其桅杆自由端的频率响应可根据式(45)求得。
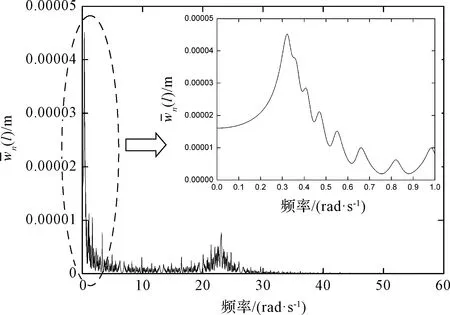
图4 仅光压作用下桅杆端部的幅频响应Fig.4 Frequency response of boom tip subjected to P0
图4给出了仅在光压作用下,太阳帆桅杆自由端的稳态振幅频谱图。由图4可知,仅在光压作用下:太阳帆桅杆的准静态位移为1.60×10-5m;太阳帆桅杆的动态响应振幅很小,最大振幅仅有4.52×10-5m。共振峰处的频率对应于各膜带的自振频率,其中最大共振峰的频率对应于最外侧膜带的自振频率0.33 rad/s。
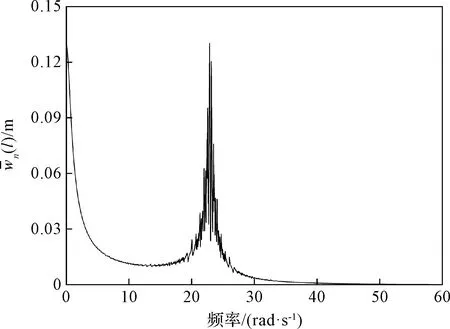
图5 热弯矩和光压作用下桅杆端部的幅频响应Fig.5 Frequency response of boom tip
图5给出了在太阳光压载荷和热辐射共同作用下,太阳帆桅杆自由端的稳态振动幅频图。由图5可知,热弯矩引起的结构动态响应占主导地位。太阳帆发生了频率成分复杂的热致结构振动。
2.2 热致结构动力学响应的影响因素分析
由第2.1节可知,热辐射冲击引起了太阳帆结构明显的热诱发振动响应,这将会影响太阳帆航天器的推进效率、姿态和轨道控制等性能。本节从结构尺寸和材料参数两方面探讨影响太阳帆热致结构动力学响应的因素。

图6 阻尼对桅杆端部幅频响应的影响Fig.6 Effect of damping on frequency response of boom tip
图6给出了阻尼改变对桅杆端部幅频的影响。由图6可知,阻尼改变对桅杆的热致准静态变形没有影响;随着阻尼增大,桅杆振动的一阶振幅明显减小;当桅杆阻尼系数增大至0.3时,振幅的共振峰消失,桅杆响应由热致振动变为热致结构变形;阻尼系数的增大,造成了共振频率的微小降低。
图7给出了桅杆壁厚改变对桅杆端部振幅频谱的影响。由图7可知,壁厚改变对桅杆的热致准静态变形和动态振幅都没有影响;壁厚改变对响应频率的影响也很小。这是由于热应力载荷不是真正的力载荷,而是等效的温度荷载,由式(41)可知,它随着桅杆壁厚的增大同步增大。这表明,通过增大桅杆壁厚来抑制热致结构响应的途径不可行。

图7 壁厚对桅杆端部幅频响应的影响Fig.7 Effect of boom thickness on frequency response of boom tip
图8给出了桅杆热膨胀系数改变对桅杆端部幅频的影响。由图8可知,热膨胀系数的减小显著降低了桅杆的热致准静态变形和稳态振动的振幅;热膨胀系数不改变结构的响应频率。这表明,热膨胀系数是影响太阳帆结构热致响应振幅的关键因素,尽量降低桅杆的热膨胀系数是桅杆设计的重要指标;热膨胀系数小的复合材料将是太阳帆桅杆设计要考虑的重点对象。

图8 热膨胀系数对桅杆端部幅频响应的影响Fig.8 Effect of thermal expansion on frequency response of boom tip
图9给出了太阳帆桅杆长度变大对桅杆端部幅频的影响。由图9可知,随着太阳帆桅杆尺寸的增大,桅杆的热致准静态变形和稳态振动振幅都显著增大;结构的响应频率随着尺寸的增大而降低。这表明,太阳帆的热致结构动态响应是设计大尺寸近地轨道太阳帆必须解决的问题。

图9 桅杆长度对桅杆端部幅频响应的影响Fig.9 Effect of boom length on frequency response of boom tip
3 结 论
随着近地轨道太阳帆任务的提出,本文对条带式太阳帆在近地轨道运行必将面临的热致结构动力学响应问题进行研究。推导了太阳热辐射和光压共同作用下的太阳帆结构动力学方程,给出了太阳帆结构稳态振动幅频响应的计算方法。算例结果表明:热辐射冲击是引起近地轨道太阳帆结构动态响应的主要原因,光压引起的结构响应可忽略不计;增加桅杆壁厚不能有效抑制太阳帆的热致结构动态响应;增大阻尼,减小结构的热膨胀系数能够降低太阳帆热致结构响应的振幅;桅杆长度的增加将显著增大桅杆的热致准静态变形和稳态振动振幅,因此,热致结构动态响应是设计大尺寸近地轨道太阳帆必须解决的问题。

