弹性自驱动卷筒式伸杆机构展开刚度分析及校验

黎 彪，刘志全，张从发，袁 丁，于春宇，李 潇

(中国空间技术研究院总体部，北京 100094)

0 引 言

空间电磁场监测卫星要求星载电场探测仪器和磁场探测仪器(有效载荷)与卫星本体保持一定距离，以降低卫星其它电子设备对星载电磁场探测仪的影响。因此，当电磁场监测卫星进入预定轨道后，需要通过星载伸杆机构的伸展运动将与伸杆末端连接的电磁场探测仪推送到与卫星本体保持一定距离的特定位置上并锁定。套筒式、构架式等传统的星载电机驱动式伸杆机构[1-2]因电机电磁场的引入而不能被应用于该空间探测任务中。传统的弹性元件驱动的多杆铰链式伸杆机构可避免引入电机电磁场的问题，但其因收拢体积大而难以实现“一星多套载荷”的布局，导致其在此类任务中应用受限。薄壁管具有收拢体积小的优点，在此场合下应用本应当具有很好的应用前景，但其中的管状杆(Storable tubular extendable member, STEM)[3-4]、豆荚杆(Collapsible tubular mast, CTM)[5-6]和人字型杆(Triangular roll-able and collapsible, TRAC)[7]均需将弹性元件缠绕在收纳筒上，展开过程均需电机辅助，致使STEM、CTM和TRAC的应用受限；弹性自驱动卷筒式伸杆机构(Spiral tube and actuator for controlled extension and retraction，STACER)具有磁性弱、重量轻、收拢体积小、展开尺寸大等优点，非常适应此种场合[8-9]。然而，其展开后的刚度受构型参数影响。为保证电磁场探测仪器在轨具有良好的位置精度和稳定性，需要弹性自驱动卷筒式伸杆机构具有较高的展开刚度和精度稳定度。因此，开展弹性自驱动卷筒式伸杆机构(下文简称卷筒式伸杆机构)展开刚度的设计与验证具有重要意义。

美国AMETEK Hunter Spring公司在20世纪60年代成功研制出卷筒式伸杆机构，已有600多套机构应用在FAST、Polar、THEMIS、RBSP等卫星的在轨飞行中[10]。但迄今为止，公开文献中未见卷筒式伸杆机构弹性卷筒刚度设计的内容。2010年，中国空间技术研究院与北京科技大学联合攻关，在电磁监测试验卫星中开始研究卷筒式伸杆机构[11]，并已突破了弹性卷筒的加工成型工艺[12]。中国空间技术研究院与北京航空航天大学采用半物理方法建立了弹性卷筒的形函数，基于最小势能原理获得了不同直径弹性卷筒的驱动力变化趋势，但尚未涉及构型参数对弹性卷筒刚度的影响分析[13-14]。清华大学吴江等人基于等螺旋角假设计算了弹性卷筒的展开后长度，随后将其等效为恒截面的悬臂梁，并采用悬臂梁的一阶频率计算公式推算了弹性卷筒的固有频率[15]。但弹性卷筒实物近似为薄壁圆锥，且弹性卷筒不同位置的螺旋角差异较大，这与文献[15]中的假设不符，导致其计算准确性不高。

本文针对卷筒式伸杆机构的展开刚度问题，基于卷筒式伸杆机构工作原理的分析，推导弹性卷筒的刚度与构型参数间的关系，分析弹性卷筒末端螺旋角、末端半径、带厚、带宽对卷筒式伸杆机构展开刚度的影响，以期获得弹性卷筒构型参数对卷筒式伸杆机构展开刚度的影响规律；开展卷筒式伸杆机构展开刚度的试验验证，验证刚度设计分析方法的有效性，为卷筒式伸杆机构的设计与应用提供依据。

1 卷筒式伸杆机构的工作原理

卷筒式伸杆机构主要由弹性卷筒、辅助展开装置，引导杆、储藏筒和压紧释放装置组成，如图1所示。

图1 卷筒式伸杆机构的组成Fig.1 Composition of the STACER

弹性卷筒是由金属弹性带状材料辊弯成形的一种螺旋薄壁管，在外加轴向力和旋转力矩的共同作用下，弹性卷筒可由展开状态(自由态)逐圈收拢在储藏筒中呈收拢状态。引导杆与弹性卷筒间通过螺钉固定。卷筒式伸杆机构呈收拢状态时，压缩收拢在储藏罐中的弹性卷筒积聚了较大的应变能。

当卫星处于发射阶段时，卷筒式伸杆机构呈收拢状态，压紧释放装置将弹性卷筒压紧；当卫星进入预定轨道后，压紧释放装置将解除约束，弹性卷筒的应变能将被释放出来，在辅助展开装置作用下，弹性卷筒经由引导杆导向逐圈向外伸展，实现弹性自驱动卷筒式伸杆机构的展开。

引导杆在机构展开初始阶段起导向作用，确保弹性卷筒的层间具有一定的径向力。辅助展开装置中布置有弹簧，可在展开初始阶段提供额外的驱动力，辅助展开装置能为展开状态的弹性卷筒提供支撑点，以提高伸杆机构的抗弯刚度。

卷筒式伸杆机构的核心部件为弹性卷筒。弹性卷筒的弹性自驱动展开工作原理如图2所示。

图2 弹性卷筒展开工作原理Fig.2 Working principle for deployment of the STACER

在收拢状态下，当第一圈展开后，后续未展开的卷筒一方面在应变能作用下沿着展开方向展开，并且后一圈与前一圈存在重叠区域；另一方面，由于伸杆机构中引导杆的直径略大于弹性卷筒自然状态下的直径，使得成形后的弹性卷筒在径向始终存在正压力，从而保证弹性卷筒层间不发生滑移，最终形成具有较强刚度的薄壁管。

2 弹性卷筒构型参数与刚度的关系式推导

弹性卷筒展开状态的带材为螺旋上升状态，其构型参数主要包括：弹性卷筒的展开长度L,展开后任意处半径R,根部半径R0，末端半径Rt；展开后任意处螺旋角α，根部螺旋角α0,末端螺旋角αt,带宽w和带厚(薄壁带材的厚度)t，如图3和图4所示。

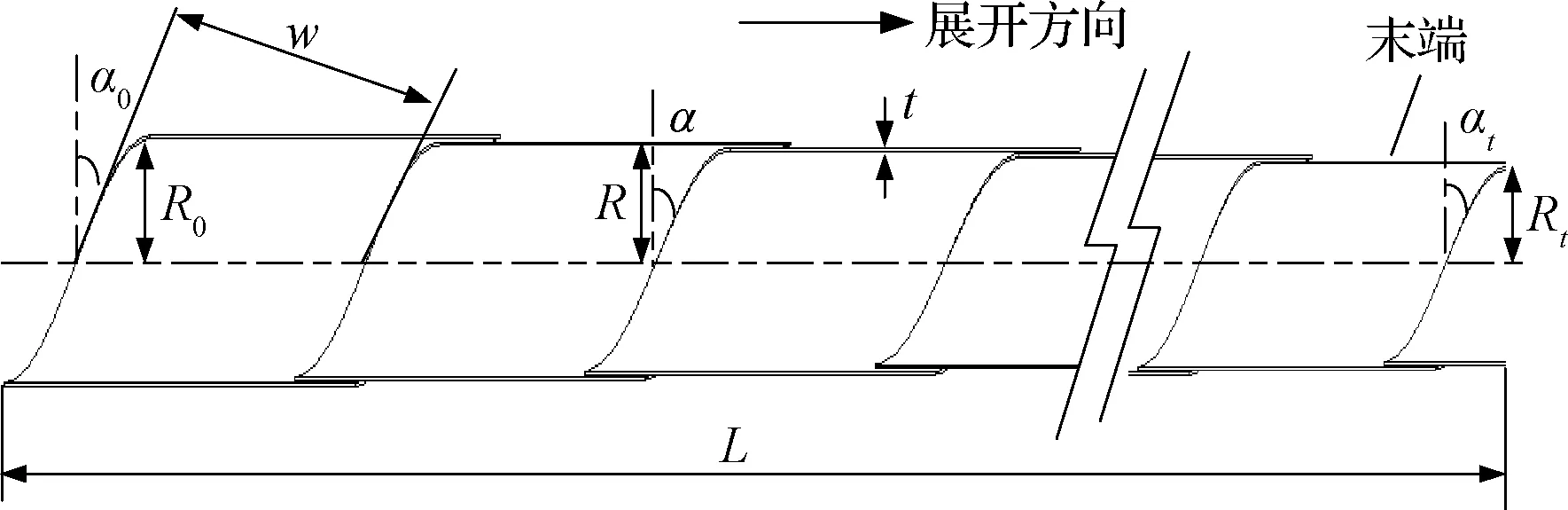
图3 弹性卷筒的构型参数Fig.3 Mechanical parameters on stiffness of STACER

定义δ为展开后相邻两层薄带形成圆锥平均半径的差值，其与带厚t的关系为

δ=t·c

(1)

式中：c为经验系数，可根据实际产品测量而得，可取0.7～0.9。

根据弹性卷筒的实物测量结果，可知展开状态的弹性卷筒边线可近似为等螺距的圆锥螺旋线，则弹性卷筒边线的方程为

(2)

式中：θ为螺旋线的角参量，z为圆锥螺旋线沿着展开方向的高度。p为任意圈螺旋线的螺距，其与当圈螺旋角α和半径R的关系如图4和式(3)所示。

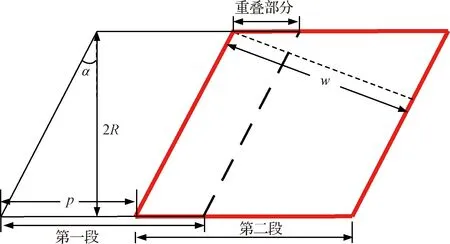
图4 相邻两层弹性卷筒的重叠关系Fig.4 Overlap between adjacent belt

(3)

可知，根部半径R0与根部螺旋角α0,末端半径Rt与末端螺旋角αt均需满足式(3)的关系。且由于展开后末端的螺旋角αt近似于弹性卷筒加工成形的螺旋角，Rt近似于加工成形时弹性卷筒的成形半径。则将αt和Rt分别替换式(3)中的α和R可计算得螺距p，α0由下式确定

p=2πR0·tanα0

(4)

定义重叠率λ为相邻两段螺旋的重叠部分与带宽的比值，则

(5)

可知λ应满足λ∈(0,1)。

展开长度L与螺距p的关系为

L=np+w/cosα0

(6)

式中:n为展开圈数。

圆锥螺旋线的总旋转角度θt为

θt=2πn

(7)

由此，可计算圆锥螺旋线的总长h(加工带长)为

(8)

由于δ≪p，则上式可简化为

(9)

则弹性卷筒的质量m0为

m0=ρ·hwt

(10)

式中：ρ为弹性卷筒带材的密度。

采用瑞利商可计算STACER的圆频率ω的平方为

(11)

式中：E为带材的弹性模量。弹性卷筒任意处截面的惯性矩I(x)为

I(x)=πR3t

(12)

振型试函数y(x)与分布质量下静挠度曲线相似，可表示为

(13)

式中：σ为等效壁厚，其通过将弹性卷筒等效为等壁厚的变截面连续梁，由质量守恒可求得为

(14)

弹性卷筒的展开刚度可采用一阶频率f0表征，则f0为

(15)

联立式(9)～(15)，即可求得刚度与构型参数的关系。

考虑到航天器机构设计中的质量最轻原则，借鉴复合材料比模量的含义，定义弹性卷筒的比弯曲刚度(以下简称比刚度)η用于表征不同构型的弹性卷筒的刚度与质量之间的关系

η=f0/ρL

(16)

式中：ρL为等效线密度

(17)

3 构型参数对展开刚度的影响分析

带材的材料和卷筒式伸杆机构所需的展开长度确定后，可设计的参数仅为带宽w、带材厚度t、末端半径Rt、末端螺旋角αt共4个独立参数。

下文将分析4个独立参数对弹性卷筒的刚度和质量的影响，以获得较优的设计参数。弹性卷筒带材选用高弹性合金钢，其弹性模量E=206 GPa，密度ρ=8400 kg/m3，展开长度L=5 m。各构型参数的变化范围如表1所示。

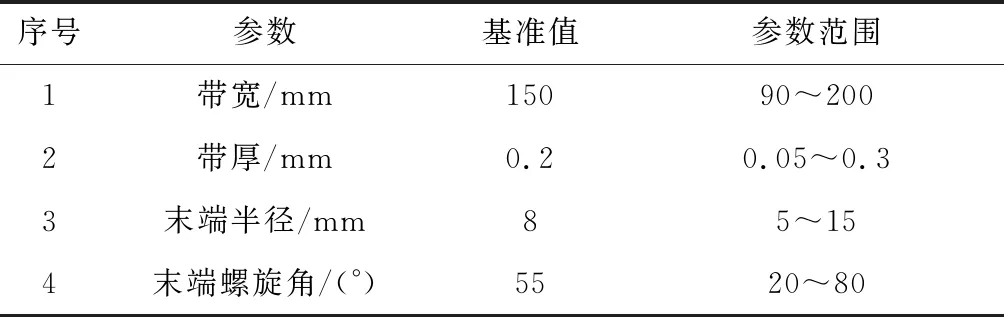
表1 弹性卷筒构型参数的变化范围Table 1 Range of STACER configuration variable

3.1 末端螺旋角对展开刚度的影响

在其余参数不变的情况下，仅改变末端螺旋角αt，可获得末端螺旋角αt与展开刚度的关系如图5所示。

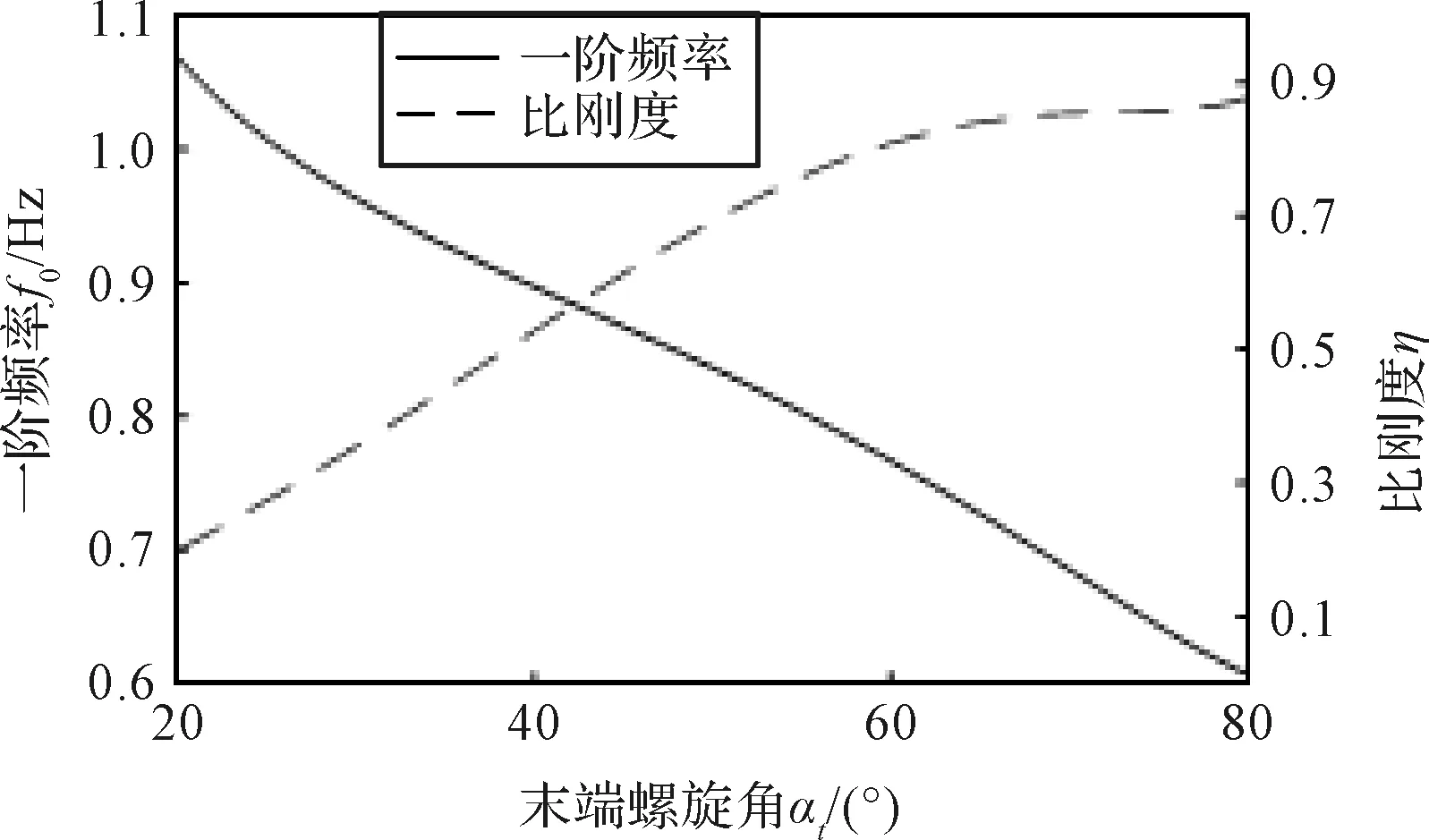
图5 末端螺旋角αt对展开刚度的影响Fig.5 Effect of tip spiral angle on stiffness

由图5可知，随着末端螺旋角αt的增加，弹性卷筒的一阶频率将近似线性下降；另一方面，弹性卷筒的比刚度首先随着末端螺旋角的增加而增加，而当末端螺旋角在62°～75°区间时，比刚度基本不再增加，可获得最优值，具有最高的结构效率。

3.2 末端半径对展开刚度的影响

在其余参数不变的情况下，仅改变末端半径Rt，可获得末端半径Rt与弹性卷筒展开刚度的关系如图6所示。

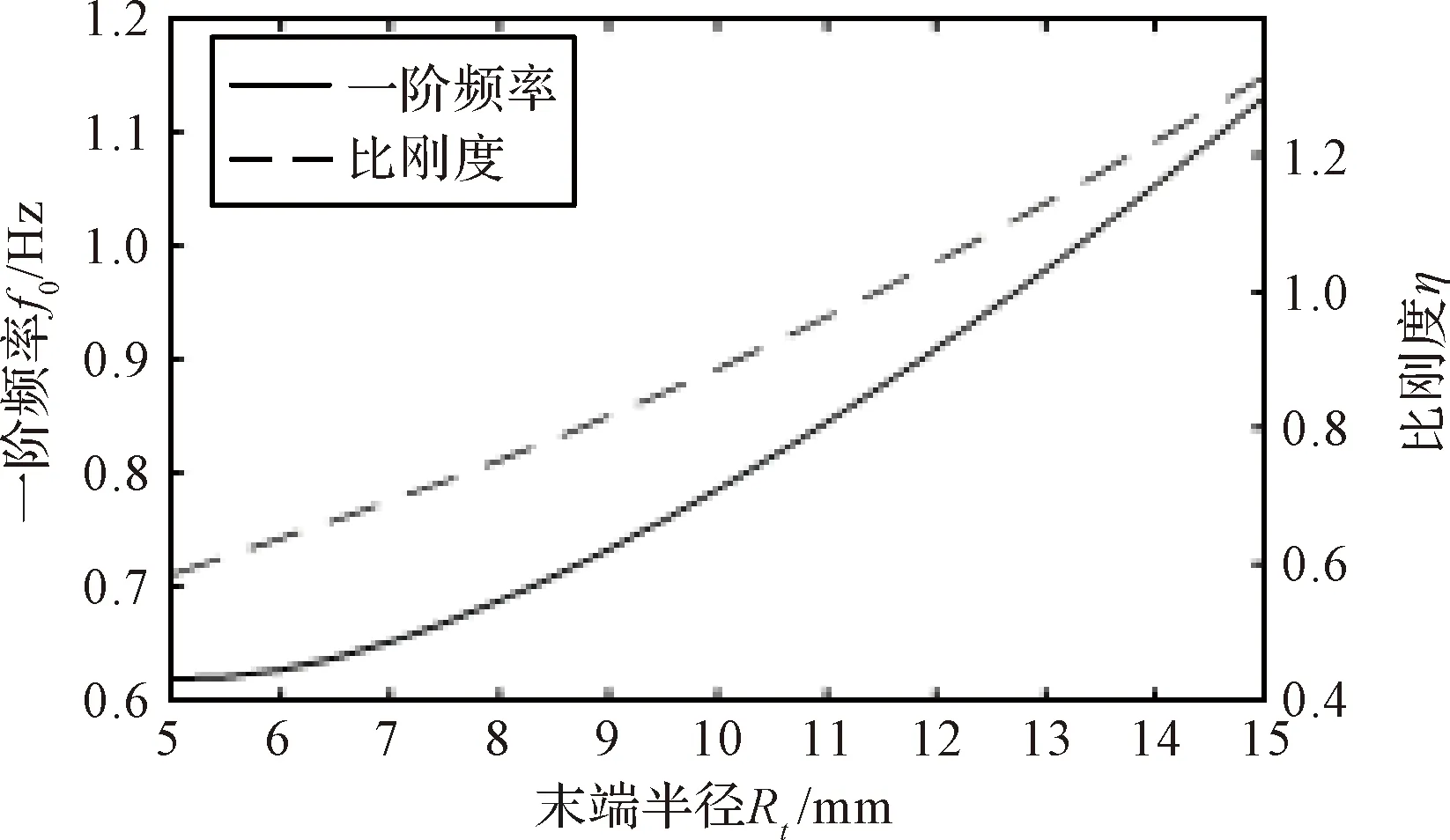
图6 末端半径Rt对展开刚度的影响Fig.6 Effect of tip radius on stiffness

由图6可知，随着末端半径的增加，弹性卷筒的一阶频率和比刚度均一直增加，可知增加末端半径均有利于提升弹性卷筒的刚度和比刚度。

一阶频率随末端半径的增大而近似按照两段不同斜率的直线规律线性增大，在7.5～15 mm区间内，增大的斜率更大。同时，比刚度随末端半径的增大而近似线性增大。

3.3 带厚对展开刚度的影响

仅改变带厚，可获得带厚与展开后频率、比刚度的关系如图7所示。

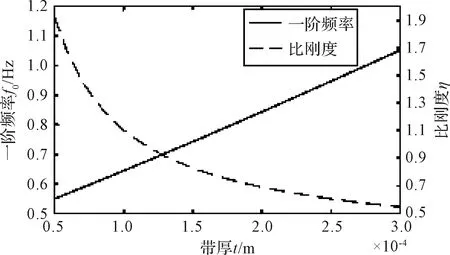
图7 带厚对展开刚度的影响Fig.7 Effect of thickness on stiffness

由图7可知，随着带厚的增加，弹性卷筒的一阶频率也随之线性增加，但弹性卷筒的比刚度将近似按双曲线规律下降。由此可知，在满足一阶频率要求前提下，应尽可能取较小的带厚，以获得较大的比刚度。

3.4 带宽对展开刚度的影响

在其余参数不变的情况下，改变带宽w，可获得带宽w与展开后频率、比刚度的关系如图8所示。

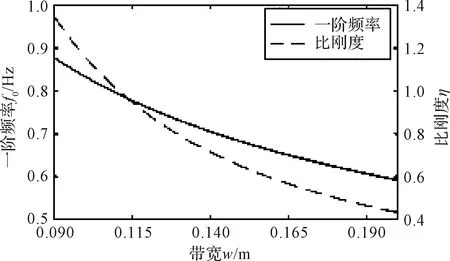
图8 带宽对展开刚度的影响Fig.8 Effect of width on stiffness

由图8可知，随着带宽的增加，弹性卷筒的一阶频率和比刚度均持续下降。由此可知当一阶频率满足要求后，应尽可能取较小的带宽。

同时，随着带宽的减小，由式(5)可知，弹性卷筒相邻层间的重叠率将减小，为保证弹性卷筒在展开后结构连续，一般重叠率应不小于0.2。

3.5 带厚与末端螺旋角度对展开刚度的共同影响

根据上文可知，末端半径应尽可能取大，而带宽应尽可取小。因此，在末端半径和带宽确定后，分析了弹性卷筒一阶频率和比刚度随带厚与末端螺旋角的变化趋势，如图9所示。

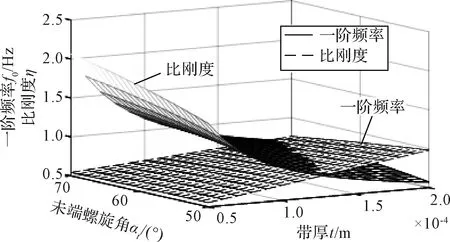
图9 带厚、末端螺旋角度对展开刚度的影响Fig.9 Effect of thickness and tip spiral angle on stiffness

由图9可知，为获取最大的一阶频率，带厚应尽可能增加，螺旋角度应尽可能减小；而与之相反，为获得更大的结构效率即比刚度，带厚应尽可能减小，而螺旋角度应尽可能增大。

4 弹性卷筒构型参数的优化

本文对展开长度为5m的卷筒进行了构型参数的优化，优化设计的数学模型中目标函数为：

g(X)=minm0

(18)

设计变量X为：

X={Rt,w,t,αt}

(19)

式中：各构型参数的可行域如表1所示。

约束条件为：

(20)

式中：D0为弹性卷筒收拢状态的直径，由阿基米德螺线公式计算获得。

在Matlab中通过优化计算获得了一组弹性卷筒的设计参数：末端半径Rt=10 mm；带宽w=125 mm；带厚t=0.15 mm；末端螺旋角αt=65°。

优化后弹性卷筒质量m0=0.72 kg，展开状态一阶频率f0=0.83 Hz。优化前后弹性卷筒的性能比对如表2所示。

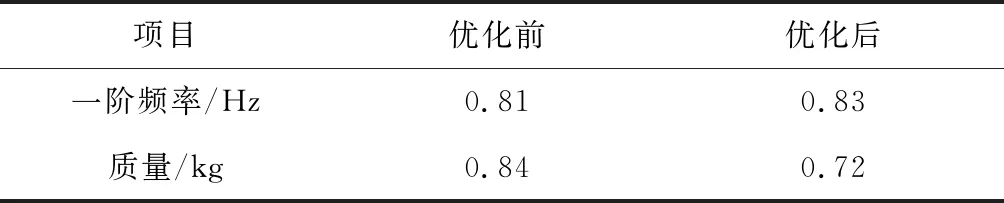
表2 优化前后弹性卷筒性能对比Table 2 Comparison between optimal and original performance of STACER

5 地面试验和飞行试验校验

为了校验卷筒式伸杆机构展开刚度的设计分析的有效性，按照第4节优化后的设计参数研制了一套卷筒式伸杆机构，并开展了如下的地面试验和飞行试验校验。

5.1 地面展开状态刚度测试

为获取弹性卷筒展开后的刚度测试值，按图10(a)的测量原理进行了一阶频率测试。测试过程中，弹性卷筒竖直向上展开，并采用气球浮力抵消重力。采用位移激励法进行了一阶频率测试，即推动试验件末端使其离开平衡位置，然后突然释放，使系统自由振动，通过激光测振仪测量系统自由振动情况，并通过FFT傅里叶变换计算一阶频率。

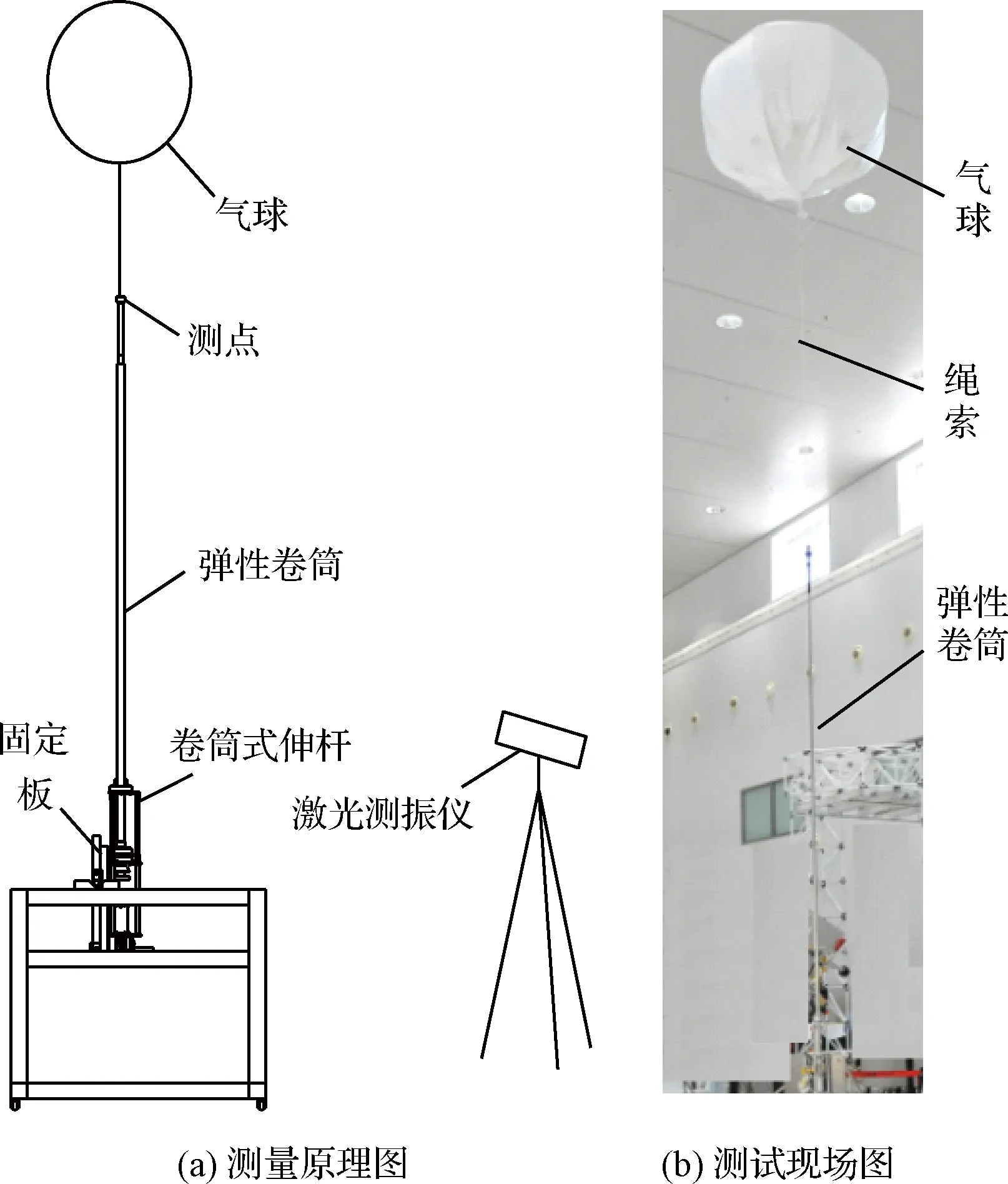
图10 STACER一阶频率测试Fig.10 First-order frequency test of STACER

试验现场如图10(b)所示，一阶频率的实测值和分析值结果如表3所示。

表3 一阶频率试验与分析结果对比Table 3 Comparison between test and analysis results of first-order frequency

由表3可知,卷筒式伸杆机构的一阶频率实测值为0.885 Hz，分析值为0.83 Hz，误差为6.2%，校验了刚度分析结果的正确性。

5.2 热变形测试

由于弹性卷筒由薄带连续层叠成形，当施加温度载荷后，热应力的作用可能导致薄带的层间接触状态发生变化，从而影响成形状态。通过测试不同温度下弹性卷筒末端位移量来评价弹性卷筒的成形状态。测试过程如图11所示，卷筒式伸杆机构展开5 m后，在其周围采用灯阵施加温度载荷，粘贴在弹性卷筒上的热电偶实时监测其温度，并用经纬仪对弹性卷筒末端位置进行测量。

图11 STACER热变形性测试Fig.11 Thermal deformation test of STACER

测试过程中，将展开状态的卷筒式伸杆机构从23 ℃升温至90 ℃，并在60 ℃和90 ℃温度条件下测试了弹性卷筒末端的位移，随后在降温过程中也进行相应的位移测量，按此顺序进行两个循环的试验。试验过程中，弹性卷筒末端的位移变化如图12所示。

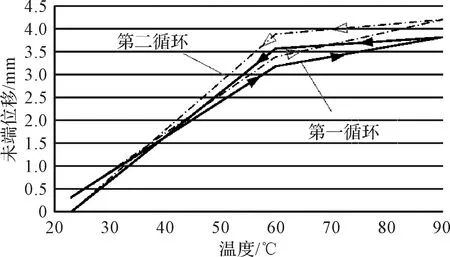
图12 STACER热变形测试结果Fig.12 Thermal deformation results of STACER

由图12可知，在第一个循环中，弹性卷筒经历高温后回至常温，其末端相对初始位置的变形量不超过0.32 mm；在第二个循环后，弹性卷筒末端相对初始位置变形量不超过0.10 mm。由此可知，经历高低温循环载荷后，5 m的弹性卷筒仍能维持住初始状态，即其薄带的层间接触状态未发生显著变化，则弹性卷筒在轨的刚度基本不变。

5.3 飞行试验校验

2018年和2019年，本文所设计的卷筒式伸杆机构分别在“张衡一号”电磁监测试验卫星和“嫦娥四号”着陆器上经受了发射载荷和空间高低温环境的考核，在轨顺利展开到位[16]。在月球重力作用下，“嫦娥四号”着陆器上的卷筒式伸杆机构末端的挠度约为200 mm，由此可估算其一阶频率约为0.90 Hz，与分析值基本一致。

6 结 论

1)在卷筒式伸杆机构设计过程中，在满足机构包络要求的前提下应尽可能增大弹性卷筒的末端半径并减小带宽尺寸。

2)在末端半径5～15 mm的设计区间内，比刚度随末端半径的增大而近似线性增大；一阶频率随末端半径的增大而近似按照两段不同斜率的直线规律线性增大，在7.5～15 mm区间内，增大的斜率更大。

3)弹性卷筒的一阶频率随带厚的增加近似线性增大，但比刚度随带厚的增大而近似按双曲线规律下降。

4)弹性卷筒末端螺旋角在62°～75°时，弹性卷筒的比刚度可获得最优值，其具有最高的结构效率。

5)卷筒式伸杆机构的展开刚度理论分析结果0.83 Hz与试验结果0.885 Hz之间相对误差为6.2%，表明理论分析方法有效。