飞轮微振动的组合隔振装置设计及实验研究
孙洪雨,张 雷,2,3,陈善搏,2,3,谷 松,2,3,李 季,2,3
(1. 长光卫星技术有限公司,长春 130033;2. 中国科学院长春光学精密机械与物理研究所,长春 130033;3. 中国科学院大学,北京 100049)
0 引 言
进入航天时代以来,随着军事侦查、商业探测等需求的不断提升,对光学遥感卫星分辨率和指向精度、稳定度等指标要求越来越高。然而星上飞轮等活动部件在轨工作时会不可避免地产生一定量的微小扰振,这些振动虽然不会对卫星结构造成破坏,但会导致光学载荷成像质量下降,甚至造成图像模糊、扭曲现象[1-2]。
高分辨率光学遥感卫星对飞轮微振动十分敏感,如何降低飞轮等扰动部件微振动带来的成像影响,已经变成遥感卫星研究领域的一个关键难题。目前常见解决手段是通过隔离扰振源或隔离光学相机等隔振抑制方法实现[3-4],通过合理布局隔振装置,优化隔振装置频率,改变传力路径和提高结构传递阻尼等途径达到抑制效果;隔振措施分为主动隔振、被动隔振、主被动混合隔振三种方式[5-6],其中,被动隔振装置由于易隔离高频振动,安装体积小,成本低、结构形式简单等特点,在国内外遥感卫星上被广泛使用[7]。
本文在充分调研国内外隔振方案的基础上,提出了一种新型飞轮微振动被动隔振抑制方式,从源头隔离飞轮微振动对光学相机成像质量影响,通过仿真分析与试验测试进行了组合隔振方案合理性验证。通过仿真分析预测了飞轮一次谐波、高频扰振等对像素偏移的影响,为组合隔振设计及试验测试方案设计提供有效指导;搭建了地面微振动实验测试平台,借助弹簧悬吊、信息采集等系统、积分球、平行光管等设备,进行有/无隔振装置两种状态下地面光学狭缝成像试验,精确测量出飞轮微振动引起光学系统的像素偏移,并与仿真分析进行对比校验。
1 飞轮扰振特性分析
某型号卫星在轨运行过程中,采用飞轮进行姿态控制,飞轮是星上最主要的扰振源,飞轮内部转子会持续高速旋转并产生频率成分丰富的扰振力与扰振力矩,引起卫星姿态抖动与结构振动,其扰振力/力矩是由几个原因造成的,包括转子动静不平衡、轴承制造误差和轴承刚度的非线性等[8-9]。
采用Kistler扰振测量试验平台对飞轮扰振力/力矩进行测量,试验时,依据卫星在轨成像时飞轮工作状态,将飞轮设置为转速模式,将信号采样频率设置为4096 Hz,在0~2000 r/min不同转速范围内,以100 r/min为步长,待飞轮转速稳定后采样1 min,得到飞轮扰振输出的时域数据,通过快速傅里叶变换,得到飞轮扰振数据的频域信息,某典型飞轮频域特性测试结果如图1所示。

图1 飞轮扰振力/扰振力矩瀑布图Fig.1 Waterfall map of flywheel vibration force/moment
在测试时,考虑飞轮在轨工作需求,分析截止频率设为500 Hz,由图1可知,扰振峰值主要集中在一次谐波与300 Hz以上高频处;在420~500 Hz间,径向扰振力FX及FY量级达到0.6 N,呈V字型分布,飞轮轴向扰振力FZ量级相对较大,峰值达到5 N左右,但其频率分布相对固定,主要集中在320~400 Hz间[10-11];300 Hz以上高频扰振主要由飞轮轴承的制造误差等因素引起,当轴承滚动体在存在缺陷或者磨损的表面上滚动时,轴承转动会产生频率丰富的扰振激力,当这些扰振力与飞轮结构固有模态发生耦合时,将引起扰振峰值的进一步放大;一次谐波特性在扰振力/力矩上均较为显著,为飞轮等转动机构的典型特征,主要由飞轮动静不平衡所致,在图中体现为从原点出发的一列谐波线,其幅值与转速平方成正比,幅值对应频率与转速成正比[12]。
2 无隔振状态下仿真计算
分析飞轮扰振力/扰振力矩对光学相机的成像质量影响时,需要充分考虑光学相机内部各光学元件与飞轮扰振频率发生耦合的情况[13],某星光学相机主要由主镜、次镜、三镜、焦面等光学元件组成,各元件在光学系统内相对位置如图2所示,由于飞轮微振动量级较小,造成光学元件镜面面型变化极小,所以整星有限元建模时,各光学元器件变形导致的成像质量影响忽略不计。

图2 光学系统布局图Fig.2 System layout of the optical camera

图3 卫星有限元模型Fig.3 Satellite finite element model
整星有限元模型如图3所示,其中,光学相机元件、飞轮支架等均采用三维实体单元,单机板和帆板等结构板均采用板壳单元,其余飞轮等单机设备采用质量点模拟。
在无隔振措施情况下,对飞轮施加单位力/力矩,以获得光学相机主镜、次镜、三镜、焦面等光学元件的位移与角位移输出;并将输出的位移/角位移与飞轮输入的扰振力/力矩相乘积,利用MATLAB数据处理,结合各光学元件光学放大系数,计算出飞轮微振动引起的光学相机像素偏移量。频域特性分析结果如图4所示。

图4 无隔振状态下像素偏移结果Fig.4 Simulated results of pixel offset without vibration isolation
由图4可知,在300~400 Hz间无较大峰值产生,表明飞轮的轴向扰振力FZ没有与整星固有频率发生耦合;飞轮径向扰振对光学相机成像影响最为明显,分布在420~500 Hz间,呈V字型,与飞轮输入特性曲线趋势一致,其最大像素偏移达到0.11个像素。在130 Hz低频处,产生新的共振峰,幅值达到0.034个像素,主要是由整星模态引起。其中,300~500 Hz间高频分布比较集中,对光学成像影响最大,无法满足频域上低于0.05个像素偏移的成像指标要求,需过隔振装置予以降低或消除。
3 组合隔振装置设计与仿真校验
3.1 隔振系统基本原理
不考虑陀螺效应影响,当飞轮质心与隔振装置的刚度中心相近时,隔振装置在六个方向的力传递系数与单自由度隔振系统形式完全相同[14],因此可以基于单自由度隔振系统的基本原理对隔振装置设计进行指导,单自由度隔振系统模型如图5所示。
输入激振力与隔振后传递力表达式如下:

(1)

(2)

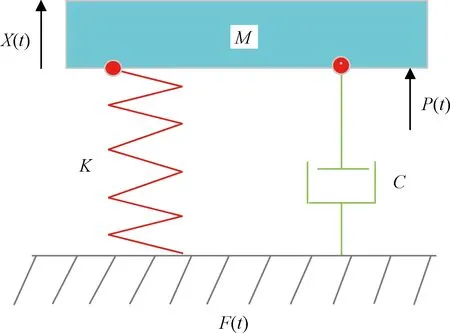
图5 隔振系统基本原理Fig.5 Basic principle of the vibration isolation system
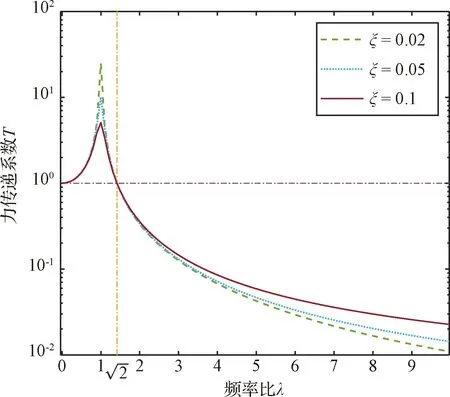
图6 隔振系统输出曲线Fig.6 The output curve of the vibration isolation system
3.2 隔振装置设计及分析
基于隔振系统基本原理,设计了一种组合隔振装置。采取不同于已往的隔振器布局方式,将隔振器布置在飞轮与飞轮支架间,在隔离飞轮扰振输入的同时,有效提高了隔振装置的隔振频率;将姿控飞轮集中布局在一个飞轮板上,在飞轮板与结构框架板间增加一层隔振装置,改变飞轮到光学相机传力路径上的阻尼和频率特性,以降低飞轮扰振的传递,两层隔振装置以组合方式获得飞轮微振动最优的隔振效果。隔振装置在星体上有严格的热控包覆及加热片等温控措施进行保护,以避免橡胶隔振性能受到温度变化影响;同时,为确保隔振装置对飞轮扰振起到全向隔振作用,要求隔振装置三向隔振频率相差不超过5 Hz;组合隔振系统结构如图7所示。

图7 组合隔振装置结构图Fig.7 Structural layout of the vibration isolation device
由隔振原理可知,隔振装置频率越低隔振效果越好,但较低频率状态下飞轮可能产生陀螺效应影响而失去控制,甚至很难保证飞轮发射段的力学性能,所以在隔振装置设计时,在满足微振动设计要求的前提下,尽量提高隔振装置的隔振频率;综合考虑卫星固有模态频率及低频状态下飞轮陀螺效应影响,对板间隔振装置要求三向固有频率均大于65 Hz;同时,为了使隔振效果更优,对扰振源飞轮增加了隔振设计,以降低飞轮扰振量级输入;由力传递系数曲线可知,为了避开与板间隔振装置频率发生耦合共振放大,飞轮隔振装置频率需不小于92 Hz才能起到隔振效果,所以本文设计飞轮隔振装置一阶固有频率为不小于100 Hz。
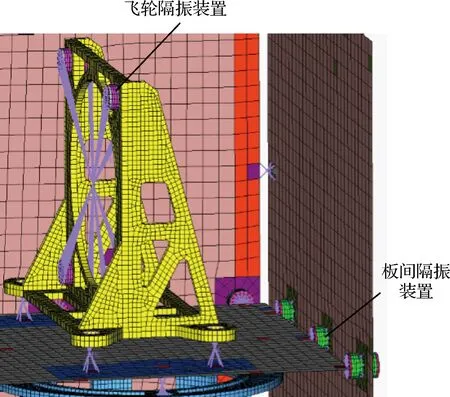
图8 组合隔振装置有限元等效模型Fig.8 Finite element equivalent model of the combined vibration isolation device
将上述组合隔振系统引入整星有限元模型中,如图8所示,对飞轮进行扰振加载,取临界阻尼为0.001,得到频域像移结果如图9所示。
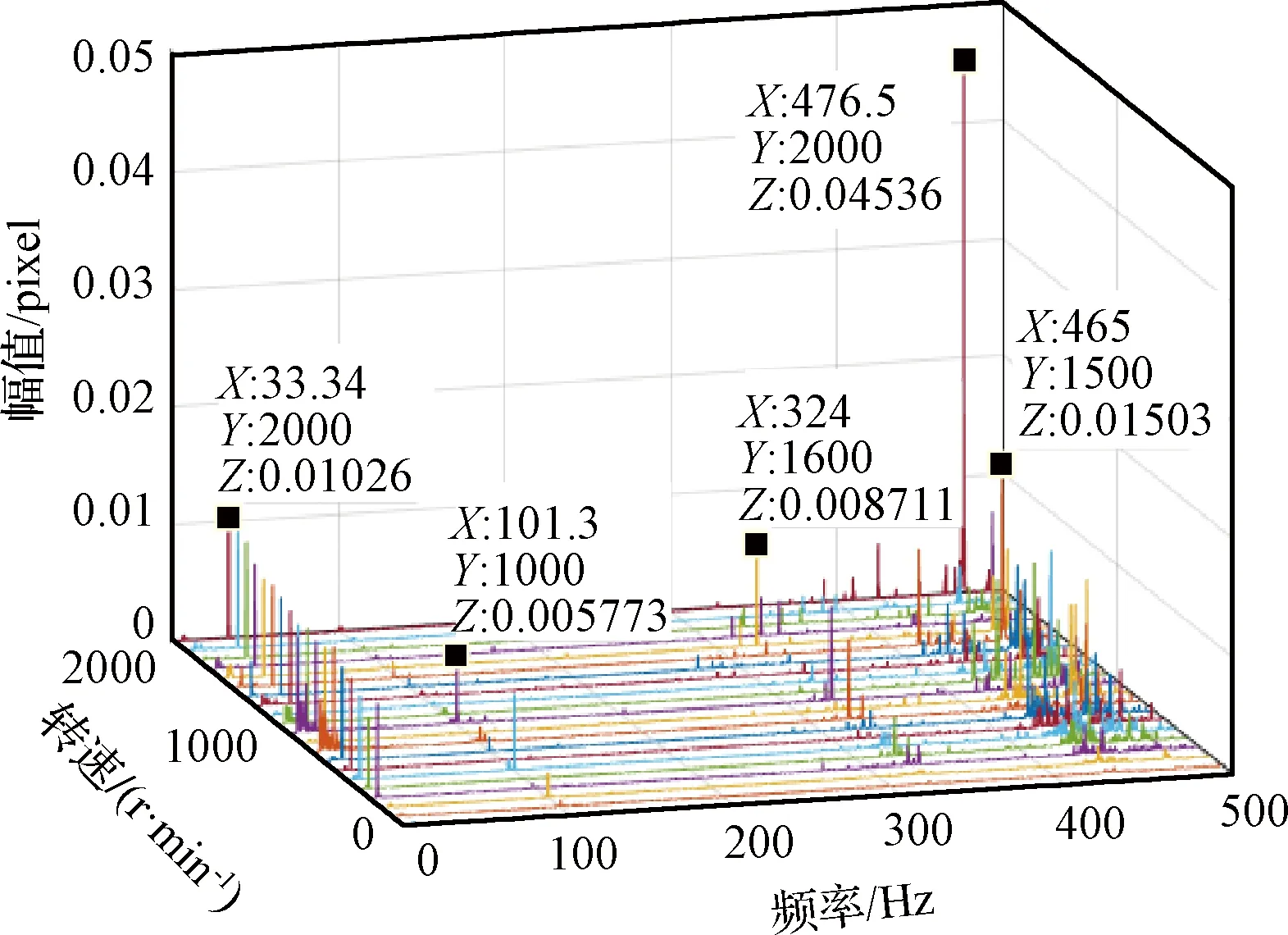
图9 组合隔振状态下像素偏移Fig.9 Simulated results of pixel offset with vibration isolation
从图9中统计数据可知,增加组合隔振装置后,飞轮高频扰振引起的最大像素偏移降到0.045个像素,与隔振前相比,隔振效率达到60%,其余最大像素偏移也均降到0.015个像素以下,表明隔振装置设计对主要由飞轮轴承制造误差等因素引起的高频扰振有较大的衰减作用;由于隔振装置频率设计在65 Hz以上,所以一次谐波峰值特性对像素偏移影响与隔振前几乎没有变化。
4 地面微振动测试实验
4.1 实验测试平台搭建
为了进一步校验隔振装置设计的合理性,本文完成了光学相机狭缝成像实验平台搭建。实验平台主要包括光学相机、弹簧悬吊系统、信号采集系统和飞轮控制系统、平行光管、狭缝靶标及积分球等,实验测试现场如图10所示。

图10 光学狭缝成像实验测试现场Fig.10 Test site of the optical slit imaging experiment
其中,弹簧悬吊系统主要是为了抵消重力对实验结果带来的影响,以模拟卫星在轨运行的失重环境;实验时,卫星翻转处于近水平状态,以方便平行光入射与狭缝靶标进行成像;飞轮控制系统对飞轮实现不同转速控制,以模拟卫星在轨真实驱动状态;信号采集系统用于光学相机焦面等成像程序的加载、测试及狭缝成像图像信号采集和处理。
4.2 实验内容及结果对比分析
实验时,为了减少环境噪声的干扰,成像数据采集均在晚上九点后进行,空调、电子学设备、机械设备等均处于关闭状态;同时为了分析图像的狭缝偏移特性,采用最大95%的设定阈值来消除环境噪声影响;然后从成像图片中提取狭缝窄线,通过均值计算求出狭缝图像的质心偏移,获得图像的时域像移数据,经过快速傅里叶变换,得到不同频率下频域像素偏移,光学狭缝成像示意如图11所示。

图11 光学狭缝成像示意图Fig.11 Schematic diagram of optical slit
在无隔振措施、组合隔振两种工况下,以100 r/min为间隔,分别对飞轮0~2000 r/min不同转速进行微振动实验,频域对比结果如图12和图13所示。
由图12~13可知,实验时,空间环境等背景噪声干扰低于0.003个像素,幅值量级相对较小,可以忽略其影响。在无隔振状态下,300 Hz以上飞轮高频扰振对光学相机像素偏移影响最为显著,最大达到0.056个像素;飞轮一次谐波等低频扰振特性对成像影响较小,最大像素偏移量低于0.01个像素,这与无隔振装置仿真计算结果趋势较为一致。采取组合隔振措施后,高频段隔振效果最为明显,在300~500 Hz间无较大峰值产生,最大像素偏移降到0.01个像素以下,隔振效率达到80%以上,表明组合隔振装置对飞轮高频段轴向扰振和径向扰振均有较大衰减作用,而在低频100 Hz以下,隔振前后飞轮扰振造成的成像质量影响变化不大,仍低于0.01个像素,这与组合隔振装置设计的初衷比较相符;由于卫星模态振动影响,在100 Hz附近产生新的扰振峰,但峰值较小,也均低于0.01个像素。
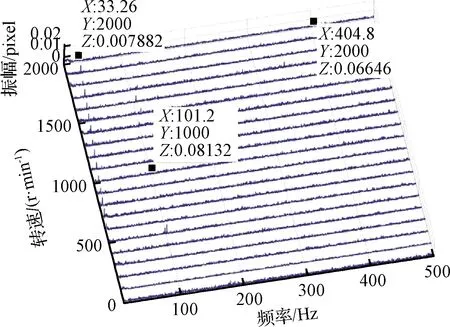
图13 组合隔振后实验测试结果Fig.13 Experimental results with combined vibration isolation device
在组合隔振后,分别对各频率段内实验测试结果与仿真分析结果进行峰值统计,其结果对比情况如表1所示。由表中数据可知,低频状态下,飞轮一次谐波、模态共振等引起振动峰值在仿真与实验测试中表现出较好的一致性;但在300~500 Hz高频段,不同于仿真分析结果,实验测试中飞轮径向扰振与轴向扰振引起的像素偏移影响被完全抑制。差别源于仿真有限元模型建立时,结构板、单机建模及连接关系等均进行了简化处理,在300 Hz以上的高频状态下,无法与实验测试装置各阶模态频率保持完全一致,造成仿真出现偏差;同时,仿真计算时临界阻尼设为0.001,而实验阻尼为随着卫星各阶模态发生变化的动态阻尼,两者无法完全等效;后续将结合实验结果及在轨验证数据对仿真模型进行进一步修正。

表1 各频率内实验测试结果与仿真分析结果峰值统计Table 1 Peak statistics of test results and simulation analysis results at different frequencies
5 结 论
从飞轮输入特性频谱分析结果可知,飞轮的扰振主要集中在一次谐波和300~500 Hz间高频段,其中,330 Hz轴向扰振力振幅最为显著;通过无隔振措施有限元计算,结果表明,由飞轮径向扰振引起的像素偏移最大达到0.11个像素,无法满足光学成像指标要求;分别在飞轮与飞轮支架间,飞轮板与结构框架板间进行了隔振装置设计,采用组合隔振方案后,仿真结果显示:高频段微振动响应得到极大衰减,最大像素偏移降到0.045个像素,隔振效率达到60%;通过微振动光学狭缝实验测试,结果表明:隔振后,300 Hz以上的高频响应被有效抑制,最大像素偏移降到0.01个像素以下,峰值隔振效率达到80%以上,证明了隔振方案设计的有效性;由于仿真模型的简化与阻尼设定不同于实验测试,300 Hz以上高频段仿真计算结果与实验测试结果表现出一定偏差,后续将对仿真模型完成进一步修正。
本文设计的组合隔振装置不同于以往的飞轮隔振方式,创新采用了新组合隔振模式,目前已在某型号卫星上成功应用,为遥感卫星微振动抑制技术提供一种新的有效方式与解决途径。

