解析一道高三数学试题

江苏 郑宝生 潘 鑫

随着时代的发展，每年的高三都会有一些新颖的试题出现，有些题目人为编造的痕迹太重，但有些题目却让人赏心悦目，用怎样的标准来评判试题的优劣？有许多问题值得我们思考．下面的题目是2019年无锡市高三数学期中考试第17题(改编)，试图通过对本题的研究来解答我们的疑虑.

一、题目

(Ⅰ)若∠BAC=60°,求sinBsinC的值；

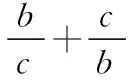
二、题目的背景

本题涉及的知识点，有初中的直角三角形的边角关系和勾股定理，高中解三角形的正、余弦定理，还有三角函数及三角恒等变换等，关键在于这些知识点的融会贯通．首先，正、余弦定理的应用灵活且广泛，三角恒等变换也是变化万千，三角函数又是最典型的周期函数，它们在建立数学模型解决实际问题中，有着举足轻重的作用．其次，它考查了学生对正、余弦定理的熟练运用，体现了数学变换的方向，以及三角函数模型的建立．最后，对于高三学生来说，他们已经进入了高中数学的一轮复习，解三角形和三角函数已经复习完成，对于三角函数里简单的问题还是能够处理的，此时学生更缺乏解题经验的积累、对问题深入的思考以及思想观念的提升，一些综合的、新颖的问题仍然会使他们束手无策.

三、题目的来源

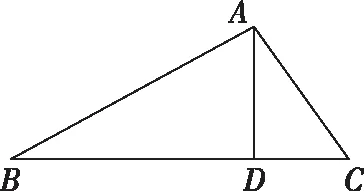
四、题目的解法

本题第一问有多种不同解法，主要是利用直角三角形的边角关系，正、余弦定理以及三角形面积公式等.

1．利用正弦公式

2．利用余弦公式

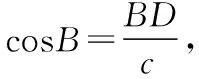
3．利用正切公式

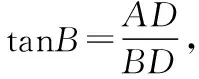
4．利用余弦定理

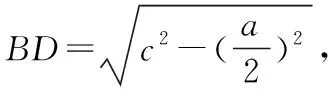
5．利用三角形外接圆半径

6．利用三角形的面积公式

五、题目的本质

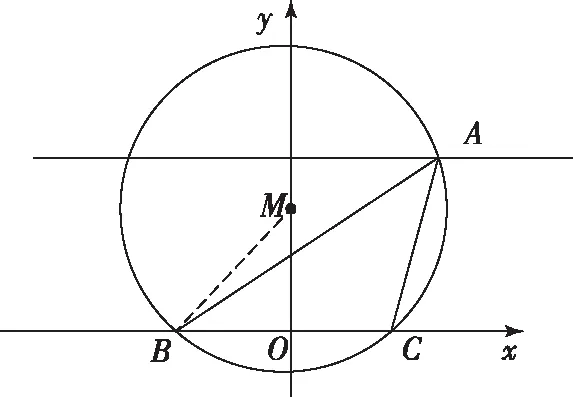
六、题目的变式

七、题目的一般化

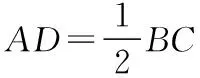
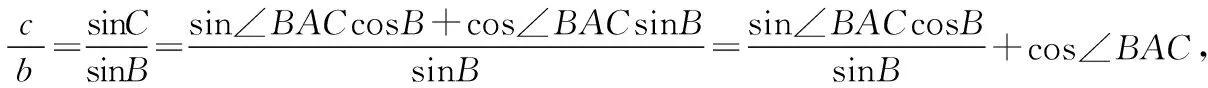
八、解题的思想方法

九、题目的价值

十、题目链接

本问题是通过列方程的方法，寻找题目中隐含的等式，然后再通过这个等式去求解其他问题，与此类似的高考试题如下：

1．(2016·江苏卷·14)在锐角三角形ABC中，若sinA=2sinBsinC,则tanAtanBtanC的最小值是________.

由于sin(B+C)=2sinBsinC,所以sinBcosC+sinCcosB=2sinBsinC，则tanB+tanC=2tanBtanC，再用这个隐含的等式去求解.

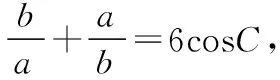
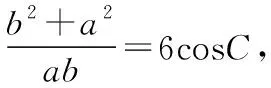
(Ⅰ)求sinBsinC；

(Ⅱ)若6cosBcosC=1，a=3，求△ABC的周长.

所以好的试题从形式上看，简洁优美；从内容上看，内涵丰富联系广泛；从问题的角度看，能发人深省；从知识的角度看，能体现数学的本质.