核心素养视域下小学数学模型思想的培养

石丽敏

（福建幼儿师范高等专科学校，福建 福州 350007）

在新时代背景下，我国正在向全面深入推进课程改革的新阶段发展。毫无疑问，核心素养视域下的基础教育教学改革是发展的必然趋势。虽然小学阶段的数学核心素养还未正式提出，但也离不开义务教育数学课程标准中涉及到的数学十大核心概念。例如，高中的数学抽象素养在义务教育阶段主要表现为数感和符号意识，逻辑推理即推理能力，直观想象即表现为几何直观和空间观念，而模型思想则是对应数学建模素养。［1］因此，建立并初步形成模型思想将有助于小学生提升数学核心素养。

数学模型是指用数学的语言和方法来描述现实对象数量规律的一种数学结构。也就是说，数学模型构建了数学与外部世界的桥梁。在小学阶段，数学概念、公式、数量关系、图形和图表等都可以看作是数学模型，而模型思想的形成正是蕴含在建立和求解这些数学模型的过程当中。可以看出，模型思想的培养应重点突出如何用知识和方法建立模型，以及如何用模型来解决实际生活中的问题。在这个过程中，可以逐步帮助学生感悟数学与现实的联系，增强应用意识和创新能力。下面笔者将分析模型思想培养所要遵循的原则，并在此基础上提出培养策略，以期为小学阶段模型思想的培育提供新思路。

一、小学数学模型思想的培养原则

（一）自觉性原则

在数学教材中，关于数学概念、定理和运算法则等知识都有着具体的表述。而模型思想作为一种思想方法，它则是散落在教材的各个章节，隐藏在数学的知识体系里，教师在教学过程中往往会忽略模型思想的培养，或者受到教学时长的限制将它作为一个“软任务”挤掉。这就需要教师首先从观念上进行革新，在思想方面加强对其重要性的认识，在备课环节有意识地把数学模型思想作为教学对象，把表层的数学知识和渗透数学思想方法同时纳入教学目的，这样才能达到培养模型思想的要求。

（二）渗透性原则

由于模型思想是蕴含在数学知识的形成、发展和应用当中的，对于它的教学会比教授一般的数学知识困难。因此，教师需要对教材进行深度研究，挖掘每个章节背后可以进行模型思想渗透的各种因素。还应考虑如何结合具体内容进行渗透，渗透到什么程度，形成一个总体的方案［2］。通过这种逐步渗透的方式，渐渐加深学生对于模型思想的认识。

而强调渗透性并不等同于不能直接点明思想方法，还应根据不同阶段学生的特征，采取针对性的渗透方式。比如，在理解掌握思想方法的明朗化阶段，学生在运用模型思想解决数学问题上已经积累了一定程度的经验，此时隐藏在数学知识背后的模型思想就会逐渐显露出来，引发学生的注意并使其产生某种程度的领悟。这时候教师便可直接介绍和点明模型思想，要求学生掌握运用解决数学问题的思路和方法。

（三）参与性原则

对于数学模型思想的培养，需要学生在经历建立和求解模型的过程当中逐步形成，这也是《义务教育数学课程标准（2011 年版）》中对模型思想的基本要求。在教学过程中，教师应创设能够吸引学生的问题情境，同时扮演好引导者的角色，让学生积极参与到问题的抽象、模型的建立、求解及检验的数学活动中来，自主探索模型思想的真谛，从而初步形成模型思想，继而培养其应用意识和数学语言的运用能力。

二、小学数学模型思想的培养策略

依据模型思想的培养原则，针对模型思想形成的规律和过程，提出以下几点培养策略。

（一）立足教材，深度挖掘模型思想

在小学数学教材中，学生模型思想的形成应广泛蕴涵于“数与代数”“图形与几何”“统计与概率”等教学内容之中。例如“数与代数”领域中涉及到的一些数的概念、性质、常见的数量关系以及运算的程序等；“图形与几何”领域中涉及到的一些图形的概念、特性和周长、面积、体积公式等；“统计与概率”领域中涉及到的分类整理、数据收集整理、条形统计图等基本模型，这些内容的教学都是模型化思想渗透的重要途径。［3］

因此，这就需要教师深入挖掘教材中能够进行模型思想渗透的各种因素，并结合具体内容形成完整的授课方案，逐步发展学生的数学素养。

（二）明确要求，分层渗透模型思想

模型思想作为一种思想方法，要使学生真正有所感悟并非一朝一夕就能完成的，需要经历一个长期的过程。在这个过程中，学生对于隐藏在知识后面的模型思想是从未能引起注意到产生某种程度的领悟。当积累一定程度的经验后，模型思想便会凸显出来，最后逐步形成运用模型进行数学思考的习惯。因此，这就需要教师结合学生身心发展的特点以及不同学段的学习要求，分层渗透模型思想。

例如，在第一学段，学生刚刚接触模型思想，因此这一阶段主要是以积累数学活动经验为主。如低年级的教师在讲授“认识图形（平面）”时，可以事先准备一些立体积木，引导学生通过描、画、印等多种方法把这些立体图形的面留在白纸上，使学生体验从实物抽象出平面图形的过程，以此形成各种平面图形在头脑中的模型表象。最后还可以让学生找一找在生活中还有哪些物体的面是刚刚学习过的平面图形，以赋予这些图形更多的“模型”意义，初步渗透模型思想。

随着运用模型思想解决问题的实践经验增多，在第二学段便可通过创设具体的问题情境，引导学生通过动手操作和观察比较抽象概括出更为一般的数学模型。如四年级下册“三角形定义”的教学，教师首先可以创设包含三角形的生活情境图引出学习主题，而后提出“画一个三角形”的要求，引导学生观察比较所画的各种三角形的边、角和顶点的位置关系，并尝试用自己的话来概括三角形的定义。在此过程中，教师应帮助学生不断完善用词的准确性，如“围成”与“组成”的不同，最后共同归纳总结出三角形概念的模型。更进一步，引导学生学会用字母A、B、C 分别表示三角形的三个顶点，由此三角形可表示为三角形ABC。

总的来说，模型思想的渗透需要考虑到不同年龄段的学生水平，要求第二学段的学生能够在前期积累的实践经验上，通过多次应用模型思想进行探索和思考，逐步加深对模型思想的理解，最终达到运用自如的程度。

（三）重视应用，开展数学建模活动

课程标准中对于建立和求解数学模型的过程可以概括为“问题情境—建立模型—求解验证”这三个步骤，开展这一系列的教学活动能够使学生对于模型思想有着更深层次的体会，真正感受到数学模型与实际生活的联系。教师在开展活动的过程中要注意扮演好引导者的角色，启发学生自主思考，促进相互间的交流探讨，让学生在经历模型的构思、建立以及求解检验中逐步树立应用意识，积累解决实际问题的经验，从而感悟模型思想的本质。

例如，人教版五年级上册《植树问题》

1.问题情境

教师展示实际问题情境“要在全长为20m 的小路一边植树，每隔5m 栽一棵”，请学生思考植树的方案并尝试通过画图表示出来。预设学生会画出以下三种情形：

2.建立模型

追问1：上述三种情形有什么相同之处呢？

教法：引导学生观察比较这三种线段图，分析总结出三种情形都将线段分成了4 段的结论。在此基础上，启发学生从线段总长、间距和间隔数之间的关系入手，归纳出计算间隔数的模型，即间隔数=总长÷间距。

追问2：如果在这条全长为20m 的小路上每隔2m、4m 或10m 栽种一棵树，你还能计算出这几种情况分别对应的间隔数吗？请大家在作业纸上画出线段图并尝试完成表1 的填写。

表1

教师引导：你们有没有发现两端都种、两端都不种和只种一端这三种情形下的棵树与间隔数之间存在着某种联系？

教法：组织学生分小组讨论这三种情形下棵树的计算规律并进行汇报，在此基础上教师总结规律：当两端都种时，棵树=间隔数+1；当两端都不种时，棵树=间隔数-1；当只种一端时，棵树=间隔数。

3.求解验证

教师引导：接下来大家可以在作业纸上画一画，试着利用直观图来描述棵树与间隔数的对应关系。

教法：在学生尝试的基础上，教师借助直观图（如图1）进一步解释和验证上述规律。

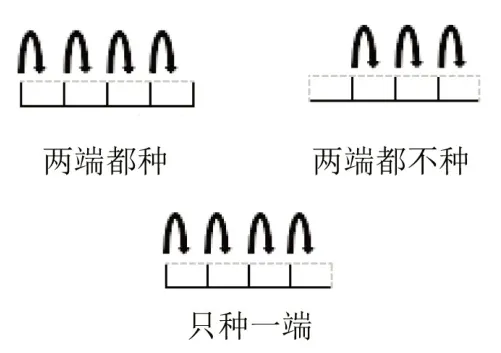
图1

三、总结

模型思想是需要学生在经历从实际背景中抽象出数学问题、构建数学模型和寻求结果的过程中形成的，传统的以知识为导向的教学方式往往只关注学生知识点的达成，却忽视了思想方法的渗透，导致学生无法真正感悟模型思想，更加不利于培养学生的数学核心素养。因此，应当重新思考模型思想的培养方式，即在遵循自觉性原则、渗透性原则和参与性原则的基础上，通过深度挖掘模型思想、分层渗透模型思想以及开展数学建模活动的方式逐步培养学生的模型思想，促进数学核心素养的形成。