“一转、二变、三译、双基本”——初中几何入门教学策略研究

尤庆林

（福州三中罗源校区，福建 福州 350600）

促进学生思维的发展是数学教学的终极目标。初中几何教学是通过几何直观的数学思维训练启迪和发展学生思维，将知识发生、发展过程与学生学习知识的心理活动统一起来。初中数学知识由具体转为抽象，从文字转为符号与图形。在一定程度上导致学生由“数”转入“形”，难适应；论证推理逻辑性强，难入手。具体表现在：对几何学习缺乏兴趣，不善于联系生活实际; 不善于根据题意分析探索解题途径;对几何语言的理解、运用不透彻;不会正确画出合乎要求的几何图形，不会写出合乎逻辑的解题过程；缺乏从复杂图形的分解中，找出“基本图形”的能力。针对以上问题，笔者在平时教学过程中注重学习方法的引导，通过操作实验、基本技能的训练等活动，在具体概念教学中创设情境让学生在学习中感受几何学习的乐趣。现结合多年的教学经验，就提高初中几何入门教学的有效性谈几点思考。

一、创设几何概念、定理形成的现实情景，化概念为具体

初中学生刚接触几何，在心理上需要适应，这个时候教师应该引导学生从学概念和定理入手。几何概念较为抽象，在进行概念或定理教学时，首先，尽量从实例、模型建构入手，通过分析图形的相关特征得出几何概念及图形性质，用文字把概念描述出来。如教师在讲“角”的概念时，可先引导学生观察圆规的两脚张开后所形成的形状及钟表上时针与分针所构成的形状，进而归纳出“角”的定义。一些容易发生错误的概念可以通过反向变式来纠正。（如图1，2）

图1

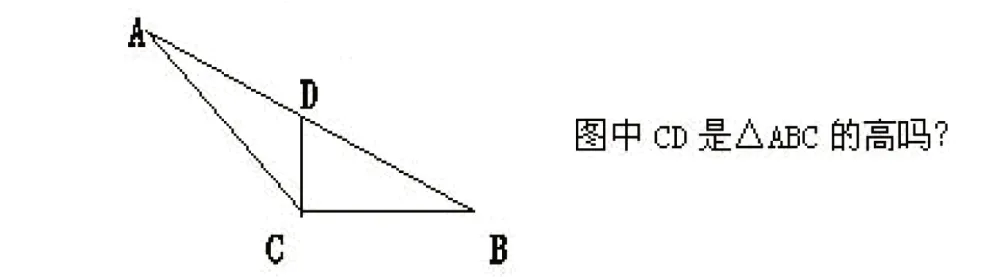
图2

其次，结合图形，创设情境，更好理解定理。为了学生能够更好地理解和接受抽象的内容，掌握解题方法，教师可以充分借助几何直观、几何解释。例如：证明全等三角形不能用“SSA”的问题，教师不仅要按教材给予说明，还要举出对应的实例，加深学生的理解。最后，学生在论述概念定理时，对学生在概念定理认识上的错误要及时发现并纠正。通过不断强化严密的逻辑思维能力，养成认真推敲，逐句分析的良好习惯。如教师在讲解“等边对等角”这一定理时，要把该定理拓展为“三角形中相等的边所对的角相等”，还要说明“边”与“角”的相对关系。

二、引导学生操作实验，实现抽象到具体的转化

在课堂教学中，为了能够帮助学生更好地理解抽象的几何知识，可以通过让学生亲自观察、动手操作等方法获取几何图形的相关知识，培养学生观察和动手能力。这是几何教学的重要组成部分。学生通过动手操作可以加深对数学知识的理解，提高合作交流、自主探索的能力。

（一）拼中学

在学习全等三角形的“SSS”时，课上教师可以给出三角形的三条边，让学生按照规定的长度画出三角形，然后把它裁剪下来（课前交待学生准备好学习材料、工具），小组间比较各自裁剪下来的三角形大小、形状，看看是否会重合，从而总结出“SSS”。教师在教学过程中要多从生活中寻找让学生感兴趣的生活原型，挖掘教材内容的实质，使两者有效的结合，通过理论联系实际把抽象的几何知识转化为直观表象，降低学生的学习难度，激发学生的求知欲。

（二）折中学

一把剪刀，几张纸片，生活中随处可见的简单工具包含丰富的内涵。通过简单的图形折叠，有利于培养学生的空间想象能力与动手能力，实践能力与创新能力。图形的折叠实质就是翻折与对称变换，很好地体现了数学解法的灵活性、开放性。在特定的几何教学中，教师利用图形的折叠，能很好突破教学的难点。如在讲解等腰三角形的性质时，为了让学生能够较快地发现等腰三角形是轴对称图形和掌握等腰三角形“三线重合”定理，教师在课堂上可以让学生剪出一个等腰三角形，并使两腰折叠重合。在折叠过程中，提醒学生注意观察折痕两旁的图形是否重合，通过这种方式能容易得到结论。同时，它的折痕对指导等腰三角形性质的证明有启发作用。

三、重视基本技能的训练，夯实几何证明的基础

课堂上，教师在讲析证明题时可以适当对讲解内容进行分拆，以培养学生的看图方面的能力。如图3，E 在AC 上，D 在AB 上，∠B=∠C，AB=AC.求证：AE=AD.

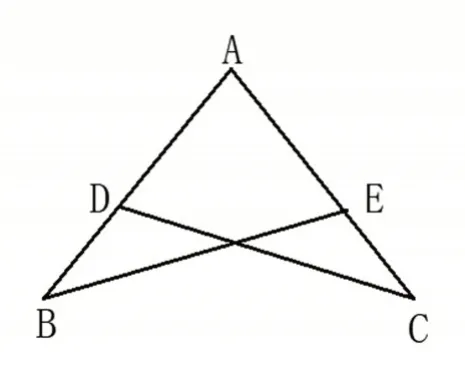
图3

［分析］AE 和AD 分别在△AEB 和△ADC 中，所以要证AE=AD，只需证明△AEB≌△ADC 即可。

证明：在△AEB 和△ADC 中

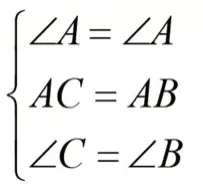
所以△AEB≌△ADC（ASA）

所以AE=AD.

讲解时，将图形分拆成△AEB 和△ADC，通过提问的方式让学生思考：“两个三角形怎么运动才能相互重合”，可以培养学生将复杂图形分解成各种简单图形的能力，以及空间想象能力和逻辑推理能力。而让学生找出两个三角形对应边和角，找出图形中的不同的元素，以及每个元素之间的对应关系，则有利于培养学生的数学观察能力。

在教学过程中充分运用一图多变，分层递进的教学方式，要关注到不同知识基础的学生，充分考虑课堂提问、例题、课堂练习选择等各个环节的设计层次性。比如，为了让学生更直观地认识轴对称变换，在学习轴对称变换时，教材中通常把对称轴画成铅垂线，按照教材的内容，对称点之间的连线就是水平线。在教学过程中如果教师不刻意提醒，有一部分学生在对称点的位置上会认为它们一定在水平位置上，在解决问题的时候就会出现如右图的错误，就会产生知识负迁移。因此教师在上课时，除了讲清对称点的画法外，更应该在教学中采用“一图多变”进行强化训练，更好地达到预期的教学效果。例如：以直线m 为对称轴，做出下列图形的轴对称图形。（如图4）

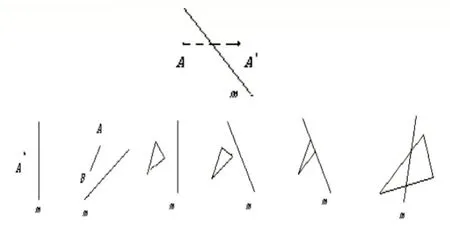
图4

通过如上操作：由画对称点到画对称线段最后画出对称图形，由易到难，层层递进，既满足不同层次学生学习的需求，提高了他们学习几何的自信心。也为更好抓住轴对称的本质特征，更深刻理解轴对称的概念，提供了有效的课堂支撑，对培养学生学习几何的兴趣起到了一定的作用。

四、加强“文字语言”和“数学语言”的“互译”训练,增强几何运用能力

初中学生几何形象思维能力水平较弱，具体表现为虽然能够背熟定义、定理，却不会将定义、定理转化成相应的数学语言，不会识别几何图形、更难准确地画出几何图形，经常出现文字表述与图形表述脱节的情况。这在几何概念的教学中表现尤为突出。

针对以上情况，在教学时，要求学生根据几何概念的图形特征，准确地画出图形；培养学生通过描述概念的文字语言，结合图形，把相关概念翻译成配有图形的字母符号的语言能力。在平时的练习过程中即使涉及到辅助线的添法，也要重视文字语言和符号语言是否吻合。教师在平时几何概念教学中，可以让学生把所学的定理翻译成字母符号语言。如：“平行线分线段成比例定理在三角形中的应用：平行于三角形一边的直线截三角形另外两条边，所得到的对应线段是成比例线段。”结合图形写出字母符号语言（如图5）

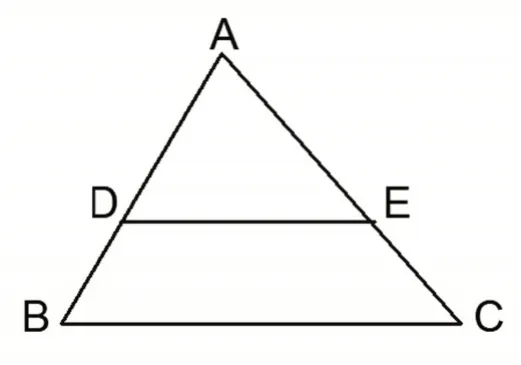
图5

如图已知，在△ABC 中，

这种“文字语言”和“数学语言”的“互译”训练,能够让学生更深刻地理解几何概念，最终达到灵活应用的教学目标，为几何学习、推理打下坚实的基础。

综上所述，我们的教学需要立足于教材，同时不能拘泥于教材。要深入理解教材中的每个设计意图，挖掘教材中的素材，提升学生空间概念。在平时教学中，教师要创造性地使用素材，提升学生的空间概念，进而提高他们的数学素养。