规整填料上传质现象的CFD模拟研究综述
刘宁馨 洪伟荣 郭雅琼
(浙江大学能源工程学院)
规整填料因具有耐腐蚀、效率高、压降低及通量大等优点被广泛应用于气液两相精馏、吸收等分离过程,在工业分离领域具有重要地位。 受困于规整填料的复杂结构和庞大计算域,CFD技术成为研究规整填料上流体力学行为的一种便捷有效的方式[1,2]。 Amini Y和Nasr Esfahany M对填料塔上的CFD流动进行总结, 归纳了现有的数值模拟研究中有关干湿压降、持液量和接触面积的结论[3]。近年来,规整填料上的流动特性已经得到了深度探索, 而传质研究正处在初步发展阶段。 现阶段,实验研究、理论与经验结合、理论与半经验结合这3种传质研究方法主要依托于具体实验,不能脱离具体的物系,导致这些方法应用有限、无法推广,因而传质研究也开始采用CFD技术。CFD模拟结果可以显示两相流体的所有信息,包括液相各个位置的厚度、压力、两相接触面积及浓度分布等,可为传质研究提供新的信息。
Fourati M等对整塔填料进行几何分解,发现规整填料板上的流动可简化为倾斜平板或波纹板上的两相薄膜流动[4]。 根据几何模型尺寸从小到大的规则, 模拟研究依次可分为微观研究、介观研究和宏观研究。 其中,微观研究的特征尺度在毫米级别,几何模型一般为表面光滑的倾斜平板或波纹板[5],模型简单,计算量较小,模拟结果可以反映主要流道上的传质情况,但其几何模型经过了简化,能反映的传质现象有限。 介观研究的特征尺寸在厘米级别,几何模型一般为规整填料中的重复性几何单元(REU),更加接近真实的填料结构[6],可以在减少计算量的情况下反映规整填料上的真实传质现象,但模拟结果只是稳定发展后的局部信息, 无法得到整塔内的进出口、壁面等位置的传质信息。 宏观研究以整个规整填料塔或多个填料层作为研究对象, 一般分为两类:一类是多孔介质模型[7],将整个填料塔流体域看作具有一定空隙率的连续介质,填料对流体的形体阻力通过动量方程模型修正项来体现规整填料结构的复杂性,不考虑规整填料的具体几何结构, 模拟结果只是填料塔内的宏观平均性质;另一类直接对填料间的流体域进行求解[8],必须考虑规整填料的具体几何形状,可以得到局部流动的具体信息,对规整填料的设计和发展具有重要意义,但需要相当大的计算资源,只能选取几个填料层的组合进行模拟计算。 为了综合各尺度研究的优势,Raynal L和Royon-Lebeaud A提出了多尺度研究方法, 将宏观和微观研究相结合,先进行计算量较小的微观模拟研究来获取一些流场信息,再将这些信息应用到宏观整体平均模型中,在一定计算量内得到尽量多的流场信息[2]。
笔者归纳了应用CFD技术进行规整填料传质特性模拟研究的现状, 主要包括传质现象的CFD数值模拟以及现有的模拟研究中有关传质速率特性的结论。
1 数值模型
现阶段大多数学者将规整填料板上的传质问题视为气液两相传质问题,不仅涉及相界面捕捉、动量方程的附加源项处理,还需要加入浓度方程。
1.1 相界面捕捉
多相流相界面捕捉方法包括Front Tracking、Level Set及Volume-of-Fluid(VOF)等。 其中,Front Tracking方法采用拉格朗日法对相界面进行显示追踪,可得到精确的界面位置[9]。 Level Set方法在整个计算区域内构造某种Level Set函数ψ,ψ函数的零值点即为两相流体的交界面,相界面的位置通过求解ψ函数进行更新[10]。为了确保ψ函数的零点在任意时刻均为相界面,ψ函数应该符合运输方程,即:

其中,t为时间项,U为速度项。
VOF模型对相界面的捕捉主要依靠相体积分数α,相体积分数的控制方程为运输方程,即[11]:

对于离散后的网格单元, 若液相充满网格,则α=1;若气相充满网格,则α=0;若网格单元内气液两相混合,则α的值介于0和1之间,此网格就为相界面。 3种多相流相界面捕捉方法的优缺点列于表1。

表1 3种多相流相界面捕捉方法的优缺点
VOF和Level Set的主要变量均满足运输方程,而且这两种方法的优缺点十分互补。 近年来,一些学者提出了一种将VOF和Level Set相结合的相界面追踪方法——CLSVOF[12]。 这种方法利用VOF的重构方法来追踪界面, 并对Level Set函数进行重初始化, 再利用Level Set方法求解界面的法线方向和曲率半径,这既可以处理界面拓扑结构的变化, 也可以准确获得相界面处的曲率、表面张力等。 后来,众多学者进一步提出了CLSVOF的优化方法,如S-CLSVOF、VOSET等。
1.2 连续性方程及动量方程
一般将规整填料上的气液两相均视为不可压缩牛顿流体,其连续性方程及动量方程如下:

其中,ρ为流体总密度,ρL为液相密度,ρG为气相密度,p为压力,g为重力加速度,μ为流体粘度,μL为液相粘度,μG为气相粘度,F为外加源项力。
填料板上流动的特征尺寸较小,气液相界面的曲率半径很小,因而表面张力不能忽略。 此外,表面张力对流体运动的重要性由3个无量纲数来定量判断,即:
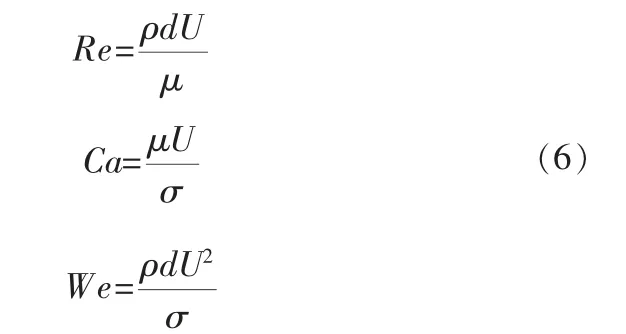
其中,d为规整填料的特征长度,σ为液相表面张力。当Re≪1时,Ca数可以衡量表面张力对流体流动的影响,当Ca≫1时,表面张力不可忽略;当Re≫1时,则采用We数衡量表面张力对流体流动的影响,当We≫1时,表面张力不可忽略。 d在REU中的具体计算式为[13]:

其中,β为波纹夹角,e为波纹板厚度,a为波纹斜边长。 在二维平板或波纹板、三维倾斜平板上时, 规整填料的特征长度d多与薄膜厚度相同或是薄膜厚度的4倍[14]。
表面张力可分解为垂直于相界面的力和平行于相界面的力。 其中,垂直于相界面的力通过表面张力源项fSV来表示,规整填料两相传质现象的模拟研究均加入了表面张力源项fSV,同时采用CSF模型, 将相界面处的压力插值为相间压力的连续函数。 平行于相界面的力通常会引发Marangoni效应。朱明将Marangoni效应源项加入动量源项, 模拟结果表明在进出口浓度相差较大时,会出现Marangoni对流,显著促进传质效果[15]。然而Marangoni效应源项较为复杂,只有较少学者将它加入源项。
除了考虑表面张力的影响,孙博还添加了气液相界面剪应力源项[16]。 通常认为在载点以下的操作范围内,气液相间的作用力对液相流动的影响很小,可忽略不计。
1.3 湍流模型
当流体速度不断增大时,填料塔内可能会产生流型变化,对于可能出现的湍流现象,主要聚焦于两个问题: 一是湍流临界点雷诺数的确定,二是湍流模型的选取。
对于湍流临界点雷诺数的确定,Zogg M提出了规整填料内流动临界雷诺数Recritical的计算式[17]:

其中,θ为填料波纹与竖直方向的夹角,ε为填料的孔隙率。
为了比较不同湍流模型对传质模拟的影响,Nikou M R K 和Ehsani M R分 别 采 用k-ε 模 型、RNG k-ε模型、k-ω模型和BSL模型对FlexipacIY型规整填料内的传质现象进行模拟研究,对比模拟结果与实验结果,发现k-ω模型和BSL模型与实验结果更为接近,误差在8%左右[18]。 Saleh A R等分别采用标准k-ε模型、k-ω模型、RNG k-ε模型和BSL模型对MellapakPlus 752.Y型规整填料进行三维REU模拟, 将模拟结果与实验数据进行比较,同样发现BSL模型与实验数据最为接近[19]。因此,采用BSL模型可以得到更为准确的模拟结果。
1.4 浓度方程
摩尔分率ck,j表示某一相k中参与质量传递的物质j的浓度,其运输方程可表示为:

其中,Dk为物质的扩散系数,Rk,j为k相中物质j发生化学反应而引起的相间物质传递。 当k为液相(L)或者气相(G)时,式(9)变为两相的浓度运输方程,这一模型称之为双流体模型[20]。
除了用双流体模型进行传质求解外,也有学者将双流体模型在整个求解域内用同一个方程表示, 提出类似于VOF的物理量定义来实现流体界面质量传递连续性的传质模型,称为连续质量传递模型[21]。 该模型中对浓度C的定义与VOF中的速度定义一致,即:

扩散系数可采用算术平均或调和平均,合并后得到浓度运输方程如下:
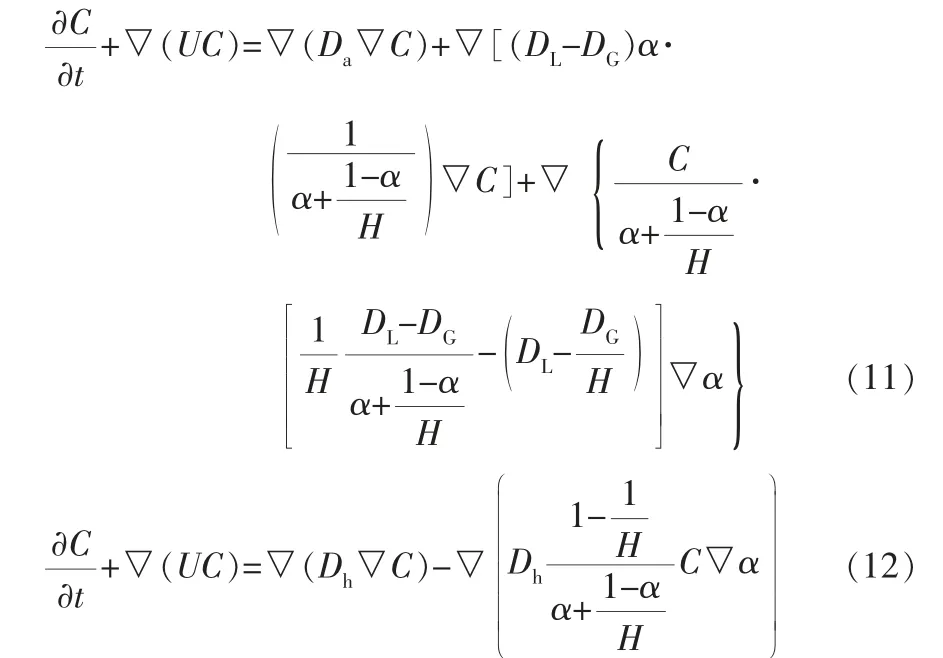
其中,Da为两相扩散系数的算术平均,H为亨利常数,Dh为两相扩散系数的调和平均。
Deising D等[11]和Haroun Y等[22]分别采用式(11)、(12) 对一维纯扩散问题进行数值模拟,并将模拟结果与解析解对比,发现两种模型的计算结果十分接近。 通过以上验证,两种模型可被认为能准确描述两相传质现象。
采用Excel 2007和SPSS17.0对数据进行处理与统计分析,用单因素方差分析比较处理间的差异性。
2 传质模拟研究
2.1 整场传质研究
规整填料上的整场浓度分布与速度分布密切相关。 Chen J B等对两块交错90°的Mellapak 350Y规整填料上的异丁烷解吸过程进行模拟,发现在气液相界面波动较强和气液相界面周长较大的位置处,传质速率较大[23]。 张西雷等对JKB-250Y金属孔板波纹填料分解后的最小单元体进行模拟分析,发现速度场与传质系数场的分布基本一致,旋涡的存在会加强传质[24]。
有学者进一步探究了流场物理量与传质速率之间的关系。 Hu J等对二维竖直平板上层流状态下的物理性吸收进行数值模拟,发现气液交界面处的涡量大小控制着浓度分布,两者相关系数平均值为0.72,涡量和浓度高度相关[25]。此外,Xu Z F等认为传质现象与气液交界面处速度波动值的垂直分量梯度η直接相关, 整场平均传质系数与η0.5成正比关系[26]。 也有学者指出,浓度场与速度场之间的紧密联系是有条件的。 Haroun Y等研究认为当扩散厚度比较小时,交界面处的传质由对流控制,浓度场分布与速度场紧密相关,符合渗透理论;当扩散厚度较大时,传质由扩散控制[27]。
所以,传质速率在整场并非均一分布,存在局部增强区。 此外,传质与流动现象紧密相关,但现在还未推导出公认的涉及流动影响传质的确定参数。
2.2 物性参数对传质的影响
不少学者探究了物性参数对传质的影响,主要涉及液相粘度、液相接触角及溶液浓度等。
Sebastia-Saez D等进行物理性吸收模拟研究,讨论了液相粘度对三维平板上传质效率的影响,结果认为液相粘度可以改变扩散系数,随着粘度的增大,扩 散系 数 减小,传质 速率 变小[28,29]。 而Singh M P和Singh R K则认为液相粘度的增大意味着表面张力的减小, 因而气液接触面积增大,传质速率增大[30]。 可见,液相粘度对传质速率的影响还需要进一步研究。
对于液相接触角对传质的影响,Sebastia-Saez D和Gu S发现当接触角小于90°时,不同接触角下传质速率相差不大,但当接触角大于90°时,气液相接触面积变小,传质速率突然变小[28]。
对于溶液浓度对传质的影响,谷芳等认为液相进口浓度越大,相间传质推动力越大,因而平均传质系数也越大[31]。Sebastia-Saez D等对三维倾斜平板上CO2被胺基溶液化学性吸收过程进行模拟, 认为胺基溶液浓度的增大导致了粘度的增大,使得CO2在液相中的扩散系数变小,因而传质系数变小[29]。 虽然研究体系略有差异,但谷芳等还进行了实验验证,因而得到的正相关结论更有信服力。
2.3 操作条件对传质的影响
Sebastia-Saez D等在倾斜平板上进行了两相传质模拟研究,认为气相压力主要是通过改变气相在液相中的溶解度来影响传质[20]。 在水-氧气这一实例中,气相压力增大则氧气在水中溶解度增大,因此传质速率有所提高。
Dong B等发现为液相控制反应时,液相传质系数与气速无关[32]。 但也有研究者表明气速对传质有影响,谷芳等[31]对二维平板以及Chen J B等[23]对REU上的解吸过程进行了模拟研究,认为气相流量增加, 两相间的湍动增强从而传质加强。 而Sebastia-Saez D等研究表明,气速增大会阻碍液相发展,减少气液相接触时间,降低传质速率[20,28]。综上可以看出,气相在两相传质中的作用并不单一,还需进一步探究。
许多学者探究了液相载荷对传质的影响。Haelssig J B等对乙醇-蒸汽体系在二维竖直平板上的传质过程进行了模拟研究,发现液相传质系数随液相载荷的变化趋势符合渗透理论[33]。Haroun Y等也得到了两者正相关的结论[27]。 但Zhu M等认为传质效率随着液相流速的增大而降低,这是因为随着液相流速的增大,必然会导致液膜厚度增大,液相传质阻力增大,传质效率降低[34]。此外,Sebastia-Saez D等在三维倾斜60°平板上的物理性传质模拟研究发现,液相载荷与传质系数之间并不是单一的变化规律[35]。 随着液体流量的增加,会有一个最高值,这时由液相流量小导致的液体分布不均的状况有所缓解,同时接触时间较长,传质系数较大,之后随着液体流量的增加,液体速度变快,相间接触时间变少,相间传质系数变小。
此外,Sebastia-Saez D等认为液相流量在液体发展的不同阶段起着不同的作用,当传质由对流传质主导时,符合渗透理论,液体流量越大则接触时间越少,传质速率越大;而当液体发展到稳定状态时,传质由扩散传质主导,此时结论相反[20]。 Haroun Y等也认为液相载荷控制着传质模式,并将对流和扩散的分割点定为1/(4π)的两相接触时间[22]。
2.4 几何结构对传质的影响
除了改变物性参数和操作条件,也可以通过改变填料本身形状来加强传质,主要包括在填料板上添加小波纹、开孔及改变波纹倾角等。
虽然波纹板可以增强传质,但其增强传质的机理仍未得到充分研究。 李超对二维垂直平板与波纹板上的传质现象进行了模拟研究,发现在湍流状态下,波纹板会增加相界面间的湍动从而增强传质[36]。 Haroun Y等认为对传质有影响的是两相接触时间下的交界面形态,当液相雷诺数在一定范围内时,在波纹板的波谷区会出现旋涡从而影响两相界面,导致接触时间减少,传质增强;而随着液体厚度不断增大, 液体填满整个波谷后,漩涡区的增大不再影响传质[27]。Dietze G F模拟了层流状态(Re=15)下不同波纹结构上的气液两相逆流传质,研究结果表明波纹可以影响边界层的分布,进而影响相界面的位置,甚至造成浓度的重分布,即使是在层流状态下,波纹也能增强传质[37]。
Yu D等对普通填料波纹倾角进行修改,得到波纹倾角按照30°-35°-30°规律变化的独特折线式新型填料WPA,经过模拟和实验验证,变化的波纹倾角能够促进填料表面的液膜不断更新,有效提高传质效率[38]。
此外,Hu J等对开孔竖直平板上层流状态下的传质现象进行了模拟研究,结果表明表面开孔可以增加流动的不稳定性、改变薄膜流体的流动结构,从而增强传质[25,34]。 开孔会产生两个影响:一是当流体流过开孔区域时,速度在开孔处会突然增加,到达峰值,同时速度的增大会导致流体厚度的减少,从而减小液相传质阻力,导致此处增强因子增大; 二是流体会在开孔两侧来回穿流,开孔处的流动模式随着时间而变化,这种流动模式的波动也增强了传质。 但需要注意的是,虽然开孔结构是现有规整填料的共同选择,但对开孔填料的三维传质研究还未出现,因而开孔对传质的增强机理还未得到揭示。
张燕来对加入隔板后的JKB-250Y金属孔板波纹填料进行模拟计算, 发现隔板可使整场传质分布更加均匀,而且消除了两股气体交叉流动,通道单位压降降低了20%~50%, 传质系数提高约20%[39]。 然而,有实验表明,加入整个隔板后,液体分布不均加剧,传质性能下降,喻茹在JKB-250Y金属孔板波纹填料中加入不同长度的隔板后,发现存在最佳隔板边长(14.7~16.8mm),使得单位压降下的传质系数最佳(1.2~2.7m/s·(kg/m3)0.5)[40]。
3 结束语
基于CFD的规整填料板传质现象研究主要涉及传质数值模型和传质性能研究。 其中,浓度方程的推导与实现为传质研究奠定了良好基础,保证了传质模拟研究的准确性与稳定性。 但是数值模型的完备不能解决所有问题,规整填料本身复杂的几何结构、传质涉及到的多种变量以及传质与流动之间的复杂关系仍然是规整填料板传质CFD研究的难题。今后,规整填料板上传质现象数值模拟研究的发展可着力于以下3点:
a. 传质与流动现象紧密相关,不能脱离流动问题分析传质现象,应探索可定量描述两者间关系的关键物理量。
b. 规整填料几何结构对传质效率具有非常重要的影响,一方面应深入了解现有的开孔和波纹结构对传质影响的机理;另一方面应积极探索新型规整填料结构。
c. 传质现象涉及的工况参数复杂多样,现阶段对部分变量的研究所得到的结论呈现多样性,一方面由于研究所选择的体系不同,传质机理存在差异; 另一方面各参数的变化区间也并非一致。 因此,需要对更多参数进行综合探究,系统总结各变量对传质的作用,为实际工况提供参考。

