立足核心素养 打造高效课程——“天体运动问题高效复习课程”中习题优化设计方案

河北 侯建敏

近年来中国航天事业飞速发展，天体运动问题也随之成为高考命题的热点。考查方向常以万有引力定律和牛顿运动定律相结合分析天体、人造卫星以及宇宙飞船的运动，估算天体的质量密度问题以及估算天体表面的重力加速度问题等，还可以与运动学、动力学以及能量问题相结合，反映了物理学与现代航天科技的密切联系，激发学生对物理知识的学习热情和爱国情怀，从而渗透对物理学科核心素养的“科学态度与责任素养”要素的考查。通常以选择题的形式考查。

下面以两个高频考查方向为例，谈天体运动问题在复习课程中习题优化的设计方案。

一、天体质量和密度的估算

天体质量和密度的计算可通过以下两种方法进行

(1)自力更生法：在静止模型中，如果已知天体表面的重力加速度g和天体半径R，则

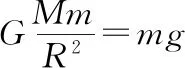
(2)借助外援法：在环绕模型中，如果已知卫星绕天体做匀速圆周运动的半径r和周期T

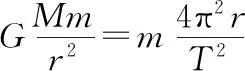
②若已知天体的半径R，则天体的密度为

以上两种方法中第一种方法是利用星球自身的物理量来估算星球自身的质量，所以称为自力更生法；第二种方法是利用环绕中心天体的运动参量来求中心天体的质量，所以称为借助外援法，注意此种方法只能求解中心天体的质量。

1.静止模型

【例1】2019年1月3日，“嫦娥四号”在月球背面软着陆成功，在实施软着陆过程中，“嫦娥四号”离月球表面4 m高时最后一次悬停，确认着陆点。若总质量为M的“嫦娥四号”在最后一次悬停时，反推力发动机对其提供的反推力为F，已知引力常量为G，月球半径为R，则月球的质量为

( )

【点评】本题是根据静止模型求解天体质量的问题，考查学生的理解能力和计算能力，是静止模型的直接应用，解题较容易。复习过程中在此知识层次上进行拓展，可以设计成两个物体质量或密度的比值问题，如下变式。

【变式1】热爱天文科学的某同学从网上得到一些关于月球和地球的信息，如下表所示。根据表格中数据，可以计算出地球和月球的密度之比为

( )

月球半径R0月球表面处的重力加速度g0地球和月球的半径之比RR0=4地球表面和月球表面的重力加速度之比gg0=6

A.3∶2 B.2∶3 C.4∶1 D.6∶1

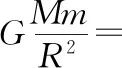
【点评】本题是根据静止模型求解天体密度的比值问题，难度较例1有所提高。在应用环绕模型求解天体质量时，可以不直接给出重力加速度，从而设计成先通过运动学或动力学以及功能思想求解出重力加速度，再根据静止模型求解天体质量，如下变式2。

【变式2】如图1所示，“健身弹跳球”是最近在少年儿童中特别流行的一项健身益智器材，少年儿童在玩弹跳球时(如图2所示)要双脚站在弹跳球的水平跳板上，用力向下压弹跳球，形变的弹跳球能和人一起跳离地面。该过程简化为：形变弹跳球向上恢复原状及人和弹跳球竖直上升。假设小孩质量为m，人和球一起以速度大小v0离开地面还能竖直上升h高度(上升过程小孩只受重力作用)，地球半径为R，引力常量为G，求地球的质量。

图1

图2

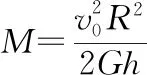
【点评】本题是根据静止模型求解天体质量的问题，先通过竖直上抛运动求解出重力加速度，再根据环绕模型求解天体质量，变式后难度较变式1又有所提高，知识框架增加了竖直上抛运动，实现试题多元化，利于搭建知识间的结合桥梁，充分考查学生的理解能力和分析综合能力。再进行深一层次的变式，可将圆周运动与万有引力相结合，求解星球表面重力加速度及星球密度，如下变式3。

【变式3】如图3所示，在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动，小球在最低点与最高点所受轻绳的拉力之差为ΔF，假设星球是均匀球体，其半径为R，已知万有引力常量为G，不计一切阻力。

图3

(1)求星球表面重力加速度；

(2)求该星球的密度。

设小球在最低点受到绳子拉力为F2，速率为v2，则有

小球从最高点到最低点的过程中应用动能定理可得

【点评】本题是根据静止模型求解天体密度的问题，先通过圆周运动的向心力公式和动能定理联立求解出重力加速度，再根据环绕模型求解天体质量，然后再求解天体密度，难度较变式2又有所提高，属于较难的问题。通过变式知识框架增加了圆周运动中向心力分析和动能定理的应用，使试题实现滚动复习，引导学生构建知识网络，使知识融会贯通，充分考查学生的理解能力和分析综合能力。

2.环绕模型

【例2】土星最大的卫星叫“泰坦”(如图4所示)，每16天绕土星一周，其公转轨道半径约为1.2×106km，已知引力常量G=6.67×10-11N·m2/kg2，则土星的质量约为

图4

( )

A.5×1017kg B.5×1026kg

C.7×1033kg D.4×1036kg

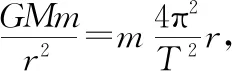
【点评】本题为根据环绕模型求解天体的质量的问题，考查学生的理解能力和计算能力，是环绕模型的直接应用，解题较容易。复习中可在此基础上进行变式，拓展知识深度。

【变式1】20世纪人类最伟大的创举之一是开拓了太空的全新领域。现有一艘远离星球在太空中直线飞行的宇宙飞船如图5所示，为了测量自身质量，启动推进器，测出飞船在短时间Δt内速度的改变为Δv，和飞船受到的推力F(其他星球对它的引力可忽略)。飞船在某次航行中，当它飞近一个孤立的星球时，飞船能以速度v，在离星球的较高轨道上绕星球做周期为T的匀速圆周运动，已知星球的半径为R，引力常量用G表示，则宇宙飞船和星球的质量分别是

图5

( )

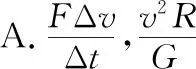
【点评】本题是根据环绕模型求解天体质量的问题，因为缺少轨道半径，不能直接套用公式，需要根据周期和线速度求出轨道半径，再根据环绕模型计算，难度较例2有所提高。通过变式本题的知识框架增加了圆周运动物理量的关系，选择此类试题或经某题进行变式，得到此类试题，可以使学生认识到圆周运动的天体中各运动参量之间是相互联系的，体现了用物理核心素养中物理观念要素来分析天体运动的能力。

【变式2】如图6所示，人造卫星P(可视为质点)绕地球做匀速圆周运动。在卫星运动轨道平面内，过卫星P作地球的两条切线，两条切线的夹角为θ，设卫星P绕地球运动的周期为T，线速度为v，引力常量为G。下列说法正确的是

图6

( )

A.θ越大，T越大

B.θ越小，v越大

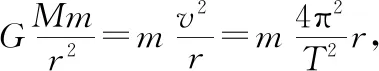
【点评】本题是根据环绕模型求解天体密度的问题。题目中卫星轨道半径未知，地球半径未知，需要根据几何关系准确地求出两量的比值，难度较大。通过变式，本题的知识框架增加了数学几何知识，试题通过此类变式可以充分考查学生的理解能力、应用数学解决物理问题能力和分析综合能力，体现对物理核心素养中科学思维要素的考查。

二、天体运动参量的比较和计算

由此可见天体运动参量a、v、ω、T均与卫星的质量无关，只由轨道半径和中心天体质量共同决定。

【例3】北斗卫星导航定位系统由地球静止轨道卫星(同步卫星)、中轨道卫星和倾斜同步卫星组成。地球静止轨道卫星和中轨道卫星都在圆轨道上运行，它们距地面的高度分别约为地球半径的6倍和3.4倍，下列说法中正确的是

( )

A.静止轨道卫星的周期约为中轨道卫星的2倍

B.静止轨道卫星的线速度大小约为中轨道卫星的2倍

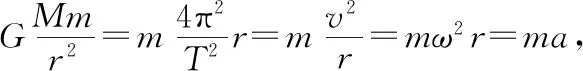
【点评】本题是根据环绕模型定量比较卫星运动的参量问题，考查学生的理解能力和计算能力，两卫星环绕的中心天体相同，所以比较卫星的运动参量只分析轨道半径即可，本题较容易，提高难度可以比较不同的中心天体和不同轨道半径环绕天体的运动参量问题，如下变式。

【变式1】科学家预测银河系中所有行星的数量大概在2～3万亿之间。目前在银河系发现一颗类地行星，半径是地球半径的两倍，质量是地球质量的三倍。卫星a、b分别绕地球、类地行星做匀速圆周运动，它们距中心天体表面的高度均等于地球的半径。则卫星a、b的

( )

【点评】本题为比较不同中心天体、不同轨道半径的环绕天体的运动参量问题，难度较例3有所提高，难度中等。通过变式虽然知识框架没有新增，但换成不同的中心天体后，可以加强学生对环绕模型的认识，考查学生的理解能力和建模能力，进行此类变式可使试题难度逐渐提高，便于学生接受。

【变式2】为照亮“嫦娥四号”驾临月球背面之路，一颗承载地月中转通信任务的中继卫星将在“嫦娥四号”发射前半年进入到地月拉格朗日点L2，如图7所示，在该点，地球、月球和中继卫星始终位于同一直线上，且中继卫星绕地球做圆周运动的周期与月球绕地球做圆周运动的周期相同，则

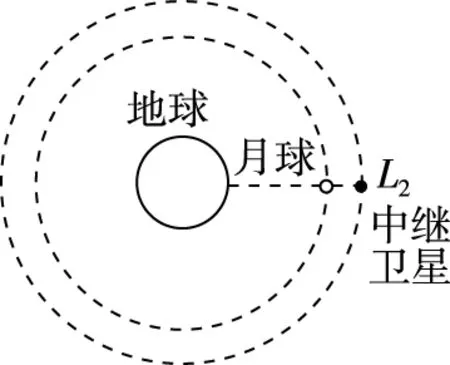
图7

( )

A.中继卫星绕地球做圆周运动的周期为一年

B.中继卫星做圆周运动的向心力仅由地球提供

C.中继卫星的线速度小于月球运动的线速度

D.中继卫星的向心加速度大于月球运动的向心加速度

【解析】中继卫星绕地球做圆周运动的周期与月球绕地球运动的周期相等，都约为27.3天，故A错误；中继卫星做圆周运动的向心力由月球和地球引力的合力提供，故B错误；中继卫星与月球同步绕地球运动，角速度相等，根据v=ωr，知中继卫星的线速度大于月球的线速度，故C错误；根据a=ω2r知，中继卫星的向心加速度大于月球的向心加速度，故D正确。

【点评】本题中继卫星的运动不是一个天体环绕另一个天体运动的环绕模型，而是中继卫星处于两个大天体的拉格朗日点上的运动，两个大天体对中继卫星的万有引力合力提供其做圆周运动的向心力。通过变式，本题的知识框架增加了天体在拉格朗日点的运动，这个模型与天体的环绕模型非常相似，如果不作受力分析，只是生搬硬套以往的环绕模型，本题的CD选项会错误地认为半径越大线速度和向心加速度越小。选择这类试题可以增强学生对环绕模型本质的理解，促进知识的迁移，所以本题最能考查学生的创新思维能力，体现了对物理核心素养的科学思维要素的考查。

本文系河北省教育科学研究“十三五”规划课题“课堂教学中培养学生核心素养的研究”(编号1604372)的研究成果。