“动态平衡问题”六大解题方法

福建 饶华东

“动态平衡问题”是考查“受力分析”“力的合成与分解”等相关知识的重要载体，可以考查学生的理解能力、推理能力、分析综合能力、应用数学处理物理问题的能力，历来是高考的重点和热点。下面从八个方面阐述“动态平衡问题”的解题方法，帮助广大考生全面突破该类题型。

一、精准作图，直观明了

【例1】(2016年全国卷Ⅱ第14题)质量为m的物体用轻绳AB悬挂于天花板上。用水平向左的力F缓慢拉动绳的中点O，如图1所示。用FT表示绳OA段拉力的大小，在O点向左移动的过程中

图1

( )

A.F逐渐变大，FT逐渐变大

B.F逐渐变大，FT逐渐变小

C.F逐渐变小，FT逐渐变大

D.F逐渐变小，FT逐渐变小

【解析】对O点受力分析如图2所示，由图可知在O点向左移动的过程中，F逐渐变大，FT逐渐变大，故选项A正确。

图2

【方法总结】作图法适用于三力平衡问题，且要求其中一个力大小和方向都不变(如题目中的重力mg)，另外两个力中至少有一个方向不变(如题目中的力F方向不变)。

二、相似三角，数形结合

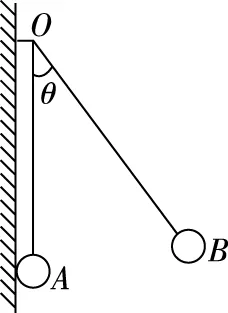
图3

( )

A.小球A受到细线的拉力大小不变

B.小球B受到细线的拉力变小

C.两球之间的库仑力大小不变

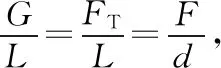
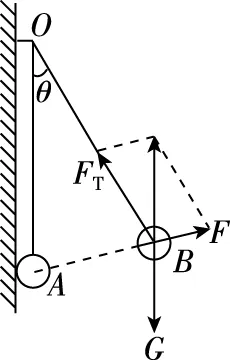
图4

【方法总结】当研究对象受绳(杆)或其他物体的约束，且物体受到三个力的作用，其中的一个力大小、方向均不变，另外两个力的方向都发生变化时，可以用力的矢量三角形与几何三角形相似的方法求解动态平衡问题。准确作图、仔细观察、灵活选用相似三角形的边角关系是解题的关键。

三、整体隔离，交替使用

【例3】如图5所示，粗糙水平地面上的斜面体将光滑圆球抵在光滑竖直的墙壁上，用水平向右的拉力F缓慢拉动斜面体，在圆球与地面接触之前，下列说法正确的是

图5

( )

A.水平拉力F逐渐减小

B.球对墙壁的压力逐渐减小

C.地面对斜面体的支持力大小不变

D.地面对斜面体的摩擦力逐渐增大

【解析】斜面体缓慢向右运动过程中，球缓慢下降，隔离球受力分析，受重力、斜面支持力和墙壁的弹力，根据作图法(图略)可知球受到的三个力大小和方向都不变，故B错误；把球和斜面当作整体受力分析，地面支持力等于整体的重力，大小方向不变，故C正确；地面对斜面体的摩擦力Ff=μ(m球+M斜面)g，大小方向不变，故D错误；对整体受力分析，水平方向上Ff=N墙+F，易知F为恒力，故A错误。

【方法总结】整体法与隔离法适用于多对象(两个对象以上)的动态平衡问题，一般用隔离法分析内力(对象间的作用力)变化，用整体法分析外力的变化情况，有时“先隔离后整体”，有时“先整体后隔离”，分析顺序要结合题意决定。

四、画圆辅助，巧解有方

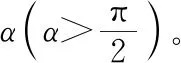
图6

( )

A.MN上的张力逐渐增大

B.MN上的张力先增大后减小

C.OM上的张力逐渐增大

D.OM上的张力先增大后减小

【解析】利用矢量圆辅助，如图7所示，重力保持不变，可用矢量圆的一条弦表示，FOM与FMN夹角保持不变，由图知FMN一直增大到最大，FOM先增大再减小，当OM与竖直夹角为β=α-90°时FOM最大，故AD正确，BC错误。

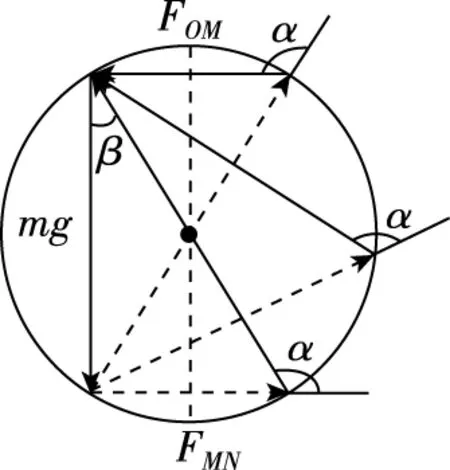
图7

【例5】如图8所示，在做“验证力的平行四边形定则”的实验时，用M、N两个测力计通过细线拉橡皮条的结点，使其到达O点，此时α+β=90°。然后保持M的读数不变，而使α角减小，为保持结点位置不变，

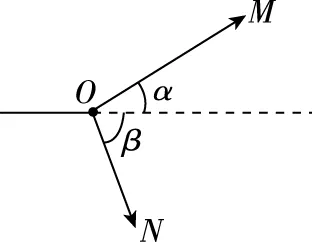
图8

可采用的办法是

( )

A.减小N的读数同时减小β角

B.减小N的读数同时增大β角

C.增大N的读数同时增大β角

D.增大N的读数同时减小β角

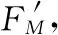
图9

【方法总结】作辅助矢量圆的方法常适用于两种情况：①物体受三个力作用处于平衡状态，其中一个力为恒力，另外两个力大小方向均变化，但夹角始终不变(如例4)，这种情况以不变的力为弦作圆，根据“同一段圆弧所对应圆周角为一定值”的数学结论，在辅助的矢量圆中作三个力的矢量三角形，从而可轻易判断各力的变化情况。②物体受三个力处于平衡状态，其中一个力为恒力，另外两个力中，有一个力大小不变，但方向变化，还有一个力大小和方向都变化(如例5)，这种情况以大小不变，方向变化的力为半径作一个矢量辅助圆，以指向圆心的力表示恒定不变的力，根据力的矢量三角形，容易判断出各力的变化情况。

五、正弦余弦，另辟蹊径

【例6】例4的另一种解法：

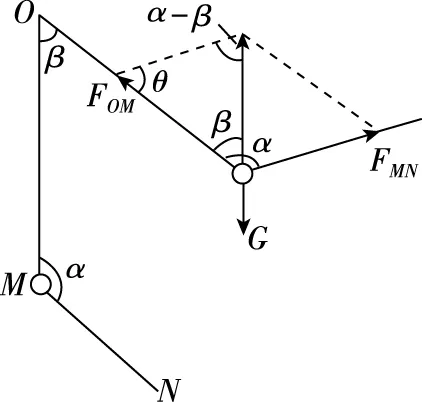
图10

【方法总结】三角函数、正(余)弦定理反映了三角形边与角之间的定量关系。物理量在合成或分解时会构成矢量三角形，若为直角三角形，可直接用三角函数或勾股定理分析计算，若为斜三角形，则通常要用到正(余)弦定理分析求解。

六、晾衣模型，几何约束

【例7】如图11所示，晾晒衣服的绳子轻且光滑，悬挂衣服的衣架的挂钩也是光滑的，轻绳两端分别固定在两根竖直杆上的A、B两点，衣服处于静止状态。如果保持绳子A端位置不变，将B端分别移动到不同的位置。下列判断正确的是

图11

( )

A.B端移到B1位置时，绳子张力不变

B.B端移到B2位置时，绳子张力变小

C.B端在杆上位置不动，将杆移动到虚线位置时，绳子张力变大

D.B端在杆上位置不动，将杆移动到虚线位置时，绳子张力变小

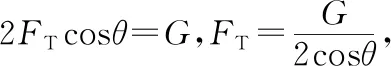
图12

【方法总结】对于“晾衣”模型，绳子拉力是否发生变化，关键看绳子总长及绳子左右两端点水平间距(左右晾衣杆间距)是否发生变化，只要绳子总长不变，绳子左右两端点水平间距不变，绳子拉力就不变，解题过程要充分利用绳子总长和绳子两端水平间距这两个几何要素对绳子拉力的约束，同时还要利用好力学对称性及几何对称性。

【试题预测1】某校气象研究小组用图13所示的简易装置测定水平风速。在水平地面上竖直固定一直杆，半径为R、质量为m的薄空心塑料球用细线悬于杆顶端O，当水平风吹来时，球在风力的作用下飘起来。已知风力大小正比于风速和球正对风的截面积，当风速v0=3 m/s时，测得球平衡时细线与竖直方向的夹角θ=30°。则

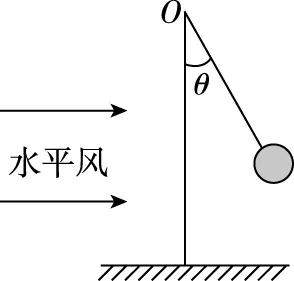
图13

( )

A.θ=60°时，风速v=6 m/s

B.若风速增大到某一值时，θ可能等于90°

C.若风速不变，换用半径相等、质量变大的球，则θ减小

D.若风速不变，换用半径变大、质量不变的球，则θ变大

【命题立意】本题以“简易风速仪”为背景，考查学生应用物理知识解决实际问题的能力，“物理思维”上考查学生的“模型建构能力”和“科学推理能力”，符合高考改革“增强应用性和探究性”的命题要求。

【解析】稳定状态下，如图14所示，塑料球受重力mg、绳子拉力FT、风力F处于平衡状态，当F=mgtanθ，θ=60°时的风力是θ=30°时的三倍，风速v=9 m/s，故A错误；稳定时，塑料球竖直合力为零，绳子不可能呈水平，故B错误；若风速不变，换用半径相等、质量变大的球，根据题意可知风力F不变，根据F=mgtanθ，质量m增大，θ应减小，故C正确；若风速不变，换用半径变大、质量不变的球，风力F增大，根据F=mgtanθ，质量m不变，θ应变大，故D正确。

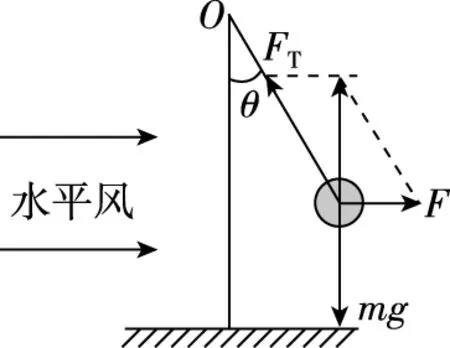
图14

【试题预测2】为迎接新年，小明同学给家里墙壁粉刷涂料，如图15所示，涂料滚由滚筒与撑竿组成。小明同学缓缓上推涂料滚，不计撑竿的重力以及滚筒与墙壁的摩擦力。撑竿对涂料滚筒的推力为F1，墙壁对涂料滚筒的支持力为F2，以下说法中正确的是

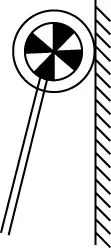
图15

( )

A.F1增大 B.F1先减小后增大

C.F2增大 D.F2减小

【命题立意】本题以“涂料滚”为背景，考查学生的“模型建构能力”，重在体现数形结合思想，符合本考点近5年高考考查方向，同时与高考改革中加强对“体、美、劳”的考查和应用的命题要求契合。

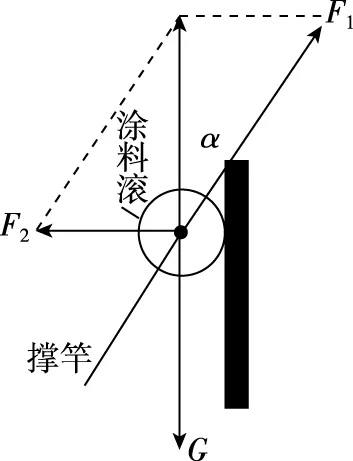
图16

本文系2019年福建省基础教育课程教学研究立项课题：基于物理学科核心素养培养的高中物理直观化教学策略研究(课题编号：MJYKT2019-197)研究成果。