步长自适应追踪法曲面求交技术的研究
刘 平 ,何雪明
1.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122
2.江南大学 机械工程学院,江苏 无锡 214122
1 引言
在人工智能、数控加工、实体造型和科学可视化等方面曲面求交技术应用十分广泛[1-2]。在基于逆向工程模型重建的过程中,高精度曲面求交是相邻曲面成功拼接的前提,参数曲面间常用的求交方法[3]有网格离散法[4-5]、分割法[6-7]、迭代法和追踪法[8]四种。其中网格离散法使用范围较广,通用性强,但求交过程中需要将整张曲面细密划分,若曲面较大,计算耗时增加明显;分割法是对网格离散法做出优化,将其求交过程中整张曲面的网格划分转变为仅对曲面间需要求交的部分进行划分,求交时间显著缩短。迭代法不能单使用,必须存在交点初值且该值必须尽可能的准确,初值选择不恰当会导致收敛不及时从而无法得到满足精度要求的交点,导致稳定性较差。追踪法是已知一个交点的确切位置,将其作为追踪起点,根据交线的几何性质,按照一定的步长继续搜索追踪下一个交点,不断重复这个的追踪过程,直到追踪到整条交线。相比其他方法进行曲面求交,追踪法[9]是一种人们普遍认为曲面求交的有效方法,追踪法的难点在于初始点获取困难、容易漏交、不好确定合理追踪步长。针对以上难点,国内外学者进行了大量研究。刘丽萍[10]采用包围盒测试的方法,在分割法的基础上得到了较为精确的初始点。史永丰[11]提出一种改进的基于微分方程的跟踪算法,选择边界点和拐点作为跟踪的起点,解决了漏交问题。涂海宁[12]采用抛物线逼近交线,求取抛物线满足条件的最大弦长,并以此弦长作为追踪步长求取交线,但此方法只适用于具有二阶连续的曲面,适用受到限制。为了保证求交精度,一般最简单的做法是取较小的固定步长值[9],但计算量会显著增加,导致计算速度变慢。
本文提出步长可自适应变化的优化追踪法,不同于传统的追踪法,该方法采用五次非均匀B样条曲线拟合交点,将步长与交线末端的曲率进行关联,得到可依据实际求交的曲面特征而实时变化追踪步长,适用范围广,求交稳定且速度快。
2 追踪法的基本原理
2.1 确定追踪起点
追踪起点选取是追踪法求交的第一步,求取初始交点首先需要将两个参数曲面转化成一组等参数曲线和一参数曲面[13],把参数曲面间的求交问题转化为容易求解的参数曲线与参数曲面求交的问题。计算跟踪起点,现以一组曲面为例,如图1所示。
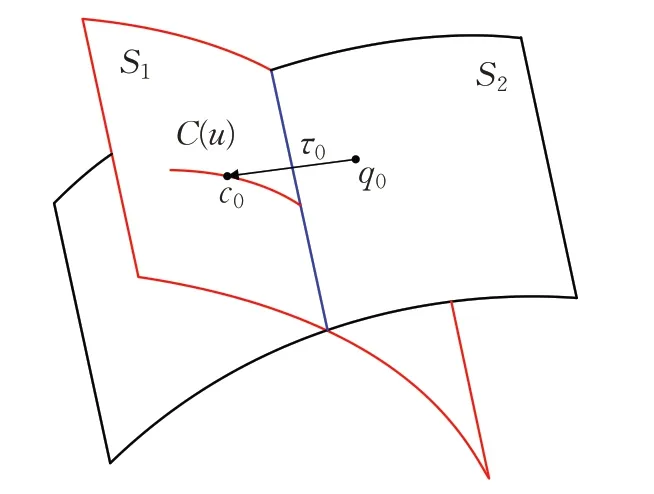
图1 确定追踪起点
在U、V方向上定义两个参数曲面,分别为S1=S1(u1,v1)与S2=S1(u2,v2)。把曲面S1上的一条U向等参数曲线定义为C(u),其方程可表示为C(u)=S1(u1,vˉ1),其中参数vˉ1表示该参数是固定值。c0=S1(u10,vˉ1)是曲面S1等参数线C(u)上的一点,同时q0=S2(u20,v20)是参数曲面S2上的一点。将c0与q0之间的矢量距离表示为τ0=c0-q0,倘若设定一个精度阈值ε,当 |τ0|≤ε时,即两个初始点之间的距离足够小时,则认为两曲面上的两个点c0与q0重合,即为两曲面的交点。
等参数线C(u)=S1(u1,vˉ1)的变量为u1,曲面S2对应的变量为u2和v2。求等参数线与曲面的交点,令:

对τ0=c0-q0用泰勒公式展开,忽略高次项可以得:

对上式进行赋范空间投影,在等式两边分别点乘S1u、S2u和S2v,则可以得到三个线性方程:
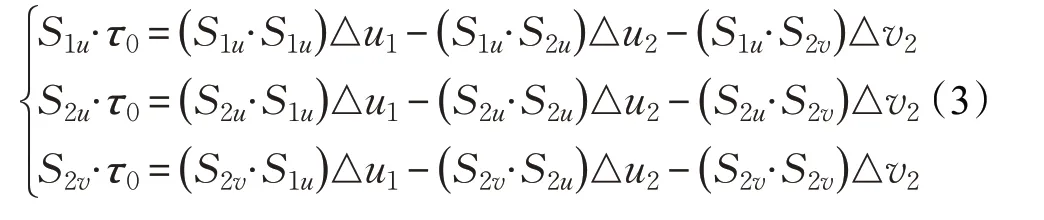
对方程组进行求解,可以求出△u1、△u2和△v2。此方程组由于系数矩阵正定,所以不会出现分母为0和不收敛的现象。将u10+△u1、u20+△u2和v20+△v2代入式(2)中,如此反复迭代计算,直到 |τ0|≤ε,则可以求得U向参数线C(u)与曲面S2的交点。通过对点c0采用泰勒公式展开,并依据赋范空间投影法进行迭代[14]。若C(u)和S2存在交点,c0将会在该交点处收敛。若C(u)和S2不存在交点,则点c0收敛于靠近S2距离最短的曲线C(u)上的一点,此时,寻找初始交点,应选取其余等参数线。
2.2 求取下一个交点
在求得初始交点后,接下来就要进行下一交点的求取,如此进行下去,就可以求得一系列交点,从而得到整条交线。进行下一个交点的求取,就必须知道该空间点的特征参数,需要对空间曲线上一点的几何结构进行分析。
2.2.1 空间曲线在一点的几何结构
了解空间曲线上一点的几何结构,有利于精确下一个交点的位置。假设空间曲线c=c(s)为2 阶参数连续曲线,c0=c(s0)是曲线c上的一点,s是弧长参数,则c0邻近点可由泰勒公式展开表示为:

在微分几何学中有:

其中,α、β和k为空间曲线c在点c0处的切矢、主法矢和曲率。依据切矢α和主法矢β可得到密切平面,记为Σ,进而得到空间曲线上点c0的几何结构[15],如图2所示。

图2 空间曲线上点的几何特征
将式(5)代入(4)的表达式中,舍掉高次项,可以求出c(s0+Δs)的近似值,记作c′(s0+△s):
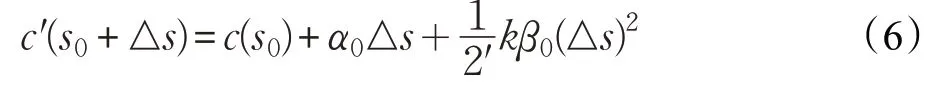
上面式子移项则等价于:

2.2.2 追踪下一个交点
在密切平面Σ上,将c0作为原点建立正交坐标系,α和β矢量方向作为互相垂直的坐标轴。在坐标系[c0,α0,β0] 中,把c0定义为起点,则有:弧长参数s0=0 ;步长△s=s,相邻点的坐标可表示为:

这样,就可以在密切平面上的正交坐标系内分析曲线上某一点处的结构特征。从式(8)看出,计算c′(s)的值,需要求出追踪步长s和等参数线上该点处的曲率k。
因为交线既在参数曲面S1中,也在参数曲面S2中,也因此可以借助两个参数曲面的几何特性间接获得交线的特征。c0选定后,便可计算出两个曲面在此点处的法矢,记为n1和n2,则相交线在点c0处的法平面就是法矢n1和n2组成的平面。相交线的切矢α垂直于法平面,可表示为:

因为交线主法矢β垂直于切矢方向,所以主法矢β一定处于由法矢n1和n2组成的法平面上。令曲率向量k=kβ=an1+bn2,取cos θ=n1·n2,两曲面的法曲率记为,曲率方程两边分别乘以向量n1和n2,则:
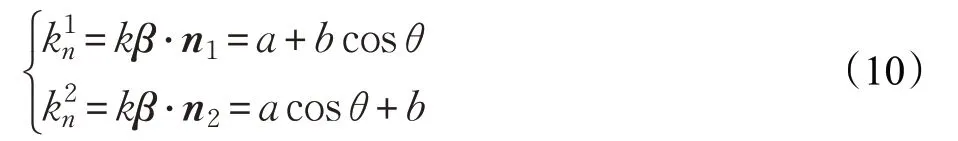
将a和b分别用表示,则:

所以:

根据曲面的第一基本形式可得:
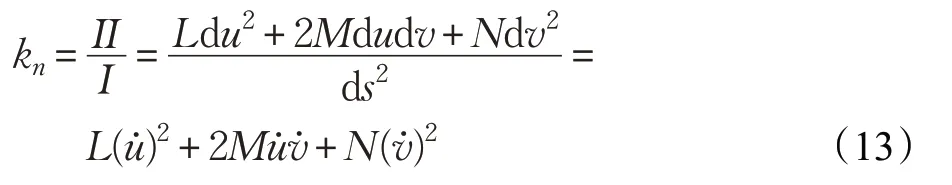

两边分别点乘Su和Sv,可以列出:

其中,E、F、G是曲面的第一类基本量。求解上式可以得到:

将式(16)代入式(13)中,可以求出曲面的法曲率。根据式(12),可以求出曲率向量k。根据曲率向量表达式可以求出主法矢β。曲线的曲率的大小为k的长度:
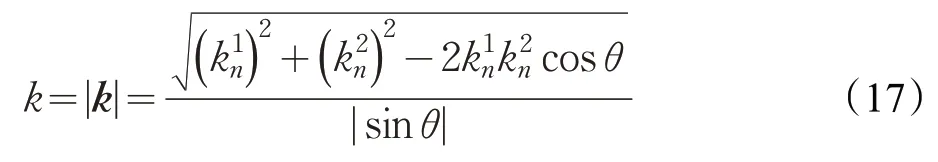
因此,可以分别求出曲率k、切矢α和主法矢β并和步长值s一起代入式(8)中,可求出下一个交点的近似位置。需要注意的是,想要得到该点的精确位置,还需要进一步迭代。
3 步长可自适应的追踪法求交
设定合理的步长值,可以得到较准确的交线位置和较高的求交效率。传统追踪法追踪步长都是固定值,步长大小根据经验均是人为设定,在针对复杂曲面求交时不够灵活方便,不够稳定。基于步长自适应的追踪法在求交过程中将追踪步长与交线末端的曲率半径相关联,使步长可根据曲面真实特征实时变化。
3.1 确定初始插值点
节点矢量的分布可以决定B 样条基函数的变化情况[16]。实验发现插值曲线的阶次为五次时,测量精度要高于三次和四次,而采用六次和七次曲线进行插值会产生振荡现象,反而测量精度降低。根据节点的变化规律[17],五次非均匀B 样条曲率具有连续性,其拟合的曲线平滑且符合常规产品的曲面特性[18],所以本文采用五次非均匀B样条曲线拟合交线上的点。
3.2 计算曲线末端曲率
若将五次非均匀B 样条曲线方程定义为C(u),则C(u)的末端点即为参数u=1 时所对应的点,曲线的曲率计算公式为:

其中,C′(u)、C′(u)分别为曲线的一阶、二阶导数。当kr <0 时拟合曲线沿前进方向顺时针弯曲;kr >0 时拟合曲线沿前进方向逆时针弯曲。曲线某点处的曲率半径可表示为:

3.3 确定自适应追踪步长s
值得注意的是:较小的追踪步长可以提高求交精度,但同时计算量增加;较大的追踪步长可以提高求交效率,但会影响求交精度,所以讨论合理的自适应追踪步长取值具有重要意义。
先按照固定步长求取六个交点,将六个点依次定义为Q0、Q1、Q2、Q3、Q4、Q5,然后采用五次非均匀B样条进行拟合。将固定追踪步长求取的六个交点插值为五次非均匀B 样条曲线后,如图3 所示,在曲线末端点Qp处以曲率半径r,构造该点处的曲率圆O1,连接O1Qp,给定一个跨距角θ,得到圆上的一点Qp+1,即为下一个追踪点,弦长QpQp+1即为跨距S,也就是自适应追踪步长值。确定自适应步长S的值后,也就确定了下一个追踪点Qp+1的大致位置。

图3 确定自适应步长原理图
AB为圆弧QpQp+1与弦QpQp+1的最大距离,当圆弧QpQp+1上的点到弦QpQp+1上的距离不超过阈值e,即AB<e时,可以用弦QpQp+1来近似表示圆弧QpQp+1,如下方程所示:


当θ=2×arccos(1-e×kr) 时 ,交 线 上 的 点 到 弦QpQp+1的距离为最大值e。根据上式可知,曲率kr越小,θ的值同时也会越小,AB值越大,自适应追踪步长的值就会越大;反之,当曲率kr越大时,θ值就越大,AB值越小,自适应追踪步长值就会越小。其中e的大小由测量精度要求决定,精度要求越高,e的值就越小,求交得到交点的数量就越多,一般取精度阈值e=0.01 mm。如图3所示,把自适应追踪步长S表示为:

确定曲率kr,即基本确定了自适应步长S的值。
3.4 基于自适应追踪步长曲面求交过程
需要注意的是根据自适应步长确定的下一个追踪点,得到的曲面交点位置并不精确,需要采用迭代法求出该交点的精确位置[19]。首先,分别在两参数曲面S1和S2上选取距点c′(s)较近的两个点,分别记为p1和p2,p1属于参数曲面S1,p2属于参数曲面S2。若有p1和p2收敛于邻近点c(s),则该点符合设定的精度要求:|p1-p2|≤ε。若p1和p2在邻近点处无法收敛,则将p2定义为交点的近似点,不断重复上述的计算过程。然后以迭代求取的精确点c(s)作为初始交点,继续计取下一个交点的位置,直至追踪到参数曲面的边界。追踪步长可自适应曲面求交过程的算法流程,如图4所示。
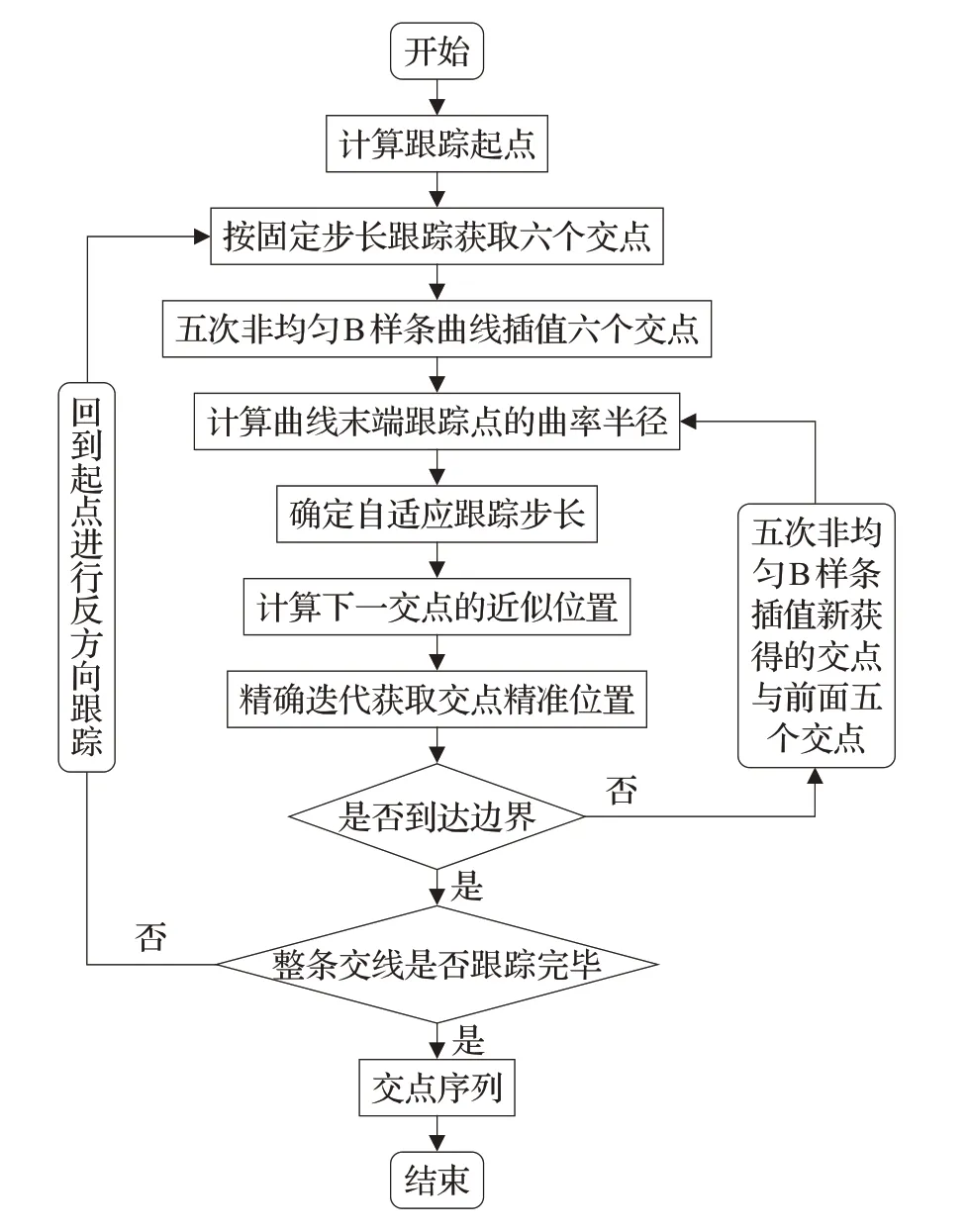
图4 追踪步长可自适应曲面求交过程
4 实例验证
为验证基于步长自适应追踪法求交相比传统追踪法求交的优越性性,提出对具有不同特征的曲面进行多组求交实验。将曲面在步长自适应和固定步长两种方式下进行求交,对比求交结果。需要说明的是:为方便求交结果的对比,以下所有求交试验均设置交点精度阈值ε为0.001 mm。
4.1 平面和自由曲面求交
为了验证五次非均匀B 样条曲线曲率连续自适应步长跟踪求交算法的可行性,结合C++面向对象开发语言和OpenGL 等图像数学函数,以平面与曲面、曲面与曲面求交为例,对曲面求交进行可视化。
如图5所示,为两个在逆向系统软件中重构出来的相交曲面,根据重构点云获取曲面边界信息,如图6 所示,曲面的U向跨距为12 mm,V向跨距为34.05 mm;平面的U向跨距为12 mm,V向跨距为32.1 mm。根据曲面边界信息,设置曲面U向、V向等参数线数量,如图7 所示,跟踪步长选择为自适应步长,精度阈值设为0.001 mm。求交结果如图8所示,蓝色的曲线即为平面与曲面的交线。

图5 平面与曲面相交模型
图7 跟踪步长设置

图8 平面与曲面求交结果
4.2 两个自由曲面间求交
平面与曲面求交实验验证了该求交方法的可行性,为了进一步验证该求交方法的通用性,选取更具代表性的自由曲面进行求交实验,如图9所示。与平面和自由曲面求交参数设置一样,先根据曲面边界信息设置等参数线数量,然后设置步长和精度阈值,这里依然选用的自适应步长,精度阈值设为0.001 mm,求交结果如图10 所示,结果验证了自由曲面与自由曲面求交的可行性。
通过平面与曲面求交、曲面与曲面求交实验验证了自适应求交算法的可行性后,为了进一步验证该求交算法的可靠性以及优越性,将自适应步长求交算法与固定步长求交算进行对比,并对其求交误差和求交速度进行分析。

图9 自由曲面相交模型

图10 自由曲面求交结果
实验分别以自适应步长、固定步长3 mm、5 mm、10 mm、15 mm 以及 20 mm 进行对如图9 所示的两自由曲面进行求交实验,求取不同步长下的交线,交线求取结果如图11 所示,从图中可以看出,当步长不断增大时,所求得的交线与实际交线偏移量越大,求交误差不断增加。

图11 不同步长求交结果
为了更好地反映误差与跟踪步长之间的变化关系,在imageware 软件中对误差进行了量化,分别绘制了自适应步长以及不同固定步长所求交线的误差云图,如图12所示。
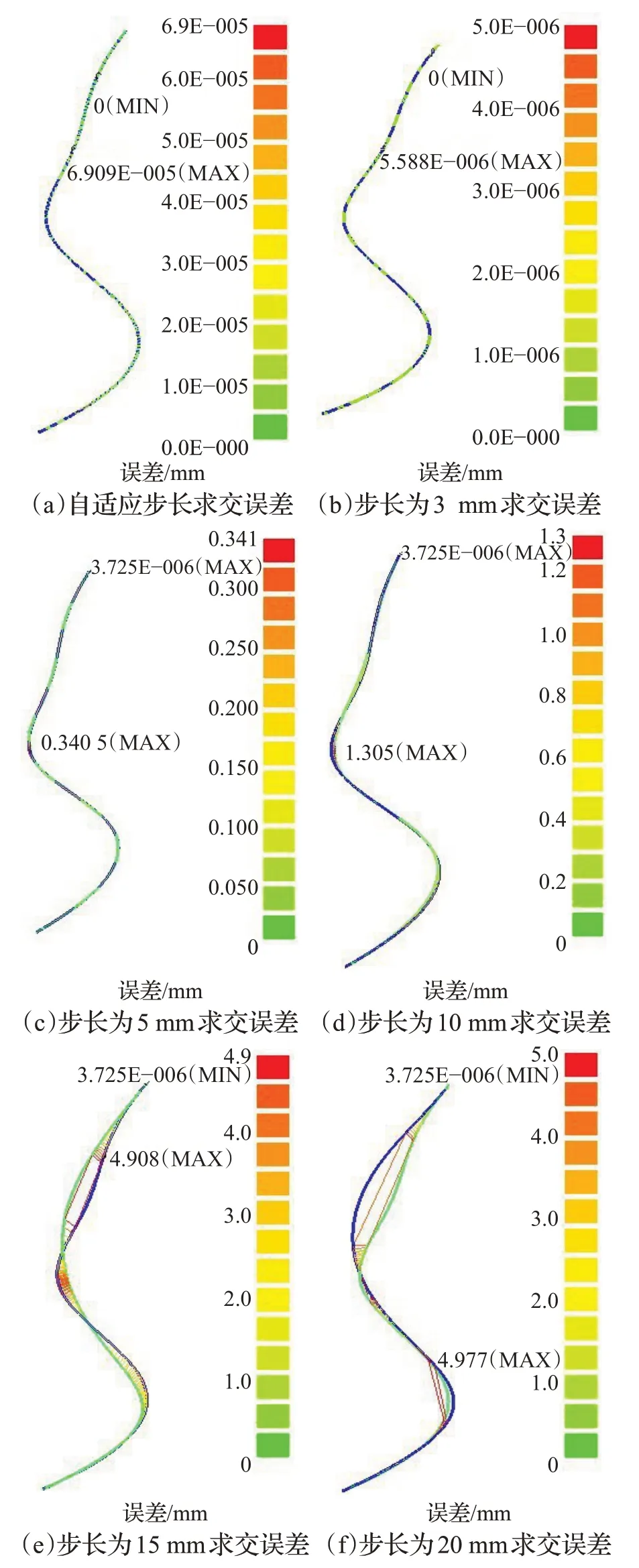
图12 不同步长曲面求交误差
图12 中蓝色线条表示所求交线,其他颜色线条用来反应所求交线与实际交线的偏离程度,其中最大偏离误差用MAX表示,最小偏离误差用MIN表示。可以看出,在曲线曲率较大的地方,误差明显增大。为了更直观地展现误差与跟踪步长之间的关系,量化误差。将误差进行数据统计得到表1。
从表1 可以看出,跟踪步长为3 mm 时交线的最大误差为5.588E-06 mm,最小误差为0 mm,平均误差为2.79E-06 mm,求交精度高;步长为5 mm 时,最大误差为0.340 5 mm,最小误差为3.725E-06 mm,平均误差为0.170 mm,求交精度一般;当步长为10、15、20 mm,平均误差为毫米级,求交误差较大,无法达到精度要求;采用自适应步长时,交线的最大误差为6.909E-05 mm,最小误差为0 mm,平均误差为3.45E-05,与步长为3 mm 时求交的精度接近,但是计算次数比步长为3 mm 时减少了43%左右,计算量减幅较大,计算量较小;与步长为5 mm时的求交相比,计算次数基本一致,计算量基本相同,但精度高出4个数量级。
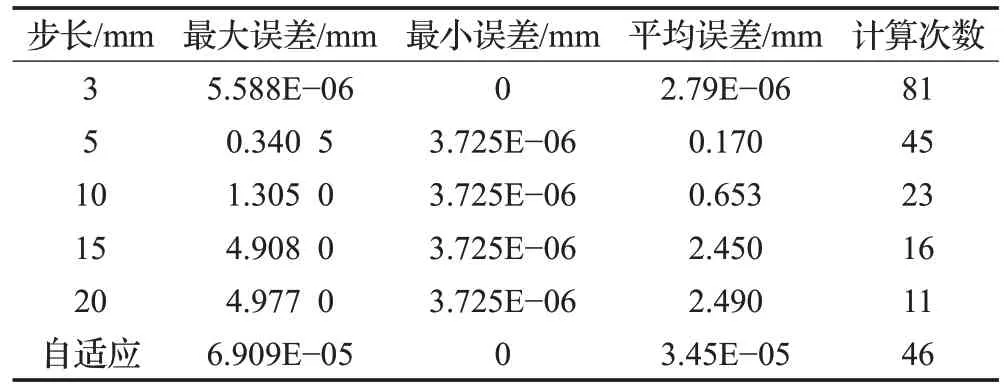
表1 多种步长下的交线误差
4.3 圆锥面与圆柱面间求交
找到含有规则曲面的实物,如图13所示,利用实验室已有设备CMM 对实物中标记的两个曲面进行点云采集。

图13 含有规则曲面的实物
将采集到的点云数据在SurfaceReverse 中显示,如图14所示。并进行曲面重构延伸相交,如图15所示。

图14 点云数据

图15 重构曲面延伸相交
设定精度阈值ε=0.001 mm,步长值取5 mm、14 mm及自适应步长,求交结果如图16所示。
为了更好地反映误差与追踪步长之间的变化关系,将自主研发的逆向系统SurfaceReverse 求取的交线与UG NX 求取的交线进行对比分析,将误差数据制作成表2。
从表2 可以看出,自适应追踪步长求得交点数为48,相比追踪步长为5 mm时计算次数减少了36.8%,但是两者误差相差不大,精度在同一个量级,均符合要求;步长为14 mm的曲面相交误差比较大,超过了误差许可范围。

图16 取不同步长值下的曲面求交结果

表2 不同追踪步长下的交线误差
通过对表1、表2的数据进行分析可以发现,对于传统追踪法求交,追踪步长越小,计算次数会显著增加,求取的交点数也会越多,计算量增多,求取交线的效率会降低很多,但求取的交线精度很高。相比之下,步长可自适应变化的追踪法求交,在满足同等求交精度的情况下,依旧可以保持较高的求交效率。结果表明:这种相交算法速度较快。
5 结论
(1)在求交过程中将追踪步长与交线末端的曲率半径相关联,得到可自适应变化的追踪步长。对具有不同特征的复杂曲面在步长自适应方式下进行求交试验,结果表明,在同一个误差许可范围内,相比传统的固定步长追踪方法,采用步长可自适应变化的追踪法进行曲面求交的交线平均误差均μm级,求交误差小,精度高。
(2)对同一组曲面在步长自适应和固定步长两种方式下进行求交试验,对比发现,固定步长过小,精度可明显提高,但计算量过大,耗时增加;固定步长过大,误差明显增加,得到结果不够精确。试验结果表明,基于步长自适应的追踪法求取到的交点不仅能随曲面特征合理分布而且具有更高求交效率。

