脑激活任务区分度的分析及应用研究

王工书，任尊晓，李丹丹，相 洁，王 彬

1.太原理工大学 信息与计算机学院，太原 030000

2.太原理工大学 大数据学院，太原 030000

1 引言

人类的大脑是身体中最复杂的器官。神经元是大脑中信号处理的基本单位，主要是通过电信号和化学信号进行活动。正是大脑中上亿的神经元共同协作工作才使人们拥有意识并且完成各种复杂的认知活动[1]。人们对大脑的活动和认知机制探索的需求促进了功能磁共振成像（fMRI）技术的迅速发展。fMRI技术的发展为脑科学的研究提供了很多的捷径，人们将fMRI 技术结合统计分析理论方法来探索大脑，研究大脑功能。任务态fMRI是在采集数据的同时要求被采集者执行一些实验范式，比如简单的记忆任务、识别任务等等。对大脑认知机制、记忆机制的研究以及各种精神疾病的研究有着重要的意义[2]。

任务态fMRI研究方向主要是脑功能激活分析。广义线性模型（Generalized Linear Model，GLM）是最常用的方法之一，它将被测血流动力学信号与受控实验变量关联起来[3]。在分析任务态fMRI数据时，使用广义线性模型对fMRI 数据中每个体素结合实验范式进行计算，来反映体素在任务条件下的激活强度[4]。以往的研究多分析大脑随着任务条件改变产生的激活强度的差异，进而分析大脑认知功能。这些研究利用任务态fMRI在神经影像学方面取得了重大的突破。但是这些方法都是在一些特定的任务条件下，选取一些功能重要、活跃性较强的脑区作为研究对象，并分析出大脑工作及其异常表相的脑机制。

近年来，越来越多的研究发现在特定任务下，大脑激活脑区中的体素呈现不同的激活强度。这些体素的激活反应大脑对任务激活模式，能更加准确地反映大脑认知状态。据此，Norman 等人选择特定区域内的体素的激活作为特征，使用SVM进行分类，判断被试正在看鞋子还是瓶子。结果表明用体素作为特征，可以很好地区分不同任务[5]。Kay等人设计了观察大自然图片的实验范式，在实验执行时进行fMRI数据采集，使用金字塔Gabor 小波模型（Gabor wavelet pyramid model）进行fMRI数据分类，依此判断被试观看什么图像，分类准确率在82%到92%之间[6]。相洁等人使用任务激活较强的区域的血氧水平变化值和时间序列作为特征对任务进行分类，并找出分类性能较好的体素[7]。Lange 等人提出应用广义学习矢量量化器对fMRI 数据进行分析，判断任务的类型，准确率在74%到76%之间[8]。Wang等人设计了观看房屋图片和人脸图片的实验范式，使用支持向量机进行分类，并研究了观看图片角度对分类准确率的影响[9]。这些研究通常选取一些功能重要、活跃性较强的脑区中的体素作为特征进行任务分类，以发现能表征任务状态的脑区及激活模式。这些基于分类算法的大脑激活的模式识别研究根据不同任务激活间的差异进行任务区分，具有较高的分类准确率，被应用于思维解码的研究中，通过大脑局部区域的激活来预测人类的思维。但是，因为分类模型与特征数据密切相关[10]，仅仅分类准确率不能很好地区分脑区激活模式对任务表征的好坏。特别是不同脑区具有不同的特征数量（体素），不能对准确率直接比较。

为了能更好地探索脑激活模式与任务间的关系，提出了任务区分度这一全新概念用于描述大脑中各个脑区对任务的表征性能，并提出一种脑激活任务区分度的计算方法，用于任务态fMRI 分析。大量的研究表明虽然大脑结构复杂，且大脑的各个脑区和神经元活动等方面与认知活动密切相关。但是在特定脑区中，相同和相似任务的大脑激活模式具有较高相似性，差别较大任务的脑激活则具有较低的相似性[11]。例如：物体视觉刺激任务在腹侧视觉皮层有广泛的激活，然而视觉运动刺激则在背侧视觉皮层有广泛的激活[1]。相似性度量是利用统计学方法分析两组特征的相似程度，例如相关系数分析，包括皮尔逊相关系数、斯皮尔曼相关系数和肯德尔相关系数等；距离分析，包括欧氏距离、马氏距离、切比雪夫距离和余弦相似度等。相似性度量可以直观地反应出两组特征间相近程度，并且具有较高的可信度。因此使用相似性度量的算法在体素水平上对不同的任务激活进行分析，可以表示任务间脑激活模式的相似度，反映脑区对任务表征性能，以揭示任务范式的脑机制。

该方法使用相同条件间的脑激活相似性与不同条件间的脑激活相似性之间的差异来表示大脑执行不同任务时激活模式的区分程度。差异较大表明该脑区对这些任务表征较好，差异较小表明该脑区对这些任务的表征较差。该计算方法为任务态fMRI的研究提供了新的研究思路，为大脑各个区域的功能和思维解码的研究提供了有力的帮助。本研究中的实验使用了皮尔逊相关分析、余弦相似度分析和欧几里德距离计算这3种相似性度量方法分析研究记忆提取任务的脑区激活模式，并进一步对狂躁症患者和正常人的任务区分度结果进行比较分析。最后将本文的结果与SVM算法的结果进行了比较。

2 数据采集与处理

2.1 数据采集

本实验的MRI 数据集来自UCLA 精神疾病学研究协会，并通过公共数据库OpenfMRI 获得。实验使用了45个狂躁症患者和55个身体健康正常人作为被试。

2.2 实验范式

情景记忆任务是一个经典的研究大脑记忆功能的实验范式。首先进行记忆编码，屏幕上每隔一段时间出现一个单词和一张图片的组合一共24组。记忆完成之后参与者躺在核磁共振仪中进行记忆提取，屏幕上间接性地出现72 组图片，其中24 组是图片记忆时出现过的组合正确图片，另外24 组是组合打乱的陌生图片。每组图片出现同时，屏幕下方有四个选项：“确定正确”“可能正确”“可能不正确”和“确定不正确”，让被试进行选择，依此来判断被试的记忆情况。剩下24 组图片的作用是“对照任务”，这些图片上只显示数字1、2、3或4，屏幕下方有1、2、3、4 这4 个选项，被试看到数字后选择对应的选项按钮。这3种图片在屏幕上随机顺序出现，在整个实验执行的期间对所有被试的大脑进行扫描，实验范式如图1（a）所示。本次研究中将采用记忆提取任务的数据进行分析和研究。

2.3 数据预处理

使用 Matlab 和 Statistical Parametric Mapping 12（SPM12）对原始fMRI进行预处理。预处理步骤包括时间校正、头动校正、去除线性漂移、去除白质和脑脊液等协变量、高斯平滑和滤波处理。预处理的目的是去除一些干扰因子，提高数据的准确性。

2.4 提取体素Beta值

fMRI数据预处理完成后，使用广义线性模型（GLM）对体素的时间序列进行处理。GLM模型使用典型的血流动力学反应函数（Hemodynamic Response Function，HRF）根据任务的起始时间对体素的每段时间序列计算，来预测每次任务诱发的大脑激活。每个体素将得到一系列Beta值，即体素每次任务下的激活水平。本实验中每个被试得到一个27 474（体素）×72（任务）的Beta矩阵。然后，基于Human Connectome Projec（tHCP）模版在把所有体素进一步划分为360个脑区[12]。

2.5 功能网络划分

根据Sadaghiani 等人的研究按照功能类型将所有脑区划分为14个功能网络，本实验对其中7个关键网络进行研究：视觉网络（VIS）、躯体运动网络（SMN）、锁骨网络（CON）、默认网络（DMN）、额顶网络（FPN）、听觉网络（AUD）、背侧注意网络（DAN）[13]。

3 脑激活任务区分度分析

3.1 任务区分度计算模型

相似性度量是指利用统计学方法评定两组向量之间相似程度。相同条件激活的相似度与不同条件激活之间的相似度的差值作为任务区分度。区分度越大表示大脑对不同任务的表征性能越好。脑激活相似度计算的模型示意图如图1（b）所示，具体方法如下：

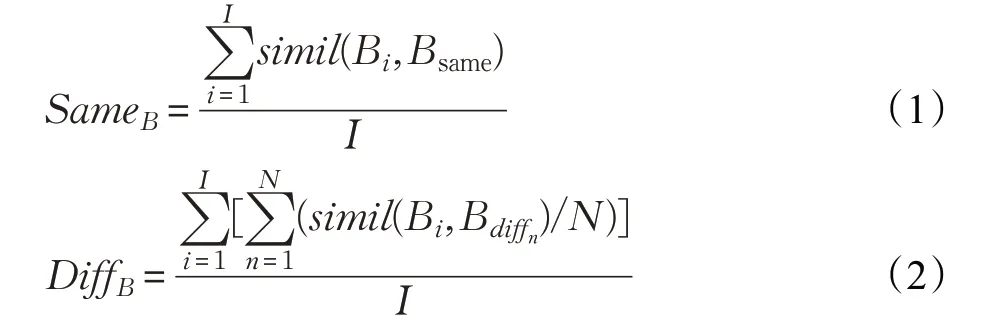
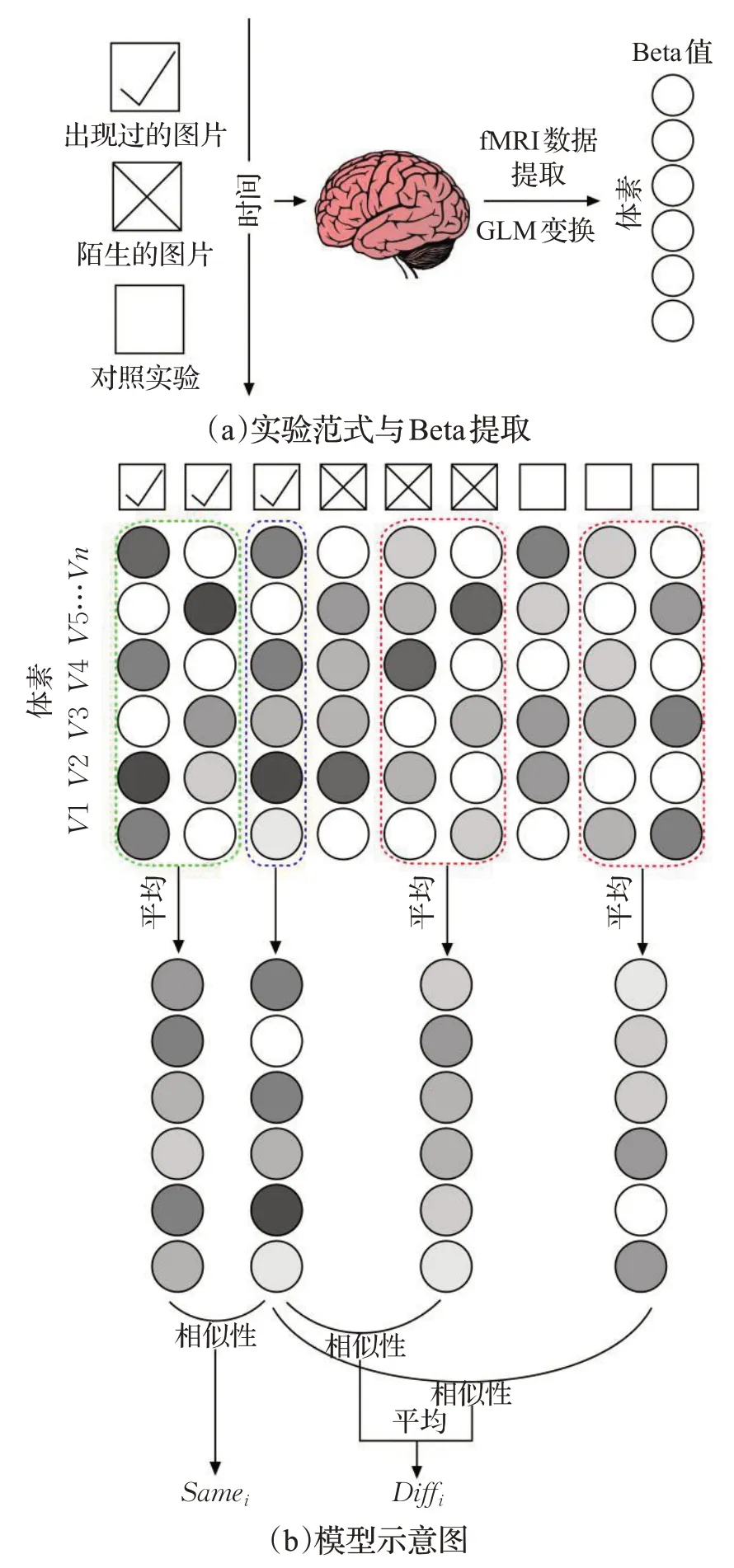
图1 实验流程

其中，I表示执行的任务总次数（在该实验中I为72），simil表示计算两个序列之间的相似度，Bi表示在实验中进行第i次任务时某脑区所有体素的任务激活，即Beta序列。Bsame表示与i任务的规则相一致的任务的平均Beta序列。Bdiffn表示不同任务规则的平均Beta序列（本实验中N=2，因为实验包括3 种规则，每个任务都对应2 种不同规则）。用TDB表示某区域任务区分度，公式如下：

之后将TDB进行单样本T 检验，TDB大于0，说明SameB和DiffB之间存在着差异。

3.2 相似性度量方法

本文提出的任务区分度是以相似性度量为基础。相似性度量的方法有很多种，每种方法都有各自的优势。为了找出适合脑激活区分度计算模型的相似性度量方法，采用3 种不同类型的相似性度量方法，包括皮尔逊相关分析、余弦相似度分析和欧几里德距离计算。皮尔逊相关系数计算公式如下：

其中，xi表示x变量中第i个值，xˉ表示x变量的平均值，yi表示y变量的第i个值，yˉ表示y变量的平均值，n表示变量的长度。其中x,y变量的长度必须相同。r的范围为-1 到1，负值表示负相关，正值表示正相关，r的值越大表示相关性越强。余弦相似度计算公式如下：

xi表示x变量中第i个值，yi表示y变量中的第i个值。余弦相似度是计算两个向量间夹角的余弦值，得到的余弦值越大说明相两个变量的相似度越高。欧几里德距离又称为欧氏距离，计算公式如下：

其中，xi表示x变量中第i个值，yi表示y变量中的第i个值。d越小说明两个变量间的空间距离越近相似度越高。如果使用欧氏距离作为相似性度量算法，SameBDiffB得到的大部分都是负值，为了便于3种方法间的比较，将使用欧氏距离算出的结果取相反数（即取-TDB为任务区分度）。

4 实验结果及分析

4.1 模型的准确性

利用本研究提出的基于脑激活区分度的任务态fMRI 计算模型，分析了正常人和狂躁症患者的大脑情景记忆任务的fMRI 数据，计算了各个脑区的任务区分度。选取阈值为p＜0.001（单样本T检验，Bonferroni矫正）来判断脑区对任务区分能力的显著性。脑区已经按照所属的功能网络标签进行分组排序（图2）。研究结果表明正常人和狂躁症患者在颞下回、尾状核、舌回、嗅皮质等区域存在显著的任务区分度，表明各个任务条件间的激活模式存在明显差异。这些脑区与大脑记忆提取状态存在显著的关联性[14-17]。图2（c）描述了正常人和狂躁症患者在角回、颞上回等区域存在显著差异（双样本T检验，p＜0.05），这些区域与疾病的病发密切相关[18-20]。为了更直观地表示结果便于分析，计算了图2中各个功能网络内显著脑区所占比例和网络的平均T值，分别如表1和图3所示。

图2 任务区分度计算结果

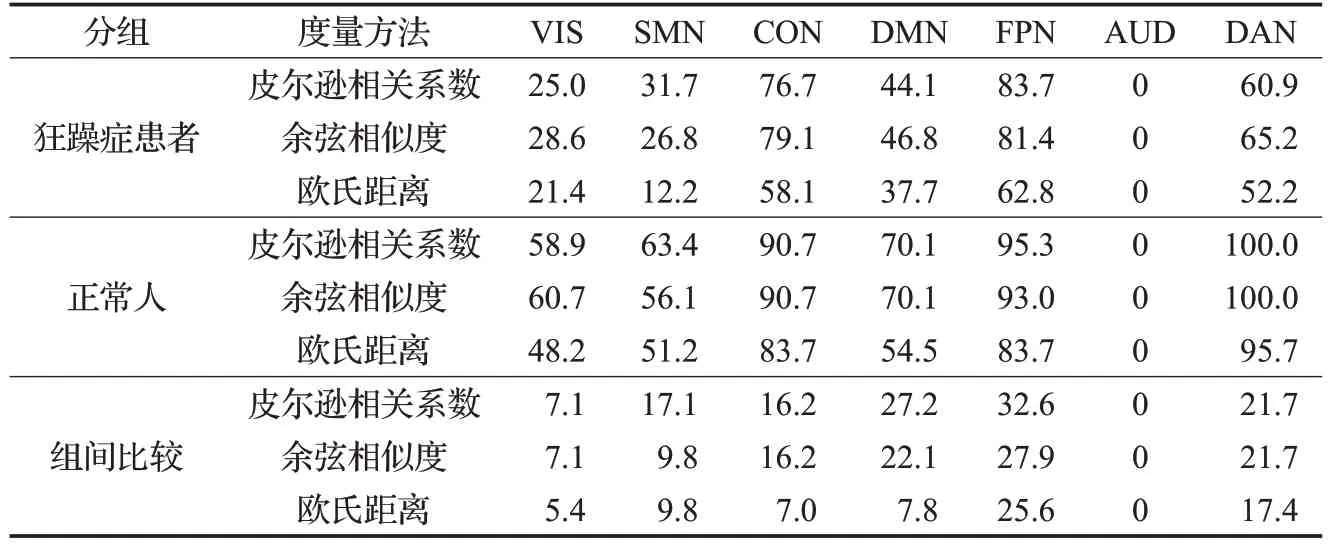
表1 子网络中显著区域比例 %

图3 网络的平均T 值

观察表1（狂躁症患者和正常人）和图3（a）、（b）发现FPN、DAN、CON 和DMN 这四个网络内的显著脑区百分比和平均T值要明显高于其余网络。该结果与之前大脑认知记忆科学的研究发现相一致。CON、FPN、DAN和DMN这4个网络与认知控制密切相关。CON、FPN和DAN在大脑进行记忆、信息处理、保持注意力等方面起着重要的作用，主导着大脑的思维活动[21-23]，在处理不同认知任务时激活模式有显著的不同，所以这3个网络的任务区分能力最强。DMN在大脑处于静息态或进行自我思考时活跃性较高，而与外界交互，进行认知、记忆等任务时活跃性较低[24]，本文的实验范式分为认知任务和对照任务（不进行认知活动，更多的是本能的反应），因此也表现出较强的任务区分能力。VIS 和SMN分别用来处理视觉信息和触觉信息但基本不参与认知任务，因此在实验中有较强的活跃性，但激活模式变化较少对认知任务的区分度相比其他网络较弱。整个实验都没有涉及到听觉任务，因此AUD 活跃性较低没有表现出任务区分能力。总之，任务区分度可以精确地表示出各个脑区对任务表征能力，可广泛应用于各种任务态脑功能分析。

从表1中的组间比较和图3（c）的结果中看出FPN、DMN 和CON 这3 个网络的显著脑区百分比和平均T要显著高于其他网络，表明在这3个网络中狂躁症患者与正常人相比任务的区分能力有显著的变化，这个结果与之前狂躁症的相关研究发现的结论相符。Dost 的研究表明，狂躁症患者DMN 中的一些区域的结构和正常人相比表现出异常的现象[25-26]。Baker发现，与正常人相比狂躁症患者在FPN 额顶叶控制网络中的功能连接性显著减少，发生中断显现；DAN中的功能拓扑结构发生很大的变化[27]。狂躁症患者的这3个网络所包括的脑区的结构和功能连接发生了改变，导致这些脑区在处理任务时产生异常的激活模式，从而影响到认知能力。上述的结果分析证明了任务区分度能应用于发现神经精神类疾病的脑功能异常。

4.2 相似性度量方法的比较

综合比较表1 和图3 中3 种相似性分析方法的结果。发现无论是各个网络显著区域百分比还是平均T值，欧氏距离计算的结果最差，余弦相似度分析的结果较好，皮尔逊相关分析的结果最好。欧氏距离可以直观地表示两个向量在空间上的距离，但是它将样本中不同属性之间的差异等同看待[28]，而大脑中的各部分的结构都存在着差异即使是同属于一个脑区，每个体素的激活范围都不相同，将它们之间的差异同等看待必然会对结果产生很大的影响[29-30]，所以欧氏距离算出的结果的准确性最低。余弦相似度对两个向量的长度归一化，主要通过向量的方向间的角度来衡量相似度[28]。它主要考虑了Beta 序列方向间的差异，而忽略了数值间的差异。因此在分析不同数据时只要角度相似，就会计算出相似的结果，这也是进行组间比较时余弦相似度准确性较低的原因。皮尔逊相关分析是在余弦相似度的基础上进行了修正[31]，如今在医学信号、电信号和生物信号等领域被广泛运用。它不仅考虑Beta 序列之间方向上的差异还考虑了每个数值上的差异，因此结果的准确性最高。通过实验的结果和多方面的分析得出这样的结论：使用皮尔逊相关分析对大脑任务激活进行分析可以科学、准确地表示出大脑各个脑区的任务区分度，而且可以发现不同类型人群脑区任务区分度间的差异，为一些精神类疾病的研究提供了新的思路。

4.3 任务区分度计算与SVM方法的比较

任务区分度计算本文提出的一种全新方法，之前还没有类似的研究。为了证明任务区分度算法在描述脑区对任务表征能力时的优越性，又使用任务态fMRI 研究中常用到的SVM 方法对实验数据进行了计算，作为对比。将各个脑区所包含体素的Beta值依次作为特征，使用SVM多分类模型对不同任务分类。虽然分类准确率与任务区分度结果无法做直接比较，但可以通过两种方法算出的结论评估方法的好坏。图4（a）、（b）和（c）分别表示基于3 种不同相似性度量方法计算出的各个脑区的任务区分度的分布（图2（a）和（b）中结果），图4（d）表示使用各个脑区作为特征的分类准确率的分布（将分类准确率小于33.4%的脑区视为0，因为小于33.4%说明准确率小于随机分类）。任务区分度的结果可以明显表示出狂躁症患者和正常人的差异，这与相关的研究一致，而分类准确率的结果中没有体现组间的差异。此外，认知控制网络（CON、FPN和DAN）的平均分类准确率（狂躁症患者：36.97%；正常人：38.74%）和DMN的平均分类准确率（狂躁症患者：35.57%；正常人：38.46%）基本没有差异，这与正常结论也不一致。这个结果证明了本文的方法在描述脑区对任务区分能力时要优于SVM 分类算法，对不同任务的激活模式的识别有较高的灵敏度。

图4 任务区分度算法与分类算法的比较

5 结论

本文提出一种基于脑激活任务区分度计算的fMRI分析方法。该方法以相似性度量作为基础，对不同条件下的脑激活进行分析，用来评估大脑中在处理不同任务条件时脑激活模式的差异程度，揭示各个脑区对任务的表征能力。使用该方法对狂躁症患者和正常人两组fMRI 数据进行分析，结果证明该算法模型可以反映出大脑中各个区域在执行不同任务时的灵活性以及与思维状态的关联程度，为fMRI的研究提供了新思路，为大脑思维解码的研究提供了有力的帮助。此外，从结果中发现了两组被试的任务区分度之间的差异，表明了该技术还可以用来揭示精神类疾病的脑功能异常，有助于精神类疾病的诊断与治疗。