引入必经点约束的路径规划算法研究

王 磊，孙力帆

1.河南科技大学 国际教育学院，河南 洛阳 471023

2.河南科技大学 信息工程学院，河南 洛阳 471023

1 引言

机器人技术的发展是高端科技发展的前沿，路径规划技术则是机器人研究的一个重要领域，是实现机器人自主定位与导航的关键技术之一。路径规划是寻找连接起点位置和终点位置序列点或曲线的策略，其主要任务是使机器人能够成功避开环境中的各种障碍，并沿着最低代价的路径到达终点。路径规划可分为基于先验完全信息的全局路径规划和基于传感器信息的局部路径规划，全局路径规划的常用方法主要有遗传算法[1]、快速随机搜索树算法（RRT）[2]和蜂群算法[3]等。局部路径规划常用算法主要包括：人工势场法[4]、模糊算法[5]、A*（A-Star）算法[6]等。其中A*算法适应环境能力强，应用十分广泛。它是Dijkstra算法与广度优先搜索（BFS）算法的组合，在启发函数的指引下搜索地图中的网格点，选取当前代价值最小的网格点作为路径的扩展，直至找到终点。A*算法对环境反应迅速，但实时性差，运行效率低。高庆吉等人[7]于2012年提出改进启发式函数，利用加权的方法增加其可靠性，同时在确定扩展结点时考察其8邻域是否可信。Františ等人[8]于2014年提出了一种基于改进A*算法的移动机器人路径规划方法，分别进行了 Basic Theta*、Phi+*、RSR[9]、JPS[10]方法的改进，通过实验发现JPS扩展结点最少、速度最快，而Theta*能实现路径结果最优。李冲等人[11]对单边矩形扩展A*算法进行了改进，将相邻结点的两条重合边界替换为一条共有边界，运行速度显著提高。综合分析各种算法，本文引入必经点约束对结点扩展方向进行指导，通过降低A*算法搜索过程的盲目性，减少冗余结点扩展数量，提高路径规划效率。

有关必经点最短路径问题，国内外学者积累了丰富的研究成果。袁红涛等[12]提出了一种计算K优路径算法，并对Dijkstra 算法的实现进行改进，大大提高了效率。徐庆征等[13]提出了一种求解无环必经点最短路径问题的遗传算法，以自然路径形式作为染色体，采用单点交叉和引入必经点的变异算子，通过使路径长度短且包含必经结点多的染色体被优先选择进入下一代，实现三类必经点的最短路径搜索。冯琳耀等[14]提出了一种几何代数算法，用于解决必经点最短路径问题，但该算法主要用于规划结点数最少的路径而非代价最小的路径，且只适用于无向图，无法用于有向图路径规划。黄书力等[15]提出了一种基于Dijkstra的必经点集最短路径规划算法，但该算法规划出的路径有环，且只适用于无向无权网络。文献[16]提出的启发式算法可用于解决经过必经点的最短路径问题，但结果存在误差。

本文利用A*算法生成起点到必经点、必经点到终点的最短路径段，再对路径段进行拼接，得到一条最短路径。最后，在100×100 网格地图中采用8 近邻搜索方案对传统A*算法与改进算法进行实验对比，结果表明，改进后的A*算法能有效降低冗余结点的访问量，提高路径规划效率。

2 A＊算法介绍

A*算法相当灵活，适应性强，是非常受欢迎的路径规划算法。A*定义如下：g(n)表示从起点Start 到达某一结点m的实际路径代价，h(n)是启发式函数，表示从结点m到达终点End 的估计代价，f(n)=g(n)+ h(n)是算法综合评估值。网格地图常用的启发式函数有曼哈顿距离，欧几里得距离和对角线距离。A*搜索就是不断比较移动过程中扩展结点的f(n)值，将每一次的最小f(n)值点存入列表作为备选结点。

A*算法存在两种极端情况：（1）当启发式函数为0时，f(n)=g(n)，则A*演变为Dijkstra 算法，规划路径最优但算法效率降低；（2）当启发式函数远远大于g(n)时，f(n)约等于h(n)，此时A*演变成BFS算法，则不一定得到最优路径。如果启发式函数值小于实际代价值，则A*能找到最优路径，但是扩展结点更多，运行效率更低。如果启发式函数值比实际代价值高，则A*扩展结点较少，运行更快，但路径规划结果不一定是最优。

在障碍物较多的地图中，通过启发函数h(n)计算得到的理论代价往往比实际代价小很多，从而导致A*需要在不同方向上扩展更多的冗余结点，使得A*算法运行效率大大降低。因而需要在路径规划过程中适当增加辅助条件对扩展方向进行约束和引导，从而减少冗余结点的数量，提高算法效率。

3 必经点路径规划

要在满足最短路径的前提下有效约束搜索过程，减少冗余结点的访问量，可寻找一个最短路径必经点，用于路径规划过程中的方向指导。显然，在某个障碍物的边缘区域存在最短路径必经点。如图1 所示，从起点S到终点G分别经过A、B、C、D、E五个点可形成五条不同的路径，显然S-A-G长度大于S-B-G，S-C-G和S-D-G两条路径都需要绕行B点或E点，长度必然大于S-B-G或S-E-G，因而可知B、E 两点至少有一点是最短路径的必经点。

图1 路径示例图

依据障碍物在网格地图中的分布特点，将其划分成不同的群体，即障碍物块，再按照各障碍物块与起点的相对位置关系，由近及远形成一个障碍物块层次体系。将“起点-终点”向量作为参照系，计算各障碍物块中每个网格点到参照系的距离，选取与参照系有交集的障碍物块两侧最大点作为登陆点，再连接相邻障碍物块之间的所有登陆点，形成以各层次登陆点为中间结点的所有模拟路径。选取代价最小的topk条模拟路径作为样本，计算样本中所有登陆点的综合评分，得分最高者为最短路径必经点。

3.1 建立障碍物块层次体系

A*算法在搜索路径时如遇到障碍物则自动避开，向其他方向继续搜索，不考虑障碍物的分布特点与层次关系，对结点扩展方向无有效控制，因而需要对网格地图进行预处理，将所有障碍物网格点关联起来，建立层次体系。首先遍历地图中每个网格点，找到所有的障碍物点，将每个障碍物点8邻域内出现的障碍物归入当前障碍物点所属集合中。循环执行，直到将所有障碍物点完成归类，从而得到所有障碍物集合即障碍物块。

具体步骤如下：

步骤1建立网格地图对应的二维数组Grid、存放待检测结点列表ListObstacles、当前层次障碍物列表ObstacleBlock和障碍物块层次体系列表ListObstacle-Block。

步骤2依照地图网格序列，将未检测到的第一个障碍物网格点存入列表ListObstacles中，并向数组Grid的对应位写入true。

步骤3检测列表ListObstacles，如ListObstacles为空，进入步骤4；否则，令Current=ListObstacle.first，删除ListObstacles第一个结点。检测Current的8邻近网格点，如检测到障碍物且该障碍物在数组Grid中的对应位是false，则加入列表ListObstacles中，并将数组Grid的对应位设置为true，同时将Current结点加入Obstacle-Block中，循环执行步骤3。

步骤4将ObstacleBlock插入列表ListObstacle-Block，如Grid所有值为true，则程序结束，否则进入步骤2。

通过以上步骤对网格地图进行预处理，形成一个系统可识别的障碍物块层次体系，如图2所示。

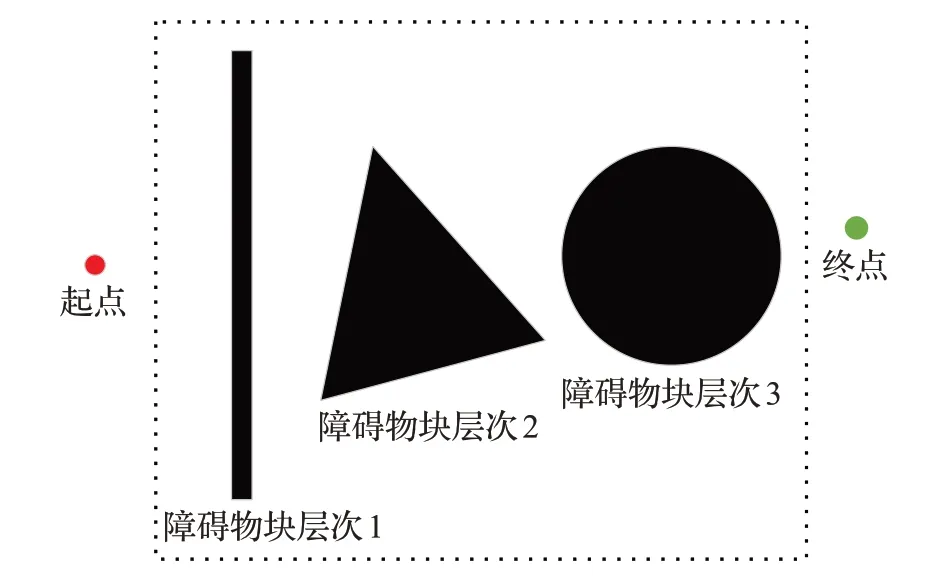
图2 障碍物块层次体系

3.2 计算登陆点

有障碍物遮挡的情况下，最短路径一定是沿着障碍物边缘扩展，如进入障碍物范围则无法通过，偏离障碍物又非最短路径，本文将最短路径可能经过的障碍物边缘点定义为“登陆点”。通过分析各种类型地图可以发现，登陆点大多位于障碍物块中距离“起点-终点”向量最远的障碍点附近，本文将“起点-终点”向量作为参照系，计算各层次障碍物块与“起点-终点”向量的相对位置关系，寻找障碍物块的边缘点，即登陆点。

使用T表示障碍物块层次体系，Bi表示第i个障碍物块，Gi,t表示第i个障碍物块中的第t个障碍物网格点，则有如下关系：

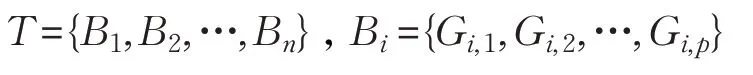
其中，n表示障碍物块的总数，p表示第i个障碍物块中所含障碍物网格点的个数。首先计算每个障碍物网格点与参照系“起点-终点”向量的相对位置关系，即障碍物点位于参照系的左侧还是右侧，障碍物块与参照系是否有交集。

利用“二维向量的叉积等于三个点组成的三角形‘面积’的两倍”这一特性来计算平面中某点与直线的位置关系，这里的“面积”值有正有负，可用于判断点在线段的左侧还是右侧。定义平面上的三个点分别为P1(x1,y1)、P2(x2,y2)、P3(x3,y3)，组成的三角形面积S(P1,P2,P3)=(x1-x3)×(y2-y3)-(y1-y3)×(x2-x3)。如果S(P1,P2,P3)＞0，则P3位于向量P1P2的左侧；如果S(P1,P2,P3)＜0，则P3位于向量P1P2的右侧；S(P1,P2,P3)=0，则P3位于向量P1P2上。

计算与参照系有交集的障碍物块Bi中每一个网格点Gi,t到直线“起点-终点”的距离，可利用点到直线的距离公式（1）来计算：

其中，A=yEnd-yStart，B=xStart-xEnd，C=xEnd×yStartxStart×yEnd，x0=xGi,t，y0=yGi,t。最后，分别选取障碍物块Bi位于参照系两侧的最远点作为登陆点。

3.3 最短路径必经点

登陆点位于各层障碍物块的边缘区域，包含了最短路径的必经点。使用D表示登陆点，则Di,l表示第i层的左侧登陆点，Di,r表示第i层的右侧登陆点。以图3蓝色实线所示，分别连接相邻层次的每个登陆点，可将障碍物块关联起来，形成大量的模拟路径：

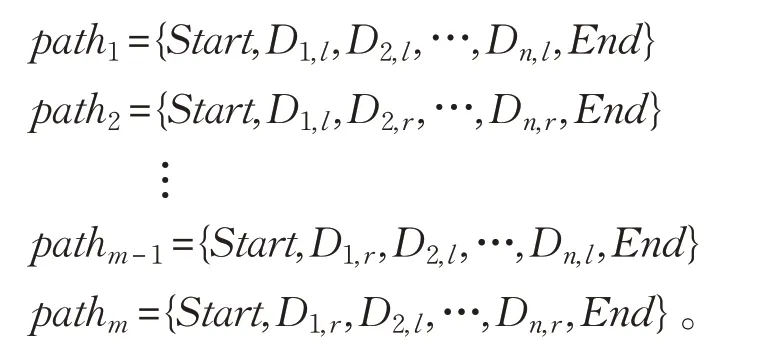
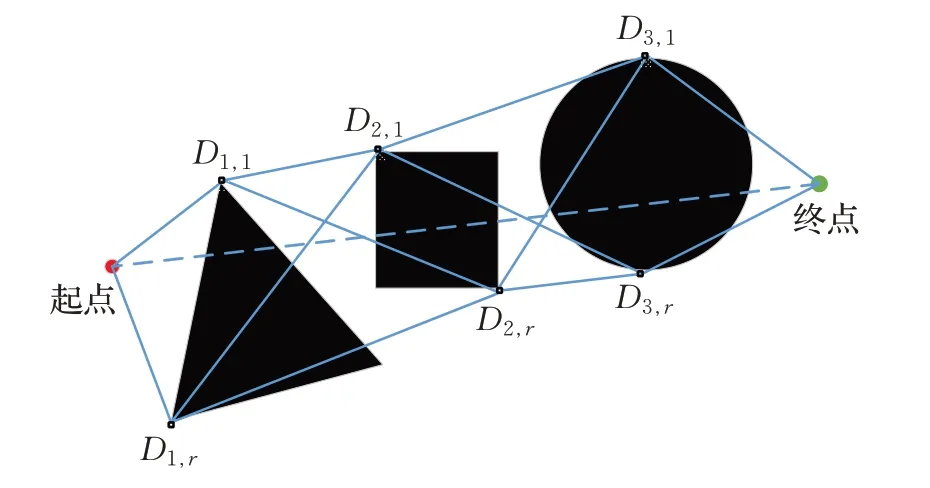
图3 登陆点连接图

然后，计算各相邻结点的欧式距离：

其中，(xDi,yDi) 和(xDi+1,yDi+1) 分别表示两相邻登陆点的平面坐标。计算每条模拟路径patht的路径代价选取代价最小的topk条模拟路径作为统计样本，再依据每个样本的路径代价在总体样本中的综合占比，计算每个样本的权重值：weight(u)=统计k条模拟路径中出现过的所有登陆点并计算其综合评分其中，pu(Dm,x)表示登陆点Dm,x在模拟路径pathu中出现的次数（0 或1）。选取F值最大的登陆点，即最短路径必经点。

最后，利用A*算法分别规划出起点到必经点、必经点到终点的最短路径段，通过拼接得到最短路径，并进行验证。

4 实验分析

在 Intel i7 四核处理器、8 GB 内存、500 GB 固态硬盘的计算机硬件平台上，使用C#语言编写A*算法与改进算法的Windows实验程序。

4.1 实验设计

将路径长度、算法运行时间和访问结点数量三个指标作为评价算法优劣的依据。在4幅100×100的网格地图中进行实验，分别运行传统A*算法与本文提出的改进算法，观察对比实验结果。

4.2 实验结果分析

图4 是A*算法与改进算法的路径规划效果图。图中左侧绿色网格点为起点，右侧红色网格点为终点，灰色网格表示障碍物，淡绿色网格表示算法访问过的结点，黄色线条表示规划路径。由图4 可见，改进算法的结点访问量明显少于原A*算法，具体实验数据如表1所示。在地图1中，改进算法比A*算法访问结点数量减少1 374 个，运行时间减少31.2 ms，效率提高66.7%；在地图2 中，访问结点数量减少1 711 个，运行时间减少39.3 ms，效率提高71.3%；在地图3 中，访问结点数量减少3 780 个，运行时间减少73.7 ms，效率提高82.5%；在地图4 中，访问结点数量减少3 277 个，运行时间减少46.9 ms，效率提高75%。

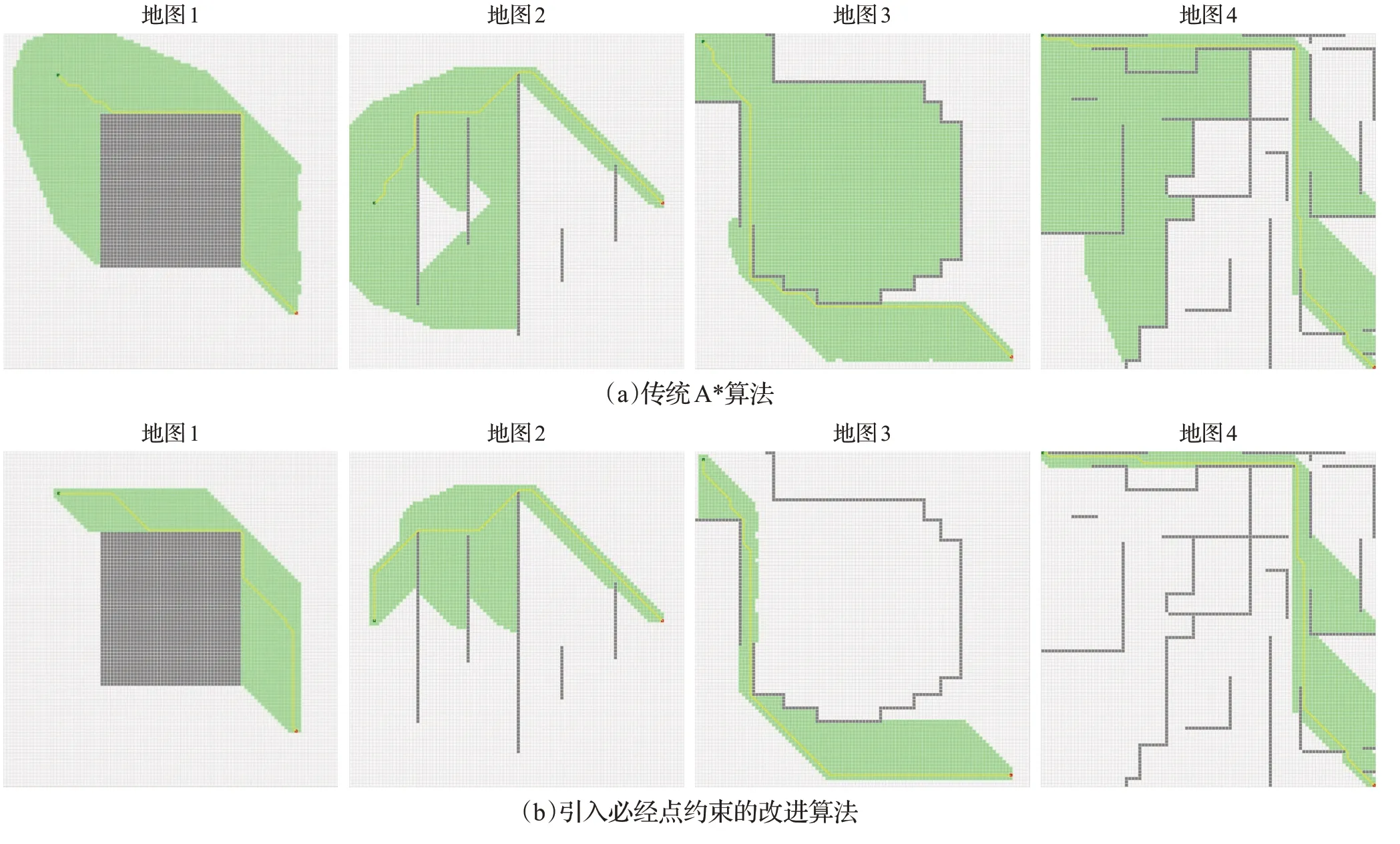
图4 两种算法路径规划效果图

表1 算法结果数据对比

实验结果表明，引入必经点约束的改进A*算法能够有效降低冗余结点的扩展数量，使路径规划效率大幅提高。

5 结束语

本文针对传统A*算法搜索范围广、运行效率低的问题进行研究，提出引入最短路径必经点的方法对搜索方向进行约束。首先将障碍物分成不同的层次体系，以“起点-终点”向量为参照系，计算出每层障碍物块的登陆点，再对相邻层次登陆点进行连接得到大量模拟路径，依据模拟路径的长度计算所有登陆点的综合评分，选取得分最高的登陆点作为最短路径必经点，利用A*算法分别对起点到必经点、必经点到终点进行路径规划，并将规划出的两条路径段拼接成一条最短路径。实验结果表明，改进算法可有效约束搜索方向，减少冗余结点的扩展，大幅提高路径规划效率。