自适应图学习诱导的子空间聚类

朱 丹，陈晓红，吴卿源，李舜酩

1.南京航空航天大学 理学院，南京 211106

2.南京航空航天大学 能源与动力学院，南京 211106

1 引言

在机器学习领域，子空间聚类受到广泛关注，可用于人脸聚类[1-2]、运动分割[3-4]等。子空间聚类方法是将特征选择技术和聚类技术相结合，在维度空间或数据空间中搜索可能存在的子空间，从而得到相应的子空间和聚类产生的簇[5]。具体而言，给定一组来自k个线性子空间{S1,S2,…,Sk} 的数据集X，X=[X1,X2,…,Xk]=[x1,x2,…,xn] ，其中Xi是子空间Si中样本构成的集合，子空间聚类的目标是将数据集X分成k个不同的簇，每一簇对应一个子空间。

迄今为止，人们提出了多种子空间聚类的方法，按照其原理大致可分为五种：矩阵分解法[6]、代数方法[7]、迭代方法[8]、统计方法[9-10]和基于谱聚类的方法[2-3]。本文基于谱聚类的方法进行研究。首先，利用给定的数据集X，构造关联矩阵Z，Z中的每个元素zij衡量了样本点xi和xj之间的相似性。数据集中的每一个样本点能用其他的样本点的线性组合表示出来，因此可以使用样本自表示来衡量两个样本点的相似性[11]，然后根据关联矩阵Z进行谱聚类。谱聚类是基于谱图理论的聚类算法，关联矩阵Z可以被看作图，数据聚类问题转变为图最优切割问题。由于块对角图能够更准确地描述数据聚类结果，因此通常期望关联矩阵Z具有块对角稀疏性。

以下几种算法都是基于谱聚类的方法，但是其关联矩阵有所不同。稀疏子空间聚类（Sparse Subspace Clustering，SSC）[3]通过对关联矩阵Z采用稀疏约束得到了稀疏的块对角阵。文献[12]指出如果一组样本点间的两两相关性很高，稀疏表示往往随机选择其中一对样本点。因此，SSC不能够很好地捕获同一子空间的数据结构关系，可能会将同一类簇的点分到不同类簇，得到错误的聚类结果。由此可见，SSC虽然获得了簇间的稀疏性，但是同时也会导致簇内稀疏，从而使得聚类结果并不理想。为了弥补SSC 的不足，Liu 等人[13]提出用低秩表示（Low Rank Representation，LRR）来代替稀疏表示。低秩表示在构造关联矩阵时加入了低秩约束，目的是考虑数据的全局结构，找到数据的低秩表示，根据这种表示可把来自同一子空间的样本点聚到一起。低秩约束可以有效降低噪声数据的影响，因此LRR对噪声和异常值具有较好的鲁棒性。文献[1]中的Example-1表明了当子空间正交时，LRR模型并不能保证得到一个块对角阵，因此低秩表示不能保证得到正确的聚类结果。为了得到块对角阵，Lu等人[1]提出了最小二乘回归（Least Square Regression，LSR），通过分组效应，即一组相关数据的系数近似相等，将高度相关的数据聚集到了一起。当子空间正交或者子空间独立、样本数据充足时，LSR 能够得到块对角矩阵，但是由于LSR 没有考虑数据间的局部相关性，导致块对角阵过于稠密。

以上方法均是在单视图数据上展开的，而文献[14]认为多视图学习比单视图学习方法有更好的泛化性，将单视图数据多视图化可提高学习效果。首先将单视图数据多视图化[15]，得到多视图数据。这些多视图数据的不同视图间的信息具有一致性和互补性[16]。而协同训练算法正是利用了不同视图数据的信息互补，提高了算法性能，受此启发，本文提出了一种自适应图学习诱导的子空间聚类算法（Subspace Clustering induced by Adaptive Graph Learning，SCAGL）。首先，通过多视图化的方法对原本的数据集进行特征分割，得到多视图数据集。然后，受到多视图谱聚类协同训练的启发[17]，将多视图数据子空间聚类与协同训练的思想相结合。通过建立引入图正则化项的最小二乘回归模型，对多个视图进行子空间聚类，基于协同训练的思想，使视图间的图信息可以互相利用，对多个视图的图正则化项进行优化，能够得到聚类性能更好的块对角关联矩阵。最后，对每个视图学习到的关联矩阵进行集成得到一个公共的关联矩阵，并以此进行谱聚类。本文的贡献在于：受协同训练的启发，有效地利用不同视图间的聚类信息，自适应地迭代更新每个视图的相似矩阵，从而得到更能反映聚类效果的块对角图，即块对角关联矩阵，它能更准确地描述数据聚类结果。虽然该方法是针对单视图数据提出的，它也可应用于多视图数据。

2 相关工作

2.1 最小二乘回归

假设样本数据充足且子空间独立，Lu 等人提出了基于最小二乘回归（LSR）的子空间聚类[1]。数据集X=[x1,x2,…,xn] ∈Rd×n，d是特征维数，n是样本个数，数据集中的每一个样本点能用其他的样本点的线性组合表示出来即X=XZ，为避免平凡解，规定diag(Z)=0 。Z∈Rn×n为自表示系数矩阵。LSR 的目标方程如下：

‖Z‖F是Z的F 范数，该范数约束使得自表示系数矩阵Z块对角化，去除Z中较小的系数[18]。

由于真实数据中通常包含噪声，为了减少噪声对聚类效果的影响，LSR 引入误差项E∈Rd×n，即X=XZ+E。LSR对误差项实行F范数约束，该方法可处理高斯噪声。文献[18]已证对误差项E实行L2,1范数可以探测异常值，得到如下的目标函数：

其中，λ为误差项的参数。当子空间正交或数据集充足，子空间独立时，F 范数约束使得Z具有好的块对角性，自表示系数矩阵Z能够表示样本间的相似性。但是，优化如上目标函数得到的Z是稠密的，为了提高Z的稀疏性，通常引入图正则化项。

2.2 引入图正则化项

LSR 在一定程度上提高了Z的块对角性质，但其只揭示了样本的全局信息，并没有考虑到数据点的局部内在相关信息，从而导致自表示系数矩阵Z过于稠密。已有的研究表明[19-21]引入图正则化项有利于保留数据的局部内在信息，对Z的非对角块部分进行稀疏约束，使得聚类效果更好。

首先由数据集X构造图G=(V,E)，V:={1,2,…,n}是顶点集，是边缘权重的集合，wij是顶点对(i,j)的边缘权重，权重矩阵W=(wij)n×n，本文主要使用k近邻来构造两个样本点间的权重。由于G是无向图，W=WT。度量矩阵D=diag(d1,d2,…,dn)，，图G的拉普拉斯矩阵L=D-W，从而得到目标函数：

其中，β是图正则化项参数。图正则化项tr(ZLZT)目的是希望同一类簇的样本之间的系数尽可能的一致。由于，目标方程也可写为：

2.3 多视图化的子空间聚类

文献[15]提出了将单视图数据多视图化的方法，即，对数据集X∈Rd×n进行分割率为α(0＜α ＜1) 的分割，得到s个新的子特征数据集，这s个子特征数据集可看做样本数据集的s个不同的视图。对这s个视图的数据，基于图正则化的最小二乘回归进行聚类，可得到s个对应的块对角系数矩阵，这可表示为：

如此得到各个视图对应的自表示系数矩阵Zi，由于每个视图的数据信息具有一致性和互补性，由式（5）得到的Zi包含着许多公共信息。文献[22]提出了最优自表示系数矩阵Z*，与Z*相比，每个视图的自表示系数矩阵Zi包含着各种噪声，Z*满足下式：

不难解得：

3 自适应图学习

3.1 协同训练算法

协同训练算法是由Blum A和Mitchell T提出的一种半监督学习算法[23]，协同训练算法适用于其特征可以自然分割为几个不相交特征集的数据集，在每个特征集上学习分类器，并通过结合这些分类器的预测结果，提高分类的正确率。文献[24]发现当特征集非常大且包含大量冗余特征时，把特征集划分为多视图数据集，协同训练算法可取得很好的效果。该文通过单视图数据多视图化，得到s个不同的视图X1,X2,…,Xs，利用标记样本训练出s个分类器h1,h2,…,hs，分类器hi从未标记样本中挑选若干个标记置信度高的样本进行标记，把这些由hi标记过的样本加入另外s-1 个分类器的训练集中，以便其他分类器利用这些新增的有标记的样本进行更新。这个过程不断迭代下去，直到s个分类器不再发生变化。

协同训练算法的成功实现需要满足三个前提：（1）每个视图能够单独地进行学习，即单视图能够学习出一个较好的分类器。（2）协同训练算法要求目标函数在每个视图上的学习结果相似度高。如果在某个视图内，分类器判断两个样本点属于同一类簇，那么在其他视图上也应该属于同一类簇，若两个样本属于不同类簇，其他视图上也应该属于不同类簇。（3）对于类别标记而言，不同视图是条件独立的。

3.2 基于协同训练优化图结构

受协同训练的启发，将其用于子空间聚类。每个视图上构造出的权重矩阵Wi包含该视图内样本之间的信息，每一列向量win表示第n个样本与其他样本间的相似度。根据相似矩阵Wi构造Laplacian图，由谱聚类算法[25]可知，图Laplacian 矩阵Li的前c个特征向量组成特征矩阵Ui，Ui中的每个列向量代表一个簇，对Ui进行k-means聚类。如果矩阵Ui的第n行分配给第k类簇，样本点xn就被聚到第k簇。因此Ui中的每个列向量是c个类簇的指示向量，包含了c个类簇的判别信息。受协同训练思想的启发，文献[17]提出用其他视图的聚类信息来迭代更新每个视图的相似矩阵，再对该视图的图结构进行优化。包含了各视图对聚类的判别性信息，将相似向量投影到这些特征向量的方向上，以保留聚类所需要的信息，并去除影响聚类结果的簇内信息。然后将其反投影到原始的向量空间中，获得优化后的图结构，即相似度矩阵进一步，在双视图情况下举例验证了优化后的相似矩阵显示同一类簇内样本间的相似度会逐步趋于一致，这有助于将不同类簇分开。文献[22]中提出了使用本视图的信息来迭代更新相似矩阵的方法，即得到了较好的聚类结果。这说明本视图的信息有利于提高聚类的效果，结合以上两种思想，本文提出同时把本视图和其他视图的信息融入聚类过程，迭代更新相似矩阵由于不同视图的近邻信息具有一致性，使用所有视图的类簇信息来更新相似矩阵，这种新的方法使视图间的信息相互传递，由此得到的相似矩阵包含更准确的聚类信息。

3.3 模型建立与算法流程

在式（5）基础上引入图结构优化，得到目标方程：

利用增广拉格朗日乘子法[26-27]对目标方程（8）进行求解，其增广拉格朗日方程为：

其中，μ ＞0 为惩罚系数，Yi为拉格朗日乘子，· 为矩阵的内积。分别对变量Zi,Li,Ei迭代优化求解。

（1）求解Zi

对数据集Xi构造权重矩阵Wi，并计算图Laplacian矩阵Li，由Li的前c个最小的特征值对应的特征向量组成特征矩阵Ui，进而得到基于协同训练算法优化后的相似度矩阵，对称化后得。

（3）求解Ei：

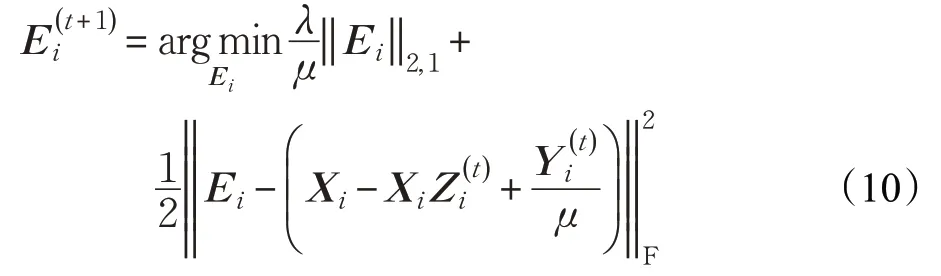
这可由收缩算子方法[28]求解。

本文提出自适应图学习诱导的子空间聚类算法（SCAGL），输入包含n个样本的数据集X与目标类簇数c，通过该算法可将n个样本聚到c个不同类簇，具体流程见如下算法。

算法1自适应图学习诱导的子空间聚类（SCAGL）

输入：数据集X，分割率α，误差项参数λ，图正则化参数β，聚类数c

输出：c个类簇

1.对X的特征维进行分割率为α的多视图化，得到s(s≥2 )个子特征数据集；

5.repeat

7.求得经过协同训练优化后的图Laplacian矩阵

9.更新各个视图的乘子矩阵Yi=Yi+μ(Xi-XiZi-Ei)；

10.更新参数μ=min(ρμ,μmax)；

11.until max‖Xi-XiZi-Ei‖＜ε或达到最大迭代次数

13.计算关联矩阵A=(Z*+Z*T)2；

14.对关联矩阵A进行谱聚类，将数据分割到c个类簇中。

4 实验结果与分析

4.1 数据集的选取

本文选取了4个不同数据集来进行实验，人脸图像数据集ORL、语音字母识别数据集Isolet、手写数字数据集 USPS 和 mfeat。在这些数据集中，ORL、Isolet 和USPS是单视图数据集，mfeat是多视图数据集。

ORL 数据集包含了40 个不同人的人脸图像，每个人在不同光照条件、拍摄场景和面部表情的情况下采集10张照片，将每张照片的大小修正为像素32×32。选取其中10 个人的照片生成一个100 个样本的数据集进行实验。

Isolet数据集是机器学习中用于聚类和分类的一种常用数据集。这个数据集的生成过程如下：150名试验者将字母表中的每个字母读两遍，每个受试者有52 个训练例子。数据集的特征维数是617，特征包括光谱系数、轮廓特征、声波特征等。选取前30个人的训练例子组成一个1 560个样本的数据集进行实验。

USPS 数据集是包含了数字0～9 的手写数据集，数据集的特征维数是256，每个数字包含了1 100 个样本。在 0～9 这 10 个数字中，手写时 3、5、8 三个数字容易混淆。因此，在本实验中选取3、5、8三个数字的样本进行实验。

mfeat 数据集是多视图手写数据集，是UCI 机器学习数据库的一个重要组成部分，其中包含了6个不同的视图 mfeat-fac、mfeat-fou、mfeat-kar、mfeat-mor、mfeatpix和mfeat-zer。每个视图的特征维数不等，包含2 000个样本，其样本已经有标签，即数字0～9，可用于对聚类算法分出的类簇进行评估。

4.2 聚类评价指标

4.2.1 归一化互信息（Normalized Mutual Information，NMI）

互信息用来衡量两个数据分布相关程度。设U和V是对n个样本集合X的两种不同聚类方法，记X={x1,x2,…,xn},U={U1,U2,…,UR},V={V1,V2,…,VC} ，首先定义互信息（MI）：

4.2.2 聚类准确率（Accuracy，ACC）

数据集X={x1,x2,…,xn} 包含了n个样本，聚类准确率指的是正确聚类的样本数占总样本的比例。U是实验得到的聚类结果，V为数据真实聚类结果，聚类准确率公式为：

4.3 基准算法

本文选取了6种经典的聚类算法进行对比。（1）k均值聚类算法（k-means clustering algorithm）[29]直接在数据集X上进行实验。（2）最小二乘回归（Least Square Regression，LSR）[1]目标是，解析解为低秩表示子空间聚类（Low Rank Representation，LRR）[2]的目标是表示系数矩阵Z的核范数。（4）稀疏子空间聚类（Sparse Subspace Clustering，SSC）[3]的目标是表示系数矩阵Z的1-范数。（5）块约束稀疏图下的子空间聚类（Block-wise Constrained Sparse Graph，SGB）[18]。（6）块约束下的集成子空间分割（Ensemble Subspace Segmentation Under Block-wise Constraints，ESSB）[22]。

与SSC、LRR、LSR、SGB 等算法相比，SCAGL 算法通过单视图数据多视图化将模型推广到多视图情形中，该算法不仅适用于单视图数据，也可应用于多视图数据。另外，与SGB、ESSB算法一样，SCAGL算法引入了图正则化项，利用了视图内的近邻信息。与ESSB算法相比，本文提出的算法使用所有视图的聚类信息来更新相似矩阵，使不同视图间的信息能够相互传递，由此得到的相似矩阵包含更准确的聚类信息。几种算法的对比参见表1。

表1 与基准算法的对比

4.4 实验结果与分析

4.4.1 单视图数据集上的实验

首先选取3 个单视图数据集ORL、Isolet 和USPS，为了计算聚类准确率和互信息，数据集的类簇标签是已知的。

选取6种经典聚类算法进行对比，自适应图学习诱导的子空间聚类（SCAGL）是本文提出的算法，其目标方程为式（8），该算法首先对数据进行多视图化，将单视图数据分割为多视图数据，由于分割方式不同，多视图化可分为顺序多视图化与随机多视图化。因此自适应图学习诱导的子空间聚类（SCAGL）可以根据分割方式分为 SCAGL-original 和 SCAGL-random 两种，SCAGL-original表示顺序多视图化后的聚类，SCAGL-random表示随机多视图化后的聚类。

对于这几种不同的算法，在每个数据集上单独执行30次实验，取其均值作为评价指标，如表2和表3所示。

表2 在单视图数据集上的聚类准确率（ACC）

表3 在单视图数据集上的归一化互信息（NMI）

由表2和表3可见，引入图正则化项后，算法的聚类性能普遍优于没有图正则化的算法。而与ESSB实验结果相比较，利用所有视图的聚类信息来迭代更新每个视图的相似矩阵比仅仅使用本视图的信息来更新相似矩阵得到的聚类结果要好。由此可见，不同视图间的图信息的共同利用至关重要。

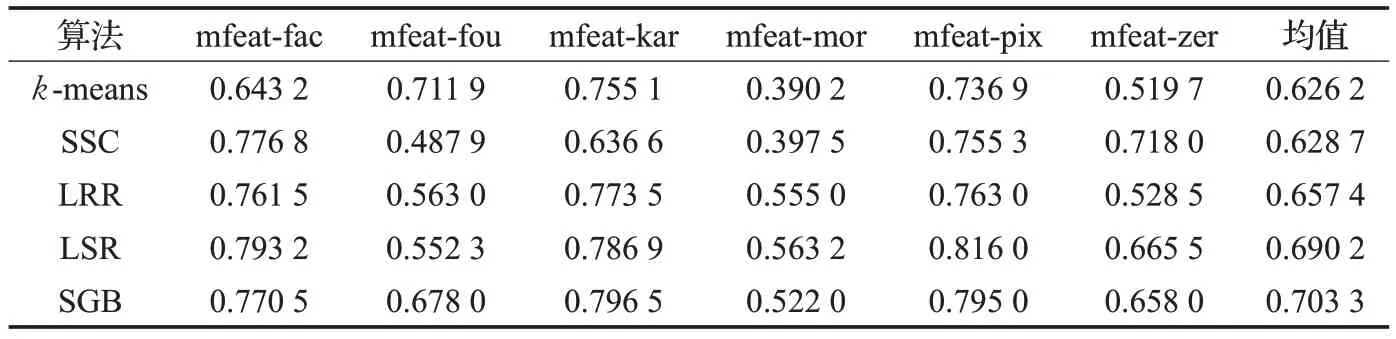
表4 在mfeat数据集上的聚类准确率（ACC）

表5 在mfeat数据集上的归一化互信息（NMI）

4.4.2 多视图数据集上的实验

在多视图数据集mfeat 上进行实验分析，该数据集包含了6个特征维数不等的视图。k-means、SSC、LRR、LSR和SGB这5个算法均是在单视图数据集上展开的，因此可以在该数据集的每个视图上单独进行实验，然后计算出每个算法在6个视图上得到的实验结果的均值，如表4和表5所示。

SCAGL、ESSB算法在单视图数据集上首先需要对数据进行多视图化，将单视图数据集分割为多视图数据集，而mfeat本来就是多视图数据集，因此可以直接在这两个算法上进行实验，得到的聚类准确率ACC 与归一化互信息NMI的结果如表6所示。

表6 在多视图数据集上的ACC和NMI

只能在单视图数据集上进行实验的算法SSC、LRR、LSR、SGB 和k-means 在 mfeat 数据集的每个视图上进行实验，然后取平均值作为聚类准确率与归一化互信息的值；ESSB、SCAGL直接进行实验，实验结果如图1。

由图1 可知，本文所提出的算法SCAGL 在多视图数据集上比起其他聚类算法具有较好的聚类性能。

4.5 参数对算法性能的影响

本节选取ORL 数据集来进行实验，研究算法中的不同参数以及视图分割方式对聚类结果产生的影响。选取一个要研究的变量，固定其他参数不变，每次进行30次实验，取平均值作为评判指标的值。本文研究的参数有分割率α、误差项参数λ、图正则化项参数β和算法迭代次数times。

4.5.1 分割率的影响

在本实验中采用顺序分割（Original）和随机分割（Random）两种分割方式，对分割率α分别取[0.5，0.25，0.2，0.1，0.05，0.025，0.02，0.01]来进行实验。目的是对比不同的分割方式与不同的分割率对算法性能的影响。该实验使用的其他参数一致，误差项参数λ=8、图正则化项参数β=0.02、算法迭代次数times=60。实验结果为图2。

由图2 可知，一般情况下，顺序分割的性能比随机分割的性能好。当分割率α=0.05 时，顺序分割方法的聚类效果达到最优；当分割率α=0.1 时，随机分割方法的聚类效果达到最优。当分割率小于某个临界值后，聚类准确率和互信息的值迅速下降，聚类效果越来越差，由此可见，并不是分割的视图越多越好。

图1 （a） 不同算法的准确率（ACC）

图1 （b） 不同算法的归一化互信息（NMI）

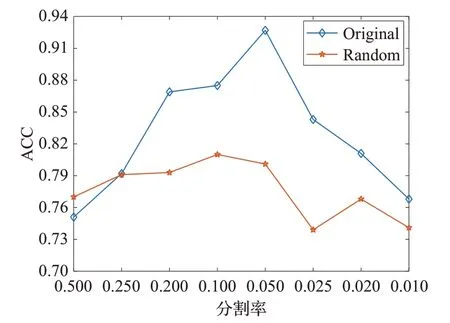
图2 （a） 不同分割率对算法性能ACC影响

图2 （b）不同分割率对算法性能NMI的影响

4.5.2 误差项与正则化项参数

在本实验中采取的分割方式为顺序分割，设置误差项参数λ以步长为2 在[2，22]的范围内变化，图正则化项参数β以步长为0.02在[0.02，0.1]的范围内变化。目的是研究误差项参数λ与正则化项参数β对算法性能的影响。实验中其他参数不变，设置分割率α=0.2、算法迭代次数times=50。

由图3可知，当误差项参数λ=12，图正则化项参数β=0.1 时算法的聚类性能最好，聚类准确率ACC 与归一化互信息NMI达到了最优，分别为0.905 3与0.877 6。

图3 （a） 误差项参数与正则化项参数对算法性能ACC影响

图3 （b） 误差项参数与正则化项参数对算法性能NMI影响

4.5.3 迭代次数的影响

本实验中采用两种分割方式顺序分割（Original）和随机分割（Random），对算法的迭代次数以步长10 在[20，120]的范围内变化。目的是研究迭代次数对算法性能影响。其他参数设置为分割率α=0.2、误差项参数λ=7、图正则化项参数β=0.01。

由图4可知当迭代次数达到50次时，算法性能比较好且趋于稳定，所以为了节约计算时间与计算成本，可以在实验中设置迭代次数在50次左右。

图4 （a） 迭代次数对算法性能ACC的影响

图4 （b） 迭代次数对算法性能NMI的影响

5 结束语

基于谱分析的子空间聚类首先由数据构造关联矩阵，再对关联矩阵进行谱聚类。因此，聚类的效果依赖关联矩阵的构造，本文提出了一种新的自适应图学习诱导的子空间聚类算法。首先将单视图数据多视图化，受多视图协同训练思想的启发，不同视图间的信息具有一致性和互补性，因此可以利用不同视图间的类簇信息，自适应地迭代更新每个视图的图正则化项，优化每个视图的图结构，得到聚类性能好的块对角关联矩阵，然后在关联矩阵上进行谱聚类，将样本聚到不同类簇中。进一步将本文算法与已有的聚类算法进行对比实验，实验结果显示了该方法的优越性。