智能无人机轨迹与任务卸载联合优化

张梦琳，江沸菠，董 莉，高 颖

1.湖南师范大学 智能计算与语言信息处理湖南省重点实验室，长沙 410081

2.湖南工商大学 新零售虚拟现实技术湖南省重点实验室，长沙 410205

1 引言

在万物互联的时代，越来越多的计算密集，延迟敏感和能耗高的新型应用不断涌现，例如自动驾驶、虚拟现实、体感网络等。由于用户设备（UE）的计算资源和电池容量有限，使得这些新兴应用无法在用户端有效执行[1]。移动边缘计算（MEC）被广泛认为是用于实现下一代物联网的关键技术[2]。MEC 是一种新型的移动计算方法，它打破传统云计算方式，不断提高用户服务质量（QoS）。与移动云计算相比，MEC减少了因数据中心网络堵塞而可能导致的延迟，通过将服务器部署到网络边缘（如接入点，小型基站等）使得云计算能力和IT 服务接近用户端[3]，这一技术不仅满足UE低延迟的要求，同时也降低了能耗，延长了设备的使用寿命。

在MEC 系统中，服务器的位置部署和计算卸载是实现能耗优化的关键点。由于服务器与UE是端到端的通信模式，所以它们之间相对较短的距离将消耗更少的传输时间和能量[4]。计算卸载包括数据传输、资源分配、MEC 执行计算和结果返回。虽然MEC 系统可以提供给UE 云计算的功能，但是也无法同时为所有UE 提供计算资源。所以，通过优化MEC 系统中服务器的位置部署和UE的计算卸载来平衡计算任务并提高系统能效至关重要。

目前，在MEC 系统中服务器的位置部署和任务卸载领域均已有较多专门的研究[5-12]，但很少有文献同时优化服务器位置和计算卸载来减少系统能耗。本文在无人机（UAV）上加载了3C 资源即缓存（Cache）、计算（Compute）和通信（Communication）资源，把无人机作为移动边缘服务器，为地面用户提供灵活的计算和通信服务，最大限度地减少服务时延，提高服务质量。基于以上分析，将MEC 服务器集成到UAV 上，并对UAV 的位置部署，计算卸载和资源分配进行联合优化。

考虑一种多用户-多无人机的移动边缘计算系统。通过重点优化UAV 的位置部署、计算卸载来减少能量消耗。特别是，UE 不仅需要决定是否卸载而且还需要确定卸载位置。本文提出了一种双层优化方法，上层利用h-SOM 神经网络根据信道增益作为判别依据对UE进行实时聚类得到UAV 的最佳位置，下层通过IDE 算法优化得到卸载矩阵。本文的主要贡献如下：

（1）研究了一种基于多用户-多无人机的移动边缘计算系统模型，依据此系统设计了一种具有时延约束的最小能耗计算问题，并针对该问题设计了一种双层优化方法对无人机轨迹和任务卸载决策进行联合优化。

（2）双层优化方法的上层采用无监督学习的h-SOM神经网络，对于网络的输入即每个UE 的坐标以信道增益作为判别指标，SOM网络能够自动找出UE之间的类似度，达到对UE 进行实时聚类的效果，从而得到UAV的最佳位置。

（3）双层优化方法的下层用一种改进的差分进化算法求解任务卸载决策和计算资源分配。首先将上层UE的聚类结果转化为一组可行解作为IDE 算法的初始解之一，然后利用带有精英初始策略和自适应双变异策略的差分进化算法对目标函数进行全局搜索，得到任务卸载决策和计算资源分配的全局次优解。

（4）针对本文所提方法，考虑了一个大规模场景，包含上百个UE 和多个UAV。研究了联合双层优化方法的可行性，并与传统算法进行了比较，验证了该方法的有效性。

2 相关工作

UAV的轨迹优化和计算任务卸载都是MEC系统中的研究热点。

在UAV的轨迹优化领域：Mozaffari等人[5]使用圆填充理论（Circle packing theory）设计将多个UAV有效的部署为无线基站，使UAV 的总覆盖面积和覆盖寿命最大化；Liu 等人[6]将块坐标下降法和连续凸逼近算法（Successive Convex Approximation）相结合提出一种新的SCA 算法来优化UAV 位置和无线回程容量的分配；Chen 等人[7]以误码率作为可靠指标，研究了基于最大可靠性的中继UAV 的最佳位置部署。Mozaffari等人[8]还研究了UAV的3D放置和移动性，以便最大化从地面接受物联网设备的数据等。

在计算卸载和资源分配领域：Wang等人[9]将深度学习技术和联合学习框架与移动边缘系统相结合，设计了“边缘AI框架”以优化移动边缘计算系统中的缓存和通信；Huang 等人[10]提出了一个基于深度强化学习的在线卸载DROO算法，该框架采用了深度强化学习来生成卸载决策；Chen 等人[11]研究了UAV 的最佳位置和UAV上缓存的内容，提出了一种基于概念的回声状态网络（Echo State Networks）的机器学习新算法；Wang等人[12]提出了带有移动云计算（MCC）的C-RAN 网络，研究了在给定任务时间约束下，MCC在C-RAN网络中的能量最小化和最优资源分配等。

与上述工作不同，研究了一个大规模场景下的联合优化方案，考虑到任务的时延约束和系统能耗，提出联合优化UAV的位置部署和计算任务卸载决策的双层优化方法。上述文献UAV的位置部署大多采用凸优化或分支界定法的方法来求解问题，虽然降低了问题的复杂性，但随着系统变量的增多，求解复杂度急剧增加，因此不适合大规模应用场景的问题。计算卸载用AI算法固然可以缩短时间，但算法中的神经网络需要大量样本，这在实际系统应用中难以获得。综合以上特点，本文考虑了一个多用户-多无人机的实际场景。针对该场景建立系统模型，并提出了一种双层优化方法，首先用一种无监督学习的h-SOM 神经网络对UE 进行实时聚类从而得到UAV 的最佳位置部署。该方法无需样本，并且可以在相对较短时间内得到UE的聚类结果。然后根据UE 的聚类结果，得到UAV 的最佳部署。最后采用IDE算法求解计算任务卸载决策。

3 系统模型

3.1 基于无人机的移动边缘计算系统

考虑由i∈I={1 ,2,…,I}个UE和j∈J={1,2,…,J}个UAV组成的MEC系统，如图1所示。UE随机分布在规定区域内。每个UE 有一个计算密集型任务要执行，该任务采用二进制卸载策略。和文献[13]相似，计算任务可以用数学模型描述为Ui=(Fi,Di,T),∀i∈I。其中Fi是完成任务Ui所需的CPU 周期总数，Di是任务Ui的卸载数据量，T是时间约束或用户的QoS要求。

图1 系统模型

计算卸载包含三个部分：（1）数据传输，（2）执行计算，（3）结果返回。本文参考文献[14]，只关心前两个部分，忽略结果返回。

3.2 通信模型

本节所述的通信模型体现在上行链路的传输。将aij={0 ,1},∀i∈I,∀j∈J表示UE的卸载决策。当aij=1时，表示第i个UE将计算卸载到第j个UAV上，当aij=0时，在本地执行计算。同时上述决策满足∀i=I，该公式意味着每个任务最多只能在一个UAV上执行。

假设UE 在数据传输中保持静止[15]。当UEi满足aij=1 时，第i个UE 卸载到第j个UAV 的传输速率rij可以用下式表示：

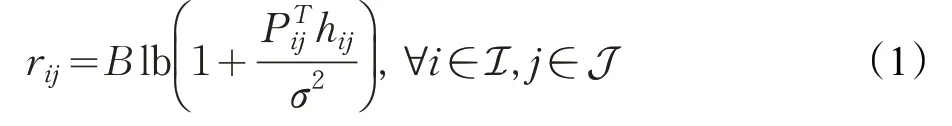
其中，B是信道带宽，是发射功率，hij是信道增益表示为是第j个 UAV 的高度，Rij是第i个UE和第j个UAV的水平距离，α是小尺度衰落分量。本文中设置UAV在相同的高度。

3.3 计算模型

本节介绍计算模型，主要描述计算任务在本地和UAV上执行的计算时间和能量消耗。

（1）本地执行。假设每个UE 在本地的计算能力为fiL，任务Ui所需的CPU 总周期表示为Fi，那么，第i个UE在本地计算所需时间为：

因此，第i个UE在本地执行所需要的功率PiE为：

式中，ki=10-27是有效开关电容，vi=3 是正常数[16]。

（2）UAV上执行。当UE决定将任务卸载到UAV上时，首先需要确定UE 是否在UAV 覆盖范围内，然后定义传输时间和UAV 上的计算时间，最后定义计算卸载所需能耗。根据下式判断第i个UE 是否符合第j个UAV的覆盖范围：

T为总时间。考虑到UAV 资源有限，所以fij必须满足以下约束这意味着每个UAV分配给UE的计算资源不能超过自身总计算资源。和文献[18]一样，忽略无人机悬停和计算所消耗的能量，第i个UE卸载到第j个UAV的能量消耗表示如下：

4 问题拟定与分析

4.1 问题拟定

基于以上系统模型分析，给出目标函数Q1如下：

式中，变量uav、a、f分别是UAV 位置矩阵、任务卸载矩阵和资源分配矩阵。约束条件的意义如下：C1 确保所有任务在UAV 或者本地执行；C2 表示如果任务选择卸载，则每个任务只能在一个UAV上卸载；C3是时延约束；C4 表示UAV 分配给UE 的资源不得超过自身总计算资源；C5表示UAV的覆盖范围约束。

4.2 问题分析

上述问题可以描述为一个混合整数非线性规划问题（MINLP）。针对该问题，提出了一种双层优化方法对无人机轨迹和任务卸载决策进行联合优化。首先，用一种无监督学习的h-SOM神经网络获得上层的部署。该网络是一种无导师学习方法，具有良好的自组织、可视化特性。网络根据输入的UE坐标自适应地调整权值达到聚类效果，当网络完成聚类后可以对新的UE 直接进行聚类无需重新训练。该方法相对于一般的算法减少了优化时间，因为如果增加大量UE，一般的算法需要再次迭代求解，而h-SOM 网络直接输入可以得到聚类结果，能够实时地分析UE 与UAV 的关系，从而得到UAV最优位置部署。然后，对于下层的计算卸载，使用启发式算法，即用于求解整数优化问题的IDE算法。因为在计算卸载中，包含大量的变量、参数、约束条件，运用启发式算法可以降低该部分的计算复杂度，迭代得到最佳卸载矩阵使得系统能耗最小。资源分配矩阵f的求解，则参考文献[16]，根据时间约束公式（6）令T取最大时延求每个UE分配的最小资源。此时上述双层优化方法，上层打开了下层的可行性，下层提高了上层性能评估的准确性，为解决MEC 系统的优化问题提供了一种新思路。

5 自组织特征映射网络和改进差分进化算法

本文所提出的双层优化方法如图2 所示。首先介绍联合双层优化方法的算法流程，然后具体介绍h-SOM网络和IDE算法在该问题中的应用，最后分析了算法的特点与优势。

5.1 算法流程

如图2 所示联合双层优化方法。首先用h-SOM 网络对UE 进行实时聚类从而得到UAV 的最优位置。然后利用IDE 算法迭代优化直到收敛或者达到最大迭代次数获得最终最优解。下面详细介绍h-SOM 网络和IDE算法。

5.2 改进自组织特征映射网络

自组织特征映射网络（Self-Organizing Feature Map，SOM）也称Kohonen网络。该网络是一个由全连接的神经元阵列组成的无导师、自组织、自学习网络。SOM网络能够以自适应的方式实现任意维度输入信号的聚类[19]。在本研究中使用SOM网络描述如下。

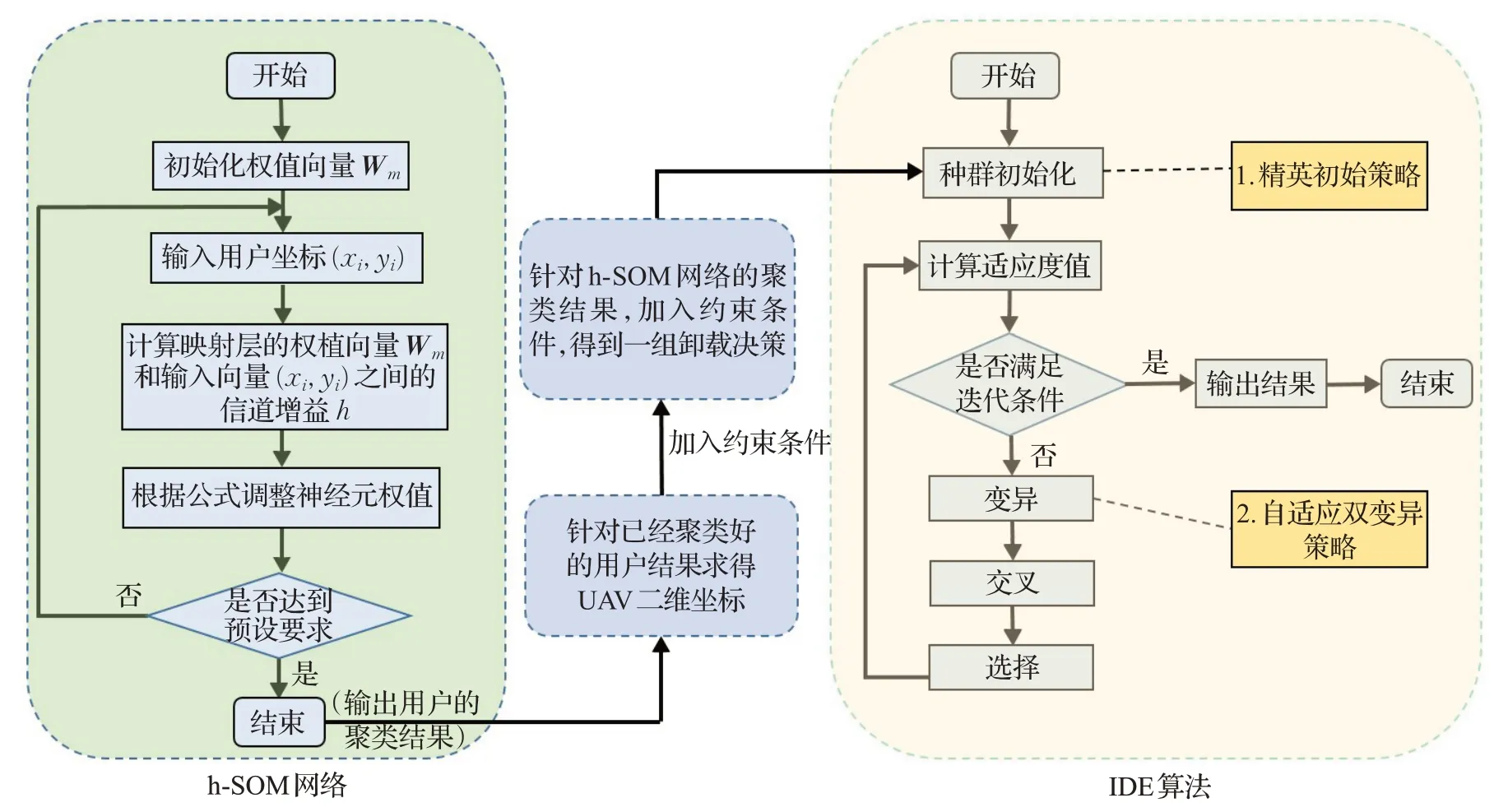
图2 算法流程

5.2.1 SOM神经网络结构

SOM 网络结构如图3 所示，由输入层和输出层（竞争层）组成。输入层神经元个数为n，输出层由m个神经元组成的二维平面阵列，输入层与输出层各神经元之间实现全连接。SOM网络能将任意维度的输入模式在输出层映射成二维图形，并保持其拓扑结构不变。网络通过反复学习输入向量使权重向量与输入向量分布趋于一致。

5.2.2 h-SOM神经网络学习算法

本文针对Q1 问题，对SOM 网络进行改进，利用信道质量h来衡量样本与网络权值之间的匹配程度。首先用矢量(xi,yi) 表示输入数据即UE 的坐标，i∈{1,2,…,k}表示数据个数，输入数据的维度与输入层的神经元一一对应。然后随机初始化输入层与竞争层神经元之间的权值Wm，Wm即为第m个UAV 的平面坐标。计算第i个输入样本zi=(xi,yi)与第m个神经元的权值Wm=(Wm1,Wm2)的匹配程度：

其中，α是小尺度衰落分量，H是无人机的高度，dim=取具有最大值h(zi,Wm)的神经元即为胜出神经元m*，然后根据下式修正输出神经元m*的权值，而其他神经元权值不变。

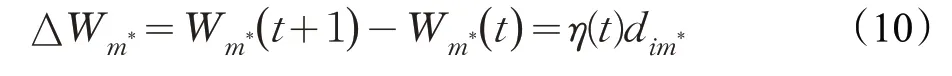
式中，0 ＜η＜1 为常数，随着时间t的变化逐渐下降。这种权值更新规则通过学习输入样本让最靠近输入样本的神经元权值向量被修正，使之更靠近，使得获胜的神经元在下一次相似的输入向量出现时，获胜的可能性会更大；而对于相差很远的输入向量，获胜的可能性将变得很小。

最后，输出网络h(zi,Wm)的权值Wm即为UAV 的最佳坐标。

5.3 改进差分进化算法

5.3.1 标准差分进化算法

差分进化算法（DE）主要用于求解整数优化问题。在DE 算法寻优的过程中分为变异、交叉和选择三个过程。其中，差分变异是DE算法的核心。首先，从父代个体间选择两个个体进行向量做差生成差分矢量；其次，选择另外一个个体与差分矢量求和生成实验个体；然后，对父代个体与相应的实验个体进行变异操作，生成新的子代个体；最后在父代个体和子代个体之间进行选择操作，将符合要求的个体保存到下一代群体中去[20]。

本工作中使用的算法详细表述如下。为简单起见，使用实数编码。在算法中，每个个体是一个卸载矩阵，个体的维度即为UE 个数，每个个体维度的范围即为J。为进一步提高DE 算法解的精度以及收敛速度，做了如下两种改进。

5.3.2 精英初始策略

精英初始策略就是把h-SOM网络聚类结果转化成一组符合约束条件的可行解代入IDE 算法中作为初始解之一。其转化思想是把h-SOM网络聚类结果依次代入公式（8）中的约束条件，若符合所有约束条件，则保留当前聚类结果，若不符合约束条件，则给定在本地执行。在IDE算法中，运用精英初始策略为算法提供了优秀的初始解。

5.3.3 自适应双变异策略

在群智能算法中，种群的搜索范围与收敛速度是两个相互制约的因素。比如，如果只扩大搜索阈值，虽然提高了种群的多样性，但在面对复杂问题时势必会影响算法的收敛速度；反之，如果单方面提高收敛速度，虽然能快速找到最优解，但算法易陷入“早熟”阶段，稳定性差。基于上述原因，在DE算法中，通常从变异策略来解决，这样既增加算法种群多样性还增加了收敛速度。本文中，使用两种变异策略，但是，如何平衡这两个变异策略，本文引入自适应算子。公式如下：

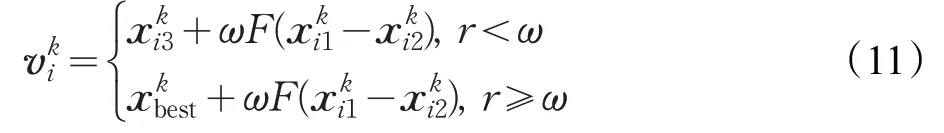
其中，F是变异因子；是第k代变异产生的新向量；分别是第k代种群中互不相同的三个向量；是第k代种群中最优适应度的向量；随机数r∈(0-1)；ω为自适应权重，公式如下：

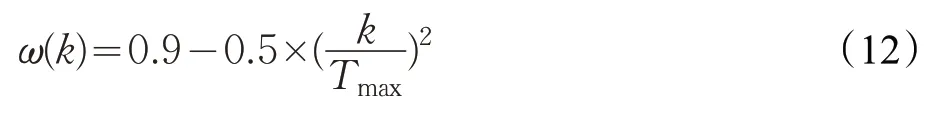
式中，k为迭代次数，Tmax为最大迭代次数，式（12）中，ω前期变化较慢，取值较大，结合公式（11），有大的概率采用第一个式子进行变异，增加了种群的多样性，维持了算法的全局搜索能力；随着迭代的进行，ω逐渐减小，有大的概率使用第二个式子能够进行精确搜索，极大地提高了算法的局部寻优能力[21]。通过这种ω权重的变化函数，能够使算法在迭代过程中不易陷入早熟收敛，这样在整个搜索过程中既高效又不失精确性。

5.4 算法的特点与优势

在移动边缘计算中，目标函数往往是一个大规模动态场景的优化问题，本文所用的联合优化算法优于传统的方法，具体表现在：（1）针对动态场景的优化问题，算法的上层h-SOM 网络是基于分类的神经网络，训练好以后能够实时进行定位和分类。传统的聚类算法例如k-means 或FCM 则需要经过迭代才能够对UAV 进行定位，不利于快速变化的动态场景。（2）在大规模应用场景下，传统的凸优化或分支界定法随着系统变量的增多，求解复杂度急剧增加，而IDE 算法的计算复杂度相对较低且具有高效的全局搜索能力，经过变异、交叉和选择三种操作同时配合h-SOM 网络聚类的初始解能够快速地迭代找到更优的任务卸载矩阵达到能耗最小。

6 仿真实验及分析

6.1 模型设置

本实验中，设定实验区域100 m×100 m，用户在该区域内随机分布。仿真平台为MATLAB R2012a，CPU为酷睿i5-7200U，内存大小为4 GB。首先给出了h-SOM网络的聚类结果图，同时与在UAV 轨迹优化中的其他经典机器学习算法进行了对比，然后评估了IDE算法的收敛性，同时与其他传统算法进行比较。通信参数设置于表1。

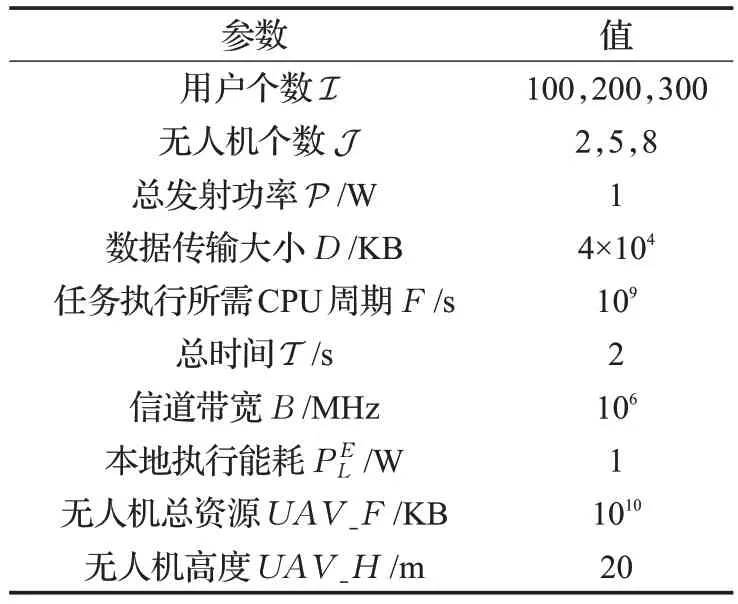
表1 参数设置

6.2 结果分析

本节中，首先给出了h-SOM 网络拓扑图与聚类结果。在h-SOM 网络中，设定样本数量为100，输入神经元个数为2。如图4（a）所示为神经元输出情况。图中小正六边形代表神经元，可以看出输出层神经元有2×2=4个，本研究中输出神经元的个数即为UAV 数量。图中的横纵坐标为六角形拓扑结构坐标。每个菱形中的线代表神经元之间直接连接，菱形中的颜色表示神经元之间距离的远近，从黄色到黑色，颜色越深说明神经元之间的距离越远。图4（b）为网络的聚类结果，图中神经元中间的数字表示每个神经元包含UE 的个数，相对来说数字越大神经元面积越大，数字越小神经元面积越小，但不会改变原始神经元的拓扑结构。

图4 h-SOM网络拓扑图与分类结果

表2 将本文算法与UAV 定位中的经典算法模糊C均值聚类（FCM）算法[22]和K-Means 算法[23]进行了能耗的比较，每个表格中有三个指标，分别是Best、Mean 和SD，用来描述算法在多次执行时的稳定性。Best 表示相同迭代次数下算法的最优解；Mean 表示相同迭代次数下所有解的平均值；SD 表示相同迭代次数下解的方差。可以看出h-SOM网络相对于其他两种算法的结果略优一些，具有最低的能耗和方差。

表2 不同算法所得UAV位置的能耗结果

基于上述相对最优UAV的部署和初始用户的聚类结果，接下来首先研究上述结果对本问题精确度的影响，如表3 所示；然后研究IDE 算法中不同参数对该算法收敛性的影响，如表4～表6所示。最后研究不同自适应算子对该算法收敛性的影响，如表7 所示。表3 所示为加入精英初始策略和不加精英初始策略的IDE 算法迭代结果。从表中可以看出，加入精英初始策略的IDE算法最优解优于不加精英初始策略最优解。因为h-SOM 网络本身是基于聚类的神经网络，在此基础上用IDE算法寻优，为算法提供了优质的初始解。

表3 不同初始值的IDE算法结果

表4 IDE算法中不同种群数量的能量消耗

表5 IDE算法中不同F 值的能量消耗

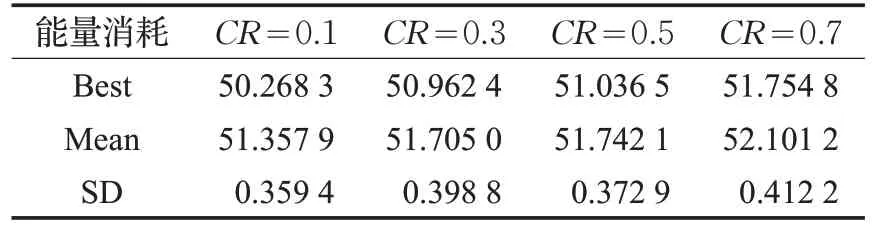
表6 IDE算法中不同CR值的能量消耗

表7 IDE算法中不同ω 值的能量消耗

然后，针对不同参数对IDE算法的影响如表4～表6所示，本实验中设置相同的初始值。在IDE 算法中，有三个重要的基本参数，即种群大小P、差分放大系数F和交叉因子CR。从表4 可以看出，所提出的算法在P=20 时保持最佳。这是因为当P很大时，小的差分放大系数会阻碍它得到最优解，同时增加迭代次数才能收敛；当P很小时，种群多样性减小。如表5 所示，能量消耗随着F的减小而变化，并且当F=1 时，收敛效果最好。这是因为小的差分系数对群体多样性的贡献比较小，而大的差分方法系数可能导致问题无解。因此，适当的差分放大系数很重要。如表6 所示，所提算法的性能随着CR的增长而下降，原因为交叉是随机的，不涉及任何已知的信息，例如最优解。设计交叉因子的目的是增加种群的多样性，而在本问题中太大反而影响结果。因此，本文对IDE算法设定P=20，F=1和CR=0.1。

接着，为了评估自适应算子对算法性能的影响，比较了固定算子与自适应算子的性能，分别取ω值0.2、0.5、0.8。如表7所示，明显看出自适应算子的优化效果较好。这是因为在迭代初期，自适应算子值大于随机数，增加种群多样性，增加全局搜索能力；后期，自适应算子随着迭代次数的增加而逐渐减小，进行局部搜索已达到迭代次数或者最优值，这种自适应算子平衡了算法全局与局部搜索提高了搜索效率。

为了验证算法的有效性，还将本文算法与贪婪算法、随机算法以及标准的DE 算法进行比较。本文所用的贪婪算法依据贪婪原则即每个UE随机将任务卸载到就近的UAV，如果就近的UAV 计算资源不足，则UE 在本地执行计算。所用的随机算法是UE随机将任务卸载到某个UAV 上，如果分配的UAV 计算资源不足，UE 将在本地执行计算。

如图5 所示，绘制了不同算法具有5 个UAV 的100到300个UE数量的能量消耗。从图5可以看出，能量的消耗随着UE的数量而增加，原因是任务数量增加，能耗增加。当用户数量分别为100、200 和300 时，图中IDE算法的能耗分别是51.241 1、140.915 6、239.262 5，同比贪婪算法降低了约10.95%、3.82%和2.24%，同比随机算法降低了约38.39%、19.87%和7.96%，同比DE算法降低了约6.98%、3.34%和1.83%。由此可以看出在UAV 数量和时延一定的情况下，图中IDE 算法的能耗最低，比最高随机算法降低了约38.39%。

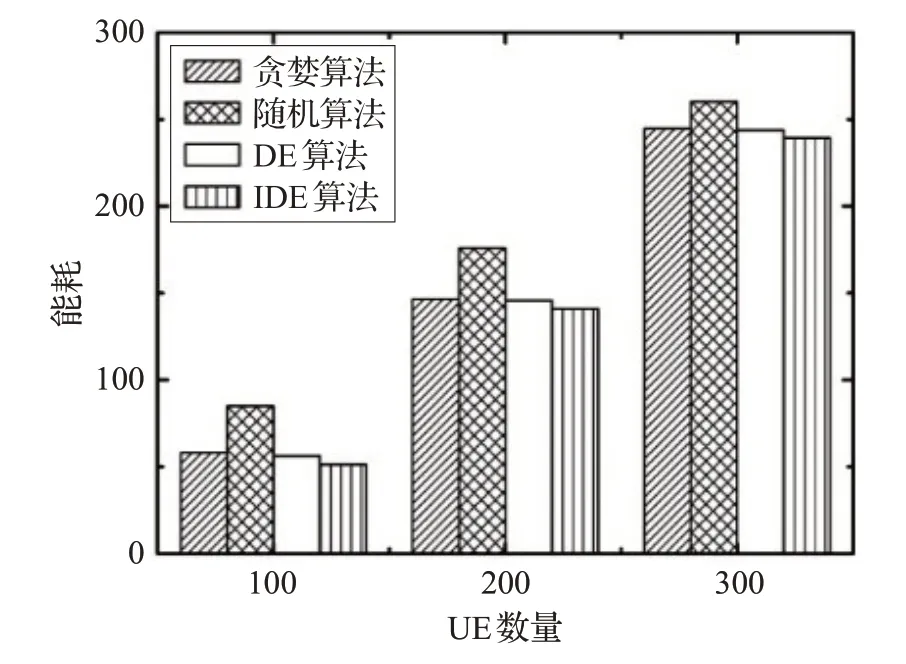
图5 贪婪、随机、DE和IDE算法在不同UE数量下的能耗图

图6 展示了不同算法具有 100 个 UE 的 2～8 个 UAV数量的能量消耗。从图6可以看出，贪婪算法、DE算法和IDE算法实现了能量消耗随着UAV数量的增加而明显下降，然而对于传统的随机算法，由于卸载是随机分配的，因此无法确保其性能，所以下降幅度不明显。当UAV 数量分别为 2、5 和 8 时，图中 IDE 算法的能耗分别是79.462 9、50.144 1、36.525 8，同比贪婪算法降低了约5.73%、9.32%和10.47%，同比随机算法降低了约12.31%、42.45%和54.33%，同比DE 算法降低了约3.37%、7.61%和6.93%。由此可以看出在UE数量和时延一定的情况下，图中依然是IDE 算法的能耗最低，随机算法的能耗最高。可以看出最高能耗和最低能耗相对于图5 的能耗还要降低得多，因为图6 实验中无人机数量相对较多，可以将更多的任务合理地在无人机上进行卸载。

图6 贪婪、随机、DE和IDE算法在不同UAV数量下的能耗图

图7 展示了不同算法具有 100 个 UE，5 个 UAV 的2～6 s时间延迟的能量消耗。在图7中，可以明显看到随着延迟的增大，系统的能耗只做出了微小的改变，但是本文所提的IDE 算法仍然保持最低能耗。这是因为该算法在搜索方面功能强大，不易陷入局部最优点，进而获得更优的解。当时延分别为2 s、4 s 和6 s 时，图中IDE 算法的能耗分别是50.456 9、45.243 2、40.925 8，同比贪婪算法降低了约8.91%、7.13%和9.51%，同比随机算法降低了约42.49%、46.17%和50.67%，同比DE 算法降低了约6.92%、4.22%和5.38%。可以看出在UAV 数量和UE 数量一定的情况下，图中能耗最低的依然是IDE算法，最高是随机算法，而贪婪算法和DE算法的能耗相对于IDE算法的能耗略高些。

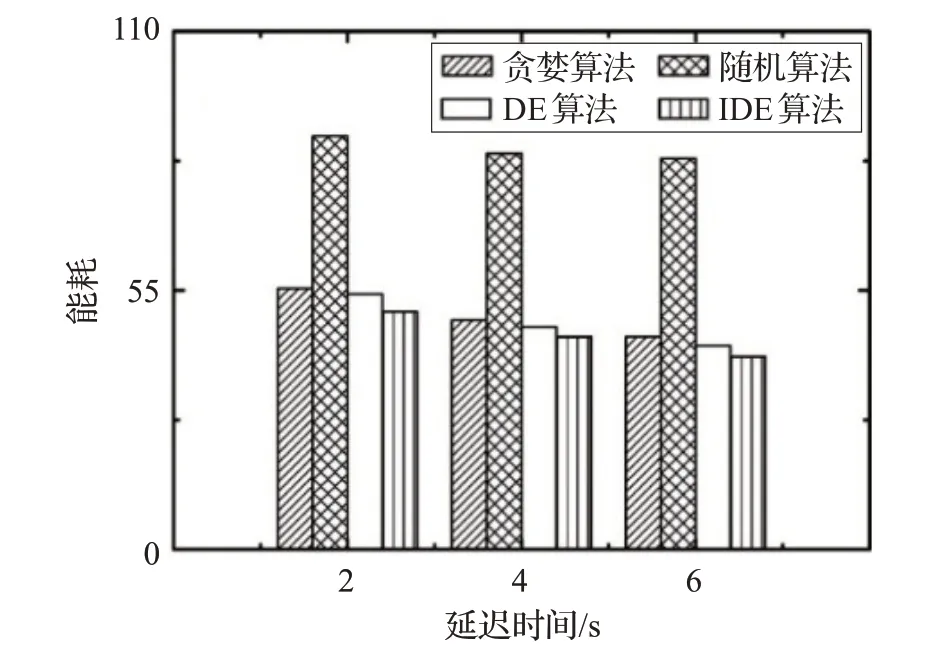
图7 贪婪、随机、DE和IDE算法在不同时延T下的能耗图

从图5、图6 和图7 中可以看出，本文所提的联合双层优化方法即h-SOM 网络和IDE算法的性能优于其他两种传统算法。对于传统的随机算法，UE 随机做出决定，可能导致UE 卸载到距离自己较远的UAV 上，在这种情况下，传输能量消耗就变得异常大，同时对于卸载UE 有可能变得无效，因此它保持最高的能量消耗。贪婪算法、标准DE算法和IDE算法执行计算分配，可以控制UE的卸载数量，从而为UE节省能量，所以这三种算法的表现优于随机算法。贪婪算法在求解该问题时基于一定的贪婪策略即每个UE把任务卸载到离自己最近的UAV 上，这样虽然减少了UE 在传输过程中的能耗，但并未全局考虑UAV 的计算资源限制。DE 算法是一种基于全局搜索的群智能算法，它将差分操作迭代地应用于群体，直到达到最优解，所以标准DE算法比贪婪算法有更好的性能。在DE算法的基础上引入精英初始策略和自适应双变异策略，每次迭代产生随机数与自适应算子进行比较采取不同的变异策略，使得算法在迭代初期保持解的多样性，在迭代后期局部搜索更加准确，提高算法的精确度。因此，IDE算法比其他三种算法的性能优越。

6.3 复杂度分析

表8比较了h-SOM网络和FCM及K-Means算法的计算时间。从表8 可以看出，本文所用的h-SOM 网络由于初始时需要进行迭代训练，训练时间高于FCM 和K-Means算法，但是训练好后的h-SOM只需要执行神经网络的前向计算就可以得到分类结果，其计算复杂度远低于FCM 及K-Means 算法，适合求解实时的动态优化问题。

表8 不同算法的时间消耗s

图8展示了IDE算法与贪婪算法、随机算法以及标准的DE算法在不同UE数目下计算时间的对比图。从图8中可以看出，贪婪算法和随机算法的计算复杂度相对较低，但是根据前面的实验结果，两种方法解的质量均不高。DE算法和IDE算法均具有较好的全局搜索能力，计算复杂度相当，但是由于IDE 算法引入了精英初始策略和自适应双变异策略，所以IDE算法能够较快收敛，计算时间更少，结果更优。因此，相对来说，本文所用的算法整体性能更优。

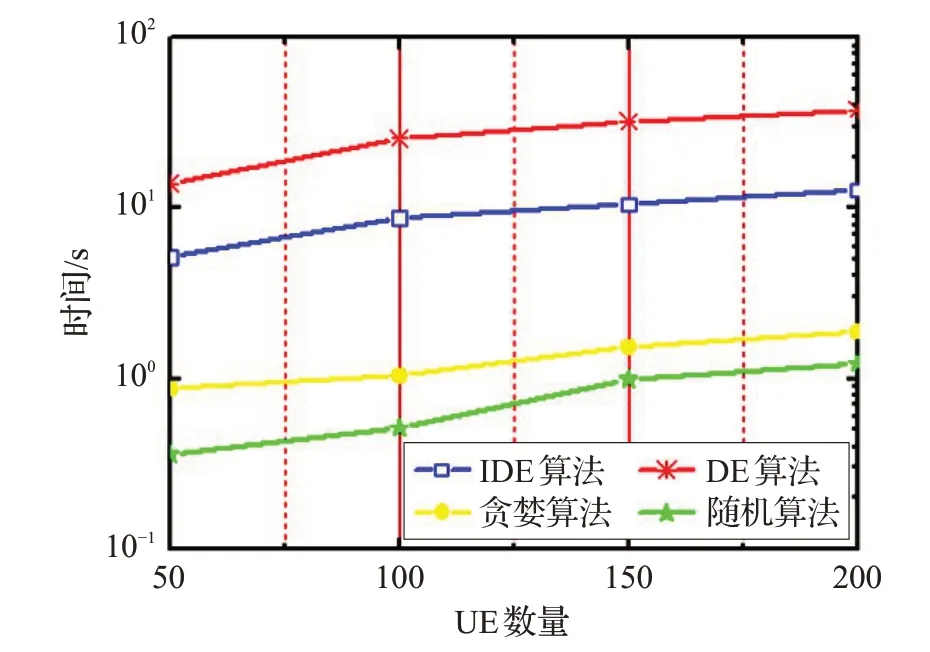
图8 贪婪、随机、DE和IDE算法不同UE下的时间消耗图

7 结论

本文研究了多用户-多无人机MEC 系统的计算卸载方案，通过用多个UAV 提高传统MEC 系统的性能。在该系统中需要联合优化UAV 的位置部署和计算卸载。一般方法来解决这一联合优化问题时，将面临两个问题：混合决策变量和解空间较大，同时忽略了UAV的部署和任务卸载之间的关系。本文提出的这种双层优化方法，以UAV的部署为上层优化问题，任务卸载为下层优化问题的两层优化方法。在上层中，用h-SOM 神经网络，根据UE的位置求解UAV的最佳部署。该方法不仅减少了计算时间，而且针对新用户能够快速聚类，无需重新求解。接着，IDE 作为下层优化算法，针对多变量，多目标优化问题能够提高全局搜索能力，自适应地调整卸载策略达到最优。

最后，针对本文所提算法性能进行了仿真实验，并通过各种性能指标验证了本文算法的有效性。