基于梳状扇形孔周期性结构的纵-扭复合模态超声振动系统

林基艳，林书玉

(1.陕西师范大学物理学与信息技术学院，陕西西安710119；2.榆林学院信息工程学院，陕西榆林719000)

0 引 言

纵-扭复合模态的超声振动系统因为符合高效率、高精度、高可靠性的现代科技工业和技术的发展要求，受到越来越多的重视[1]。虽然纵-扭复合型超声加工方式得到了世界的公认，但在其设计、研究、加工制造等方面没有形成系统的、完善的理论体系[2]。针对上述情况，国内外学者对有关问题都进行了积极的理论研究与实验分析。

螺旋状麻花钻头型变幅杆可以产生纵-扭复合振动，但由于变幅杆的结构复杂，理论计算及设计极为繁琐，不利于工程技术中的广泛应用[3]；也有研究者利用切向极化的压电陶瓷圆环产生扭转振动，但由于切向极化压电陶瓷元件的极化、加工工艺复杂以及换能器的纵向与扭转振动很难实现同频共振等的限制，导致换能器的功率容量、振动性能受限，不利于大功率的超声应用[4]。日本学者在超声马达的研制中，提出了一种纵-扭复合振动模式超声换能器，利用超声变幅杆上的斜槽实现纵-扭复合[5]；Karafi等[6]设计了一种纵-扭磁致伸缩超声换能器，通过将径向磁场和周向磁场复合而成的螺旋磁场施加到磁致伸缩变幅杆上，产生径向振动和扭转振动，但纵-扭效果均不理想；林书玉[7]对斜槽式纵-扭复合超声振动系统进行了研究，指出因为振动传递到斜槽时产生的切向力导致系统产生扭转振动，并推导出纵-扭振动的机械转换系数，分析了斜槽参数对振动系统的频率的影响。皮钧等[8]研究了斜槽式纵-扭超声振动装置，着重分析斜槽圆环变幅杆的纵-扭转化原理；唐军等[9]研究了一种新型的贴片式纵-扭复合振动系统，通过调整压电陶瓷与换能器轴的轴向角度，使系统产生纵-扭复合振动。

目前，很多研究都倾向于采用斜槽结构实现单激励的模式转换型纵-扭换能器，这种方法实现起来较为简单，但斜槽式纵-扭振动系统普遍存在扭转分量较小、转化效率低等缺点[10]。基于此，本文提出了基于周期性结构的复合模态超声振动系统并对其进行研究，该系统由纵向振动夹心式压电陶瓷换能器、圆锥形变幅杆以及带有梳状扇形孔的斜槽式振动体三部分组成，驱动部分采用纵向振动的夹心式压电换能器，振动输出部分则是采用梳状扇形孔的斜槽式振动体。通过有限元分析软件对设计的结构进行了必要的分析和验证，通过仿真分析表明，该复合模态超声振动系统扭转分量大，转化效率高。

1 周期性结构纵-扭复合模态超声振动系统的原理和设计

1.1 模态转换原理

周期性结构纵-扭复合模态超声振动系统是利用轴向极化的压电陶瓷片产生纵向振动，当纵波传递到斜槽位置时，由于斜槽的作用，变幅杆的输出端会产生两种振动：纵向振动以及由剪切分力产生的扭转振动[11]。其原理示意图和产生扭转振动部分的振动体的截面如图1所示。

图1 带有梳状扇形孔和斜槽的纵扭振动转换体Fig.1 The longitudinal-torsional vibration converter with comb sector holes and skewed slots

图1中斜槽处的力F被分为两部分：法向力FL和剪切力Fγ，二者的关系可表示为[7]

式中：θ为斜槽和变幅杆轴线之间的夹角。基于机械振动理论，法向力使得振动系统产生纵振，剪切力则使系统产生扭转振动。剪切力在变幅杆前分界面处的扭矩M可由式(3)表示[7]：

式中：sd为圆环的截面积，表示为

式(3)、(4)中：R1和R2分别为圆环的外、内半径；R3为中心圆的半径；r为变幅杆圆筒内任意处的截面半径；dsd为微分元面积；τ为分界面上单位面积的剪切力，因此，由以上可知，单位面积的剪切力τ可表示为[7]

将式(5)代入式(3)积分后，便可得到如下公式：

根据以上分析可知，因为斜槽的存在，振动体中的振动形式由一维的纵向振动转换为二维纵-扭复合振动。

1.2 梳状扇形孔周期性结构的设计

扭转振动主要由两种方式来实现：振动模式转换和切向极化的压电陶瓷晶堆的振动。第二种方法由于工艺复杂、电击穿、功率容量等问题，很难研制大功率高性能的振动系统[12]。因此，本文采用第一种模式转换的方式。

模式转换常用的方法有开斜槽和开螺旋槽，但开螺旋槽的方法结构复杂，理论计算及设计极为繁琐。因此本研究采用了在振动体上开斜槽的方法来实现纵-扭复合模态的超声振动。其优点是结构简单，但研究发现，该方法产生的扭转分量较小，转化效率较低[13]。为了增大扭转分量，提高转换效率，本设计采用了梳状扇形孔周期结构振动体。

该梳状扇形孔周期结构可近似等效为弹簧-摆模型，即每个扇形片可以看作一个具有剪切和弯曲刚度的弹簧，其中每个扇形片在振动中所起的作用也不同，有的可以看作剪切弹簧，有的可以看作拉压弹簧，有的同时起剪切和拉压的作用，扇形片的剪切变形增加了系统的扭转分量[14]。整个梳状扇形孔周期性结构如图2所示。

图2 梳状扇形孔周期性结构和振型图Fig.2 The periodic structure and its vibration mode shape of comb sector holes

2 有限元分析

周期性结构纵-扭复合模态超声振动系统由夹心式换能器、圆锥型变幅杆以及梳状扇形孔周期结构振动体组成。根据一维纵向振动理论，初始先按谐振频率为 20 kHz来设计全波长结构的超声振动系统，其中夹心式压电陶瓷换能器为半波振子换能器，圆锥形变幅杆和梳状扇形孔周期结构振动体二者整体为半波振子。换能器由前盖板、压电陶瓷晶堆和后盖板三个部分组成，前后盖板的材料均为铝，密度ρ=2 700 kg·m-3，弹性模量E=69 GPa，泊松比 σ=0.33，压电陶瓷晶堆选择 PZT-4，密度 ρ=7 500 kg·m-3，弹性模量 E=64.5 GPa，泊松比 σ=0.32。根据以上分析计算，设压电陶瓷厚度为 6 mm，两片压电陶瓷的半径为 25 mm；前盖板长度为35 mm；后盖板长度82 mm。对圆锥形变幅杆，初始设置大端的底面半径为 25 mm，顶面半径为20 mm，长度为58 mm。梳状扇形孔周期结构振动体的初始半径设置为20 mm，长度71 mm。

图 3为初始周期性结构纵-扭复合模态超声振动系统Comsol模型图和尺寸图，图4为振动体的结构尺寸图。

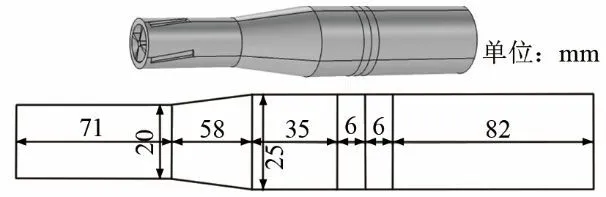
图3 初始纵-扭复合模态超声振动系统模型、尺寸图Fig.3 Model and dimension diagram of initial longitudinaltorsional composite modal ultrasonic vibration system

图4 初始振动体结构尺寸图Fig.4 Dimension diagram of initial vibration body structure

2.1 周期性结构参数对振动系统谐振频率的影响的分析

超声振动系统中的一个重要的参数是谐振频率，谐振频率会随着振动系统结构的变化而改变，即梳状扇形孔周期性结构的存在，可以影响系统的谐振频率。

因此，本文仿真分析了周期性结构参数对振动系统频率的影响规律，这里的周期性结构包括两种——斜槽和梳状扇形孔。斜槽参数主要有斜槽的倾角θ、长度L、宽度W、深度H和离圆锥段距离S，离辐射面的距离S1；梳状扇形孔参数主要有扇形片的中心角度数φ、半径R2和内核圆半径R3。斜槽和梳状扇形孔参数示意图如图5所示，仿真结果如图6～13所示。

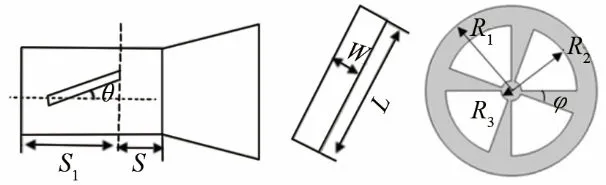
图5 斜槽和梳状扇形孔参数示意图Fig.5 Schematic diagram of the parameters for skewed slots and comb sector holes

图6 斜槽倾角对频率的影响Fig.6 Influence of slot inclination on system frequency

图7 斜槽长度对频率的影响Fig.7 Influence of slot length on system frequency

图8 斜槽宽度对频率的影响Fig.8 Influence of slot width on system frequency

图9 斜槽深度对频率的影响Fig.9 Influence of slot depth on system frequency

图10 斜槽离圆锥端距离对频率的影响Fig.10 Influence of the distance of slot from conical end on system frequency

图11 扇形中心角度对频率的影响Fig.11 Influence of sector central angle on system frequency

图12 扇形片半径对频率的影响Fig.12 Influence of sector radius on system frequency

图13 内核圆半径对频率的影响Fig.13 Influence of the radius of inner circle on system frequency

通过图6可以发现，当其他参数不变时，随着斜槽倾角θ的增大，以纵振为主的谐振频率逐渐减小，当θ≥70°时，随着θ的增大，以纵振为主的谐振频率逐渐增大，而以扭振为主的谐振频率变化趋势与之相反。从图7可知，当其他参数不变时，以纵振为主的谐振频率随着斜槽长度 L的增大先增大，后减小，然后再增大；而以扭振为主的谐振频率随着斜槽长度L的增大先减小，然后趋于平稳。从图8可知，纵振和扭振为主的谐振频率皆随着斜槽宽度W的增大而增大。从图9可以看出，纵振为主的谐振频率随着斜槽深度H的增大先增大，后减小；而扭振为主的谐振频率随着H的增大先变化平缓，后减小。从图 10可以看出，纵振为主的谐振频率随离圆锥段距离S的增大而减小；而扭振为主的谐振频率随S的增大而逐渐增大。

梳状扇形孔参数对谐振频率的影响如图 11～13所示。从图11可以看出，纵振为主的谐振频率随扇形片中心角度φ的增大而减小；而扭振为主的谐振频率随着φ的增大先减小后变化平缓。从图12可以看出，纵振为主的谐振频率随着扇形片半径R2的增大而增大；而扭振为主的谐振频率随着R2的增大先变化平缓后减小。而从图13则可以看出，纵振为主的谐振频率随着内核圆半径R3的增大而减小；而扭振为主的谐振频率随着R3的增大而逐步增大。

通过 Comsol派生值的表达式计算发现，合理选择换能器的前后盖板长度、复合变幅杆长度及振动体参数，可以有效地增大纵、扭振振幅，位移旋度和剪切应力以及法向应力等，提高纵-扭转化能力。因此，综合考虑周期性结构对超声振动系统谐振频率和Ux、Vy、Wz以及位移旋度、剪切应力和法向应力等性能指标的影响(Ux、Vy、Wz分别代表节点随时间和位置变化的位移响应，从Ux、Vy可分别得到x、y方向的位移振幅，从Wz则可以得到变幅杆z方向即纵振振幅，位移旋度x、y矢量则表示物体转动时在x、y方向的转动位移，位移旋度越大，扭转分量越大；垂直于剪切面的单位面积上受到的内力分量，称为法向应力，相切于剪切面的单位面积上受到的内力分量称为剪切应力)，最终设定了换能器、复合变幅杆以及复合变幅杆振动体结构的各部分尺寸，如图14、15所示。

图14 纵-扭复合模态超声振动系统最终模型、尺寸图Fig.14 Final model and dimension diagram of longitudinaltorsional composite modal ultrasonic vibration system

斜槽的长度为30 mm，宽度为2.5 mm，深度为5 mm，与圆柱端y轴向成80°(与z轴成10°)。此时系统的剪切应力、法向应力、振幅、位移旋度相对较大，性能最好。

图15 振动体结构最终尺寸图Fig.15 Dimension diagram of final vibration body structure

2.2 模态分析

模态分析的目的是确定结构的固有频率和振型[15]。为简化模型，忽略预应力螺栓的影响。利用Comsol进行模态分析，搜索频率范围为5～20 kHz，通过观察模态振型可知，系统在f=7 896、11 336 Hz时，振动形式是扭转振动为主的纵扭复合振动；f=12 226、18 750 Hz时，振动形式是纵向振动为主的纵扭复合振动，振型图如图16所示。

图16 纵-扭复合模态超声振动系统振型图Fig.16 Diagrams of vibration mode shape of the longitudinaltorsional composite modal ultrasonic vibration system

2.3 周期性结构对振动系统性能影响的分析

本文将复合变幅杆圆柱端设计为梳状扇形孔周期性结构，根据前面的分析可知，该结构可以有效的增大扭转分量。为了更加形象地看到效果，本文将无周期性结构和有周期结构的系统进行仿真对比(其它参数均相同)，二者的模型如图17所示。

图17 超声振动系统变幅杆圆柱端有或无梳状扇形孔周期结构的模型对比图Fig.17 Comparison of the model of ultrasonic vibration system with or without the periodic structure of comb sector holes at the cylindrical end of horn

选取剪切应力、法向应力、振幅、位移旋度作为评价指标进行对比。对比的效果如表1、2所示，数值越大，系统的性能越好。因为振型较多，因此这里只选取部分振型进行研究。

从表 1、2可以看出，周期性结构的各项性能指标均优于非周期性结构。

表1 有无周期结构的系统扭转振动的指标对比表Table 1 Comparison of the indicators of torsional vibration for the system with or without periodic structures

表2 非周期结构和周期性结构纵振指标对比表Table 2 Comparison of the indicators of longitudinal vibration for the system with or without periodic structures

3 结 论

基于斜槽的纵-扭复合模态超声振动存在扭转分量小、转换效率低等问题，针对此问题，本文设计了基于周期性结构的纵-扭复合超声振动系统，通过在复合变幅杆上设置梳状扇形孔和斜槽，得到扭转分量大的纵-扭复合超声振动系统，并使用有限元分析方法对系统的振动模态、结构和影响系统性能的参数进行了分析研究。梳状周期性和斜槽的设计可为其它纵-扭复合振动超声系统提供参考，具有一定的指导意义。