“变式训练”在数学情境教学中运用策略的研究

王年

摘要：初中数学教学中，采用“变式训练”策略，创设不同的问题情境，有助于激发学生的探究热情和探究兴趣，营造良好的课堂氛围，提高课堂教学效率和深度.因此，教师应根据具体教学内容和问题情境，立足具体数学问题和思维深度，及时进行“变式训练”，使学生在掌握数学知识本质的基础上，灵活运用所学，提升数学学习的兴趣和素养以及解决问题的能力.

关键词：初中数学 情境教学 变式训练

随着素质教育和课堂教学改革的逐步落实和深化，传统教学方法逐渐被抛弃和改良.教育工作者积极探寻高效有趣的教学方法，其中“变式训练”就是其中一种.变式训练不仅能提高学生对所学知识的兴趣和热情，而且能切实提高学生运用所学知识解决实际问题的能力.

一、“变式训练”的背景和意义

初中数学教学中，“变式训练”指将所要研究的数学问题融入到同问题情境中，通过提出不同的渐进的问题，或对情境内容作局部改变提出不同的问题，要求学生运用所学知识进行渐次解答，是“一题多变”的演变和升华.在初中教学改革和课堂实践中，运用“变式训练”意义深远.

其一，促使学生加深理解所学数学知识及其应用范围.初中数学知识存在知识点多，涵盖范围广等特点，仅仅靠死记硬背是不够的，掌握的关键在于深入理解，融匯贯通.对初中生而言，有些数学知识比较抽象，直接理解的难度比较大，因此教材对各部分数学知识点都进行了情境化处理.教材将数学知识融入到相应具体的情境中，一方面，可使学生充分认识到数学来源于生活，激发学生努力学习的兴趣和积极性，另一方面，也使学生清楚地认识到，来源于生活的数学知识又要如何运用到生活中去，运用所学的数学知识来解决实际生活中的问题，以及在解决实际问题时如何用数学的思维去进行思考及运用数学的方法去解决问题.

其二，提高学生灵活运用知识的能力和解决问题的水平.灵活运用所学知识是教育工作者对学生的重要要求，也是素质教育积极提倡的.初中数学教学过程中，如何引导学生活学活用数学知识已经成为数学教师的重要任务及衡量教育教学水平的重要指标.“变式训练”除对学生所学知识考查较为全面和深入外，通过“变”情境，“变”问题，“变”思维，能很好地锻炼和提高学生灵活运用所学知识解决问题的能力，促进学生比较化归、总结规律、融会贯通、举一反三，切实提高学生的学习质量与效率和解决问题的素养和能力.

其三，提升学生的创新意识和创新能力.在数学知识的学习过程中，提高学生的创新意识和创新能力，有助于学生综合数学素养的全面提升，采用和强化“变式训练”教学方法和策略，既可以通过教师对情境和问题进行改变，也可以引导学生去尝试着创新情境和问题，使学生参与到数学问题情境的创造中来，然后运用所学知识进行探究和解答，更能提高学生学习的主动性和能动性，变学生的“要我学”为“我要学”.

二、“变式训练”的流程及原则

初中数学“变式训练”教学策略的选择和应用中，由于学生是学习的主体，创设符合学生认知特点、年龄心理特点，及感兴趣的教学情境，能更好地激发学生探究的欲望、思考的热情和参与的积极性.“变式训练”的整体流程可分为两个层面五个环节.

实践表明，在运用“变式训练”教学策略并采用以上流程和环节时，应注重遵守以下原则：

（1）“变式”情境趣味性.

众所周知，初中数学知识点、概念、公式、性质等各种公理、定理、推论较多，学习起来较为枯燥，因此，为避免“变式训练”中学生产生枯燥感，创设数学情境时应注重趣味性，使学生自主探索、互动讨论、主动化归来认识问题、分析问题、解决问题，因此，教师平时应注重收集学生感兴趣的话题或社会热点，将其与数学知识良好结合，创设出新颖、有趣、有助于提高学生兴趣的数学知识和问题情境.

（2）学生参与“变式”积极性.

初中数学运用“变式训练”时，应采取措施激发学生的参与主动性和积极性，如此才能获得事半功倍的教学效果，所以，一方面，教师应与学生积极互动，拉近与学生间的距离，活跃课堂气氛的同时，逐步引导学生思考，发散思维.另一方面，教师应注重及时总结正确有效的教与学的方法，以便更好地调动学生参与的主动性和积极性.

（3）知识“变式”连贯性.

初中数学“变式训练”应围绕知识情境展开，“变”应具有一定的整体性、递进性、连贯性，要求教师对整个初中数学知识有整体和全面的把握，注重在知识的重叠处、交汇点来设置“变”的问题.同时，为使学生感受到学习的成就感，设置的问题应由易到难、层层递进、环环相扣、确保连贯，避免难度过大，使学生产生畏惧心理，挫伤学生参与的主动性和积极性.

（4）问题“变式”针对性.

初中数学“变式训练”运用时应遵守针对性原则.一方面，创设的情境应立足学生原有知识结构和特点，创设与学生生活息息相关的教学问题情境，如此才能使学生感受到数学知识的妙用及重要性，从而更加自觉、努力地投入到学习中.另一方面，创设数学情境时应注重分析整体教学目标，明确教学的重点和难点，使“变式训练”能更好地为实现教学目标服务.

三、“变式训练”的运用策略

初中数学教学中，应用“变式训练”时，为获得良好的教学效果，教师应注重总结与探寻相关的运用策略.“变式训练”的实质：“一题多变”“一题多解”“多题一法”.以“一题多解”为例.

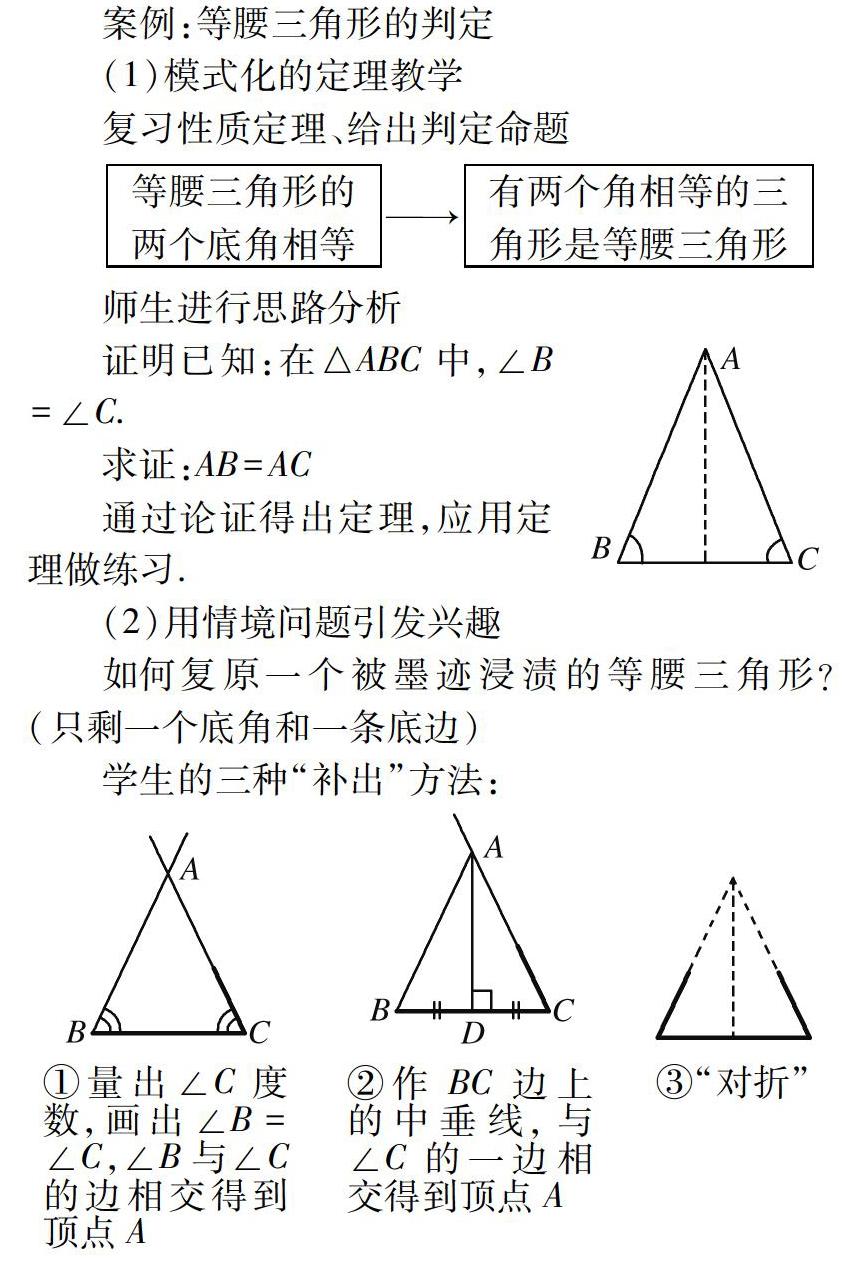
案例：等腰三角形的判定

（1）模式化的定理教学

复习性质定理、给出判定命题

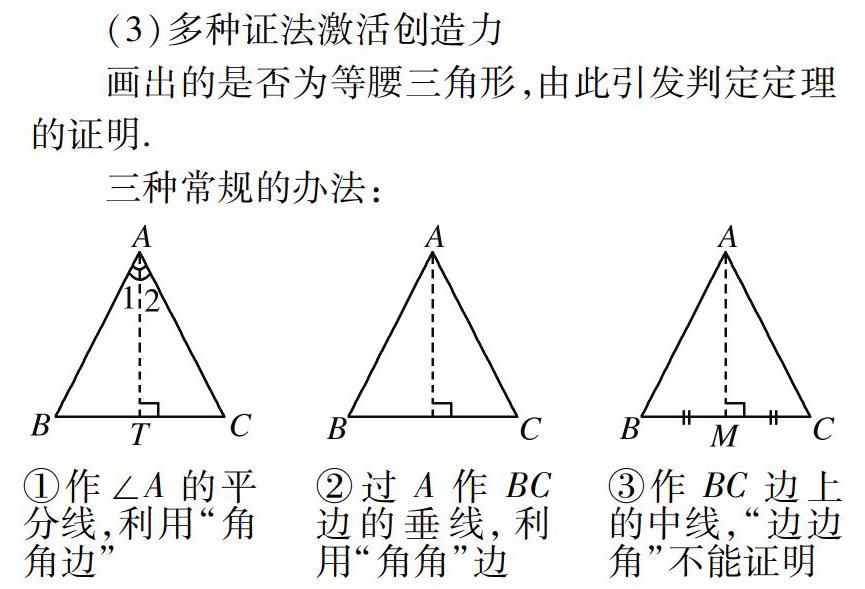
通过以上一系列的变式、探究活动，不仅巩固了等腰三角形判定和性质，更重要的是让学生在类比、联想、合作、交流中，以一个研究者的身份去探索，去发现，去品味成功的愉悦，去学习探求真理的方法，有效地培养了学生的科学创新精神.

四、初中数学“变式训练”运用注意事项

由于初中数学“变式训练”的运用对教师的综合素质要求较高，为获得预期的应用效果，首先要求教师应做好“变式训练”应用研究，多进行实践，总结与掌握“变”的策略与技巧，尤其要灵活运用学校拥有的各种资源，如多媒体技术，制作与创设各种有趣的母题情境，提高学生讨论与思考的热情.同时，做好初中数学教学内容分析，确保创设的情境与数学知识良好融合.

其次要积极参与听评课活动.为提高“变式训练”应用和实施水平，教师应抱着持续学习的心态，注重参与听评课活动，借鉴其他教师的成功做法.可在课下询问学生，认真听取学生反馈，了解“变式训练”应用中存在的不足，积极采取有效措施优化相关教学环节.

第三，教师还应积极参与教科研活动.通过分享“变式训练”的应用经验，和其他教师一起积极讨论优化“变式训练”有效的途径，尤其注重将新的思路、方法，融入到“变式训练”教学活动中，充分发挥“变式训练”在初中数学中的作用.

从近年来各地课改数学中考命题的趋势来看，对于学生思维的广度、深度的要求有所增加，试题比较注重学生探究能力的考查.因此，在平时教学中我们可以从一些最简单的命题入手，设计一些有层次、有梯度、要求明确、题型多变的例题、习题，训练学生不断探索解题的捷径，使思维的广阔性得到发展;对于一些容易混淆的数学的概念、法则，可以将它们进行“变式数学”促使学生作出客观的评价，提高辨别是非的能力，提高思维的批判性.当然，在实际教学中如果能注重教材中的重难点，教师的能力水平以及学生的认知能力和特点这三方面的话，“变式训练”将会发挥出很大作用.