让学生离“π”更近一些——《圆的周长》教学思考和实践

浙江省余姚市黄家埠镇中心小学 陈建国

圆是小学生第一次接触的曲线图形，其周长计算教学也自然成为教学难点。同时，圆周率概念相对抽象，虽然可以运用“π”来进行计划，但学生要真正理解“π”则存在较大难度。为了让学生理解“π”的本质，在“圆的周长”中，首先利用正六边形和正方形的周长，推理猜测圆的周长与直径的比值，让学生在无形中接近“π”；在实践操作中计算圆的周长与直径的比值，感受圆周率的近似值，并在圆周率的历史发展中全面认识“π”；同时，还要指导学生就直径、半径与周长的变化规律进行观察与分析，感受、体验周长与直径的比值是一个固定值，感悟“π”的特点；最后在钢琴曲与图集中，欣赏“π”与艺术的融合之美。让学生在这些过程中，一步步接近这个看不见、摸不着的“π”。

一、推理猜测中接近“π”

猜想是展开数学思维过程的重要方法。直接猜测圆的周长与直径的关系缺少了理论依据，为了引导学生合理展开猜想，借助正方形和正六边形两个图形的周长与直径的关系，合理地推理，大胆地猜想是解决问题的 源泉。

【片段一】

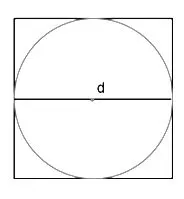
师：圆的周长与直径究竟有什么关系呢？老师请了正方形来助场。

师：你知道了什么？

生：正方形的周长就是4d。

生：圆的周长比正方形的周长小。

生：圆的周长不到4d。

生：圆的周长与直径的比值肯定不到4。

师：这合理的推理真出色。

（板书：圆的周长/直径＜4）

师：正方形让我们对圆的认识更近了一步，老师还要请出一个图形。（师出示正六边形）你知道了什么？

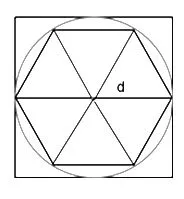
生：六边形的周长要比圆的周长大。

师：正六边形的周长与直径d 有什么关系呢？

生：正六边形是直径的3 倍。

师：为什么？

生：每个三角形都是等边三角形，因为它的顶角是60°，两边是圆的半径，那么六边形每条边都是圆的半径，所以周长是直径的3 倍。

师：那么圆的周长与直径是几倍关系了吗？

生：我觉得是3 倍多。（板书：3 ＜ 圆的周长/直径＜4＝ ）

在推理过程中先将正方形的周长与圆的直径进行结合，再将两者的周长进行对比分析，顺势将圆的周长与直径的比与“4 倍”进行结合分析。在研究的方法上，教师引导学生掌握了学习方法，也明确了探究思路，为进一步利用正六边形进行研究做好准备。由于有了正方形辅助比较的经验，在正六边形与圆的周长的比较过程中，学生就很快将正六边形的周长与圆的直径联系起来，再将圆的周长与六边形的周长比较，由此建立圆的周长与直径的联系，进一步得到了圆的周长与直径的比值范围。

二、实践验证中认识“π”

实践出真知，学生在观察、实验的基础上，在教师的引导下通过猜测、计算、推理、验证等活动完成对“π”的初步理解。但动手操作必会出现误差，以及“π”无限不循环的特点，最后要用相关资料介绍“π”。为了让学生对“π”有更深刻的了解，利用多媒体，以时间轴的形式将圆周率的发展历史展示出来，让学生在动手实践和历史验证中认识“π”。

【片段二】

（每个学具袋里装三个不同大小的圆，一条软尺，一根线，每组圆的大小随机，共4 种圆）

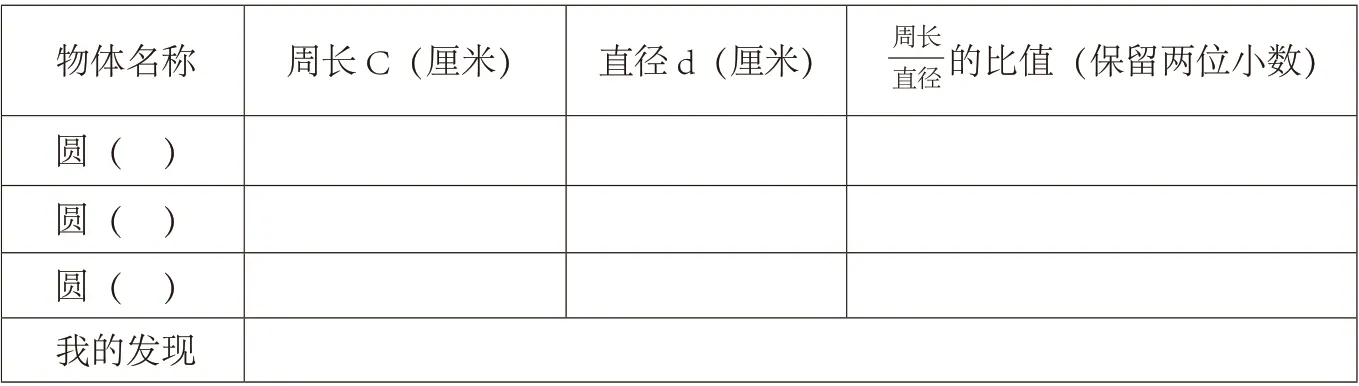
表一

实验要求（完成活动一）：

①同桌合作，用你喜欢的方法测量出圆的周长（精确到0.1），将直径和周长填入表格（见表一）。

②用计算器计算出周长和直径的比值，得数保留两位小数。

③观察表格，你发现了什么？记录在“我的发现”一栏中（见表一）。

【片段三】

师：祝贺大家，你们刚刚做了一个数学家们曾做过的实验，你们得出的结论和数学家一样。实际上，这是一个固定的数，叫做圆周率。我们一起来看看圆周率的发展历史。（播放一段视频）

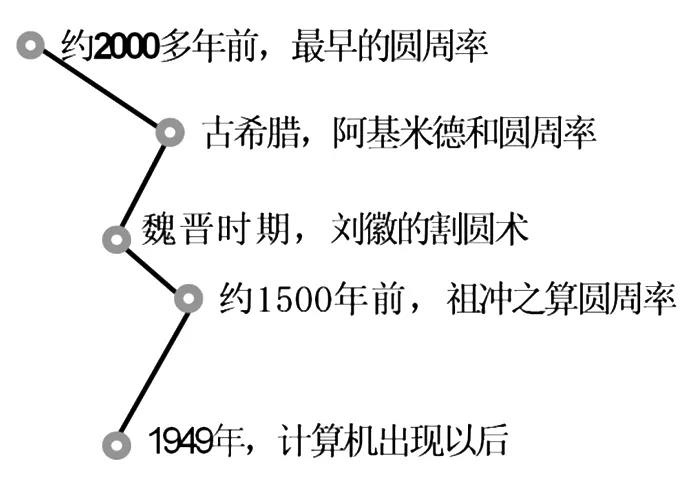
正因为有之前的推理以及帮助，引导学生明确了比值范围，教师则可以在具体细致的指导下，学生的操作可行性变得更高了，商与3.14 越接近，就越有说服力，让学生的结论离那个虽在眼前却又抓不准的“π”更近一步，也对“3 倍多一些”中的一些有较深刻、较准确的把握。最后，利用微视频的形式呈现圆周率的发展史，清晰直观地把知识的形成过程呈现给学生。实践操作、历史验证，让学生在圆周率的发展历史中离“π”更近了一步。

三、观察比较中感悟“π”

学生已掌握圆的周长计算方法，但记住周长公式并不是唯一目的，更重要的是理解周长公式的本质，理解半径、直径与周长的关系和变化规律。教师要指导、鼓励利用既有素材进行对比性观察与分析，使之能够在思维冲突过程中，不断进行正误的甄别，理解该知识体系的本质属性，促使学生能够自主发现该知识体系的数学规律，为培养、提高学生的数学思维奠定基础。

【片段四】

师：这个圆的周长与直径的比值应该是几？

（根据学生的回答，擦除表格中第四列中的数据，改成3.14）

师：（擦除“周长”一列数据）你能算出准确的周长吗？怎么算？

生：直径乘“π”（3.14）。

师：正确！同学们，你们再自己计算一个每个圆的周长是多少？（记录数据）

师：观察、分析表格中数据（第二列和第三列），看看周长、直径都有怎样的变化规律？

生：直径由2cm 变成4cm，增长两倍……直径增加几倍，周长也会随之增加相同的倍数。

生：直径由8cm 变成2cm 缩小到它的1/4，周长也缩小到它的 1/4。

生：直径扩大到它的若干倍，周长也扩大到它的相同倍数。

师：同学们，你们分析一下第一列半径和第二列周长有什么联系呢？

生：当半径扩大到它的若干倍，周长也扩大到它的相同倍数。

师：为什么周长与直径（半径）会有这种变化规律呢？

生：周长与直径的比值不变，即一个因数不变时，另一个因数增加多少倍，周长（即积）也会随之增加相同的倍数。

教师在教学中应始终围绕“周长与直径的比值”进行分析、讨论，使学生能够明确该比值是一个固定值；教师通过多次擦除（或更改）数据，引导学生观察、比较、分析等一系列教学实践活动，则会逐步让学生感悟、理解“π”的本质特点。教师通过反复比较数据变化规律，既能够发挥出画龙点睛的作用，还能够突破本节教学难点——周长/直径是一个固定值。最终，提高学生对圆周率、周长计算公式的理解与应用能力。

四、艺术融合中欣赏“π”

无论是数学还是艺术都是一种创造性的活动并且包含了对于美的直接追求。教师应引导学生能够自主地将数学与艺术进行自主结合，以提高学生数学艺术审美能力。

这是一组将圆周率（π）转化成圆形彩虹艺术品的惊艳图集。在圆周率钢琴曲与图集中，原来看似枯燥乏味的数学，简单的一个圆周率，却可以和艺术完美地融合在一起。在优美的钢琴声中聆听这个无限不循环小数的韵律，在艳丽缤纷的图集中感受它的绝世之美。数学之美与艺术之美交织在一起，看似看不见、摸不到的圆周率，却以独特的形式展现出来，让学生越来越接近“π”。

总之，“π”既是人类智慧的结晶，又是数学学科中真、善、美的集合体，对此，教师应该抓住教学重点，突破教学难点，帮助学生认识到数学学科的魅力和数学世界的奥妙！