基于缺陷敏感度的加筋短板承载能力

刘存，赵冬强

1.航空工业第一飞机设计研究院 强度设计研究所，西安 710089 2.西北工业大学 航空学院，西安 710072

层流机翼设计技术可以使得机翼上表面维持较长的层流区域，从而降低飞机的阻力和使用成本，提高飞机性能。然而，层流技术对翼面结构制造、使用过程中存在的缺陷相当敏感。一旦翼面蒙皮具有初始缺陷，就引起层流的提前转捩，然而，对于实际翼面蒙皮结构，初始缺陷的存在是难以避免的。而几何缺陷对薄壳结构后屈曲承载特性的影响是该领域研究的重要方向[1]。一味追求结构减重和承载能力最大所获得的最优设计往往表现为对缺陷非常敏感，因此基于缺陷敏感度的承载能力评估具有重要意义[2]。几何缺陷影响结构的极限承载能力，具有几何缺陷的加筋板结构稳定性问题通常是结构大变形和材料弹塑性的双重非线性的复杂后屈曲问题，而非简单的分叉问题。

目前针对几何缺陷对加筋板稳定性及承载能力的影响问题国内外众多学者进行了相关理论和试验研究。Campbell等[3]通过扫描壁板表面实测几何缺陷，并通过ABAQUS命令*IMPERFECTION将缺陷引入有限元模型，分析了缺陷对蒙皮和筋条厚度均为0.9 mm的薄加筋板“坍塌”载荷的影响。Bernard等[4]研究了3种测量冷轧薄壁钢板几何缺陷方法，并评价了各自的优劣。Lanzi[5]实测了2块壁板的初始几何缺陷，并对测量数据进行了分析，得到了最大正负缺陷幅值以及幅值绝对值的平均值，通过参考真实位置改变蒙皮长桁节点位置来引入缺陷，同时比较了有无测量缺陷下2块壁板的试验和数值模拟的屈曲载荷及破坏载荷。Houston等[6]提出了采用整体次加筋板结构来考虑几何缺陷对壁板设计的影响。Paulo等[7]测量了不同形状和幅值的中长柱加筋板初始几何缺陷，并采用有限元模拟技术预测了具有测量缺陷的加筋板破坏载荷。Xu和Soares[8]使用ANSYS分析了实测缺陷与几何缺陷公式下窄加筋板的极限强度，结果与试验吻合高度一致，表明初始缺陷公式对分析极限强度是有效的。加筋板的几何缺陷形式和幅值未知的情况下，可以用屈曲特征模态来模拟其形态，用制造或者装配可以接受的缺陷上限来限定其幅值。刘存等[9]用有限元线性屈曲特性值分析获取特征模态，经过屈曲模态矢量归一化，乘以缺陷偏移量等计算处理后，用一阶屈曲模态代替局部初始缺陷，虽然此方法计算结构的后屈曲极限承载能力时计入初始缺陷的影响，但并不能保证与实际结构的缺陷一致，结果难免存在偏差。Hilburger等[10]基于实测几何缺陷数据标记典型制造缺陷，引入实测缺陷形状的有限元分析结果与试验屈曲载荷符合性良好。文献[11]指出考虑缺陷的非线性有限元分析可以得到高精度的屈曲和破坏强度，屈曲响应可影响制造的公差量。Rigo[12]和Couto[13]等研究了不同形状和幅值的缺陷对焊接薄壁结构极限强度的影响。

然而，国内外针对几何缺陷对加筋板的承载能力的研究仍有所欠缺，以上研究采用单个类型的缺陷公式或者特征模态，而均未对加筋短板的几何缺陷开展全面的研究和敏感度分析，且对加筋短板的失稳形态缺乏更精细的分析和认识，因此，对几何缺陷敏感度的深入研究就非常必要了。敏感度分析方法可以研究模型的输出变化对模型参数的敏感程度。筛选方法常用于筛除对模型输出影响较弱的输入，而用于敏感度分析的最初阶段。局部敏感度分析方法是指每次分析时只有被研究的输入变化，而其余输入固定不变的分析法，也称OAT(One-factor-at-A-Time) 方法[14]，其主要分析方法有：差分法、求导法、格林函数法等。全局灵敏度分析(Global Sensitivity Analysis,GSA)方法检验多个输入的同时变化对模型输出的影响，并分析每项输入以及各输入间的交互效应对模型输出的影响[15]，其主要方法有非参数方法[16-17]、基于方差的分析方法[18]、矩独立分析法[19]、基于失效概率的矩独立分析法[20-21]等。

本文采用原理简单、工程上便于使用的局部灵敏度分析法，结合工程经验，着重考虑灵敏度系数较大的变量，进行初弯曲、初偏心以及初变形对加筋短板承载能力的影响分析。给出了3种几何缺陷下加筋短板承载能力的设计许用值以及表征加筋短板初弯曲和初变形缺陷的计算公式，提出了通过加工制造要求的控制来降低几何缺陷对极限承载能力敏感度的设计建议，对指导加筋短板的结构强度设计具有重要的工程应用价值。

1 加筋短板承载能力分析

1.1 加筋短板模型

轴压载荷下加筋板后屈曲承载能力高精度的预测需要考虑初始几何缺陷、材料非线性、几何非线性以及高精度有限元模型。然而有限元模型的细节，如网格细化、理想化边界条件、分析方法同样需要事先进行研究。

选取的模型为长桁两侧各1/2长桁间距宽度的蒙皮的单加筋短板结构。根据研究方案，加筋短板的宽度150 mm，长度100 mm。横剖面如图1所示。材料为铝合金7150-T7751预拉伸厚板，性能参数[22]如下:压缩弹性模量Ec=73 723 MPa，泊松比μ=0.33，极限强度σb=565 MPa，压缩屈服强度σ0.2c=530 MPa。

图1 结构剖面简图Fig.1 Cross section of structure

具体剖面参数见表1。其中，t为长桁腹板厚度;t1和b0分别为长桁自由凸缘的厚度和宽度;t2和b1分别为长桁底边凸缘的厚度和宽度;h为长桁高度;R和R1为倒圆半径。

表1 剖面参数Table 1 Parameters of cross section

有限元模型建模时采用可以考虑大变形和材料非线性的壳单元。网格划分时，根据模型收敛性计算，为准确模拟结构因受压而产生的屈曲波，加筋之间蒙皮沿横向至少划分6个单元，加筋腹板沿高度方向至少划分3个单元，加强筋自由凸缘至少划分2个单元。为了保证建模与计算的准确性，单元数的设置尽可能使得各单元呈现正方形。

边界条件表征加筋板的实际受载情况，面内和面外边界条件都需考虑。选取能够代表机翼上翼面加筋板的典型结构为计算模型，在压缩载荷作用下，蒙皮自由边在与压缩载荷垂直的方向上的面内变形不受约束，长桁自由凸缘则可认为完全自由的。同时施加的边界条件应保证加筋板变形后相对两边相互平行。由于是整体加筋板，加筋对蒙皮的转动约束以及支撑作用通过共节点来实现。

有限元模型加载及约束如图2所示。蒙皮沿横向划分140个单元，长桁腹板沿高度划分60个单元，长桁自由凸缘沿横向划分20个单元，模型单元均为壳单元CQUAD4。

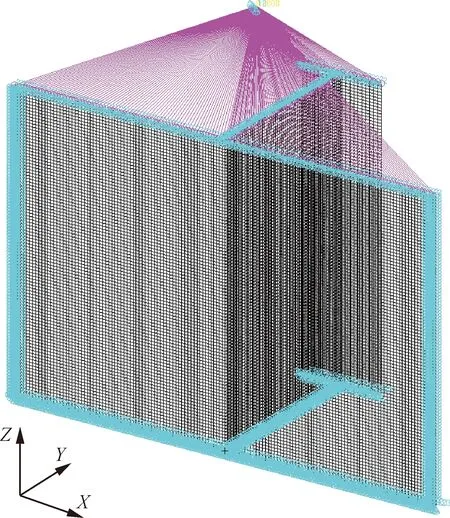
图2 有限元模型加载及约束图Fig.2 Loading and constrain condition of FEM

采用类型为RBE2的多点约束单元模拟试验机将载荷直接施加在加筋短板端面，加载点为主动节点，加载点约束XY方向的位移，加筋短板端面为从动节点，从动点约束蒙皮、长桁腹板、长桁凸缘各自的面外位移。约束端约束加筋短板端面三向XYZ位移。考核段约束蒙皮自由边面外Y向位移。有限元模型在加载点施加强迫位移载荷。

为了准确地预测加筋短板的承载能力，采用材料真实的本构关系。铝合金7150-T7751板材[14]应力-应变曲线如图3所示。

图3 7150-T7751板材应力-应变曲线Fig.3 Stress-strain curve of 7150-T7751 plate

1.2 求解策略

铝合金加筋板在航空领域飞机结构上使用已久，加筋板屈曲后刚度下降，在达到破坏载荷之前，加筋板进入后屈曲，之后发生连续的失效和坍塌。此领域的设计方法是基于Euler柱屈曲理论和Timoshenko板壳弹性稳定性理论，此类前期方法受边界简化和弹性假定等限制，适用范围有限，与试验相比，也不总能很好地预测临界载荷。而采用GMNIA(Geometrically and Material Nonlinear Analysis with Imperfections)分析方法则可高精度的预测，同时具备通用性。

求解加筋板的极限承载能力，可能需要跨越加载过程中载荷—位移曲线的屈曲分叉点，达到结构“坍塌”的极限载荷点，进而获得较为准确的结构的后屈曲承载能力，因此需要制定求解策略。通常情况下，非线性隐式分析可以较为准确地模拟加筋板结构的后屈曲行为，但当结构出现局部屈曲后，求解步长变小，求解时间激增，收敛性难以保证，需要设置合理的求解参数。Lanzi和Giavotto[23]则用动态显式分析求解复合材料加筋板的后屈曲特性。显式求解方法不存在收敛问题，但求解时间受模型复杂度、单元尺寸等参数影响较大。Abramovich等[24]用3种商用有限元求解器ABAQUS/Standard、ABAQUS/Explicit、NASTRAN模拟了带缺陷的加筋板后屈曲特性，并从计算时间、与试验数据吻合度等方面做了比较分析。

加筋板的几何缺陷在未知的情况下，可以用屈曲特征模态来替代。需要采用MSC.Nastran SOL105进行线性屈曲分析，获取有限元模型的屈曲模态。其次将一阶屈曲模态矢量归一化，乘以缺陷基矢量得到缺陷偏移矢量，采用SPCD模型数据卡施加强迫位移，将缺陷添加到有限元模型。最后基于Newton-Raphson迭代的弧长法(Arc-Length Method)SOL600隐式求解器进行非线性有限元计算。针对加筋短板的有限元模型，采用GMNIA分析方法进行求解。模型使用NLPARM卡定义非线性分析，载荷被分为87个等增量，采用ITER方法控制切线刚度修正，矩阵修正之前的迭代次数为40，每个载荷增量的总迭代限为1 000。采用NLPCI卡定义非线性静态分析中弧长增量求解策略，弧长法类型为MRIKS，最小弧长比为0.25，最大弧长比为4.0，期望收敛的迭代次数为40，每步最大迭代次数500。

1.3 结果分析

采用上述求解策略，对包含线性屈曲特征值法计算得到的屈曲模态转化为含初始缺陷的有限元模型进行求解，求解时开启大变形(LGDISP)考虑几何非线性，引入材料的弹塑性本构关系，进行非线性迭代分析计算，得到加筋短板的极限承载能力为368.3 kN。

表1中参数的加筋板试验件进行了5件，破坏载荷的试验与有限元结果比较见表2，同时给出了试验载荷平均值，表中序号对应试验件编号。PTEST为试验值，PFEA为有限元计算值，ε为有限元计算值相对于试验值的偏差：

表2 破坏载荷的试验与有限元结果比较Table 2 Comparison of failure load between test data and calculation results

ε=(PFEA-PTEST)/PTEST×100%

(1)

可见，采用有限元计算的加筋壁短板的破坏载荷与试验值误差均在10%以内，与试验值平均值误差为-0.46%。

提取载荷及位移的计算结果，绘制载荷-位移曲线如图4所示。

图4 加筋短板加载端载荷-位移曲线Fig.4 Load-displacement curve of loading end of stiffened short plate

由加筋短板加载端载荷-位移曲线可见，曲线在初始阶段呈线性，加载到368.3 kN时，曲线达到顶点，曲线斜率由正值变为负值，即为结构的极限载荷。随后位移继续增加，载荷下降，结构丧失承载能力。进一步分析加筋短板的破坏模式可见，长度方向1/2处蒙皮的面外变形最大且一侧蒙皮突起而另一侧蒙皮凹陷，两者组成一个完整的屈曲波；长桁腹板有明显的屈曲变形并向一侧弯曲。从整个破坏过程来看，长桁剖面发生局部失稳，压缩载荷继续增加，增加部分由较刚硬的角区承受，直到应力增加到足够的数值造成破坏。而从蒙皮和长桁腹板的失稳先后次序来看，蒙皮先失稳。有限元模拟失效时刻位移云图如图5所示，试验第1#件的失效形貌如图6所示。可见两者的失效模式一致。

图6 试验失效形貌Fig.6 Failure morphology of specimen

2 几何缺陷对加筋短板承载能力敏感度分析

2.1 几何缺陷的表征

轴压载荷下的无缺陷扰动的薄板，其屈曲特性只可能发生分叉型失稳(Snap-through)，而非此类结构设计要追求的极限承载能力(Collapse)，只有施加面外的初始缺陷扰动，才能将分叉失稳转化为与之接近的极限承载能力进行非线性数值计算。初始缺陷在加筋板的屈曲特性中扮演重要角色[25]，选择合适的初始缺陷，获得合理的极限承载结果。对于加筋板而言，初始几何缺陷可以分为整体几何缺陷和局部几何缺陷。具体而言，初始几何缺陷主要包括加筋板初始弯曲、载荷初始偏心和加筋板的初始变形。在有限元模型中，加筋板的整体几何缺陷往往以初弯曲的方式计入，通过将模型节点按照正弦波形式的偏移来实现。对于局部几何缺陷的施加，将柱型、板型和侧移型缺陷分别赋予蒙皮和长桁，同样通过施加强迫位移的方式来施加。

对于加筋板来说，在制造、安装、运输和服役过程中不可避免地产生某种几何缺陷，因此在进行有限元仿真分析时，引入几何缺陷是符合工程实际的。除了用线性屈曲特征值法计算得到的屈曲模态作为初始缺陷外，关于初始缺陷的规范[26-27]多来自国际船级社协会(IACS)和挪威船级社(DNV)，而对于专业的航空工程技术人员，航空加筋板结构引入何种模式、多大幅值的几何缺陷是值得花费时间和精力去深入研究的问题。为此，以加筋短板为例开展初弯曲、初偏心、初变形等缺陷对极限承载能力的敏感度分析。

2.2 初弯曲

基于欧洲钢结构协会(ECCS)委员会对通常情况下比较平直的铝合金挤压型材的初弯曲的测量结果，初弯曲总小于L/1 300，L为型材总长度，ECCS委员会在计算压杆的稳定性时采用了初弯曲为L/1 000的正弦扰曲线[28]。为研究初弯曲对加筋短板极限承载能力的影响，初弯曲采用正弦扰曲线式(2)，考虑加筋短板3种初弯曲方向，对扰曲线的幅值进行敏感度研究。

(2)

式中:wb为初弯曲扰曲线;a为加筋短板长度,mm;x为加筋短板沿长度方向坐标，mm。

根据图6所示的加筋短板试验件加工要求：零件A面(端面)与B面(端面)平行度0.05，长桁轴线面与A面、B面垂直度0.08。可计算参考扰曲线幅值分别为a/2 000、a/1 250。为考虑加筋短板初弯曲带来的影响，假设加筋短板初弯曲的幅值分别为a/1 000、a/1 250、a/2 000、a/2 500、a/3 000、a/3 500、a/4 000和a/4 500。在空间中的加筋短板弯曲方向有3种：弯向蒙皮正面、弯向蒙皮反面(即长桁凸缘方向)以及弯向腹板正面/反面。由于文中计算的加筋短板结构关于长桁腹板轴线对称，故弯向腹板的正面和反面计算结果相同。

各种幅值下，3种初始弯曲方向的载荷-位移曲线如图7所示。图中:skin-代表弯曲圆弧中心在蒙皮侧(即弯向蒙皮正面)，skin+代表弯曲圆弧中心在长桁侧(即弯向蒙皮反面)，web代表弯曲圆弧中心在腹板一侧(即弯向腹板正面/反面)。

图7 初弯曲加筋短板加载端载荷-位移曲线图Fig.7 Load-displacement curves of loading end for initial bending of stiffened short plate

由图7可见，加筋短板初弯曲的幅值为a/1 000、a/1 250、a/2 000、a/2 500、a/3 000、a/3 500、a/4 000和a/4 500，3种弯曲类型中skin-和skin+线性段斜率一致，web线性段斜率略高于skin-和skin+。说明在相同的初弯曲幅值和压缩位移下，加筋短板弯向蒙皮或弯向长桁自由凸缘方向时的应变小于弯向腹板方向的应变，在加筋短板设计中，更应关注弯向蒙皮或长桁自由凸缘方向的初弯曲，此方向也正是加筋板在机翼盒段中的主要受力方向。在机翼盒段的上翼面，加筋板受机翼翼型的制约，实际结构中初弯曲弯向长桁自由凸缘一侧。因此，研究skin+的承载能力具有直接的工程应用意义。

为了便于分析3种初弯曲幅值对加筋短板极限承载能力敏感度，将计算结果汇总见表3。其中，CDS(Curve Decrease Significantly)用于判断载荷—位移曲线是否出现拐点，即是否获得极限载荷，是代表有限元仿真结果得到了极限载荷，否代表未得到极限载荷。

由表3可见，skin+在加筋短板初弯曲的幅值为a/2 500时，极限承载能力达到最大值，为此，建议航空结构铝合金加筋板结构的初弯曲幅值取a/2 500。此时式(2)修正为式(3)：

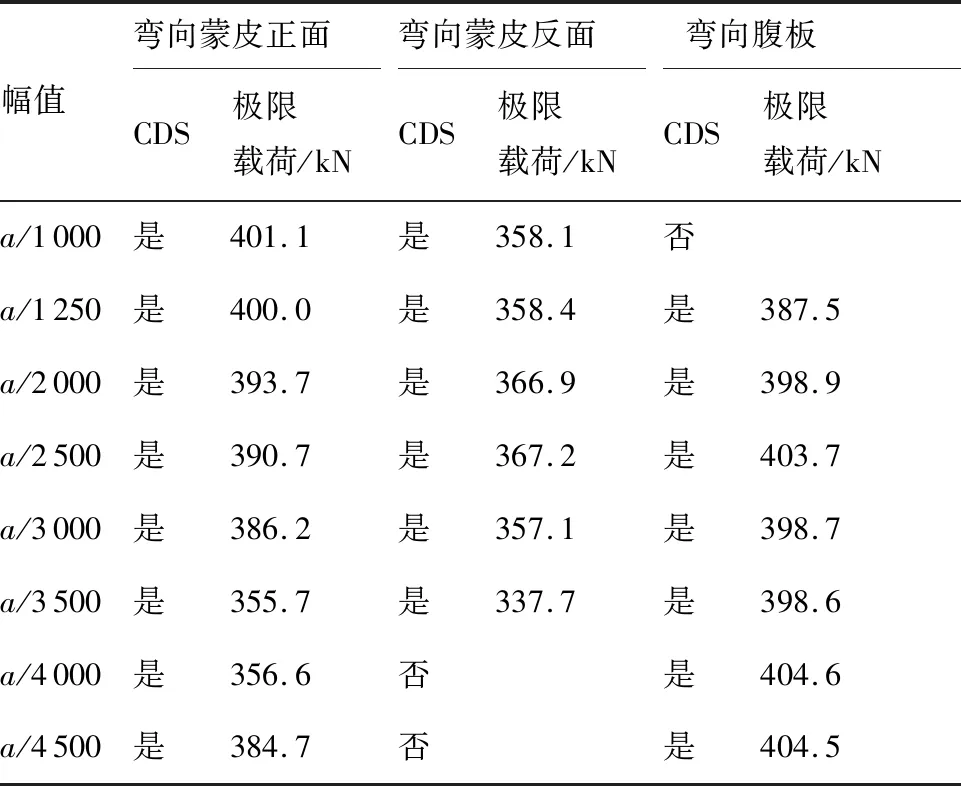
表3 初弯曲对极限承载能力的影响Table 3 Effect of initial bending on ultimate bearing capacity

(3)

此外，3种弯曲类型中skin+的极限载荷最小，在结构设计阶段，初弯曲弯向长桁自由凸缘方向的极限承载能力可用作加筋短板承载能力的设计许用值，而在结构件的服役使用中，应尽量避免。

2.3 初偏心

为研究加筋短板初始偏心对极限承载能力的影响，计算时引入了有限元模型的一阶屈曲特征模态形状。初偏心距取0.025倍、0.050倍、0.075倍、0.100倍、0.125倍的回转半径。初偏心的方向定义：向长桁自由凸缘侧偏心为正偏心，向蒙皮侧偏心为负偏心。形心、偏心后的位置及有限元计算的极限承载能力见表4。其中，回转半径为23.29 mm。

表4 初始偏心及极限承载能力计算结果Table 4 Calculation results of initial eccentricity and ultimate bearing capacity

由表4可见，各种匹配偏心距和偏心方向下，有限元仿真得到的极限承载能力均小于试验破坏载荷平均值370.0 kN，说明偏心是不利因素。在结构设计中应避免截面出现偏心，在强度计算中应计入结构真实的刚度特性，并考虑偏心带来的附加载荷。

正偏心加载端载荷-位移曲线如图8所示，负偏心加载端载荷-位移曲线如图9所示。可见，无论载荷施加正偏心还是负偏心，对加筋短板而言，线性段的斜率是一致的，极限承载能力相差不大，均在2%以内。加筋短板长细比小于20，处于短柱范围内，有限元模型通过RBE2将载荷施加在端面上，初始偏心值对极限承载能力的影响有限。

图8 正偏心加载端载荷-位移曲线Fig.8 Load-displacement curves for positive eccentric loading end

图9 负偏心加载端载荷-位移曲线Fig.9 Load-displacement curves for negative eccentric loading end

2.4 初变形

由于加工、制造等方面的原因，加筋板难以避免地带有一定的初始变形，而这种初始变形通常对压缩载荷作用下加筋板的大位移或后屈曲特性有明显的影响。加筋板的初始变形如图10所示。加筋板常见的初始变形缺陷包括柱型变形缺陷(图10(a))，板型变形缺陷(图10(b)和加强筋侧移型变形缺陷(图10(c))。

图10 加筋板初始变形Fig.10 Initial deformation diagram of stiffened panel

加筋短板的柱型变形缺陷、板型变形缺陷和加强筋侧移型变形缺陷的变形函数表达式分别为式(4)～式(6)。其中板型变形缺陷作用在加筋短板的蒙皮上，侧移型变形缺陷作用在加筋短板的加强筋上，柱型变形缺陷则是作用在加筋短板上，与初弯曲是相同的，2.2节已经进行了研究，并给出了推荐值。

板型变形缺陷：

(4)

柱型变形缺陷：

(5)

侧移型变形缺陷：

(6)

文献[18-19]给出了船体结构wp、ws的常用推荐值，而航空结构加筋板变形缺陷的幅值大小是值得深入研究的问题。为此，采用有限元方法计算了加筋短板的板型变形缺陷和加强筋侧移型变形缺陷在不同幅值下的极限承载能力，得到了各种变形缺陷下幅值对加筋短板极限承载能力的影响程度。不同幅值的板型变形缺陷下加筋短板极限承载能力如图11所示，不同幅值的侧移型变形缺陷下加筋短板极限承载能力如图12所示。

图11 板型变形缺陷下加筋短板载荷-位移曲线Fig.11 Load-displacement curves of thin-horse mode with initial imperfection of stiffened short plate

图12 侧移型变形缺陷下加筋短板载荷-位移曲线Fig.12 Load-displacement curves of side-ways with initial imperfection

由图11和图12可见，加筋短板初变形的wp、ws在不同的取值下，线性段斜率一致，而极限承载能力是不同的，说明初变形的wp、ws直接影响加筋短板的承载能力。因此，在加筋短板设计中，更应关注wp、ws的取值。图6中的加筋短板采用航空领域常用的制造加工公差量：蒙皮、筋条厚度公差为±0.15 mm，筋高公差±0.2，零件平面直线度每100 mm间隙不大于0.1 mm。经计算可得wp=4.28%、ws=5.82%。

为了分析板型变形缺陷和侧移型变形缺陷下幅值对加筋短板极限承载能力影响，将计算结果汇总见表5。

从表5中可知，加筋短板的板型变形缺陷的幅值wp为a/3 000～a/5 000时，极限承载能力相对稳定，且接近试验平均值。而侧移型变形缺陷ws的在a/4 000～a/10 000区域变化较小且接近试验平均值。为此，建议航空飞机铝合金加筋板结构板型变形缺陷幅值取a/5 000，侧移型变形缺陷取值为a/6 000。此时的式(4)修正为式(7)，式(6)修正为式(8)：

表5 初变形缺陷对极限承载能力的影响Table 5 Effect of initial deflection on ultimate bearing capacity

(7)

(8)

将试验件长度100 mm代入式(7)、式(8)可得幅值wp=2.0%、ws=1.67%。由此可见，要获得板型变形缺陷和侧移型变形缺陷下加筋短板的高承载能力，必须提高制造加工的精度：蒙皮厚度公差为±0.07 mm，零件平面直线度每100 mm间隙不大于0.028 mm。

3 结 论

通过加筋短板承载能力的分析和几何缺陷对加筋短板承载能力敏感度研究，得到以下结论：

1) 几何缺陷对加筋短板承载能力均有不同程度的影响，进行加筋短板极限承载能力分析时，应计入几何缺陷的影响。

2) 通过初弯曲对加筋短板承载能力敏感度分析，给出了航空结构铝合金加筋短板初弯曲的推荐公式，提出了结构设计许用值。

3) 通过初偏心对加筋短板承载能力敏感度分析，得到了在均匀受压载荷下，偏心距和偏心方向对加筋短板极限承载能力的影响有限的结论。

4) 通过初变形对加筋短板承载能力敏感度分析，给出了航空结构铝合金加筋短板的板型变形缺陷幅值以及侧移型变形缺陷的推荐公式，提出了通过控制加工制造公差量来提高结构承载能力的设计建议。