波浪前缘静子叶片对高速轴流风扇单音噪声的影响

同航，黎霖，卯鲁秦，向康深，乔渭阳

西北工业大学 动力与能源学院，西安 710129

轴流式压缩机(风扇、压缩机)作为现代高性能航空燃气涡轮喷气发动机的重要部件，是当代民用大涵道比涡扇发动机的主要噪声部件[1]，同时，随着商用航空发动机涵道比的增加，发动机效率得到切实提高，尾喷管出口速度显著减低，喷流噪声也随之减小，这使得风扇噪声的比重越来越大[2]，在愈加严苛的适航条件下，人们迫切需求新的航空发动机降噪手段[3]。

不仅在飞机发动机领域，叶轮机降噪也有很大需求。众所周知，大型风洞试验是飞行器研制环节中必不可缺的环节，它不仅在航空和航天工程研究和发展中起着重要基础作用，而且随着工业空气动力学的发展，在交通运输、房屋建筑、风能利用等领域更是不可或缺的。随着新一代高性能飞行器设计水平和空气动力学设计水平的不断提高，风洞试验精细化水平的不断提升，风洞试验要求变得愈加严苛，其中，风洞试验段内的噪声逐渐成为评价风洞综合性能的一个重要指标[4-5]。风洞试验段内过高的噪声对于风洞试验结果和试验设备有着诸多不利影响，例如：激起有害的抖振响应；缩短材料的疲劳寿命；造成结构破坏；延长精确采集信号所需要的平均时间等，特别是试验段高强噪声对非定常流试验、边界层转捩试验、激波/边界层干涉试验、湍流控制试验等的流动本质产生影响，直接影响着精细化流场试验的成败。因此，对风洞试验段噪声的有效控制，已经成为影响新一代高性能风洞发展和研制成败的关键因素，风洞的噪声水平也已经成为衡量新一代大型风洞技术水平的重要标志。

风扇噪声主要由两部分构成：单音噪声以及宽频噪声，其中：风扇单音噪声主要由风扇产生的黏性尾迹与后方静子叶片干涉而产生的周期性非定常载荷造成；风扇宽频噪声产生有多种方式，例如：转子尾迹湍流与静子间的相互作用、入口湍流与转子的相互作用、湍流边界层在叶片尾缘引起的自噪声等[6]。

噪声计算分析模型主要包括4类：半经验模型、解析模型、流场/声场混合计算模型以及全数值计算模型。流场/声场混合计算模型是目前发展最快的气动声学模型。这类模型首先通过CFD对声源部件周围非定常湍流流场进行计算，其次将声源流场参数耦合到基于气动声学理论的声远场计算中，从而实现流场/声场计算分析。利用混合模型对叶轮机械噪声进行计算分为：单音噪声混合预测模型和宽频噪声混合预测模型。相比于风扇单音噪声，宽频噪声的量级明显小了许多，同时，预测过程计算量大，准确度相对较低。因此，如何降低单音噪声仍然是低噪声叶轮设计的关键。

受猫头鹰翅膀前缘锯齿和座头鲸鳍前缘结节(呈波浪状前缘)的启发，许多国内外学者将其运用到孤立翼型并发现其在空气动力学特性和声学上有诸多好处[7-10]，许多研究表明，波浪前缘叶片可以改善失速后的动力特性，并延迟失速的发生，只略微降低一些失速前的动力特性[11-16]，与此同时可以显著降低湍流干涉宽频噪声[17-21]。

到目前为止，波浪前缘叶片降噪研究还是主要集中在孤立机翼研究方面，Reboul[22]和Tong[23]等研究了通过波浪前缘静子叶片来降低风扇噪声的措施。结果发现，使用波浪前缘静子叶片可以有效地降低风扇单音噪声和宽频噪声，但是其研究对象仍然与真实航空发动机和大型轴流压缩机高马赫数、高雷诺数的工况有一定差别。

为了将波浪形叶片构型融入真实发动机叶片设计中，进一步研究在真正三维风扇中波浪前缘静子叶片的声学优势及其降噪机制，为未来利用现代高水平优化设计算法[24-25]对航空发动机设计提供有效帮助，本文基于叶轮机械单音噪声混合预测模型(URANS/DBAA)对高转速、高雷诺数工况下真实三维风扇中波浪前缘静子叶片单音噪声的基本规律进行了分析研究。

1 计算方法

叶轮机单音噪声流场/声场混合模型以Goldstein管道内气动噪声基本方程[26]——声类比理论为基础，通过将叶轮机非定常流场数值模拟结果与Goldstein方程耦合，实现对叶轮机械单音噪声的模拟。单音噪声流场/声场混合模型计算流程图如图1所示。

图1 单音噪声混合模型计算流程Fig.1 Computational steps of tonal noise hybrid method

1.1 Goldstein管道声学基本方程

基于气动声学基本理论，在均匀流动条件下，运动介质中物体所产生的气动噪声主要由单极子噪声、偶极子噪声和四极子噪声组成[23]。对于真实压气机风扇来说，单极子噪声和四极子噪声可以忽略不计，主要噪声源是由叶片表面非定常载荷产生的偶极子声源，因此气动噪声声压公式可写为

(1)

式中：x和y分别代表观测点坐标和声源坐标；S表示运动物体表面；t为观察点接受时间；T为声源发射时间；下标“i”为离散后运动物体表面节点编号；G为管道格林函数；fi为运动物体表面处的非定常载荷；dS和dτ为面积微元和时间微元。

管道格林函数G可以写成如下形式：

(2)

Ψm(κmnr)=aJm(κmnr)+bYm(κmnr)

(3)

其中：Jm第1类贝塞尔函数；Ym为第2类贝塞尔函数；κmn为管道特征值；a、b为相应的比例系数。

在求解管道声压时，假设流体无黏,则叶片表面载荷f与叶片表面正交,于是有：f=Pn，其中P为叶片表面非定常载荷，n为叶片表面外法向量，进而式(1)可以写为

P(y,τ)dS(y)dτ

(4)

式中：SF为叶片表面积。

将式(4)利用傅里叶变换将时域信息转化为频域信息则有:

exp(imφ-iγmnx1)

(5)

式中：γmn为第(m,n)阶模态的轴向波数；Amn为频率ω下第(m,n)阶模态的声压振幅，其表达式为

P(y,ω-mΩ)}dS(y)

(6)

式中：Ω为叶片转速。

假设第s个叶片上所受的载荷为Ps(y,ω-mΩ)，则所有叶片对声压振幅Amn作出的贡献为

(7)

式中：V为静子叶片数。

于是可以得到不同模态下的声功率Wmn(ω)：

[Amn(ω)·(Amn(ω))*]

(8)

式中：ρ0为气体密度；U为气流速度；符号“-”表示上游方向,“+”代表下游方向；上标“*”代表复数共轭。

将频率ω下所有模态的声功率求和就可以得到总声功率:

(9)

对于单音噪声而言，噪声频率位于转子叶片通过频率及其高次谐波上，即

ω=jBΩRj=1,2,3,…

(10)

式中：B为转子叶片数；ΩR为转子叶片转速。

1.2 声源流场数值计算

由式(7)可知，要计算某个频率下的声压振幅Amn(ω)，就需要获得叶片表面对应频率下的非定常载荷力。对于单音噪声而言，噪声源是转子/静子干涉产生的周期性非定常气动载荷力。

通过URANS可以获得静子叶片表面周期性非定常载荷，图2所示为叶片通过频率(Blade Passing Frequency,BPF)及其高次谐频处叶片表面非定常载荷计算流程。对整个叶片不同位置处的周期性非定常压力进行叠加就可以得到整个叶片的周期性非定常载荷力。最后利用式(7)计算对应频率下模态为(m,n)的声压振幅，进而利用式(8)和式(9)就可以获得对应频率下的声功率。

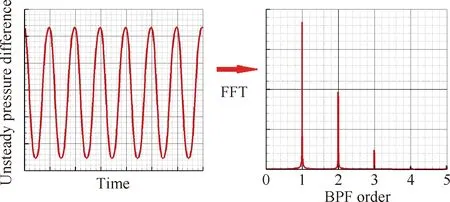
图2 叶片通过频率及其高次谐频处叶片表面非定常载荷计算流程Fig.2 Procedure of unsteady loading component on blade surface at BPF and its higher harmonics

2 流场/声场混合模型运用说明

为了说明URANS/DBAA混合模型可以用于研究高马赫数、高雷诺数工况下航空发动机单音噪声。首先，本文引用一个类似工况航空发动机的预测结果，以说明该方法的可靠性。其次，基于本文使用的URANS/DBAA混合模型对一台低速轴流风扇进行预测分析，以说明其精度。

2.1 高速轴流风扇预测结果

Tsuchiya等[27]利用混合模型与三维线性理论对叶片通过频率处单音噪声进行了预测。同时Tsuchiya将预测结果与试验对比后发现混合模型的精度明显更高。

表1给出了Tsuchiya等[27]研究的高速风扇设计参数。图3给出了该高速风扇噪声谱，其中纵坐标为声压级(SPL,Sound Pressure Level)。从图中可以看出，该风扇的基频约为7 500 Hz，并且1BPF处的单音噪声仍然处于最大水平。由于转子叶尖马赫数大于1，因而出现了超声速转子多重单音，总的来说叶片通过频率及其谐频处的单音噪声依旧明显。

图3 高速风扇噪声谱[27]Fig.3 Noise spectrum of high speed fan[27]

表1 高速风扇设计参数[27]Table 1 Design parameter of high speed fan[27]

图4给出了Tsuchiya等[27]分别利用三维线性理论和混合方法对高速风扇转/静干涉单音噪声的预测结果，图中PWL表示声功率级。与试验结果相比，混合方法的预测精度明显提高。

图4 声功率级对比结果[27]Fig.4 Comparison results of PWL[27]

2.2 低速轴流风扇预测结果

通过2.1节，可以说明混合模型可以用于预测高速轴流风扇中转/静干涉引起的单音噪声，本节将进一步说明本文所用URANS/DBAA混合模型的准确性。

Tong等[23]通过本文所用URANS/DBAA混合模型准确地预测了西北工业大学单级轴流风扇气动噪声试验台(NPU-fan)的转/静干涉单音噪声，并与试验结果做了对比。西北工业大学单级轴流风扇气动噪声试验台设计参数如表2所示。

表2 NPU-fan 设计参数Table 2 NPU-fan design parameters

如图5所示，Tong等[23]利用URANS/DBAA混合模型，得到了NPU-fan前3阶BPF下的声功率级水平。结果显示，1BPF和2BPF下的单音噪声预测误差小于1 dB，3BPF下的单音噪声预测误差约为2.1 dB。这表明，URANS/DBAA混合模型可以准确地预测风扇单音噪声。

图5 混合模型计算结果[23]Fig.5 Hybrid method calculation results[23]

同时，Tong等[23]以混合模型为基础，研究了多种波浪前缘静子叶片对降噪效果产生的影响。

综上所述，混合模型对转/静干涉单音噪声的预测在高速风扇和低速风扇中同样适用，本文所研究的高速风扇基频为2 800 Hz，处在NPU-fan基频950 Hz与Tsuchiya等[27]研究的高速风扇基频7 500 Hz之间，理论上预测误差应该处于这两者之间。同时，基于混合模型对波浪前缘静子叶片的降噪效果开展研究已有先例[23]，因此URANS/DBAA混合模型可以作为研究波浪前缘静子叶片低噪声设计的工具。

3 计算对象设置

本文选择了一台接近真实航空发动机的单级高速风扇(NPU-HiFan)作为研究对象，分析了波浪前缘静子叶片对其单音噪声产生的影响。表3给出了该风扇的主要设计参数。

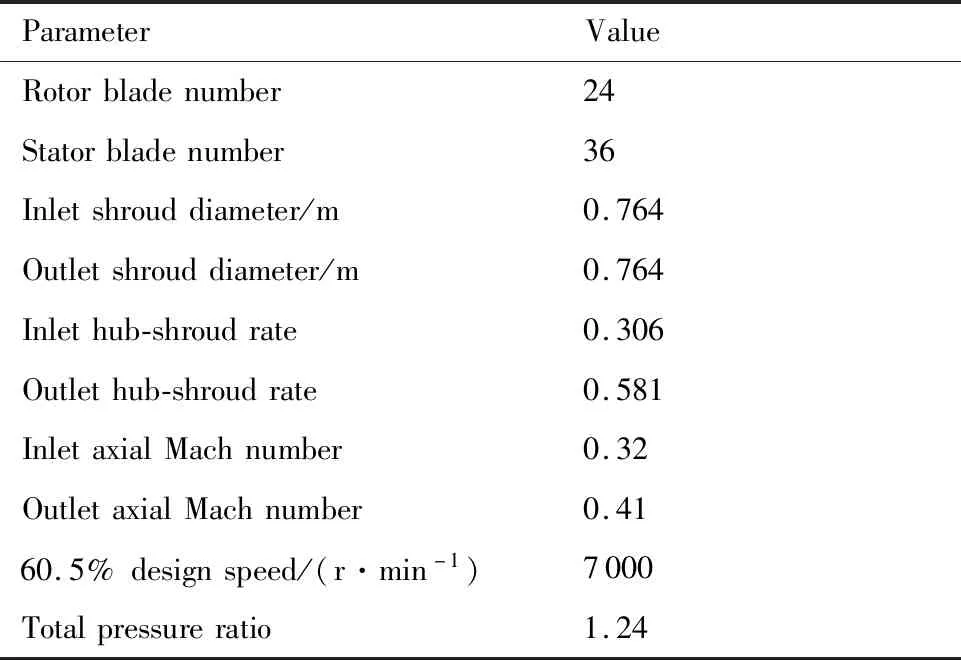
表3 NPU-HiFan设计参数Table 3 Design parameters of NPU-HiFan

3.1 波浪前缘叶片构型方法

图6为波浪前缘叶片构型示意图，可以看出，波浪前缘叶片主要由两个参数定义：波峰到波谷的幅值A，以及波浪前缘的周期W。

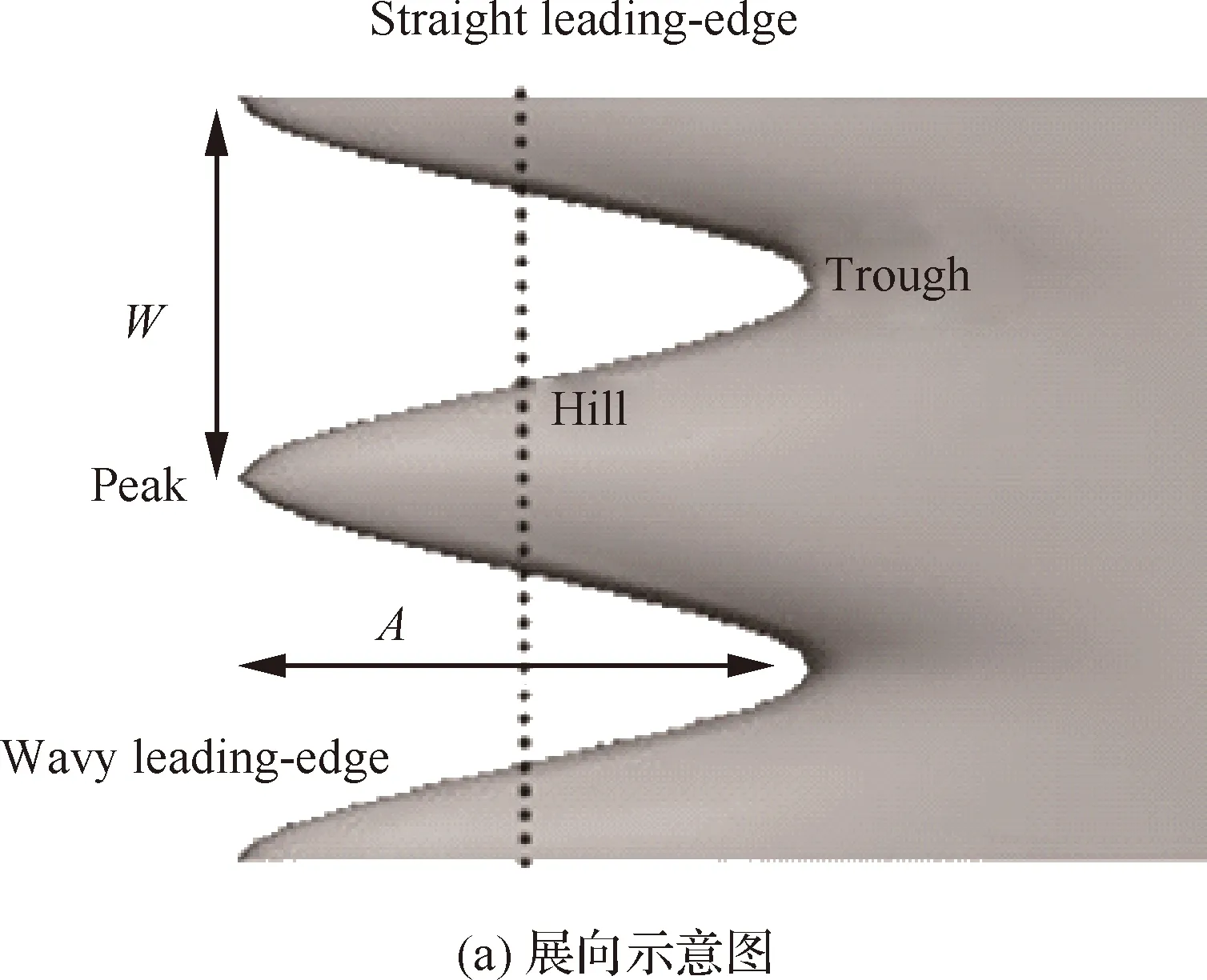
图6 波浪前缘叶片示意图Fig.6 Sketch of wavy leading-edge blade

对于波浪前缘叶片，其弦长沿径向方向r的分布为

(11)

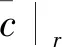
(12)

3.2 波浪前缘静子叶片结构

图7(a)为本文所研究的基准叶片构型，进一步地，根据3.1节对波浪前缘叶片构型的阐述，结合先前学者[22]的经验，设计出A9W15波浪前缘静子叶型，如图7(b)所示，其中：A9表示波浪前缘静子叶片幅值为9 mm，W15表示波浪前缘静子叶片波长为15 mm。

为了研究波峰与波长对单音噪声的影响，以A9W15叶型为参照，减小1倍波长设计出A9W7.5，增加0.5倍幅值设计出A13.5W15叶型，分别如图7(c)和图7(d)所示。

图7 基准叶片及波浪前缘静子叶片示意图Fig.7 Sketch of base stator blade and wavy leading-edge stator blade

3.3 计算设置

NPU-HiFan 风扇的转子和静子叶片数分别为24和36，可以用包含2个转子叶片和3个静子叶片的计算域来数值模拟，并准确地捕捉风扇级内部的流场信息，计算域示意图如图8所示。

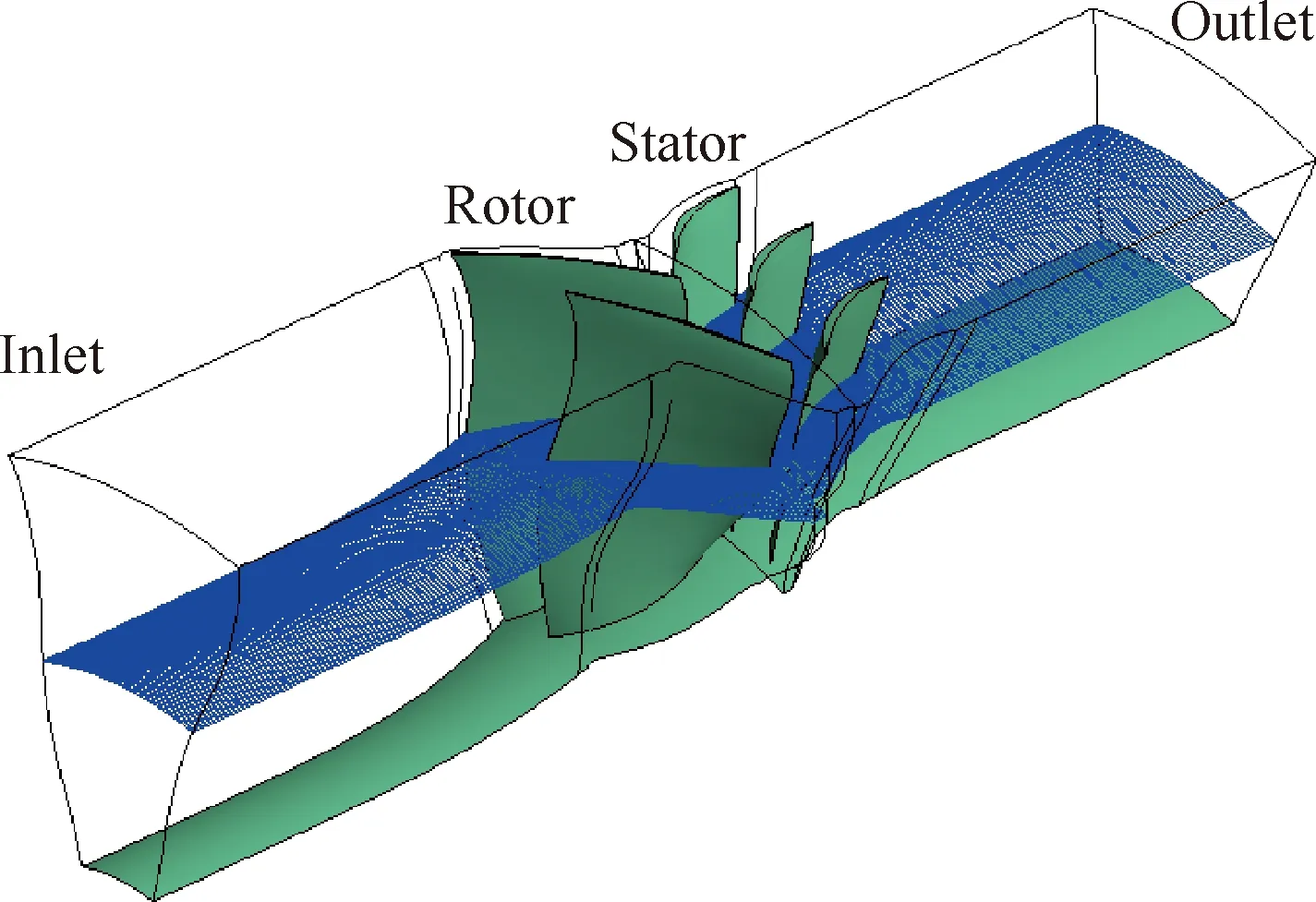
图8 计算域示意图Fig.8 Sketch of computational domain

在运用风扇单音噪声流场/声场混合预测模型过程中，静子叶片表面非定常压力脉动信息被用作声源信息以计算声场强度，准确地捕获静子叶片表面压力脉动信息对风扇单音噪声预测至关重要。因此，对于4种不同静子叶片前缘构型，都保证第1层网格的无量纲高度y+<1.2。最终确定网格数如表4所示。

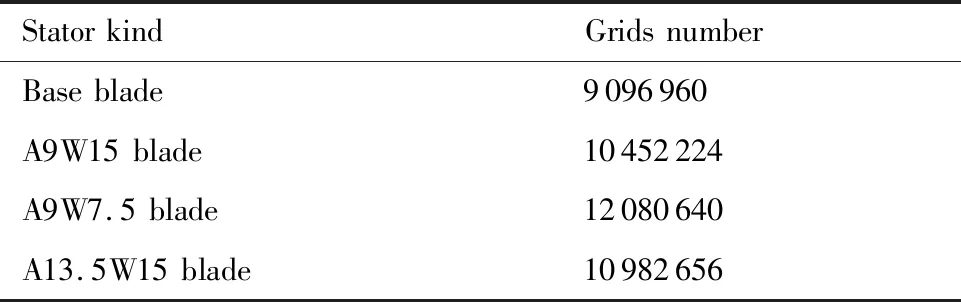
表4 计算域网格数Table 4 Grids number of computational domain

边界条件设置如下：进口为总压条件，出口为静压条件，转子/静子周向方向为旋转周期边界条件，壁面为绝热无滑移边界条件。时间步长为7.142 9 ×10-6s，即单个转子叶片通过周期对应50个时间步。URANS计算中采用SST(Shear Stress Transport)湍流模型。

4 计算结果

4.1 管道声模态

对于NPU-HiFan风扇而言，转子转速为7 000 r/min，对应1BPF为2 800 Hz，2BPF为5 600 Hz，3BPF为8 400 Hz。叶轮机械主要关注前3阶BPF对应的单音噪声，图9给出了20～10 000 Hz 区间，风扇进口噪声“截通”的最大周向模态数和最大径向模态数。

图9 最大截通模态数Fig.9 Max cut-on mode number

在计算状态下，不同频率的单音噪声对应的截通模态数如表5所示，其中，h为谐波次数，k=0,1,2…。从表中可以看出，对于 1BPF 而言，m=-12是离散单音的主要周向模态，其中包括n=0和n=1两个径向模态；在2BPF 和3BPF下，由于频率的提高，使得处于“截通”状态的模态数也随之增加。

表5 管道声模态分析(B=24,V=36)Table 5 Duct sound mode analysis(B=24,V=36)

4.2 气动性能

表6为基准叶片与3种波浪前缘静子叶片总增压比、等熵效率的计算结果对比。相较于基准叶片，A9W15叶型在总压比方面降低最多，约为0.8%；A9W7.5叶型在总压比方面降低最少，约为0.1%；A9W15叶型在等熵效率方面降低最多，约为0.3%；A13.5W15叶型在等熵效率方面降低最少，约为0.1%。由此可见波浪前缘静子叶片对等熵效率和总压比的影响并不大，尤其是对于大型风洞压缩机，这一点损失就显得微不足道了。

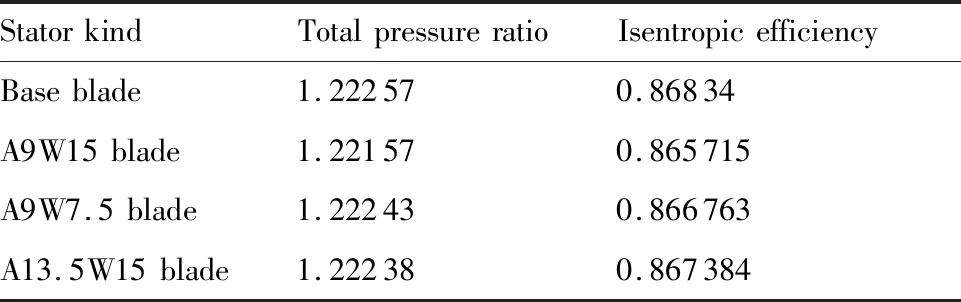
表6 气动特性Table 6 Aerodynamic performance

4.3 流场结果

由于3种波浪前缘静子叶片对流场的影响类似，这里采用基准叶型和A9W15叶型对比分析波浪前缘静子叶片对流场产生的影响,研究对象静子来流平均马赫数约为0.49，基于静子叶片弦长的雷诺数约为1 040 000,与NPU-fan相比增加了大约3倍，更接近真实航空发动机压气机部件和大型风洞压缩机的工况。

图10、图11为叶片表面极限流线分布，对比吸力面极限流线与压力面极限流线，对于NPU-HiFan风扇，波浪前缘静子叶片主要改变的是压力面的流场。对于基准叶片，50%～80%叶高处，叶片前缘会产生回流涡旋，气流由叶片压力面流向叶片吸力面。对于波浪前缘叶片，在前缘部分流体存在较强的展向流动，将50%～80%叶高处的回流涡旋打破。

图10 压力面极限流线Fig.10 Pressure surface limit streamline

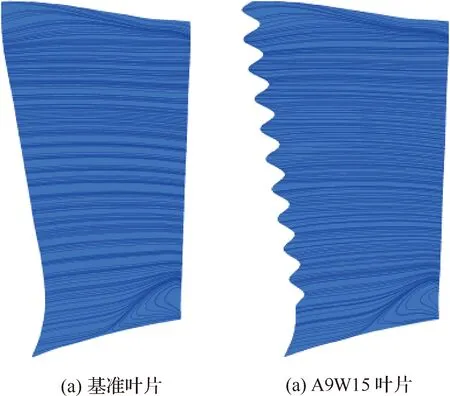
图11 吸力面极限流线Fig.11 Suction surface limit streamline

图12为郭鑫[28]关于波浪前缘附近复杂的三维涡系结构的解释，对于本次计算有很好的参考价值。图12显示，波浪前缘波谷位置能够观察到较弱的旋涡流线结构，其中位置1与位置2处涡的旋向为逆时针，位置3处涡的旋向为顺时针，一个波浪结构能够引起一对旋向相反的涡对。随着涡的发展，涡的强度不断增强，位置1处的涡逐渐向下游发展形成位置4所示的较为明显的逆时针旋转的流向涡结构。位置2处的涡向负展向移动，在位置5处转向正展向方向移动，并与位置3处涡混合，向下游继续发展，然而由于在中部存在较强的开式分离，同时受到较强的流向逆压梯度的影响，使得该涡结构受到挤压转向垂直于吸力面方向卷起，形成位置6所示的顺时针旋转的横向涡结构。

图12 波浪前缘位置涡结构示意图[28]Fig.12 Sketch of vortex structure at wavy leading-edge[28]

由于对于NPU-HiFan风扇，波浪前缘静子叶片主要影响压力面的流场，接下来的分析主要围绕静子压力面进行。图13自上而下为沿着弦向的基准叶片和波浪前缘静子叶片压力面流向涡量发展云图，对比图10(a)与图13(a)，可以看出，对于基准叶片，除去50%～80%叶高处，基准叶片基本不存在明显的流向涡结构，沿着弦长方向边界层会逐渐增厚并转捩为湍流边界层。从图13(b)可以看出，波浪前缘静子叶片会诱导产生一对反向旋转的对涡结构，并向下游发展。对比图13(a)和图13(b)，波浪前缘叶片可以将基准叶片70%展向高度处的大尺度涡旋打碎。

图13 叶片压力面流向涡量分布Fig.13 Streamwise vorticity distribution on pressure surface of blade

4.4 声学结果

表7和图14给出了基准静子叶片与3种波浪前缘静子叶片的前传风扇单音噪声声功率级。对比基准静子叶片和波浪前缘静子叶片，可以发现波浪前缘静子叶片可以有效降低NPU-HiFan前3阶BPF下的单音噪声。

图14 单音噪声声功率对比Fig.14 Comparison of PWL of tonal noise

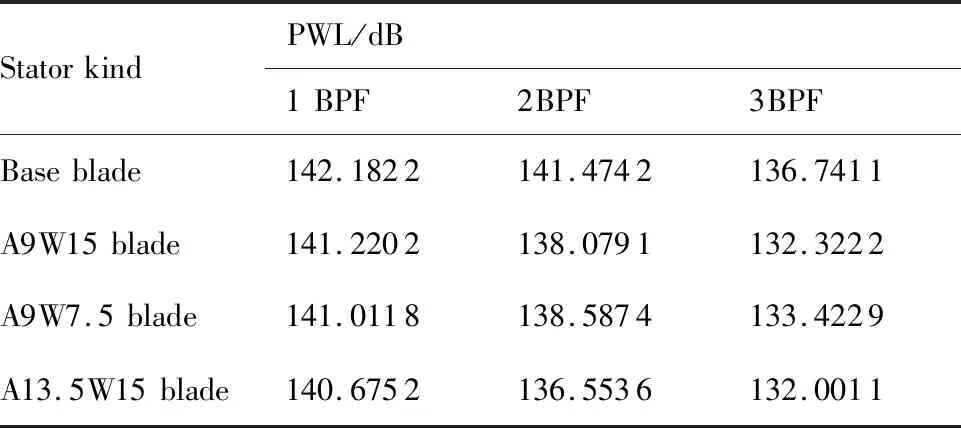
表7 NPU-HiFan 单音噪声声功率级Table 7 Tonal noise PWL of NPU-HiFan

1) 对比基准叶型和A9W15叶型，其中1BPF 单音噪声声功率降低0.962 dB，2BPF 单音噪声声功率降低3.395 1 dB，3BPF 单音噪声声功率降低4.418 9 dB。

2) 对比A9W15叶型和A9W7.5叶型，其中 1BPF单音噪声声功率降低0.208 4 dB，2BPF和3BPF 单音噪声声功率反而有所提升，可能的原因在4.5节中进行分析。

3) 对比A9W15叶型和A13.5W15叶型，其中 1BPF单音噪声声功率降低0.545 dB，2BPF单音噪声声功率降低1.525 5 dB，3BPF单音噪声声功率降低0.321 1 dB。

4.5 降噪机理

由于风扇噪声主要是由静子表面叶片非定常压力脉动产生的，但是只考虑由时域流场作傅里叶转化后得到的频域下叶片表面压力脉动显然没有考虑到噪声在管道内的传播效应。因此，为了能够深入分析波浪前缘静子叶片对前传噪声的影响机制，在分析波浪前缘静子叶片对前传噪声影响时，将使用包括管道特征函数和静子叶片法向量影响的压力脉动无量纲项PNormal代替Ps(y,ω-mΩ) 来表示静子叶片表面的声源信息，结合式(5) 可以得到PNormal表达式为

(13)

式中：P0为标准大气压。

图15～图20分别给出了风扇进口1BPF、2BPF和3BPF单音噪声对应的静子叶片表面PNormal分布云图，其中“abs(PNormal)”表示其幅值，“Re(PNormal)”表示取其实部。

从图15可以看出，对于1BPF，波浪前缘静子叶片对abs(PNormal)分布产生的主要影响在压力面，这与波浪前缘静子叶片对流场产生的影响类似；对于吸力面：主要使得位于40%叶高和叶片顶部的声源强度在一定程度上降低；对于压力面：使得基准叶片20%弦向位置处的声源得到有效抑制，同时减小了声源面积。从图16可以看出，对于1BPF，波浪前缘静子叶片对Re(PNormal) 分布产生的影响十分明显，由于1BPF对应的频率为2 800 HZ，此时截通的最大径向模态数为5，而波长为15 mm的波浪前缘静子叶片有10个周期的正弦波形，波浪前缘静子叶片的引入，使得相位变化加剧，有效降低了1BPF单音噪声。

图15 1BPF 静子叶片表面声源分布(abs(PNormal))Fig.15 Noise source distribution on stator blade surface at 1BPF(abs(PNormal))

图16 1BPF 静子叶片表面声源分布(Re(PNormal))Fig.16 Noise source distribution on stator blade surface at 1BPF(Re(PNormal))

从图17可以看出，对于2BPF，波浪前缘静子叶片对abs(PNormal)分布产生的影响在压力面和吸力面都很明显，对于吸力面：有效降低了80%叶高处的声源，其中A13.5W15叶型的效果最为明显；对于压力面：波浪前缘叶片有效抑制了前缘声源强度，相比之下A9W15叶型的抑制效果要好于A9W7.5叶型。如图18所示，对2BPF对应的频率5 600 Hz而言，此时截通的最大径向模态数为9，因此相对于1BPF，2BPF下波浪前缘静子叶片的引入对相位产生的影响效果就不那么明显了，对比表7中2BPF下各种叶型的声功率，便解释了2BPF下A9W15叶型降噪效果要优于A9W7.5叶型的原因。

对比图19和图17，对于3BPF，波浪前缘静子产生的影响与2BPF类似。如图20所示，3BPF下频率为8 400 Hz，此时截通的最大径向模态数为13，相位产生的影响更为薄弱，这也是表7中3BPF相对与2BPF结果A9W7.5降噪效果更弱的原因。

图17 2BPF 静子叶片表面声源分布(abs(PNormal))Fig.17 Noise source distribution on stator blade surface at 2BPF(abs(PNormal))

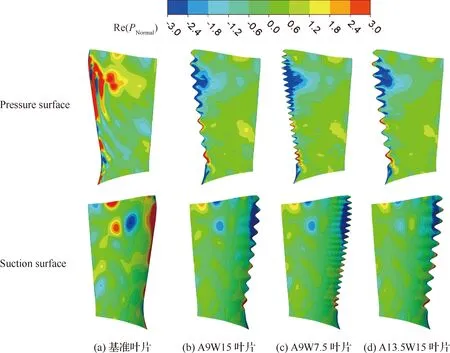
图18 2BPF 静子叶片表面声源分布(Re(PNormal))Fig.18 Noise source distribution on stator blade surface at 2BPF(Re(PNormal))

图19 3BPF 静子叶片表面声源分布(abs(PNormal))Fig.19 Noise source distribution on stator blade surface at 3BPF(abs(PNormal))

图20 3BPF 静子叶片表面声源分布(Re(PNormal))Fig.20 Noise source distribution on stator blade surface at 3BPF(Re(PNormal))

5 结 论

1) 本文分别采用3种不同的波浪前缘静子叶片与基准静子叶片对比，对高速轴流风扇进行了气动和声学性能评估。结果表明，3种不同的波浪前缘静子叶片能够将前3阶BPF风扇单音噪声声功率级有效降低，此外，波浪型前缘对风扇的气动性能影响不大。

2) 除了确定了波浪前缘静子叶片的降噪效果外，还研究和分析了这种降噪的机理。波浪前缘静子叶片可以将大尺度涡旋打碎成为小尺度涡旋，并诱导出许多流向涡结构，可以显著地改变叶片前缘压力脉动的分布。

3) 与文献[23]中的低速轴流风扇相比，波浪前缘静子叶片对于高马赫数、高雷诺数工况的高速轴流风扇降噪显得较为困难，但是仍有不错的降噪效果。

4) 波浪前缘静子叶片是通过改变叶片表面压力脉动振幅和相位关系来减小噪声强度的，研究发现增加波浪前缘静子叶片幅值可以有效降低声源面积和强度，而单纯改变波长不一定对降噪有利，所以在设计波浪前缘静子叶片时应将相应频率下截通的最大径向模态数考虑在内。