蜂群无人机充电排队优化方法

王云哲，徐国宁,*，王生，李兆杰，蔡榕

1.中国科学院 空天信息创新研究院，北京 100094 2.中国科学院大学，北京 100049

近年来，蜂群无人机由于可以体现出蜂群的整体优势，完成较复杂的任务，相比单一无人机，蜂群可以对多无人机执行任务带来很多的优势，成为国内外研究的热点[1-3]。但是由于电源技术的水平和限制，现有无人机续航时间短，需要经常充电，因此蜂群无人机快速充电以及充电排队问题成为制约其快速发展和大面积应用的瓶颈技术，特别是充电排队问题影响着蜂群无人机执行任务的效率和效果。据现有文献查询，蜂群无人机充电排队的研究未曾报道，本文基于排队理论对蜂群无人机充电排队技术进行研究。

在常规的电动汽车排队充电研究中，文献[4]基于排队理论建立了充电设施系统排队模型，通过合理配置充电设施，提高了电网负荷率。文献[5] 基于排队理论对电动汽车充电站的24小时充电负荷曲线进行建模，使用随机最优潮流和模型预测控制方法研究了不确定性的影响。文献[6]基于排队理论中的M/M/s模型和流体方程，计算了高速公路充电站的电动汽车到达率。文献[7]针对电动出租汽车充电站排队系统，对M/G/k排队模型和M/M/k排队模型进行了对比，分析了电动汽车到站的荷电状态对排队系统的影响，并提出了提高系统服务能力的措施。文献[8]利用排队理论在服务系统优化设计方面的优势，构建了电动汽车充电桩的最优台数设计模型，同时利用排队理论分析了充电站的服务水平和运行效率。文献[9]采用基于排队论的充电机配置方法，提出了布局最优化的数学模型，并基于M/M/s模型，以平均等待时间为标准确定充电站的规模。文献[10]利用电动汽车充电站排队论模型，研究了基于路径需求和基于点需求下的充电站选址定容问题。文献[11]基于排队理论进行了充电站的容量优化配置。

在面向蜂群无人机充电时，由于其工作环境的特殊性，可能需要悬停等待充电，比常规充电工况多，因此需要加入系统容量的限制。即，当某一充电平台可容纳的无人机数量达到限定值后，无人机将不再前往这一平台，从而避免了无人机在悬停等待的队列中将电量耗尽。

目前充电方法包括集中式充电和分布式充电2种，其中集中式充电(Concentrated Charging，文中用下标“c”表示)将充电平台集中在一处，对蜂群无人机进行充电。而分布式充电(Distributed Charging，文中用下标“d”表示)将充电平台分散放置。本文基于M/M/1/m[12]模型和M/M/n/m[13-16]模型对多充电平台的2种排布方式展开研究。

1 排队系统基本理论

在排队论中，通常采用6个特性，实现对一个排队系统的分析[17]。它们的描述通常依据Kendall提出的方法[18]：

A/B/N/S/C/Z

式中：A为输入过程；B为服务时间；N为服务员数量；S为系统容量；C为客源数量；Z为排队规则[17-19]。

当系统容量为固定值，且排队规则为先到先服务时。依据Kendall提出的方法，该类排队模型可表示为

A/B/N/S

第2节中，将着重对M/M/1/m和M/M/n/m2种排队模型进行分析。其中M表示顾客之间的到达时间间隔和服务员为顾客提供服务的时间服从指数分布[19]；m代表排队系统中的系统容量;n代表排队系统中的服务员数量

2 2种排队模型

2.1 M/M/1/m模型

M/M/1/m模型的状态转移图如图1所示，图中：λ和μ为上述指数分布对应的参数。

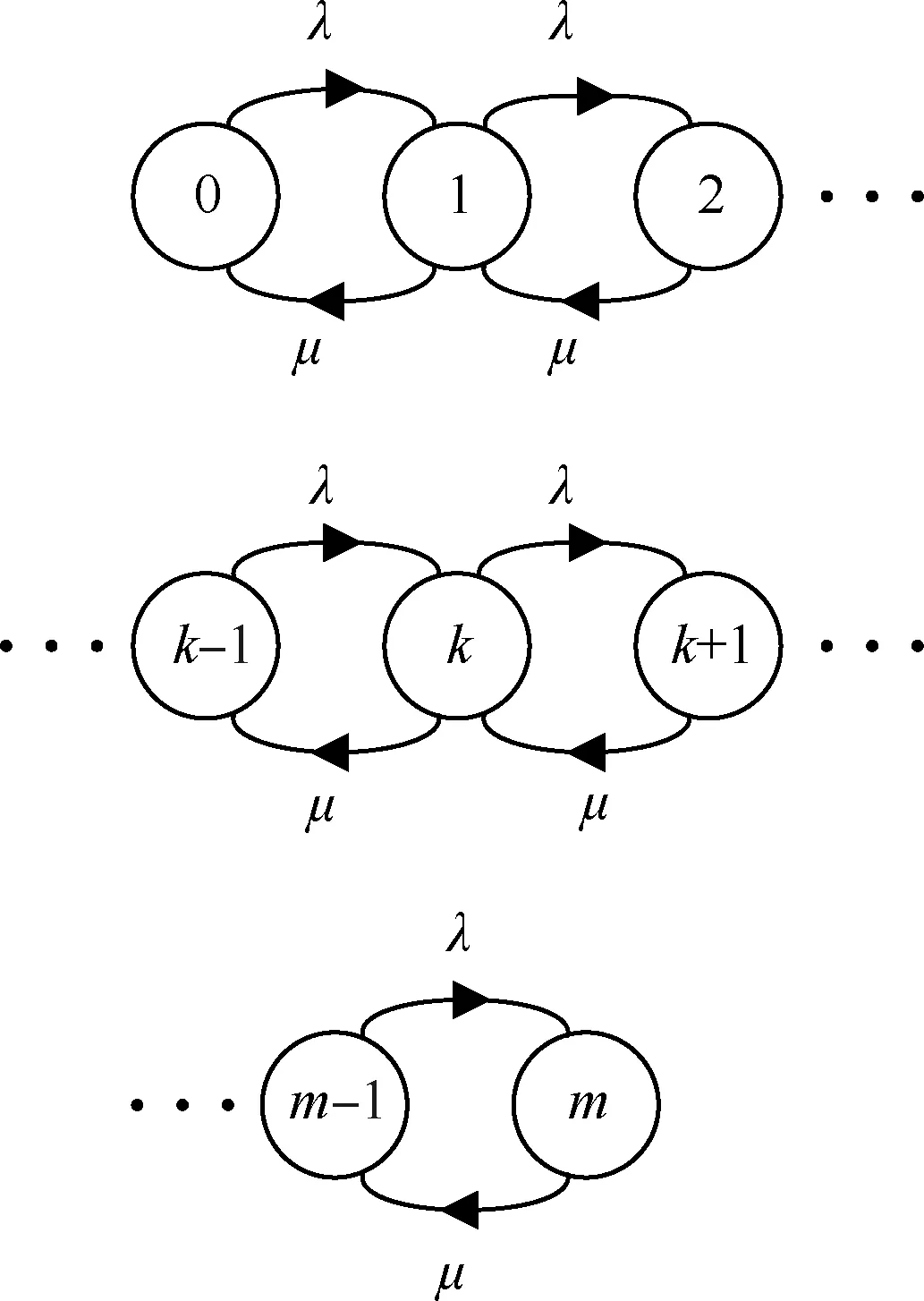
图1 M/M/1/m模型状态转移图Fig.1 State transition diagram of M/M/1/m model

由图1可以列出平衡方程为

(1)

式中：Pk为系统中有k位顾客时的概率。定义M/M/1/m模型中系统的服务强度为

(2)

经过推导，可以得到M/M/1/m模型，队列中顾客的平均数量为

(3)

因此，借助Little定理[20-21]，可以求得顾客在队列中等待的时间为

(4)

2.2 M/M/n/m模型

M/M/n/m模型也可采用如图2所示的状态转移图求解概率分布。

图2 M/M/n/m模型状态转移图Fig.2 State transition diagram of M/M/n/m model

由图2可列出平衡方程为

(5)

定义M/M/n/m模型中系统的服务强度为

(6)

通过推导，可得到M/M/n/m模型中的平均队列长度为

(7)

基于Little定理，可以计算出M/M/n/m模型中，顾客在队列中等待的时间为

(8)

3 2种排队充电方式解析

3.1 分布式充电方式

面向蜂群无人机的分布式充电的示意图如图3所示。

图3 分布式充电示意图Fig.3 Schematic diagram of distributed charging

图4 分布式充电等效图Fig.4 Equivalent diagram of distributed charging

(10)

基于2.1节对M/M/1/m的分析，以及式(10)，可以计算出分布式充电的平均队列长度Ld和平均等待时间Td分别为

(11)

Td=

(12)

3.2 集中式充电方式

针对蜂群无人机的集中式充电的示意图如图5 所示，n个充电平台集中放置在一起。无人机到达后，在单一共享的队列中等待充电。依据3.1节 所述，M/M/1/m模型可用于描述其中一个充电平台。因此，在集中式充电的背景下，n个充电平台可等效为M/M/n/nm模型。

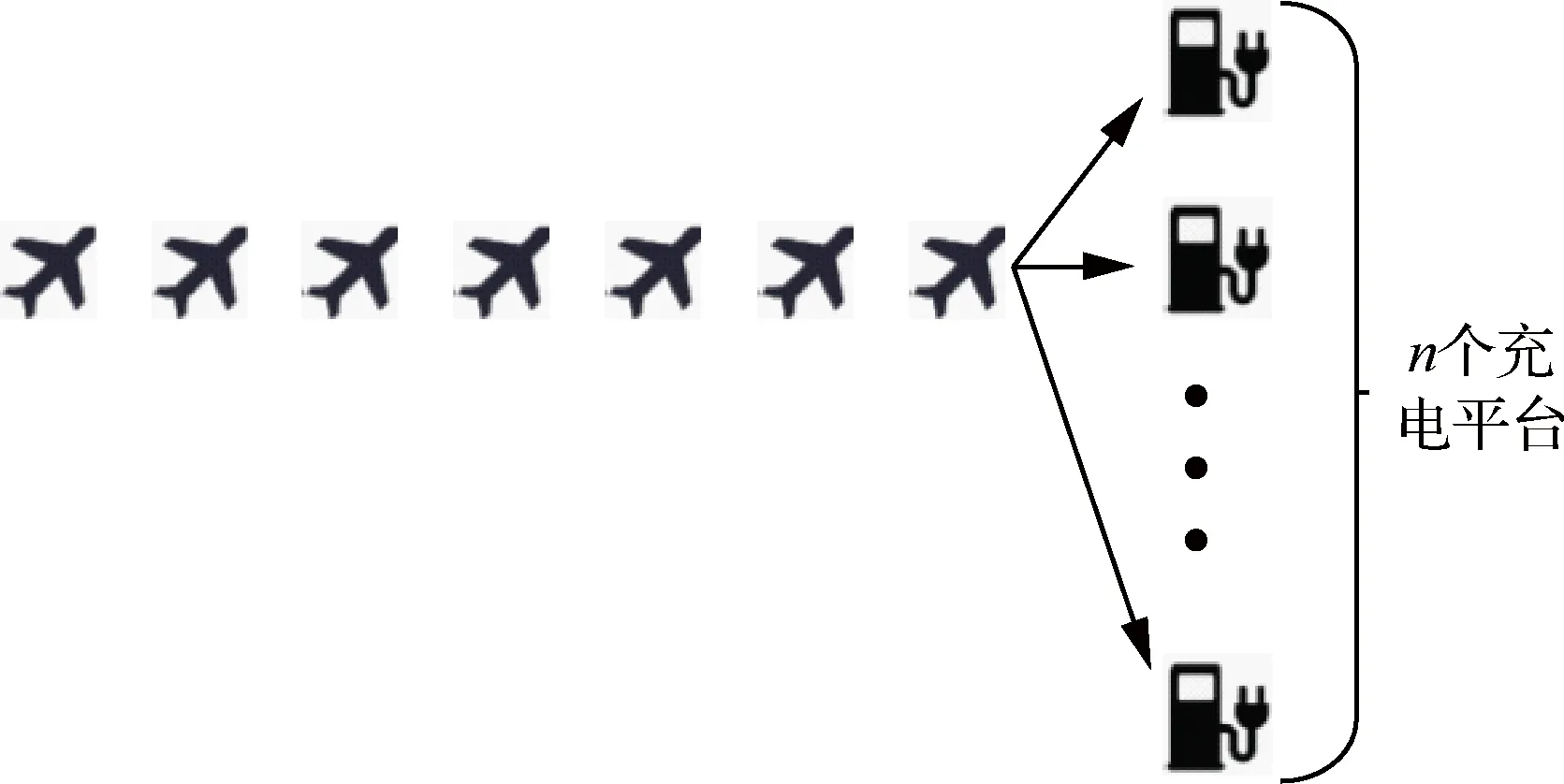
图5 集中式充电示意图Fig.5 Schematic diagram of concentrated charging

基于本文2.2节对M/M/n/m模型的分析，经计算可得到，集中式充电的平均队列长度Lc和平均等待时间Tc分别为

(13)

Tc=

(14)

(15)

(16)

4 数值计算及结果分析

基于第3节的公式推导以及对分布式充电的等效，如式(17)所示，2种排队充电方式的服务强度相等。而针对蜂群无人机，服务强度即为：“单位时间返回充电平台的无人机数量与单位时间离开充电平台的无人机数量的比值”。在下文中，将使用无量纲量ρ来表述这一相等的服务强度。

(17)

本文基于MATLAB软件，对2种排队方式的平均队列长度和平均等待时间进行计算。具体的参数设置如表1所示。

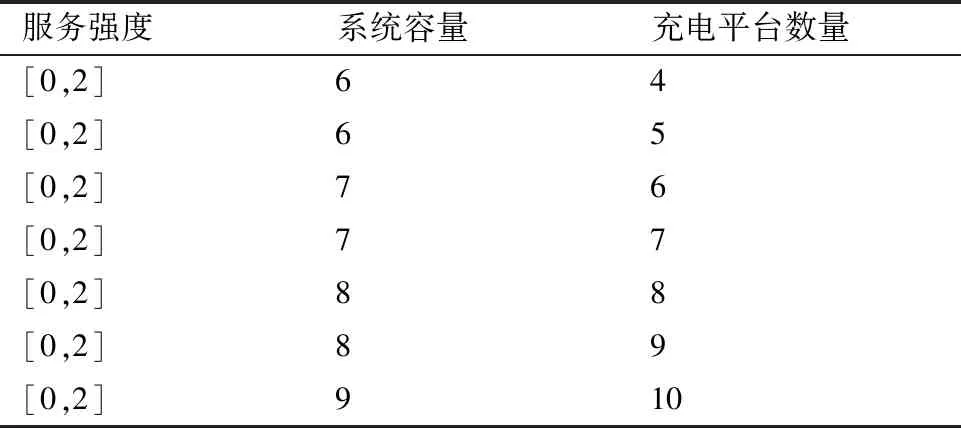
表1 参数设置Table 1 Parameter setting

4.1 平均队列长度

当系统容量设定为6时，随着服务强度和充电平台数量的变化，2种充电方式的平均队列长度对比如图6所示。

依据图6可以看出，在服务强度的区间为[0,2]时，若以平均队列长度作为评价充电方式优劣的指标。随着服务强度的增加，两者的队列长度均随之增长，但存在一个分界点。即分布式充电的队列长度曲线会与集中式充电的队列长度曲线产生交叉点，在交叉点前，服务强度较小时，分布式充电的队列长度高于集中式充电的队列长度。在这一交叉点后，分布式充电的队列长度低于集中式充电的队列长度。下面，将系统容量依次设置为7、8和9时，继续对比2种充电方式的平均队列长度。

图6 系统容量为6时的平均队列长度对比Fig.6 Comparison of average queuing length when system capacity is 6

从图7～图9中可以看到，随着服务强度的增加，将会观察到与系统容量为6时一样的现象。通过数值分析中的二分法，取区间为(0.7,0.9)，精度为0.000 1，可以求解出每一个交叉点的横坐标，如表2所示。综合上述曲线，可以观察到，服务强度较低时，在以平均队列长度作为评判指标时，集中式充电比较有优势，但随着服务强度的增加，分布式充电的优势逐渐体现。

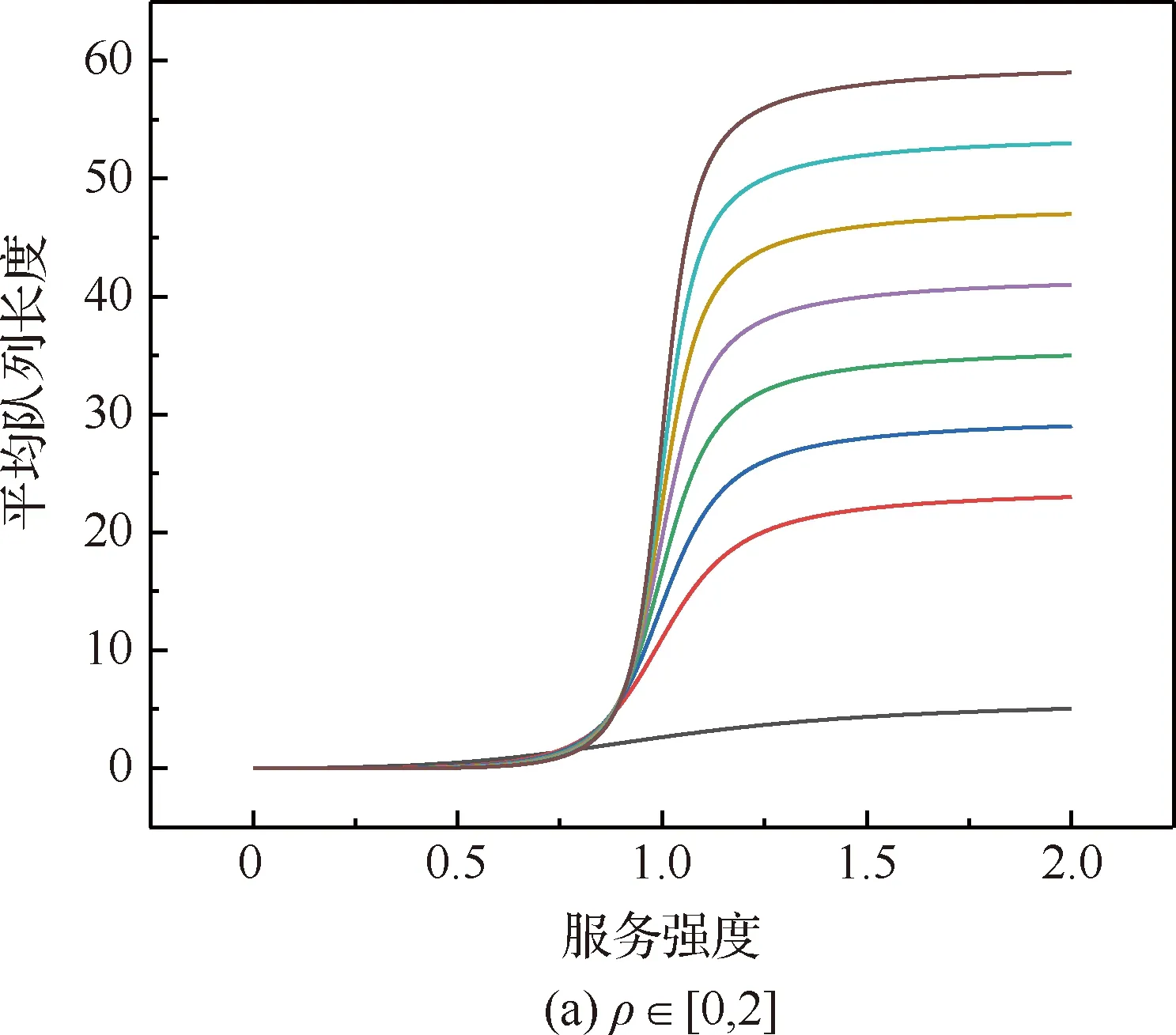
图7 系统容量为7时的平均队列长度对比Fig.7 Comparison of average queuing length when system capacity is 7

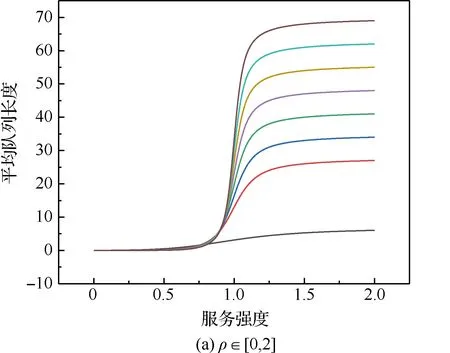
图8 系统容量为8时的平均队列长度对比Fig.8 Comparison of average queuing length when system capacity is 8

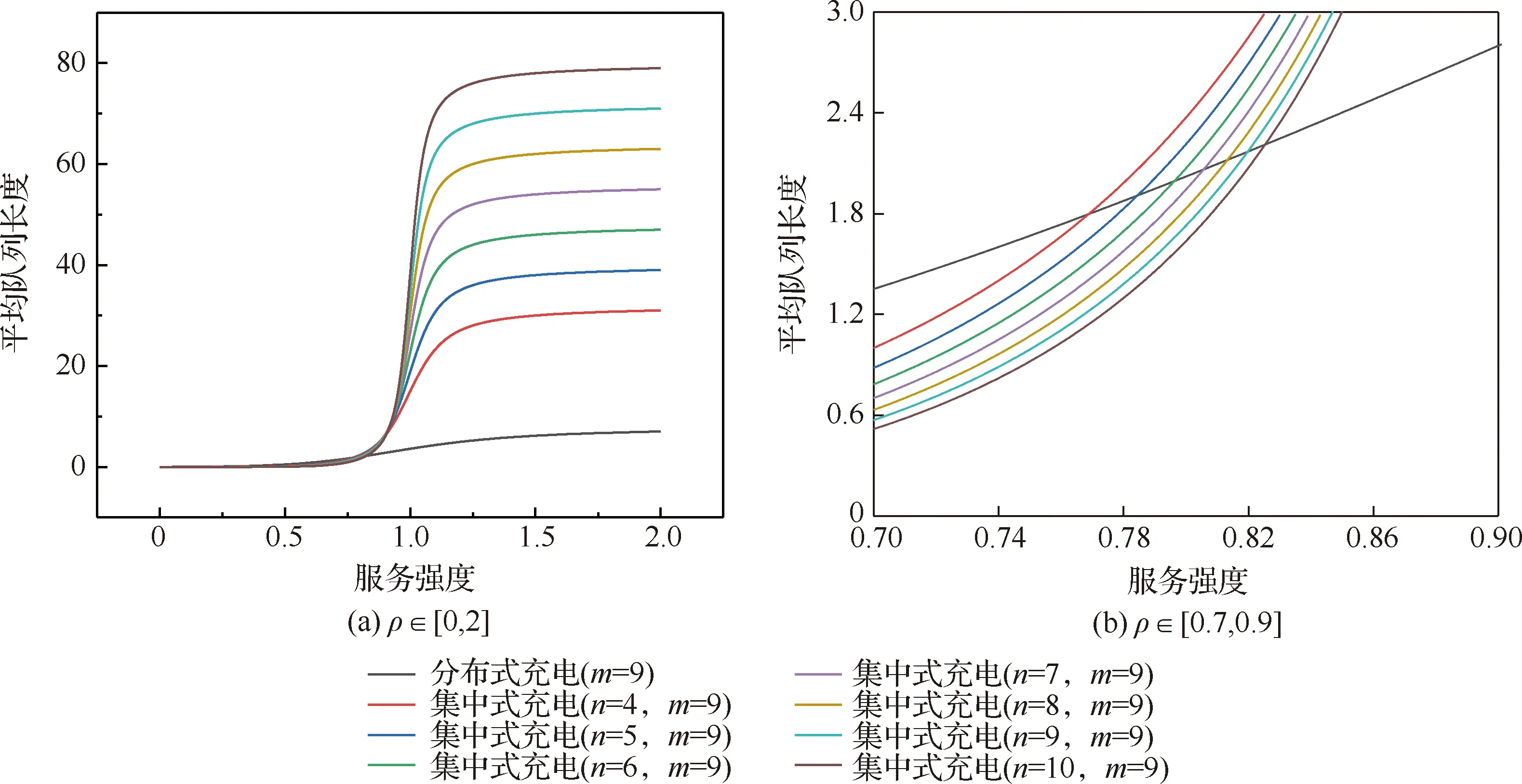
图9 系统容量为9时的平均队列长度对比Fig.9 Comparison of average queuing length when system capacity is 9

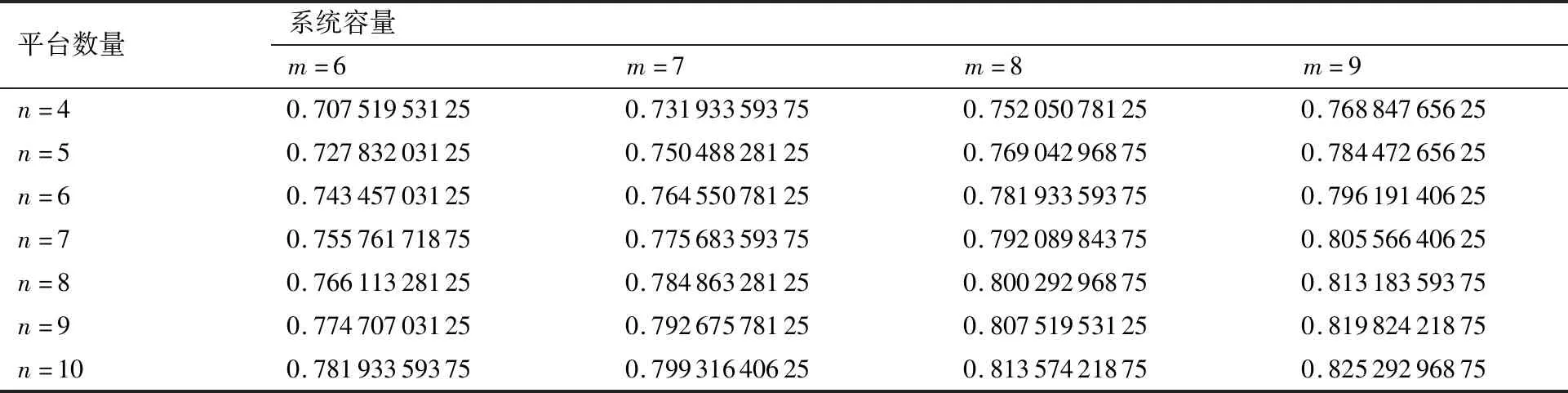
表2 2种充电方式平均队列长度曲线的交叉点Table 2 Intersection of average queuing length curves of two charging methods

4.2 平均等待时间

观察3.1节的式(12)和3.2节的式(14)，其中均有共同的因子λ的倒数。将其消去后，如式(18)和式(19)所示。因此，可以通过计算td和tc之间的大小关系，实现对2种充电方式的比较。

(18)

(19)

与4.1节处理方法一致，首先将系统容量设定为6。绘制2种充电方式的平均等待时间，即td和tc随服务强度及平台数量变化的曲线图，如图10所示。

依据图10可以发现，在服务强度的区间为[0,2]时，随着服务强度的增长，2种充电方式的平均等待时间随之增长。服务强度较小时，集中式充电的平均等待时间低于另一者。但两者在服务强度为1附近产生交叉点，在这一交叉点后，集中式充电的平均等待时间会高于另一者。

图10 系统容量为6时的平均等待时间对比Fig.10 Comparison of average waiting time when system capacity is 6

从图11～图13中可以看到，随着服务强度的增加，与4.1节类似。服务强度较低时，若以平均等待时间作为评判指标，集中式充电比较有优势。但随着服务强度的增加，分布式充电的优势逐渐体现。通过数值分析中的二分法，取区间为(1.000 1,1.125)，精度为0.000 1，可以求解出每一个交叉点的横坐标，如表3所示。

图11 系统容量为7时的平均等待时间对比Fig.11 Comparison of average waiting time when system capacity is 7

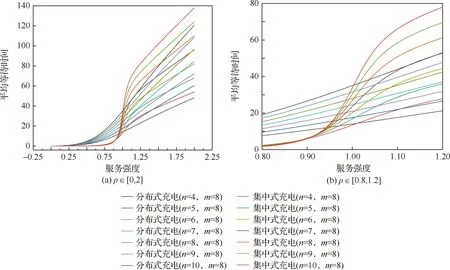
图12 系统容量为8时的平均等待时间对比Fig.12 Comparison of average waiting time when system capacity is 8

表3 2种充电方式平均等待时间曲线的交叉点Table 3 Intersection of average waiting time curves of two charging methods

5 结 论

1) 在服务强度的区间为[0,2]时，随着服务强度的增强，评价指标对应的曲线存在交叉点。交叉点前，即服务强度较低的情形下，集中式充电的两项评价指标优于分布式充电。但在交叉点后，随着服务强度的增大，分布式充电的两项评价指标优于集中式充电。

2) 对于不同充电平台数量和系统容量给出了选择集中式充电和分布式充电的交叉参考点，对蜂群无人机充电排队提供重要的参考。