压剪联合载荷作用下复合材料壁板屈曲及后屈曲性能计算与优化方法研究

李 政，梁 珂

(西北工业大学航空学院, 西安 710072)

0 引言

复合材料由于具有较好的比强度和比刚度，以及极度自由的可设计性，在航天航空结构工程领域得到广泛应用。目前飞行器结构设计不仅实现了复合材料使用比重的显著增加，其使用范围也逐渐从受力较小的构件向主承力结构进行转变。复合材料壁板是组成飞行器结构的重要承力构件，此类结构通常会受到轴压和剪切载荷的联合作用，容易在材料失效破坏之前发生屈曲失稳，造成结构承载性能下降[1-2]。故而，研究复合材料壁板的压剪承载性能，揭示铺层参数对壁板屈曲载荷和后屈曲承载性能的影响机理，对于提高复合材料在飞行器结构中的应用至关重要[3-5]。

即便采用当前先进的力学数值算法技术，针对复合材料壁板开展屈曲和后屈曲性能优化仍然存在种种困难[6]。首先，屈曲载荷和后屈曲性能分别由结构的面外和面内刚度水平控制，单独优化其中一个性能指标会引起另一个指标的明显下降；其次，计及几何非线性效应的结构屈曲分析计算量过大，常规非线性有限元方法已不适合用于优化迭代过程，不利于揭示屈曲及后屈曲优化的力学机理。早先，Pandey等[7]推导了计算复合材料受压板非线性屈曲性能的解析公式并用于铺层优化，发现单独优化后屈曲性能会明显降低屈曲载荷值。部分学者采用一种计算非线性屈曲响应的渐近数值方法(ANM)[8-11]来快速计算结构的屈曲及后屈曲响应。Raju等[12-13]成功将ANM方法用于轴压复合材料层合板的后屈曲优化；并基于变分原理和Rayleigh-Ritz方法，提出了一种用于复合材料层合板后屈曲分析的高效方法，采用层压参数作为设计变量，通过两步优化策略实现了后屈曲性能优化。

本文基于改进的Koiter摄动理论[14]，提出一种复合材料壁板在压剪联合载荷作用下非线性屈曲计算的有限元降阶方法，快速精确地获得结构屈曲及后屈曲性能指标，并将其用于壁板铺层优化，获得满足结构各类型性能设计要求的最优铺层设计。

1 复合材料壁板屈曲及后屈曲性能计算

采用常规的有限元离散化方法，复合材料壁板结构在压剪联合载荷作用下的非线性平衡方程可以用一组含N个未知数的非线性代数方程组f(q)=λfext来表示。其中，N是有限元离散模型的总自由度，矢量q表示结构位移场，向量f和fext分别表示结构内力和外力，荷载系数λ表示外荷载的加载变化。常规非线性有限元方法采用Newton-Raphson算法直接求解上述平衡方程，即可得到壁板的非线性承载响应，即q-λ曲线。

本文基于改进的Koiter摄动理论来构造上述有限元模型的降阶模型，该降阶模型在壁板的未变形状态处(q0,λ0)建立，用来近似非线性平衡方程。已知状态(q0,λ0)附近的未知构型(q,λ)可以用场变化量(u,μ)表示，即q=u+q0和λ=μ+λ0。为了简化平衡方程的非线性程度并求解场变化量(u,μ)，使用近似泰勒展开的方法将原先的平衡方程f(q)=λfext在已知构型(q0,λ0)处，关于位移变化量u展开至三阶项，即得

(1)

式中，二维张量L、三维张量Q和四维张量C分别是壁板内力在已知构型(q0,λ0)处的一次、二次和三次展开项。方程(1)的右端考虑了用于激发屈曲分叉变形的扰动载荷，使所提出的方法能够分析屈曲问题。在荷载矩阵F中，第一列向量f1=fext为外荷载，其他列向量fα，α=2,…,m+1表示各扰动荷载。扰动载荷是由壁板的密集屈曲模态和几何刚度的乘积计算获得，故而扰动载荷的数量m由壁板密集屈曲模态的数量决定。φ是载荷矩阵F中各载荷列向量系数所构成的载荷系数向量，其第一个分量为μ，其余分量均为0。

式(1)中的L，Q和C可以通过计算单元应变能相对于自由度的高阶导数来获得。本文采用基于Von Kármán运动学的四节点四边形复合材料板壳单元来实现有限元分析[14]。复合材料单元的内力f和切线刚度L可分别通过计算单元应变能的梯度和Hessian矩阵得到

(2)

NxKxx+NyKyy+NxyKxy)

(3)

式中，K0为单元的线弹性刚度矩阵，A表示单元面积，Cm为材料矩阵，Nx，Ny和Nxy表示单元内力矢量N的3个分量，Nnl为单元内力矢量N的非线性部分，Bl，Bnl，Kxx,Kyy,Kxy为单元的几何关系矩阵。

对复合材料铺层结构而言，其本构关系为

(4)

式中，N，M分别为单元的薄膜内力和内力弯矩，A和D分为是薄膜刚度和弯曲刚度。

继续计算单元应变能的三阶和四阶导数即可获得三维张量Q和四维张量C，然后将所有单元计算得到L，Q和C对整个结构进行组装，式(1)的显示表达即可获得。

仿照非线性平衡方程的展开方式，将位移和载荷系数向量u和φ基于摄动参数ξ进行展开可得

(5)

(6)

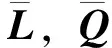
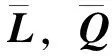
截断式(6)中的高阶项即可得到结构在未变形状态点处的降阶模型

(7)

上述降阶模型(7)本质上是一个具有(1+m)个未知数的非线性方程组，可以选择路径跟踪技术(例如弧长法)来求解该降阶模型，进而得到载荷系数μ与广义位移ξ之间的关系，然后再利用关系式λ=μ+λ0，q=u+q0和位移展开式(5)即可获得壁板非线性承载响应的非线性预测解(q-λ)。

受压/剪壁板面内位移随载荷的响应曲线呈现出典型的“双线性”曲线特征(图1)，即前屈曲阶段基本为线性承载，屈曲发生后曲线出现转折，后屈曲阶段出现明显的非线性特性。求解上述在未变形状态处建立的降阶模型，获得的非线性预测解能够准确跟踪壁板的前屈曲和初始后屈曲承载响应，壁板的屈曲和后屈曲性能指标可以通过分析该非线性预测解得到。本文所关心的3个指标，即非线性屈曲载荷、后屈曲承载刚度、承载刚度残余系数的具体计算方式如下：

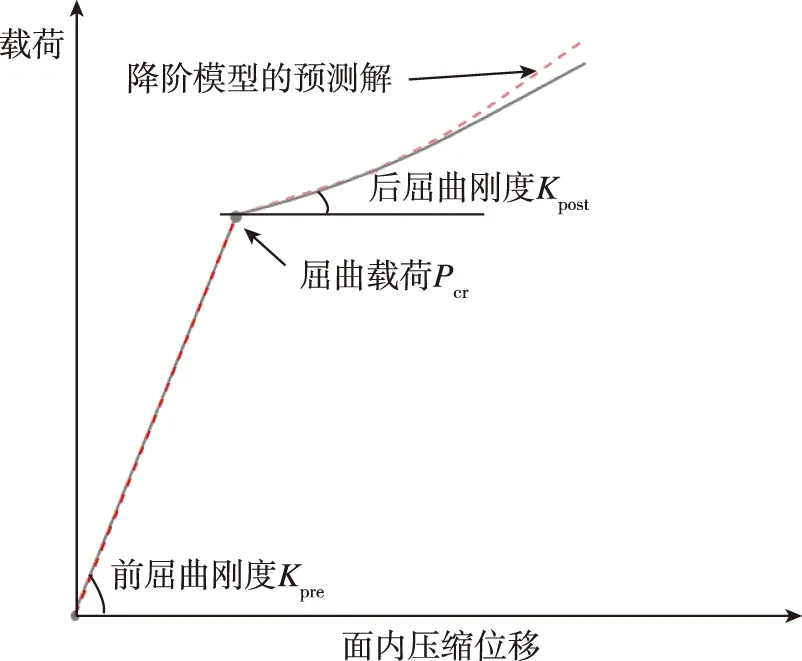
图1 压剪联合载荷作用下复合材料壁板的承载响应曲线Fig.1 The response for the composite panel under combined compression and shear loads

1)非线性屈曲载荷Pcr：该载荷值可通过探测壁板面内位移随载荷变化曲线的切线拐点获得。当非线性预测曲线在某载荷水平下的斜率值出现突变时，该载荷即为壁板的非线性屈曲载荷。

2)后屈曲承载刚度Kpost：该刚度为非线性预测曲线在屈曲载荷点处的斜率值。壁板后屈曲承载的非线性特性显著，用初始后屈曲刚度来表征壁板在后屈曲阶段的总体承载表现。

3)承载刚度残余系数kres：该系数值体现了壁板屈曲后承载刚度的折减情况。具体计算公式为kres=Kpost/Kpre，Kpre是壁板前屈曲阶段的承载刚度。Kres越接近1，表明壁板屈曲后承载能力损失的越小。

2 复合材料壁板屈曲及后屈曲性能优化

上一节提出了复合材料壁板在压剪联合载荷作用下屈曲和后屈曲承载性能计算的快速分析方法，即摄动有限元降阶法。本节的目标是将采用该方法计算得到的屈曲/后屈曲承载性能指标应用于壁板铺层优化，以找到复合材料壁板各种最优性能所对应的铺层方式θ。

在铺层性能优化中，复合材料壁板的总厚度设定为常数，各铺层的纤维铺向角度θi为离散整数设计变量，则屈曲及后屈曲性能优化问题设计如下

最大化：Pcr(θ)或Kpost(θ)或kres(θ)

设计变量：θ=[θ1,θ2,…,θi,…]

铺向角约束：-π/2≤θi≤π/2

性能约束(可选)：L.B.≤Pcr(θ)或Kpost(θ)或kres(θ)≤U.B.

上述优化问题中的性能约束需要依据实际设计要求来决定是否施加以及如何施加。

本文采用MATLAB优化工具箱来实现复合材料壁板的铺层优化，其所嵌套的遗传优化算法(GA)是一种成熟的优化方法，因此在下面的数值算例测试中采用了GA优化器所默认的参数设置，并用增广拉格朗日遗传算法(ALGA)和外部罚函数法求解非线性约束问题。使用摄动有限元降阶方法来计算壁板屈曲及后屈曲性能指标的速度非常快，因此本文采用获得全局最优解性能较佳的遗传类算法是一种合适的选择。

本文的算例考核工作采用计算机配置为8核的i7 CPU、16G内存，所提取的最优解均满足优化收敛条件，即GA优化算法自然停止并在窗口输出 “exitflag=1”的正常收敛信号，每个优化问题采用GA算法重复求解至少3次。

3 算例分析

受压剪联合载荷作用的复合材料壁板如图2所示，其长和宽分别为105 mm和75 mm，材料常数为E1=157 362 MPa，E2=10 092 MPa，G12=G13=5 321 MPa，G23=5 321 MPa， μ12=0.277， 复合材料铺层的单层厚度为0.125 mm。本算例采用14×10的复合材料四边形板单元来对壁板进性网格剖分。壁板采用四边简支的约束条件，即四条边均约束面外(z向)位移，右端约束面内轴向(x向)位移并在边中点处约束面内的另外一个方向(y向)位移。

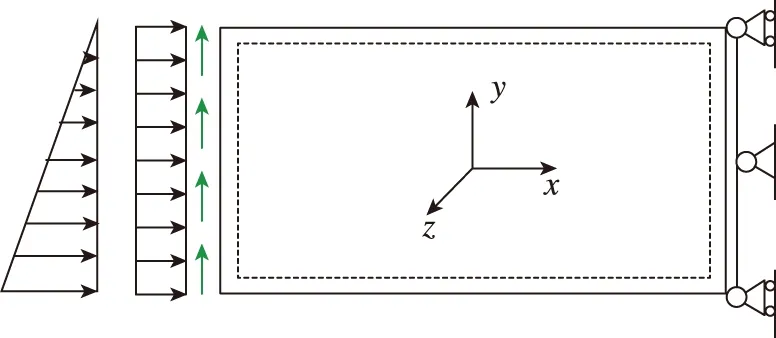
图2 压剪联合载荷作用下的复合材料壁板Fig.2 The composite panel under combined compression and shear loads

如表1和图2所示，壁板考虑两种不同的压剪复杂载荷条件：1)载荷工况1采用面内均匀压缩载荷和剪切载荷，压剪载荷的施加比例为1∶0.2；2)载荷工况2采用非均匀的压缩载荷和均匀剪切载荷。注意，两种载荷工况下，均匀压载和不均匀压载所施加的载荷总量相当。

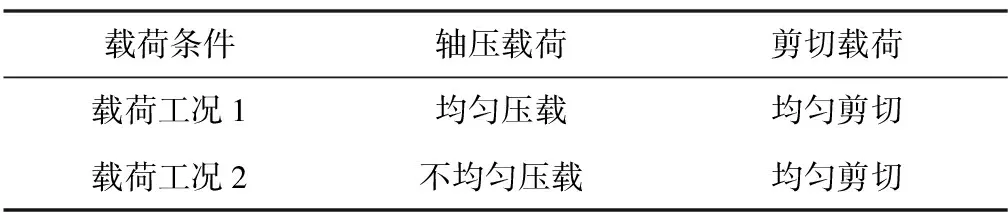
表1 两种载荷工况

3.1 壁板屈曲及后屈曲分析

先采用第2节提出的摄动有限元降阶方法分析某给定铺层方式的复合材料壁板。假设4铺层壁板的纤维方向为[15,30]s，按照载荷工况2施加不均匀面内压载和均匀剪切载荷。依照第2节中介绍的分析步骤，在未变形状态点处建立降阶模型时需基于壁板的前2阶密集屈曲模态，得到的降阶模型总自由度数为3。通过求解降阶模型可以获得壁板屈曲响应的非线性预测解，这里取面内压缩位移随加载变化曲线，如图3所示。图3中的两条响应曲线为分别采用基于常规非线性有限元方法和本文介绍的摄动有限元降阶方法计算获得，壁板在屈曲点处的变形也在图3中给出。可知，采用两种方法所获得的壁板承载响应曲线从未变形状态到初始后屈曲状态吻合得较好。两种方法计算获得的屈曲及后屈曲性能指标在表2中列出，两种方法计算出来的性能指标值也较为一致。在计算效率方面，采用本文的方法开展单次非线性屈曲计算的CPU时间在2 s以内，而采用常规非线性有限元方法则需要10 s 左右，计算效率显著提升。

图3 复合材料壁板非线性屈曲的承载响应曲线(载荷工况2)Fig.3 The nonlinear response for the composite panel

表2 两种方法计算的壁板屈曲/后屈曲性能指标比较

3.2 4铺层壁板屈曲及后屈曲性能铺层优化

针对4铺层壁板，采用对称铺设方式[θ1,θ2]s，铺层优化选取两个铺层的纤维角度θ1,θ2作为优化变量，在两种不同的载荷工况下暂不考虑性能约束，分别单独以非线性屈曲载荷、后屈曲承载刚度和承载刚度残余系数为优化目标开展铺层优化工作。优化计算得到的最优铺层信息及最优铺层对应的屈曲及后屈曲性能指标如表3～5所示。可以看出，单独优化后屈曲承载刚度会使屈曲载荷值显著下降，较最优屈曲载荷下降约50%。反之，最优屈曲载荷对应的后屈曲承载刚度仅为最优值的16%。面内压载荷的不均匀施加会使屈曲载荷的最优值下降约14%，但最优后屈曲刚度却稍有提高。可见，屈曲载荷值优化对面内压载荷的不均匀性更为敏感。总体来说，屈曲载荷值最优铺层的纤维铺向角集中在45°附近，后屈曲承载刚度值最优铺层的纤维铺向角集中在0°附近。经过优化的承载刚度残余系数能达到1附近，表明采用此类铺层的壁板在屈曲后基本没有承载刚度的损失。在计算效率方面，得益于本文提出的屈曲/后屈曲响应快速计算方法，单次优化计算仅约需要90 min左右。

表3 不同载荷工况下以非线性屈曲载荷值为目标的最优铺层信息

表4 在不同载荷工况下以后屈曲承载刚度值为目标的最优铺层信息

表5 不同载荷工况下以承载刚度残余系数值为目标的最优铺层信息

然后，以铺层[15,30]s作为优化前的参考铺层，将载荷工况2下参考铺层和各性能最优铺层发生屈曲时的变形图绘制在图4中。最后，在后屈曲承载刚度的优化过程中引入屈曲载荷约束，即Pcr>250 N，得到的最优铺层如表6所示。可以看到，当引入屈曲载荷约束后，获得的最优解均满足约束要求，可以得到满足一定抗屈曲性能的最优后屈曲承载刚度铺层结构，该铺层的两个纤维角度变量分别在45°和0°附近。

表6 不同载荷工况下以后屈曲承载刚度值为目标的最优铺层信息-考虑屈曲载荷约束

图4 4铺层壁板各性能指标最优铺层在屈曲点处的变形图(载荷工况2)Fig.4 The deformation of the optimal 4-ply panel at the buckling point for different performance index under the second load condition

3.3 16铺层壁板屈曲及后屈曲性能铺层优化

针对16铺层壁板同样采取对称铺层方式[θ1,θ2,θ3,θ4,θ5,θ6,θ7,θ8]s,铺层优化选取θ1,θ2,θ3,θ4,θ5,θ6,θ7,θ8作为优化变量进一步丰富了优化空间，在两种载荷工况下分别以非线性屈曲载荷、后屈曲承载刚度和承载刚度残余系数作为优化目标进行优化任务。优化计算得到的优化纤维铺层信息以及对应的屈曲和后屈曲性能指标如表7～8所示。以屈曲载荷为优化目标的计算会引起后屈曲刚度大幅下降，相较于最优后屈曲刚度下降了85%。最优后屈曲刚度对应铺层的屈曲载荷与最优屈曲载荷相比下降了64%。该部分结果与4铺层结果对照发现，改变壁板厚度并不能缓解屈曲载荷和后屈曲刚度的矛盾。比较两种工况下的优化结果，不均匀载荷对屈曲载荷仍有10%的影响，但是对后屈曲刚度的影响已经变得很小。最优屈曲载荷对应的铺层集中在45°左右，最优后屈曲刚度对应的铺层集中在0°左右，最优承载刚度残余系数对应的铺层内层角度较大而外层角度较小。虽然可行解数量增加为原来的1806倍，但是单次优化计算用时仍在10～20 h范围内。载荷工况1下的各优化铺层发生屈曲时的变形图如图5所示。

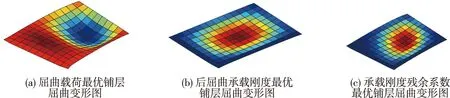
图5 16铺层壁板各性能指标最优铺层在屈曲点处的变形图(载荷工况1)Fig.5 The deformation of the optimal 16-ply panel at the buckling point for different performance index under the first load condition

表7 不同载荷工况下以非线性屈曲载荷值为目标的最优铺层信息

表8 不同载荷工况下以后屈曲承载刚度值为目标的最优铺层信息

表9 不同载荷工况下以承载刚度残余系数值为目标的最优铺层信息

4 结论

本文针对压剪联合载荷作用下的复合材料壁板，采用非线性摄动有限元降阶方法高效精准地计算了壁板的屈曲和后屈曲性能指标，并将其成功嵌套在铺层性能优化流程，获得满足性能设计要求的最优铺层信息,得出以下结论：

1)与传统非线性有限元方法比较，本文采用摄动有限元降阶方法所获得的壁板承载响应曲线从未变形状态到初始后屈曲状态吻合得较好，计算获得的屈曲及后屈曲性能指标精度较高，单次非线性屈曲计算的CPU时间在2 s以内，计算效率提升约80%。

2)单独优化后屈曲承载刚度会使屈曲载荷值显著下降，反之亦然。屈曲载荷值优化对面内压载荷的不均匀性更为敏感。屈曲载荷值最优铺层的纤维铺向角集中在45°附近，后屈曲承载刚度值最优铺层的纤维铺向角集中在0°附近。经过优化的承载刚度残余系数能达到1附近，表明采用此类铺层的壁板在屈曲后基本没有承载刚度的损失。

3)在后屈曲承载刚度优化中引入屈曲载荷约束后，可以得到满足一定抗屈曲性能要求的最优后屈曲承载刚度铺层结构，该铺层的两个纤维角度变量分别在45°和0°附近。