APOS理论视角下的初中数学概念教学

吴洁瑜

【摘 要】 APOS理论旨在数学概念教学中使学生建立起适当的心理结构，与其他相关概念形成综合图式。本文主要从“活动”“过程”“对象”“图式”四个阶段，以“黄金分割”为例，分析和探讨APOS理论在初中数学概念教学中的应用。

【关键词】 APOS理论;初中数学;概念教学;黄金分割

一、APOS理论概述

APOS理论最开始是美国著名数学教育家杜宾斯基提出的，他认为学生学习数学概念就是要建构心理结构。数学概念的学习不仅可以建立在具体存在的对象上，也可以建立在学生已有的认知基础和能力水平上，将新概念与旧知融合，从而建构更高层次的心理结构。这一建构的基本模型经历4个阶段：A——Action（活动）、P——Process（过程）、O——Object（对象）、S——Schema（图式）。该理论认为学生在数学学习过程中若经过了前三个阶段，一般就能够在思考、建构的基础上形成综合心理图式，进而将问题顺利解决。

杜宾斯基还认为，活动、过程、对象也可看作是数学知识的三种状态，而图式则是由这三种知识构成的一种认知结构。虽然这四者具有先后顺序，但实际上学生对某一数学概念的理解并不只是线性的，还可以是循环的。

新课标一直倡导，学生是课堂活动的主体，而教师则是活动的组织者、引导者和合作者。学生学习应该是一个生动活泼的、主动的和富有个性的过程。这和APOS学习理论是一致的。在初中数学的概念教学中，也应该做到让学生在做中学，将抽象的概念内化到学生原有的认知结构中，而不是由教师将抽象概念灌输给学生。根据笔者近四年的初中数学实际教学经验，认为有必要将APOS学习理论应用于初中数学的概念教学，现结合九年级下“黄金分割”一课谈谈APOS理论在初中数学概念教学中的应用。

二、概念教学

1.概念的引入——活动（Action）阶段

这里的活动是指学生通过教师预先设置的问题进行外部刺激，一步一步地通过引导性指令去感受一个客观的数学对象。数学课堂教学其实是数学活动的教学，经历一系列的操作活动是学生数学认知的基础性行为。学生可以感受数学家探索实验发现的整个过程，通过动手实践来获得经验、概念。其实，数学活动的实验过程除了像生物、化学等学科中的观察实验以外，还需要合情推理、演绎推理、运算实验。没有行为操作和心理操作，数学概念也就没有了心脏，而教师则要扮演好课堂活动的组织者、引导者和合作者的身份。

例如，笔者在“黄金分割”概念教学中，先是给出一组照片（如图3），让学生感受哪一张图片第一眼的视覺效果更好看，学生基本上都会认为中间一张更好看。这一环节的设置从外部刺激学生探究新知概念的兴趣。也就是为什么大家都会有这种视觉的感受。紧接着将照片对象抽象为线段上的点（如图4），引导学生探究为什么照片对象在这样的位置会看起来更好看。学生开始尝试用“度量”的方法得到线段AB、BC和AC的长度，教师引导：这三条线段之间有什么样的数量关系或比例关系？学生通过计算，得出≈0.618的黄金比。教师再引导：0.618具体是什么数？假设线段AC为单位1，会得出什么结论？学生尝试利用方程思想，设BC=x，由得到，解得。整个概念引入过程让学生从操作、运算等实践活动中感受数学家的认知过程，使学生深入地理解黄金分割点和黄金比概念的由来，而不单单是0.618或者是等生硬的数字。

2.概念的归纳——过程（Process）阶段

经过活动的不断重复，行为操作就可以内化为一种叫作“过程（process）”的心理操作，但活动不是数学教学的目的，一节课就40分钟，如果放任活动，教学效果也不会理想。因此就需要教师的引导者作用，引导学生对“活动”进行思考，经过思维的内化，从而归纳出特定概念所特有的性质。学生一旦经历了这一“过程”，就有了之前活动的经验和思维，不需要再通过外部指令的刺激也能获得概念。也就是说，学生有了活动阶段形成的经验和思维并可以自然地应用，甚至还能够将这些经验和思维重新排列和组合，形成新的经验思维。

例如，学生在第一环节归纳出了黄金分割点和黄金比的概念，而不必再进行具体的运算，并且能从单位1延伸到n的表达，也就是说，当已知点B是线段AC的黄金分割点（AB>BC），当AC=n，学生就能得到AB≈0.618n，那么他就已经完成了这种“过程”模式的建构，接下来教师可以继续引导：“一条线段有几个黄金分割点？”在这一阶段，教师可以借助信息技术和多媒体手段辅助教学，这样能更好地展示概念的内涵和外延。

3.概念的巩固——对象（Object）阶段

当学生能把内化概念的“过程”进行新一轮的实践和转化的时候，这一“过程”就转化为学生心理内部的一种独立“对象”，也就是学生通过前面的活动了解到了概念的形成过程，并对概念给出了具体的定义、数学符号以及数学语言，使得概念更加具体和精致，并压缩为一个具体的对象。这个“对象”的过程也就是对数学概念的内涵和外延进行进一步加工，使学生更新和建构新的心理结构，建立更清晰的概念表象。概念进入“对象”阶段时，建构的结构关系也就相对稳定。

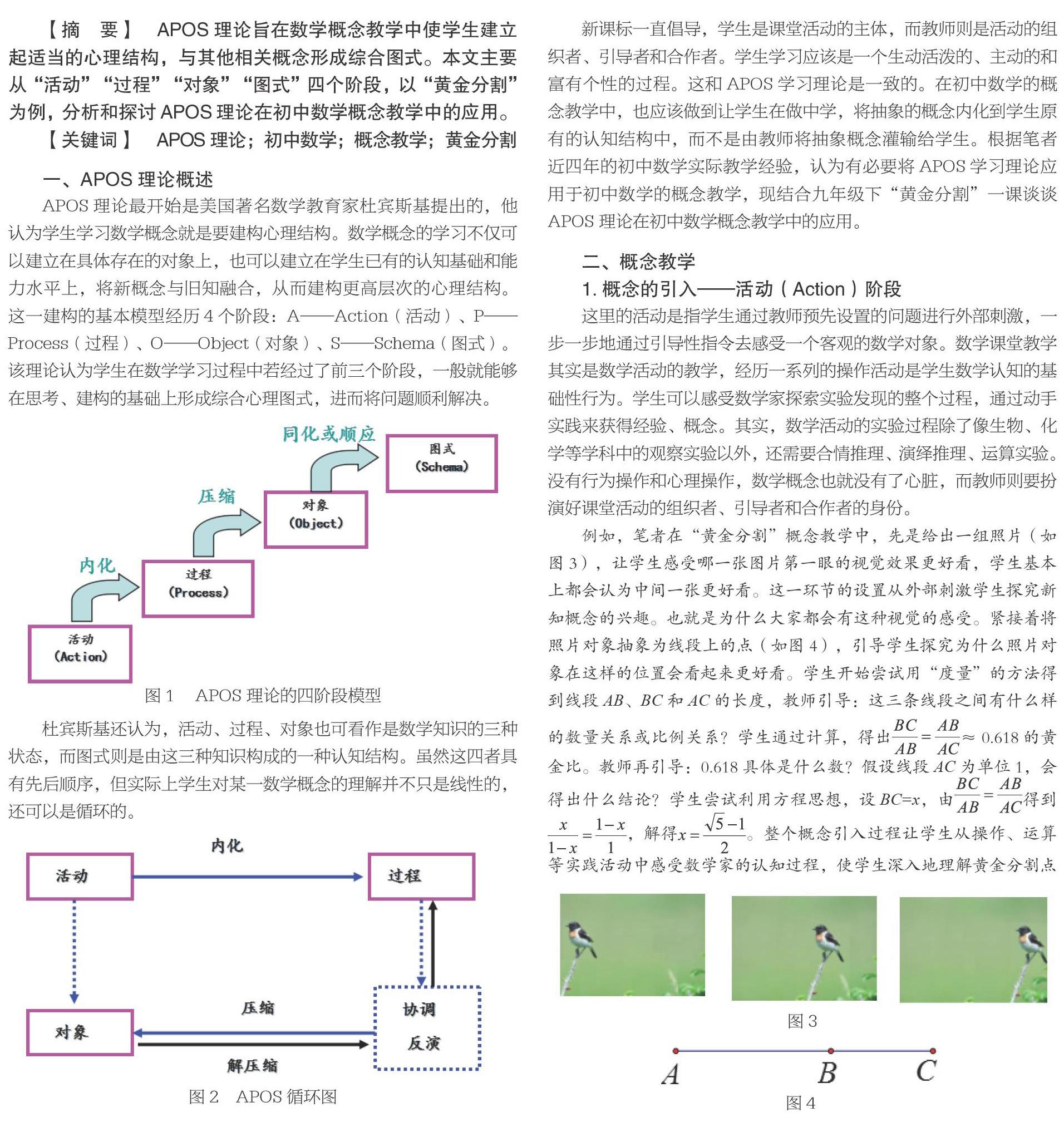
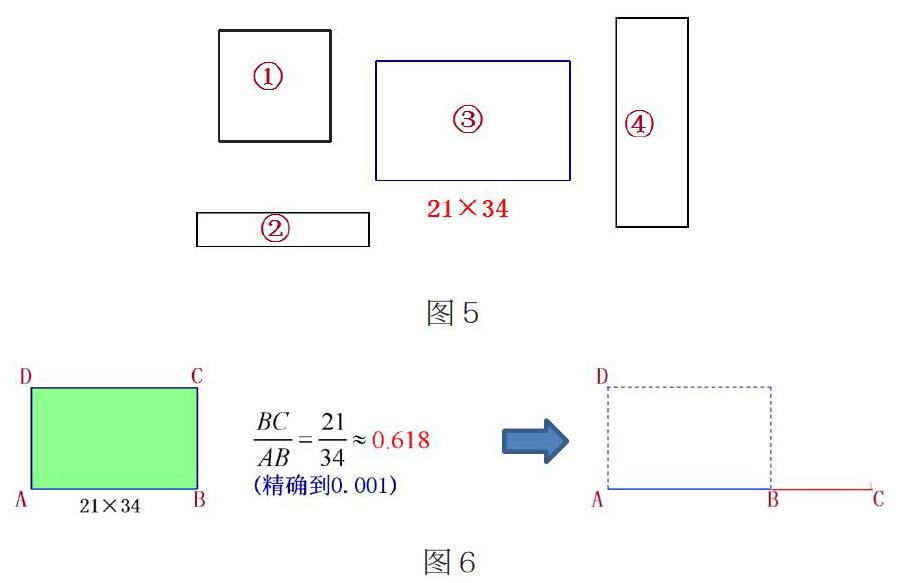
这一阶段，教师可以设计2～3个生活中的实际问题，让学生在解决问题的过程中巩固概念，同时，教师注重剖析表达式中精炼的数学语言和符号所表示的含义，让学生在解决问题的过程中分析概念所适用的条件和范围。“对象”既是概括的结果，又是新的概括的起点。例如，在“黄金分割”一课中，笔者在问题解决的过程中又提出了一个新的问题：如图5，下面的矩形中哪一个更好看？大部分同学都会选择③号矩形。此时再次引导学生探究：为什么这样的矩形更好看？这个矩形的宽和长的比有什么特点？学生会在前面建立的思维引导下，通过计算发现宽与长的比值就是黄金比。在这一过程中，笔者利用多媒体动态演示，将矩形的宽BC绕着点B顺时针旋转90°，使得BC与长AB共线，让学生更加直观地感受到点B为线段AC的黄金分割点，如图6。

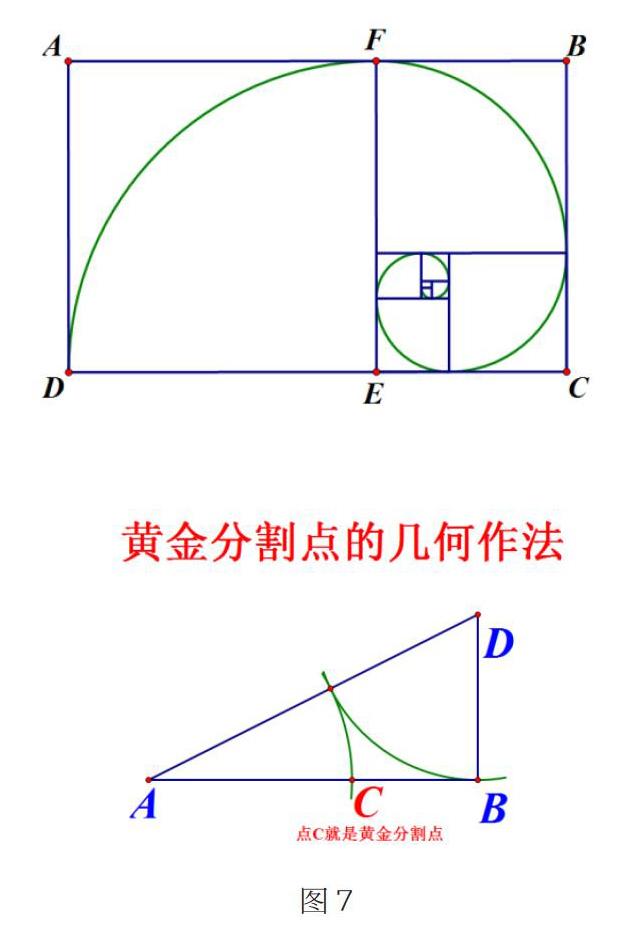
这一环节建立在学生已有的“黄金分割点”和“黄金比”的概念基础上，又继续探索研究生成的“黄金矩形”的概念。再次活动探究，笔者又通过几何画板演示黄金曲线的生成过程，帮助学生内化黄金矩形与黄金曲线概念的生成以及概念与概念之间的内在联系。 在这个基础上，笔者引导学生对黄金分割点进行尺规作图，并让学生探讨此种做法的科学性（如图7）。通过新一轮的内化、压缩、解压如此循环之后，学生最终形成完整的黄金分割概念这一“对象”。

4.概念的模型生成——图式（Schema）阶段

数学概念的“图式”阶段是经历了“活动”“过程”“对象”包括已有的数学概念，和其他“图式”一起进行新的排列组合所形成的一种认知结构。那么经过上述三个阶段的上升学习过程，学生已经形成了关于黄金分割的概念，并且会更新和构建新的认知结构，它可用于解决与这个概念相关的问题。那么黄金分割在实际生活中有哪些运用？此时可以布置作业，让学生利用书籍和网络搜集有关黄金分割在建筑、音乐、美术、体育、生物等各个领域中运用的实例，再进行一次班级分享交流，使学生建立黄金分割与其他相关概念的综合图式。

APOS理论认为概念的生成来源于学习者的反复操作和不断反思，从而形成静态结构，也就是对象阶段。初中阶段的数学概念基本都涉及操作（活动）、对象和过程，需要教师进行组织、引导和协调，帮助学生构建一个又一个连贯的概念框架，也就是APOS理论中所说的综合图式，这种图式可以帮助学生在解决数学问题的时候灵活运用所需的数学思维，提高学生自主学习、动手实践、合作探索和解决问题的能力，同时也对教师的综合素养提出了更高的要求。

【参考文献】

[1]曾玉祥.APOS理论在高等数学概念探究式教学中的应用[J].教育探索，2013（5）：42-43.

[2]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.