注重模型思想解决数学问题——以《积相等（二）》一课为例

汤雷萍

模型思想是《数学课程标准（2011年版）》中十个核心词之一，是学生体会和理解数学与外部世界联系的基本途径。在教学中怎样让学生经历模型思想的建立过程？怎样让学生学会用模型思想解决现实生活或具体情境中抽象出的数学问题？这是这节课需要思考的核心问题。因此在教学设计中紧紧围绕模型思想创设教学环节，将常见的工程问题、单价问题、速度问题紧紧与几何模型相关联，引导学生寻找具体情境中的数量关系，并通过与几何模型建立联系，体会并逐步建立模型思想。

【教学过程】

一、借助几何图形找模型

师：（出示1个正方形）老师变个魔术，（变成2个正方形）它们的大小是一样的。现在我把①号正方形平均分成3份，②号正方形平均分成4份，你能根据图写出一个等量关系式吗？

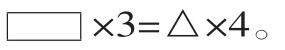
师：你们能看懂这个等量关系式吗？谁能来解释一下？

生：长方形乘3就是①号正方形，三角形乘4就是②号正方形，①号和②号是相等的，所以这个等式成立。

师：假如①号正方形中1个长方形表示8，则②号正方形中1个三角形表示多少？

生：先算出①号正方形，3×8=24，②号正方形和①号正方形一样大，所以24÷4=6。（板书：3×8=24，24÷4=6）

师：利用刚才的等量关系，老师这样写能理解吗？

（板书：8×3=△×4）

生：可以。1个△=8×3÷4=6。

【设计意图：本节课的重点是让学生能借助几何图形来建立积相等的数学模型，理解积相等关系，进而解决生活中的一类数学问题。教学先让学生从两个相等的正方形中寻找等量关系，写出积相等的式子，再有意识地利用积相等关系去解决相应的数学问题。几何直观是解决问题强有力的工具之一，从几何图形的关系中引入，为学生解决问题提供表象和方法的支撑。】

二、探究问题，进一步建立模型思想

1.合作学习。

师：这节课我们继续用积相等的知识来解决生活中的数学问题，请看问题，根据题目意思写出等量关系式，再列式解答。

（1）出示题目：加工一批零件，师傅每天加工28个，3天可以完成。如果让徒弟单独加工需要4天才能完成，徒弟每天加工多少个零件？

（2）集中反馈学生的作业。

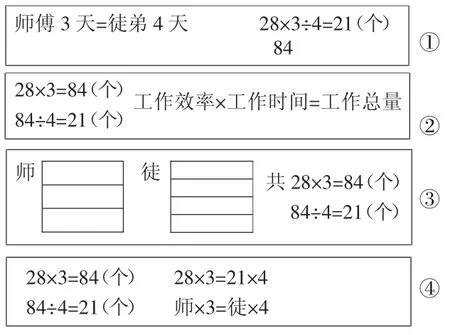
师：请先观察这几个等式，你同意吗？你认为最能体现题目意思的是哪些等量关系式？

生：我不同意第②种方法，虽然这个数量关系公式是对的，但是没有最佳体现题目意思，这也不是一个等量关系式。

生：我同意第③种方法，他用图表示出了师傅3天做的总量=徒弟4天做的总量。

生：我同意第①种方法，师傅3天做的就等于徒弟4天做的，和第③种方法一样。

生：我认为第④种方法也很好，和第①种方法意思相同。

师：也就是说，其实方法①③④要表达的意思是一样的，那选一个关系式的话，我们选——

生：第④种方法，积相等的关系式。

【设计意图：让学生在具体情境中寻找并表征等量关系，在比较中得出积相等关系式，逐步渗透模型思想。】

师：（板书：师傅每天加工的×3天=徒弟每天加工的×4天）这又是一个积相等的关系式。请观察，与刚才图形中得到的积相等关系式比较，有什么联系？

生：师傅每天加工的就相当于①号正方形中的1份，3天就是3份，而徒弟每天加工的则是②号正方形中的1份，4天就是4份。他们加工的总量是相等的。

生：（指着黑板板书说）①号正方形中的1个长方形就相当于师傅每天加工的28个，3个长方形就是3天；②号正方形中的1个三角形就相当于徒弟每天加工的数量，4个三角形就是4天，师傅和徒弟的总量是相等的。

【设计意图：结合具体情境问题，把等量关系式与几何图形中的等量关系式进行对比，寻求关联，沟通代数表达式和几何模型，丰富学生对积相等的关系理解，并积累数量关系分析的经验和工具，有利于促进学生对数量关系的概括和推理。】

2.自主学习。

师：积相等的知识可以解决很多问题。先补充问题，再写出等量关系式，最后解决问题。

出示：一笔钱可以买单价50元的A商品12件，B商品单价是60元，__________？

生：我找到等量关系式是：A商品单价×12件=B商品单价×（），它们的总价相等。所以先求总价，再除以单价就等于数量。

师：我们又得到了一个新的等量关系式，［板书：A商品单价×12件=B商品单价×（数量）］那么这个等量关系式跟刚才的几何图形中的等量关系有联系吗？

【设计意图：学会学习就是学会迁移与应用。基于之前学习中掌握的知识和积累的经验，学生能比较容易地补充所求的问题，并且顺利写出数量关系的等式。学生能正确地补充问题，说明已掌握数量之间的积相等关系，能够在水平变化的情境中进行识别和应用。】

三、拓展练习，巩固模型思想

1.自主编题：从杭州东站到上海虹桥机场，小汽车的速度是84千米/时，中巴车的速度是56千米/时，小汽车需要行驶2小时，中巴车需要行驶3小时。

学习要求：（1）根据提供的信息，把其中一个信息变成问题，编一道题目。（2）先写等量关系，再解答。

2.寻求联系：结合几何图形，说说有什么联系？

【设计意图：自主编题对数量关系的分析要求进一步提高，特别地，在不同的问题情境中讲述相同数量关系的故事，需要一定的抽象能力。让学生根据速度×时间=路程这个数量关系，路程一定，则可以得出“小汽车速度×2小时=中巴车速度×3小时”这个等量关系式，只要已知其中三个信息，则可以求出另一个信息。把讲述不同故事的应用问题与几何图形建立联系，充分利用几何直观理解数学模型。】

3.结合板书，回顾：有人说，今天我们做了四道题目，有人说，其实我们只做了一道题。对此，你能说说自己的想法吗？

（学生观察思考后很快发现工程问题、单价问题和路程问题这三道题都可以和几何图形题联系起来，都用了积相等的知识）

【设计意图：归纳、概括出一类问题的统一模型，突显积相等的模型，强化学生的模型思想。几何直观在模型思想的建立中发挥了独特的作用。】